双分数跳-扩散过程下篮子期权定价

淡静怡,　薛　红

(西安工程大学 理学院，陕西 西安　710048)



双分数跳-扩散过程下篮子期权定价

淡静怡,薛红

(西安工程大学 理学院，陕西 西安710048)

期权定价是金融数学的核心问题之一,金融资产价格的变化过程是期权定价理论的基础。传统的期权定价模型是假定资产价格服从几何布朗运动,而双分数布朗运动是一种更为一般的高斯过程,并且增量不具有平稳性,可以描述更多的随机现象。文章采用双分数布朗运动描述资产价格变化过程比传统模型更具优越性,假定股票价格服从双分数跳-扩散过程,借助双分数布朗运动和跳-扩散过程随机分析理论,利用保险精算方法研究篮子期权定价问题,得到双分数跳-扩散环境下欧式几何篮子期权定价公式。研究结果对篮子期权定价模型进行了推广,使之更适用于实际的金融市场。

双分数布朗运动;跳-扩散过程;保险精算方法;几何篮子期权

0　引　　言

期权定价问题是金融数学的核心问题之一,随着金融市场的不断发展,近年来市场上出现了许多新型期权, 篮子期权就是新型期权的一种。 篮子期权是一种多资产期权, 其收益是由多个标的资产的加权平均价格决定的, 欧式篮子期权的加权平均价格可分为几何平均和算数平均, 本文主要讨论欧式几何平均篮子期权定价问题。文献[1]利用风险中性方法给出了布朗运动环境下欧式几何篮子期权定价公式;文献[2]利用偏微分方程方法, 得到了布朗运动环境下欧式几何篮子期权定价公式;文献[3]利用保险精算法讨论了分数布朗运动环境下欧式篮子期权定价公式。在实际金融市场中股票价格可能会出现“跳跃”，文献[4]在跳-扩散模型下,利用条件期望和矩法得到篮子期权的价格;文献[5]利用风险中性定价原理得到了跳-扩散过程下的篮子期权定价;文献[6]首次提出了双分数布朗运动这一概念, 它是一种比分数布朗运动更一般的自相似高斯过程,经过长期的研究与实证对比发现,用双分数布朗运动驱动的随机微分方程来刻画资产的价格变化更加符合实际的需求, 关于双分数布朗运动在金融市场中的应用可参见文献[7-8]。目前关于期权定价的方法很多, 如鞅方法、偏微分方程方法和保险精算方法等, 其中保险精算方法适用的范围更加广泛,它不仅适用于完备的、无套利的、均衡的金融市场,而且也适用于不完备的、有套利的、非均衡的金融市场,其主要思想是将期权定价问题转化为公平保费问题, 关于保险精算方法在金融市场中的应用可参见文献[9-11]。

目前国内外对双分数布朗运动环境下的各种期权定价的研究还比较少, 本文在双分数布朗运动环境下,建立更贴合市场的金融数学模型,对跳-扩散过程下篮子期权定价公式进行了研究,使之能更好地应用到金融市场中去,并在此基础上进行了相应的推广。

1　数学模型

s,t≥0,

其中,H∈(0,1)；K∈(0,1]。

当K=1时,双分数布朗运动退化为分数布朗运动,当K=1,H=1/2时,双分数布朗运动退化为标准布朗运动。有关双分数布朗运动的相关理论可参见文献[6-8]。

假设股票价格{Si(t),t≥0}满足微分方程：

(1)

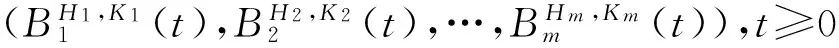
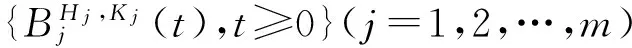
引理1随机微分方程(1)的解为:

(2)

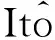
假定在t1∈[0,t]时刻内只发生1次跳跃,则在时刻[0,t1)内有:

在(t1,t]时刻内有:

(3)

由(1)式有:

当n→+∞时,可得:

即

将Si(t1)代入(3)式可得:

因此当跳跃的次数服从泊松过程时,可得:

从而引理1得证。

定义2过程{Si(t),t≥0}在区间[t，T]上的期望回报率βi(u),u∈[t,T]定义[13]为:

引理2股票价格{Si(T),T≥0}在[t,T]上的期望回报率βi(u),u∈[t,T]为:

(4)

证明因为

所以

又由{Uij,j=0,1,2,…}独立同分布可知:

从而可知E[Si(T)]=Si(t)exp{μi(T-t)},所以有:

从而引理2得证。

在实际中,预期收益率μi是投资者认为会有的报酬率,期望回报率βi是实际回报的期望。如果存在红利等其他因素时,期望回报率与预期收益率两者是不相等的,而本文不涉及红利等因素,因此为了表明两者关系,本文提出引理2并给出了证明。

2　篮子期权定价公式

欧式几何篮子看涨期权的损益函数[2]为:

(5)

其中,T为到期日;X为执行价格;αi为第i个股票在几何篮子期权中所占的比例,且

定义3欧式几何看涨篮子期权在0时刻的保险精算价格定义为:

(6)

定理1欧式几何看涨篮子期权在0时刻的保险精算价格为:

Cn=exp{d-rT+lnX}×

(7)

其中,Φ(x)为标准正态分布函数；

ki(i=1,2,…,n)表示第i个股票在区间[0,T]上跳跃的次数。

证明记

由引理1与引理2知A={η>-d},根据定义3可知:

(8)

由全期望公式可得:

(9)

其中,

因为ξ～N(a,b), 所以有:

(10)

由(9)式、(10)式可得:

(11)

因为

(12)

所以将(11)式和(12)式代入(8)式可得结果。

综上所述，当n=1时,可得双分数跳-扩散下欧式期权定价公式,具体参见文献[8]；当λi=0时,可得双分数布朗运动环境下的篮子期权定价公式；特别地,当K=1时,可得分数布朗运动环境下篮子期权定价公式,具体参见文献[3]。

3　结　论

篮子期权由于它价格上的优势与其本身所具有的灵活性使人们对其需求越来越大,因此对篮子期权进行研究有很大的实际意义,而为了让篮子期权能更好地应用于实际的金融市场,本文在传统模型的基础上,采用双分数布朗运动去刻画金融市场的资产价格,利用跳-扩散过程随机分析理论与保险精算方法,讨论双分数跳-扩散过程下的几何篮子期权定价问题,并对分数布朗运动环境下的篮子期权定价的相关结论进行了推广,使其更具有实际意义。

[1]陈松男.金融工程学[M].上海:复旦大学出版社,2002:78-84.

[2]姜礼尚.期权定价的数学模型和方法[M].北京:高等教育出版社,2003:216-218.

[3]党柳梦,薛红,卢俊香.分数布朗运动环境下欧式篮子期权定价[J].哈尔滨商业大学学报(自然科学版),2013,29(5):598-599，613.

[4]XU Guoping,ZHENG Harry.Approximate basket options valuation for a jump-diffusion model[J].Insurance:Mathematics and Economics,2009,45(2):188-194.

[5]柯开明,王建华，王玉玲.美式-篮子期权定价的蒙特卡罗模拟改进技术[J].统计与决策,2004(9):19-20.

[7]肖玮麟,张卫国,徐维东.双分式布朗运动下股本权证的定价[J].系统工程学报,2013,28(3):348-354.

[8]XUE H,WU J Z.Pricing european option under bi-fractional jump-diffusion process[C]//The 2015 3rd International Conference on Advanced Information and Communication Technology for Education.Guangzhou:Atlantis Press,2015:267-270.

[9]郑红,郭亚军,李勇,等.保险精算方法在期权定价模型中的应用[J].东北大学学报(自然科学版),2008,29(3):429-432.

[10]闫海峰,刘三阳.广义Black-Scholes模型期权定价新方法:保险精算方法[J].应用数学和力学,2003,24(7):730-738.

[11]张学莲,薛红.股票价格遵循分数-跳扩散过程的期权定价[J].纺织高校基础科学学报,2008,21(4):446-450.

[12]RUSSO F,TUDOR C A.On the bifractional brownian motion[J].Stochastic Processes and Applications,2006,116(5):830-856.

[13]毕学慧,杜雪樵.后定选择权的保险精算定价[J].合肥工业大学学报(自然科学版),2007,30(5):650-651.

(责任编辑张镅)

Basket option pricing under bi-fractional jump-diffusion process

DAN Jingyi，XUE Hong

(School of Science, Xi’an Polytechnic University, Xi’an 710048, China)

Option pricing is one of the core problems of financial mathematics, and the price process of financial underlying asset is the basis of option pricing theory. In the traditional option pricing mode, it is assumed that asset price follows geometric Brownian motion, but the bi-fractional Brownian motion is a more general Gaussian process, and does not have stationary increments, which can describe more random phenomenon. Bi-fractional Brownian motion has more advantages than the traditional model in describing the asset price process. Assuming that stock price satisfies the bi-fractional jump-diffusion process, and using the stochastic analysis theory for bi-fractional Brownian motion and jump-diffusion process, the pricing problem for European geometric basket option is discussed by using the insurance actuary approach, and the pricing formula of European geometric basket option in bi-fractional jump-diffusion environment is obtained. The result of basket option pricing model is generalized, and it is more applicable to actual financial market.

bi-fractional Brownian motion; jump-diffusion process; insurance actuary approach; geometric basket option

2015-12-15；

2016-05-04

陕西省自然科学基金资助项目(2016JM1031);陕西省教育厅自然科学专项基金资助项目(14JK1299)

淡静怡(1990-),女,陕西宝鸡人,西安工程大学硕士生;

薛红(1964-),男,山西万荣人,博士,西安工程大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2016.07.027

F830;O211.6

A

1003-5060(2016)07-1004-05