混合充填集料RRB方程分布特征对充填体强度影响研究

杨　啸,　杨志强,,　高　谦,　王永前,　陈得信

(1.北京科技大学 金属矿山高效开采与安全教育部重点实验室,北京　100083； 2.金川集团股份有限公司,甘肃 金昌　737100)



混合充填集料RRB方程分布特征对充填体强度影响研究

杨啸1,杨志强1,2,高谦1,王永前2,陈得信2

(1.北京科技大学 金属矿山高效开采与安全教育部重点实验室,北京100083； 2.金川集团股份有限公司,甘肃 金昌737100)

由于应用棒磨砂作为单一充填骨料制备充填体的成本过高,金川矿山面临充填成本居高不下的难题。根据金川矿山实际工程背景,文章采用成本较低的戈壁砂、选矿尾砂和棒磨砂制备混合集料,开展了不同骨料配比的充填体强度试验。为了得到不同充填集料的特征粒径评价,采用RRB(Rosin-Rammler-Bennet)模型的原数学表达式并根据最小二乘法计算出不同配比骨料的特征粒径和均匀性系数。研究结果表明:单一充填骨料制备出的充填体强度较低,充填体强度随着特征粒径的减小,均匀性系数逐渐增大，并接近1,但当棒磨砂、戈壁砂、选矿尾砂的配比为4.5∶4.5∶1时,所制备的充填体强度达到最大值。

充填骨料;RRB模型;最小二乘法;特征粒径;均匀性系数

随着环境保护法规日趋严格,具有损失率小、贫化率低、安全性高,且能有效控制采场地压活动和防治地质灾害的充填采矿法倍受采矿业青睐[1-2]。金川镍矿是我国最大的硫化铜镍矿,也是世界上特大型硫化铜镍矿之一。金川镍矿经历了强烈的地质构造运动,地质构造复杂,水平应力高,矿岩破碎,稳定性极差,岩石力学与工程稳定问题的难度被国内外同行所公认[3],因此采用充填成本高和生产能力低的下向分层胶结充填法开采。面对当前有色金属价格低迷,而金川矿山充填成本居高不下[4],探索低成本充填骨料来降低充填采矿成本,成为金川矿山的研究课题之一。

选用选矿尾砂、戈壁砂与棒磨砂混合料作为充填骨料,能够有效地降低充填骨料的生产成本[5]。研究表明，废石-尾砂混合骨料的胶结充填体强度,随着废石含量增加而提高[6]。文献[7-8]针对金川矿山充填材料,分别开展了全尾砂与棒磨砂以及全尾砂与废石混合料的合理配比试验。对多种充填骨料混合料采用RRB模型描述,获得用以表征其粒度分布特征的特征粒径De和均匀性系数n,可以方便地分析粉体粒度分布对充填体性能的影响[9-10]。采用RRB(Rosin-Rammler-Bennet)模型的原数学表达式直接根据最小二乘法原理计算得到的De和n值，与采用经变量代换后的“lnln-ln”数学形式线性回归得到的结果相比偏差较小[11]。本文根据金川矿山工程现况,运用RRB模型的原数学表达式,对棒磨砂、戈壁砂和选矿尾砂混合骨料的粒径分布进行计算分析,从而研究不同骨料配比对充填体强度的影响。

1　充填骨料物化特性

国内外矿山使用的充填骨料品种很多,主要有选矿尾砂、棒磨砂、戈壁砂、废石和河砂等。根据金川矿山实际情况以及采矿方法对充填体强度的要求,选用选矿尾砂、戈壁砂与棒磨砂的混合料作为充填骨料开展了一系列试验研究。

1.1棒磨砂

金川砂石厂棒磨机的主体工艺是将露天采出的戈壁集料砂卵石,先经破碎筛分制成粒径小于25 mm的粗集料,除部分直接送龙首矿做充填材料外,其余经棒磨机磨成小于3 mm的细砂,供二矿区充填使用。-3 mm棒磨砂基本物理化学性能见表1所列,棒磨砂、戈壁砂不同筛分孔径的筛余质量分数见表2所列。粒径级配采用S1064型激光粒度分析仪进行激光粒度测定,分布曲线如图1所示。

表1　棒磨砂、戈壁砂和选矿尾砂的物理性质与化学成分

注：ρ和容重的单位均为103kg/m3。

表2　棒磨砂、戈壁砂不同筛分孔径的筛余质量分数　%

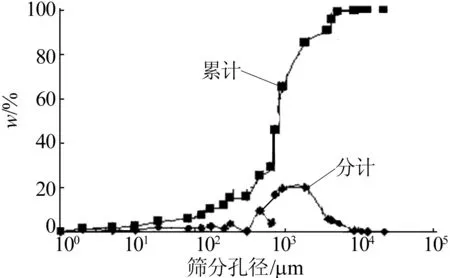
图1　棒磨砂粒级分布曲线

1.2戈壁砂

戈壁砂是露天采出的戈壁集料砂卵石,经筛分后+5 mm进入砂石厂进行棒磨加工,而-5 mm直接运至充填站砂池中用于充填。戈壁砂物理化学性能见表1所列。

戈壁砂不同筛分孔径的筛余质量分数见表2所列。

粒级分布曲线如图2所示。

图2　戈壁砂粒级分布曲线

1.3选矿尾砂

从二矿区充填站尾砂仓放出的尾砂中取样,测定其物理化学性质见表1所列。

粒级组成分析结果见表3所列,粒级分布曲线如图3所示。

选矿尾砂的分布粒径如下:d10=5.90 μm，d50=62.18 μm，d90=124.35 μm，d平均=64.55 μm。

表3　选矿尾砂粒级组成

图3　选矿尾砂粒径分布曲线

2　充填体强度试验

利用金川矿区膏体充填系统,开展了棒磨砂、戈壁砂和选矿尾砂3种骨料在不同配比条件下的充填体强度试验，试验的胶凝材料为金川矿用32.5#增强水泥。根据矿山管道自流输送充填系统工业生产指标,采用灰砂比1∶4,浆料质量分数为76%和79%。使用JJ-5型行星式水泥胶砂搅拌机,将胶凝材料、水、混合充填骨料按设计的灰砂比和料浆质量分数计算出相应的质量比,先混合搅拌180 s制成充填料浆,然后边搅拌、边注入尺寸为7.07 cm×7.07 cm×7.07 cm的三联试模中。

将试模编号放入(20±1) ℃、相对湿度不低于90%的YH-40B型养护箱中标准养护,48 h后脱模。将脱模后的充填体试块重新编号,然后放入YH-40B型养护箱继续养护,直到养护龄期。在SANS数显固定位移压机上以0.5 mm/s速度对充填体试块施加连续荷载,然后测定充填体试块(单轴)抗压强度。每个龄期测试3块,取平均值。不同骨料配比的充填体强度试验方案和结果见表4所列。表4中的骨料配比为棒摩砂、戈壁砂、选矿尾砂三者的质量比，下同。

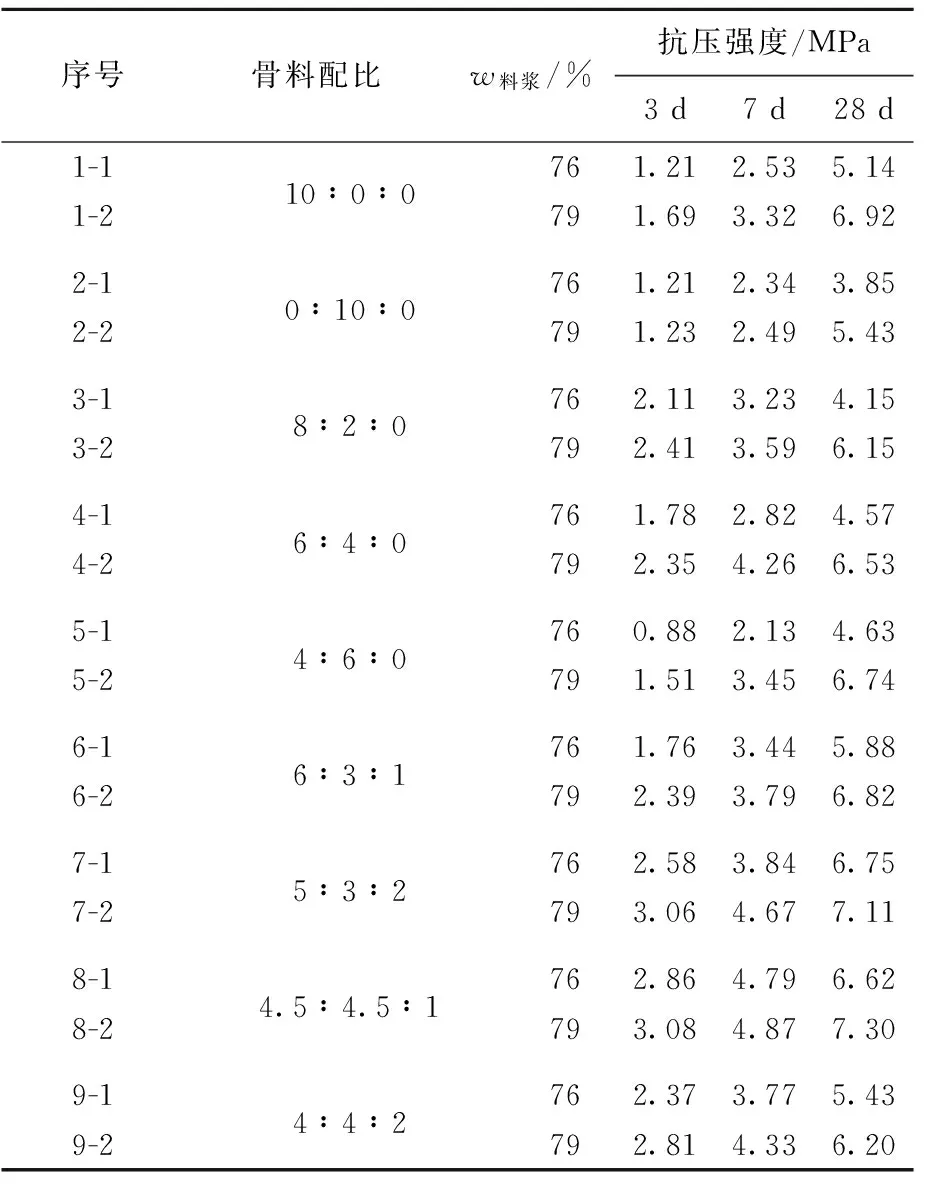
表4　混合集料胶结充填体强度试验结果

3　充填骨料粒度分布对强度的影响

为了研究混合集料配比对胶结充填体强度的影响规律,根据9组充填集料的配比以及棒磨砂、戈壁砂和选矿尾砂的粒径分布特征,按照配比加权计算出9组充填集料的粒径分布值,再由RRB方程计算出粒径特征值De和均匀性系数n。

3.1RRB方程特征粒径和均匀性系数计算

RRB分布方程表达式如下：

(1)

其中,R为粒径为D时的筛余质量分数;De为特征粒径,表示颗粒群的粗细程度,物理意义为R=36.8%时的颗粒粒径;n为均匀性系数,表示粒度分布的宽窄程度,n值越小,粒度分布范围越广。

对于某一粒径Di,其筛余质量分数Ri与模型预测值Rj之差的平方记为Δi,离差平方和记为Δ,实验总个数记为N,则根据 (1) 式可得:

(2)

(3)

由 (3) 式可见,Δ是De和n的函数,随着De和n的变化,Δ存在最小值。根据最小二乘法原理,当Δ取最小值时,对应的De和n值为采用(1)式所计算得到的最优值。欲求得Δ的最小值,可令∂Δ/∂De=0且∂Δ/∂n=0,求解联立方程组即得。

采用Matlab软件编制运算程序,由此计算出不同配比的混合集料的特征粒径De和均匀性系数n,计算结果见表5所列。

表5　不同配比的混合集料的特征粒径和均匀性系数

3.2充填体强度与特征粒径的关系

由不同配比混合集料的充填体3、7、28 d强度与对应混合集料的特征粒径关系如图4所示。

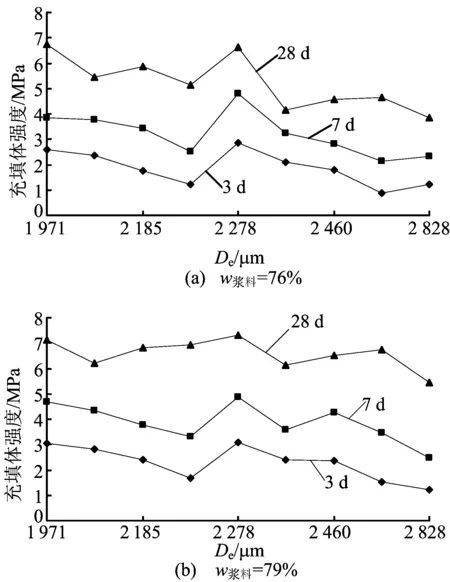
图4　不同骨料配比充填体强度与特征粒径关系

图4中特征粒径为2 213 μm和2 828 μm分别对应单一充填骨料棒磨砂和戈壁砂。由图4可以看出,单一充填骨料制备的充填体3、7、28 d强度均低于混合充填骨料。而在特征粒径2 278 μm时,即充填骨料棒磨砂、戈壁砂、尾砂的配比为4.5∶4.5∶1,充填体的3、7、28 d强度达到了最大值。剔除强度最大值的骨料配比与单一充填骨料,作出混合骨料充填体强度与特征粒径关系曲线如图5所示。

图5　混合骨料充填体强度与特征粒径关系

从图5可以看出,随着充填骨料特征粒径增大,3 d和7 d充填体强度随之减小,而28 d充填体强度在特征粒径2 337 μm之后呈轻微上升趋势。

3.3充填体强度与均匀系数的关系

由于有2组充填骨料均匀性系数为0.984,且其中一组是强度最大值的骨料配比,所以将均匀性系数为0.984的2组充填体强度数据剔除后,可得混合骨料充填体强度与均匀性系数关系如图6所示。从图6可以看出,均匀性系数在1以下时,随着均匀性系数增大,充填体强度逐渐增大;但均匀性系数在1以上时,随着均匀性系数增大,充填体强度逐渐减小。

图6　混合骨料充填体强度与均匀性系数关系

4　结　　论

为了安全可靠地利用戈壁砂和选矿尾砂作为金川镍矿充填法采矿的充填骨料,本文开展了棒磨砂、戈壁砂和选矿尾砂3种充填骨料在不同配比条件下的胶结充填体试验,由试验可得以下结论:

(1) 使用单一充填骨料制备出的充填体比使用混合骨料制备出的充填体强度低。

(2) 采用棒磨砂、戈壁砂、选矿尾砂配比为4.5∶4.5∶1的混合骨料时,制备出的充填体强度达到最大值。浆料质量分数为76%时3、7、28 d强度分别为2.86、4.79、6.62 MPa,浆料质量分数为79%时3、7、28 d强度分别为3.08、4.87、7.30 MPa,均符合金川矿山对充填体强度的要求。同时这种充填骨料的成本远低于传统的棒磨砂充填骨料。

(3) 随着混合充填骨料特征粒径的增大,充填体早期强度呈下降趋势,但后期强度在特征粒径2 337 μm之后呈上升趋势。

(4) 充填骨料的均匀性系数越接近1,充填体强度越大。

[1]谢龙水.矿山胶结充填技术的发展[J].湖南有色金属,2003,19(4):1-5.

[2]赵传卿,胡乃联.充填胶凝材料的发展与应用[J].黄金学报,2008,29(1):25-29.

[3]陈仲杰,杨金维.金川矿区深部高应力碎胀蠕变岩体支护对策[J].金属矿山,2005(1):18-22.

[4]王正辉.金川矿山废料胶结充填工艺技术研究[J].采矿技术,2011,11(4):32-36.

[5]杨志强,王永前,高谦,等.金川镍矿尾砂膏体充填系统工艺技术改造与应用研究[J].有色金属科学与工程,2014,5(2):1-9.

[6]郭利杰,杨小聪.废石尾砂胶结充填试验研究[J].武汉理工大学学报,2008,30(11):75-78.

[7]杨志强,王永前,高谦,等.全尾砂棒磨砂混合充填料浆的优化配比试验研究[J].中国矿山工程,2013,42(6):1-5.

[8]乔登攀,姚维信.金川矿山废石-全尾砂高浓度充填工艺试验研究[J].有色金属科学与工程,2011,2(6): 57-61.

[9]赵旭光,文梓芸,赵三银,等.高炉矿渣粉的粒度分布对其性能的影响[J].硅酸盐学报,2005,33(7):907-915.

[11]赵三银,赵旭光,余其俊.RRB分布模型特征粒径和均匀性系数的准确计算[J].有色矿冶,2006,22(增刊1):49-52.

(责任编辑闫杏丽)

Research on the influence of mixed filling aggregate distribution based on RRB model on filling body strength

YANG Xiao1,YANG Zhiqiang1,2,GAO Qian1，WANG Yongqian2,CHEN Dexin2

(1.Key Laboratory of High Efficient Mining and Safety of Metal Mines of Ministry of Education, University of Science and Technology of Beijing, Beijing 100083, China; 2.Jinchuan Group Co., Ltd., Jinchang 737100, China)

Due to the fact that the cost of rod-mill tailings using as single filling aggregate is too high, Jinchuan Mine is faced with the problem of high filling cost. In view of the engineering environment of Jinchuan Mine, the aggregate mixed with low-cost gobi sand, mill tailings and rod-mill tailings was prepared, and then the strength tests of the filling body with different aggregate ratios were carried out. In order to get the characteristic particle size evaluation of different filling aggregates, the original mathematical expression of Rosin-Rammler-Bennet(RRB) model was used and the characteristic particle size and uniformity coefficient of different aggregates were calculated by using the least squares method. The results show that the strength of the filling body made with the single filling aggregate is lower than that made with the mixed aggregate. And the strength of filling body increases gradually with the decrease of characteristic particle size and the uniformity coefficient is close to 1. When the aggregate ratio of rod-mill tailings, gobi sand and whole-tailings is 4.5∶ 4.5∶ 1, the strength of filling body reaches the maximum.

filling aggregate; Rosin-Rammler-Bennet(RRB) model; least squares method; characteristic particle size; uniformity coefficient

2015-03-19；

2015-05-25

国家高技术研究发展863计划资助项目(SS2012AA062405)

杨啸(1988-),男,河南郑州人,北京科技大学博士生;

高谦(1956-),男,江苏徐州人,博士,北京科技大学教授,博士生导师.

10.3969/j.issn.1003-5060.2016.07.020

TD863

A

1003-5060(2016)07-0965-05