桁架结构损伤预测方法初探

陈诗超　陈建飞

(阳光学院土木工程系　福建福州　350015)



桁架结构损伤预测方法初探

陈诗超陈建飞

(阳光学院土木工程系福建福州350015)

综合运用模态曲率变化量与模态应变能变化率，提出了桁架结构损伤预测的方法。首先，应用ANSYS有限元软件建立梁式桁架的模型，分析其位移模态并模拟其损伤，并通过分析桁架上下弦的模态曲率变化量预测损伤区域。其次，计算损伤区域内杆件的模态应变能变化率，并将应变能变化率较大的杆件认定为损伤单元。数值模拟结果表明，该法可准确定位梁式桁架的损伤部位。

损伤预测；桁架结构；模态曲率变化量；模态应变能变化率

0　引言

相对于其他结构型式，桁架结构可以极大地节约材料。该结构可以在相同的竖向挠度限制下获得更大的跨度，并且可以方便、迅速地安装，因此在大跨度铁路桥中大量运用了该结构型式。随着对结构健康监测需求的增长，越来越多的学者开始关注结构损伤的识别，也因此提出了一系列的方法[1-2]。总体来说，模态曲率变化量法广泛用于梁式结构的损伤鉴别[3-5]，模态应变能变化率法则用于桁架结构[6-8]。

梁式结构中杆件众多，下弦杆的模态曲率变化量仅能甄别可能的破坏区域，而不能定位破坏杆件。虽然模态应变能变化率可以鉴别破坏的杆件，但需要分析的杆件数量较大，同时分析结果并非十分准确[6]。因此，本文将模态曲率变化量法与单元应变能变化率法相结合，提出了结构损伤预测的两步法。首先，按照第一阶模态的曲率变化定位可能的损伤区域，随后计算可能损伤区域内杆件的应变能变化率，以最终确定真正的损伤杆件。所进行的数值模拟表明：本文提出的损伤预测法适用于梁式桁架结构损伤的预测。

1　基本原理

1.1模态曲率(MC)

学术界多采用结构的位移描述其振动模态，本文所采用的模态曲率，其作为受弯结构中性层变形的描述，则显得更为精确。直梁轴线的曲率可以通过下列弯曲变形近似微分方程计算：

(1)

式中的x是沿梁长度方向的坐标，y则是梁的挠度。式(1)在节点i处的微分形式则可写成：

(2)

在本文中，将较大模态曲率变化量节点所围成的区域作为可能的损伤区域。

1.2模态应变能变化率(MSECR)

随着结构刚度的降低，损伤单元的模态应变能将随之改变。由于第一步中已经定位了损伤区域，因此对其中的杆件进行应变能变化量的分析是可行的。模型第j单元i阶模态的应变能可以表示为如下形式：

MSEij={φi}T[Kj]{φi}

(3)

式(3)中Kj为第j单元的结构刚度矩阵，φi为第i阶模态，另外d表示损伤的结构。

由于Kj、φi均过于庞大，为了节约计算资源，可以采用单元刚度矩阵ki代替Ki，同时采用单元节点向量vi代替φi：

MSEij={vij}T[kj]{vij}

(4)

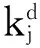
因此应变能改变率(MSECRij)可以按照下式计算

(5)

实际应用的过程中，可以采用多阶模态的复合应变能改变率(MSECRj)减小噪音：

(6)

损伤单元即为最大复合应变能改变率(MSECRj)所在的单元。

2　数值模拟

本文采用ANSYS，建立了一个两端铰支的梁式桁架的数值模型，模型具体尺寸如图1所示，杆件的材料属性详见表1。该数值模型采用35个Link1单元模拟杆件，计算所得未损伤结构的一二阶模态如图2所示。研究过程中通过降低杆件的刚度模拟结构的损伤。

2.1下弦杆损伤的模拟

假设3号杆件受到损伤后，刚度分别降低5%、10%、 20% 及 50%，上下弦杆第一阶模态曲率变化量如图3所示。由图3可知，3号、4号节点数值较大，这就意味着下弦杆的3、4号节点位于破坏区域。对于上弦杆，显然节点13位于破坏区域。因此破坏区域由3号、4号、13号节点围成，即破坏杆件应该在3号、14号、15号杆件中。

接着计算3号、14号、15号杆件的模态应变能变化率，并将结果列于表2。对于不同的损伤工况，均可以按照最大的模态应变能变化率确定3号杆为损伤杆件。

2.2边界杆件的损伤模拟

由于采用了微分算法，实际上我们无法得到支撑节点的模态曲率变化量。如果边界位置的杆件发生破坏，上下弦杆间的模态曲率变化量峰值点将在一条直线上，而不是围成一个区域。现假设10号杆件受到损伤，且损伤程度为5%、10%、20% 及 50%。上、下弦杆的第一阶模态曲率变化量如图4所示。由图4可见：模态曲率变化量的峰值出现在2号及12号节点，因此破坏区域应处于节点的连线左侧，即可能的破坏杆件为1号、10号、11号、28号杆。

1号、10号、11号、28号杆的模态应变能变化率的计算如表3所示，表中数据可知：损伤单元应该为具有最大值的10号杆件。

2.3多位置损伤

假设2号、33号杆件受到损伤，损伤程度为10%。上下弦杆的第一阶模态曲率变化量如图5所示。由图5可知：上弦杆的模态曲率变化量峰值出现于12号、16号、17号节点，下弦杆的峰值这出现于2号、3号、7号节点。此时，由这些节点所围成的损伤区域有两个，可能的损伤杆件分别为为2号、12号、13号和21号、22号、23号杆件。将这些杆件的模态应变能变化率计算结果列于表4，由计算结果可知：损伤杆件为具有较大变化率的2号、3号杆件。

3　结论

本文通过将模态曲率变化量法和模态应变能变化率法结合，提出了梁式桁架损伤的预测方法。方法将损伤预测分为两部分：其一，通过模态曲率变化量定位可能的损伤区域；其二，依据模态应变能变化率准确确定损伤杆件。本文的数值模拟结果表明：无论桁架损伤的位置如何，本文所提供的方法都可以准确定位损伤的杆件。

[1]YU Ling, ZHU Junhua, YU Lili. Structural Damage Detection in a Truss Bridge Model Using Fuzzy Clustering and Measured FRF Data Reduced by Principal Component Projection [J]. Advances in Structural Engineering, 2013, 16:207-217.

[2]Sazonov E, Klinkhachorn P. Optimal Spatial Sampling Interval for Damage Detection by Curvature or Strain energy Mode Shapes [J]. Advances in Structural Engineering, 2013, 16:207-217. Journal of Sound and Vibration, 2005, 285:783-801.

[3]Dawari V B, Vesmawala G R. Modal Curvature and Modal Flexibility Methods for Honeycomb Damage Identification in Reinforced Concrete Beams [J]. Procedia Engineering, 2013, 51:119-124.

[4]Baghiee N, Esfahani M R, Moslem K. Studies on Damage and FRP Strengthening of Reinforced Concrete Beams by Vibration Monitoring[J]. Engineering Structures, 2009, 31: 875-893.

[5]叶黔元, 翟立祥, 陈锦辉. 曲率模态及其在桁架桥梁损伤识别中应用 [J].力学季刊, 2005, 26:286-292.

[6]Seyedpoor S M. A Two Stage Method for Structural Damage Detection Using a Modal Strain Energy Based Index and Particle Swarm Optimization [J]. International Journal of Non-Linear Mechanics, 2012, 47:1-8.

[7]Yan W J, Ren W X, Huang T L. Statistic Structural Damage Detection Based On the Closed-form of Element Modal Strain Energy Sensitivity [J]. Mechanical Systems and Signal Processing, 2012, 28:183-194.

[8]史治宇, 罗绍湘, 张令弥. 结构破损定位的单元模态应变能变化率法 [J].振动工程学报, 1998, 11:356-360.

陈诗超(1988.03-)，男，助教，主要从事冲击动力学、结构健康监测与检测方向的研究。

陈建飞(1987.12-)，男，助教，主要从事土体注浆加固方向的研究。

A Prieliminary Study on Damage Forecast Method for Truss Structure

CHENShichaoCHENJianfei

(Department of Civil Engineering,Yango College,Fuzhou 350015)

By integrated use of Variation of modal curvature and Rate of modal strain energy changing，a damage forecast method for truss structure is proposed. Firstly, a finite element model of truss structure is established with ANSYS，after which displacement modes are got and damage is simulated，the damage region is estimated via analyzing the variation of modal curvature of top and bottom chords of truss structure. Subsequently, the modal strain energy changing rate of members in the damage region is calculated and the element with the maximum modal strain energy changing rate is deemed as the damaged element. The simulation results show that this method can accurately locate the damage in the beam-like truss structure.

Damage forecast；Truss structure；Variation of modal curvature; Rate of modal strain energy changing

陈诗超(1988.03-) ，男，助教。

E-mail:ligong0601@163.com

2015-12-01

TU3

A

1004-6135(2016)02-0043-05