汽车塑料构件开发中CAE计算结果准确性探讨
张静秋,刘建元
(广东科技学院,广东东莞 523083)
汽车塑料构件开发中CAE计算结果准确性探讨
张静秋,刘建元
(广东科技学院,广东东莞 523083)
CAE 软件能够提供从分析部件性能到系统级设计所需的全部工具,可用于众多类型的汽车仿真分析。但CAE技术原理决定了CAE计算结果的准确性是有其适用范围和极限的。特别是针对塑料零件的设计分析,CAE计算结果的准确性问题尤其值得关注。分析了影响CAE计算结果准确性的主要因素。精心选择了3个应用案例:特征频率预测、振动应力计算和疲劳分析,来说明CAE仿真结果的准确性问题。第一个案例的研究结果表明:CAE仿真能够对结构体整体性能,诸如特征频率等,进行非常准确的预测。而第二个案例证实:结构体由振动引起的应力、应变,使用CAE仿真计算得到的结果和试验结果却不吻合。第三个案例,即使是疲劳预测这种众所周知的难题,使用CAE仿真计算对比结构体A、结构体B(结构体A的改进)的性能变化,结果却很准确。以上案例说明,在塑料零件设计评估中,应该更加重视CAE对零件整体性能的仿真结果,而不是去关注局部特性。此外,凡是需要预测局部特性时,一定要优先考虑从A到B的对比。如果必须对由CAE仿真得到的应力、应变做出说明,则一定要结合其他的评估手段,以避免对设计造成误导。
汽车;塑料;CAE仿真;准确性
0 引言
不断变化的市场前景、消费者需求以及新的政策法规都推动着汽车行业积极地进行创新,以提高燃料效率、改进噪声振动性能并降低材料成本。作为新兴技术的早期采用者,这一行业期待着能够实现这些目标的仿真解决方案。CAE软件的解决方案处于这场革命的前沿,尤其是所有大型 OEM 和关键供应商已将这些软件产品运用到设计和开发流程之中。为使工程部门能够更加高效地实现更高层次的创新,CAE 软件能够提供从分析部件性能到系统级设计所需的全部工具。
目前CAE软件可用于众多类型的汽车仿真,涉及设计优化、噪声与振动、声学、耐久性与疲劳、碰撞与安全、乘坐与操控、非线性与接触建模、零部件与组合件结构分析、复合材料建模、热特性、机电一体化、车辆动力学,以及多学科分析等众多领域[1-2]。每一种应用都有其自身的特点和规律,作者仅就CAE技术在汽车塑料构件开发过程中存在的问题做一些分析。
采用复合材料设计、制造的部件和产品具有众多优势——轻质、坚实、耐用及耐热,它们取代了铝和钢等金属,为许多行业所认可,在汽车行业更是如此。作为“工程材料”的复合材料能为产品制造商带来质量及性能等多方面的优势。但相对金属之类的常规材料而言,它们在产品设计中也存在着诸多难题。分层、引起最终断裂的微裂以及其他一些在采用金属进行设计时不会遇到的情况,对于复合材料而言均非常重要。由于制造工艺昂贵、耗时,使得实体模型更加不现实。CAE软件在复合材料方面广泛的解决能力有助于复杂复合材料的分析与设计改进[3-5]。
然而,CAE预测结果的准确性依然受到质疑,尤其是当计算结果与设计师预期的结果相悖时,特别是到了设计晚期。CAE计算结果建议对设计做出修改,这一修改建议应否被采纳,经常引发争论。更严重的是,有时CAE计算结果会与试验结果完全不同。复合材料的特性会使这一问题更加严重[6]。
1 引发CAE计算偏差的根源
设计工程师有很多理由怀疑CAE计算结果的准确性。虽然计算机软、硬件技术快速发展,使得今天的CAE模型,较之以往更接近真实结构,然而,CAE仿真过程中,假设与简化依然不可避免。
首先,有限元的网格只是对真实表面或空间的一种近似,从来不能真正代表真实的几何构造。例如,一些并不是很重要的几何特征,像倒角等,经常被省略掉。删除壳模型中的某一表面而造成的间隙,会导致表面连接的近似。此外,在壳模型中,由拔模角引起的壳厚的微小变化,也可能被忽略。
根据圣维南原理,边界条件通常被理想化,即应力分布假设,除载荷点外,并不考虑真实的负载分布。而由于载荷集中,在结构边界位置,应力通常会达到峰值,这恰好是塑料零件设计成功的关键。这也说明,为何在塑料零件结构连接处和载荷点处,通过CAE仿真计算预测应力尤其困难。此外,不同类型约束的机构建模不当,会引发更多的错误。对6个自由度全部被约束的边界,用螺栓、螺母方式建模是最直接的方法,而预紧式的锁扣连接则很难建模。当一个塑料部件由几个不同的零件组装而成时,对连接部位建模是一件非常有挑战性的工作。为仿真真实物理现象,连接位置需要做接触建模。然而,在CAE中对连接位置进行细致的建模,会消耗大量计算资源,有时甚至会导致仿真计算结果离散。因此,在实际应用时,经常使用诸如刚性连接等简化方法,这种简化可能也会导致CAE计算结果错误。
与传统金属材料相比,塑料的应力、应变特性具有典型的非线性。分子结构、化学成分或填料的细微变化都会明显改变材料特性。同时,塑料特性对温度和湿度等环境条件也极为敏感。时变性,也是所有塑料的另外一种特性。应力、应变曲线会随加载时间的变化而变化,蠕变和放松也具有同样的现象。所有这些因素,使得CAE工程师很难获得材料的真实非线性特性。
此外,加工过程使得塑料特性变得更加复杂。例如,喷铸零件内部从注塑口到模具末端有密度梯度;熔化的塑料流动过程中,会使聚合物沿流动方向排布,这使得塑料呈各向异性[7];塑料件焊线位置强度通常会降低,是整个塑料结构性能的薄弱点。
所有这些因素,都会影响CAE计算结果的准确性。关于各因素的分析研究,可以检索到大量文献。在此作者只讨论工业环境下,CAE计算结果的准确性和可靠性。
汽车工业中,学术研究项目与设计分析的根本区别,在于CAE模型输入信息的准确性与实用性。众所周知,CAE仿真在产品设计的初期更有价值,因为问题发现得越早,修正耗费越少。然而,越是早期,可供计算使用的准确信息就越少。
设计早期,设计细节在CAD中并不完善。有时,结构间安装关系还没有确定,这直接影响CAE仿真;有时,材料甚至还没有确定,而寄希望于CAE仿真结果能够帮助确定材料;有时即使材料已经确定,材料供应商却不能提供所需要的材料信息或提供的信息不够准确。此外,缺少载荷信息也是导致计算错误一个重要因素。在载荷定义不足或没有定义的情况下进行CAE分析,这种情况也很常见,尤其是动态载荷。这里有几种原因:没有产品或原型机进行准确的载荷测试;交付时间受限;加载情况太复杂,不能定义或测试。缺少准确的输入条件,必然会导致CAE预测不准。因此,如何在工业应用中解读CAE计算结果,成为CAE分析人员或产品工程师的一项重要工作。
2 CAE分析案例
通过Y ZHANG等所做关于CAE准确性的3个应用案例[8],即特征频率分析、振动应力分析和疲劳分析,来说明CAE仿真计算的准确性和局限性。
2.1塑料零件特征频率分析
试验装置:一套转向灯,固定金属板,激振器。激振器能够在垂直方向产生5~200 Hz、1g大小的振动。一个加速度传感器直接安装在夹具中心,用来测量激振器传递给夹具的加速度值。另外两个加速度传感器安装在转向灯上部固定点处,分别用来测量横向和纵向的振动响应。特征频率测试试验台见图1。

图1 特征频率测试试验台
测试的频率-时间曲线见图2。响应曲线中的峰值表示灯组的共振频率点。
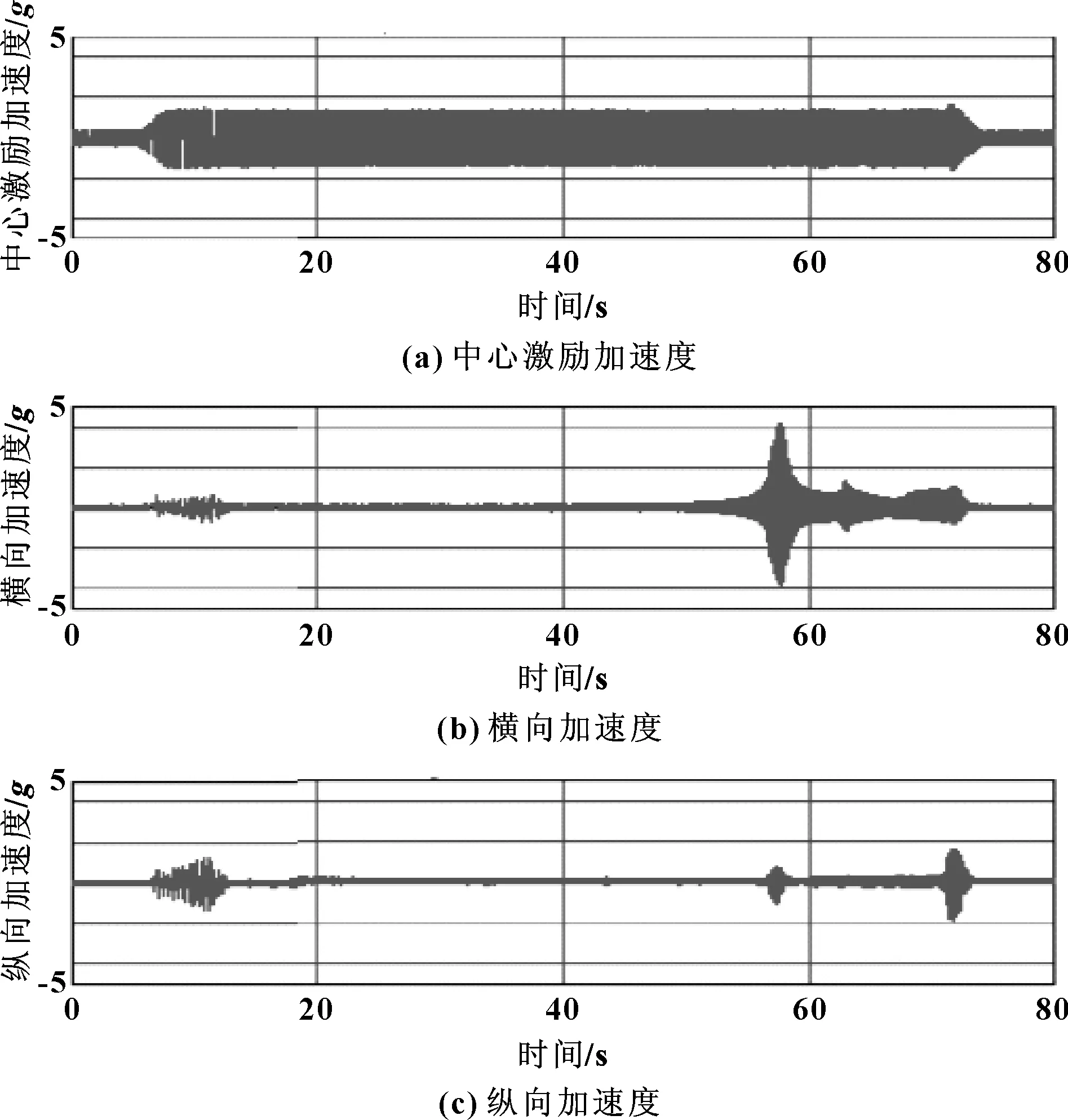
图2 振动信号输入和输出时间曲线
图3用频率增益指标,清晰地显示出了灯组的第一特征频率为89 Hz。增益,即给定频率点输出频率幅值与输入频率幅值的比值,便于辨别共振点。
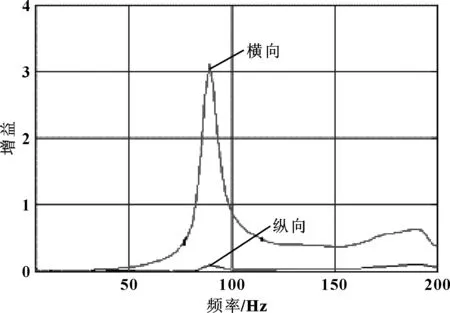
图3 灯具横向和纵向频率增益曲线
用CAE软件建立了灯组的仿真模型,并计算了灯组的特征频率。灯壳由聚碳酸酯材料制作,弹性模量2.3 GPa,密度1.11 g/cm3;灯透镜由丙烯酸材料制作,弹性模量1.7 GPa,密度1.16 g/cm3;测试安装板由1010钢制作,弹性模量203 GPa,密度7.86 g/cm3。
模型分析由商业软件NASTRAN完成,计算结果显示灯组
第一特征频率为92 Hz,如图4所示,与测试结果相比只有3.4%的偏差。
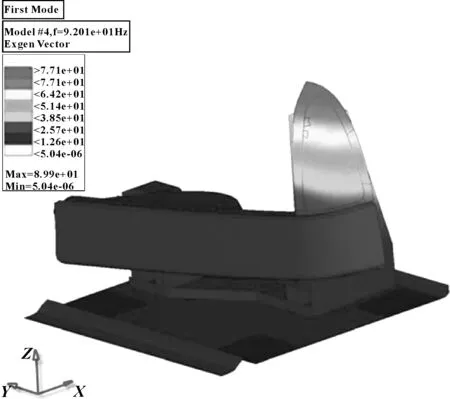
图4 用CAE软件计算的灯组第一特征频率
这一案例表明,CAE可以准确计算塑料构件的第一特征频率。类似的CAE计算结果进一步证明,CAE能够很准确地预测结构整体性能,比如特征频率、位移、结构刚度等[9]。
2.2振动应力计算
对一款头灯进行了FMVSS108振动测试。使用一个三向加速度传感器测量测试基座中央靠近头灯安装位置的输入振动加速度值。一个应变传感器安装在头灯的一个固定连接处,用来测量应变反应。试验情况如图5所示。振动器产生的振动输入信号如图6所示,应变测试结果如图7所示。
使用NASTRAN建模,利用瞬态方法计算了应变测试部位的应力响应。头灯建模如图5所示。灯壳由聚丙烯材料制作,弹性模量3.5 GPa,密度1.23 g/cm3;灯罩和反光板用聚碳酸酯材料制作,弹性模量2.0 GPa,密度1.22 g/cm3;反光镜由聚醚酰亚胺材料制作,弹性模量3.0 GPa,密度1.28 g/cm3;试验台材料为1010钢。
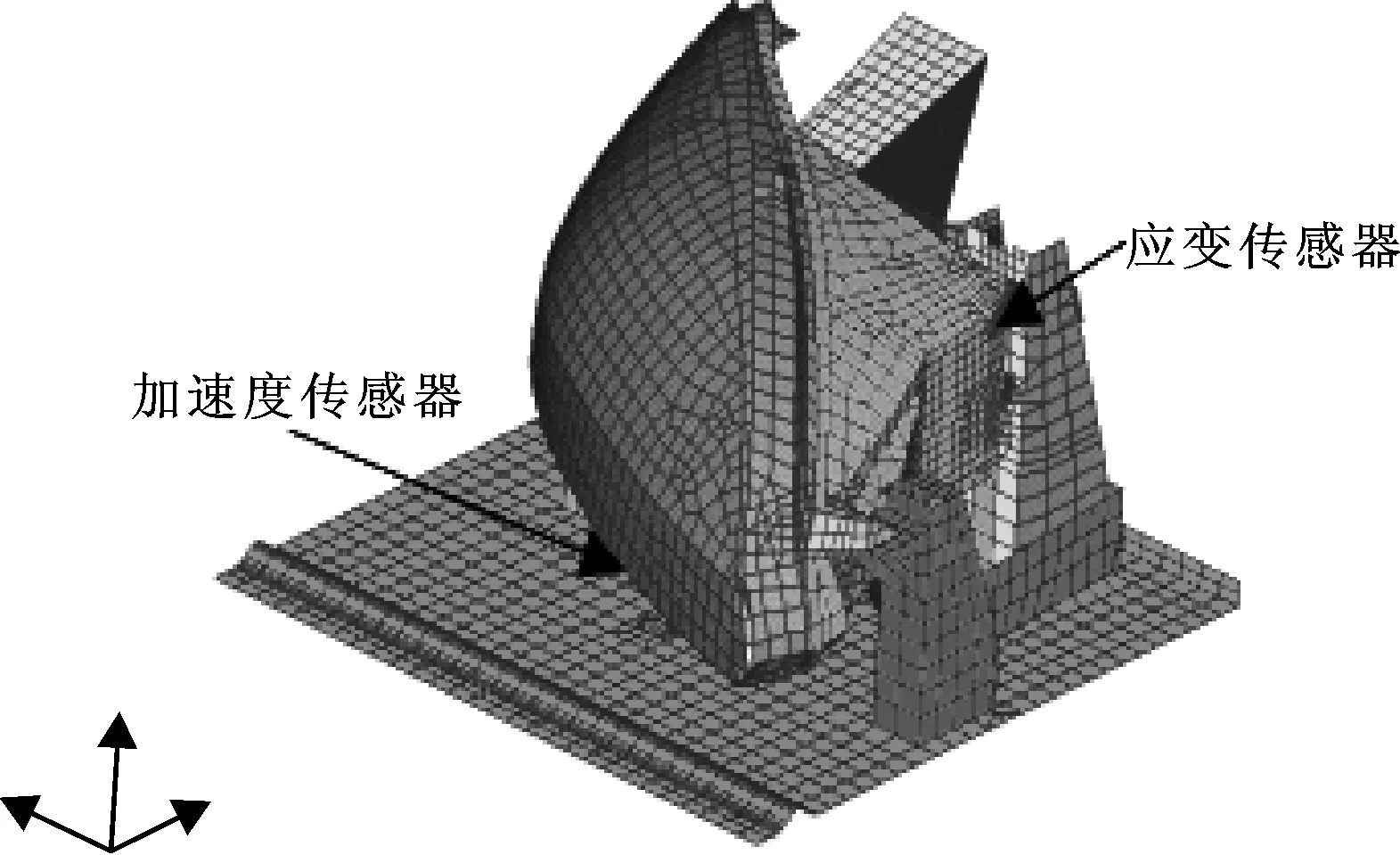
图5 头灯测点和CAE模型
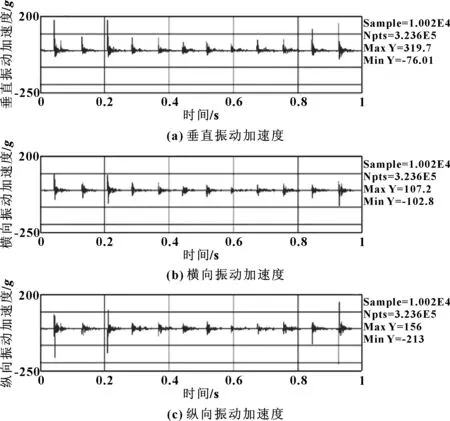
图6 输入激振信号
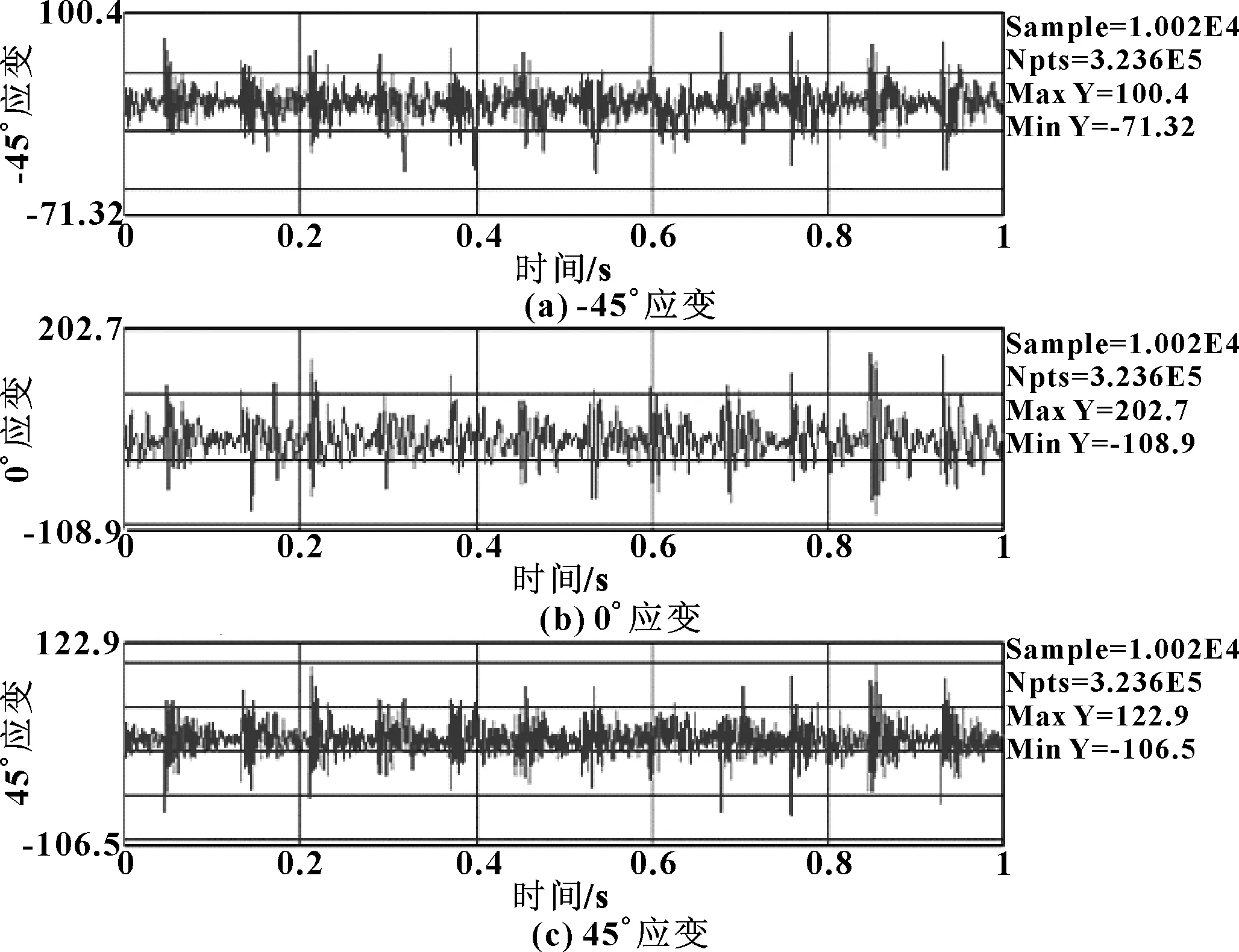
图7 输出应变信号
由应变测试结果计算得来的主应力和CAE仿真结果均列于图8中。
之所以选择主应力来比较,主要为了消除应变传感器安装位置的影响。结果很明显,CAE仿真结果值偏高(峰值1.1 MPa),而实测值只有0.55 MPa,偏差100%。虽然两者的均方根值很相近,计算结果0.16 MPa,测试结果0.17 MPa。
这一案例清楚地说明,想通过CAE准确预测塑料元件应力,相当困难。因此,在解读CAE计算出来的应力结果时,需要通过其他途径来补充信息[10]。在开发塑料零件时,决策过程应该更重视CAE计算出的结构整体性能信息,而不是局部的应力、应变信息。只要有可能,应该首先建立结构整体性能标准,比如变形限值、最小第一特征频率等。
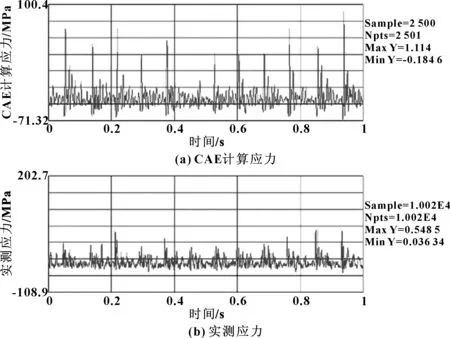
图8 应变响应的CAE仿真与试验对比
2.3疲劳分析
在一个支架疲劳振动试验中,当振动试验进行到8 min时,连接位置出现破坏。如图9所示,在T形连接的一个弯角处出现断裂。为提高连接处疲劳寿命,T形连接被加厚。那么,改进后的结构能否通过振动试验呢?为回答这个问题,需要进行疲劳寿命计算。

图9 支架振动破坏
普遍认为,准确计算疲劳寿命是一件很困难的工作,即使导致疲劳破坏的应力被准确测到[11-13]。何况,在此案例中,弯角处的应力值是很难测到的。因此,只能借助CAE计算,对应力水平做出评估,同时预测疲劳寿命。可是, CAE计算应力是有局限的,在此采用另一种办法,即直接对比两种结构的计算结果。
初始安装结构模型如图10所示,改进结果如图11所示。在连接方向施加1 N的载荷,用ABAQUS分别计算两种结构的应力响应。结构材料为ABS塑料,弹性模量2.4 GPa,密度1.06 g/cm3。计算结果显示,施加载荷后,失效位置的应力有所下降,由原来的0.83 MPa降到0.54 MPa。
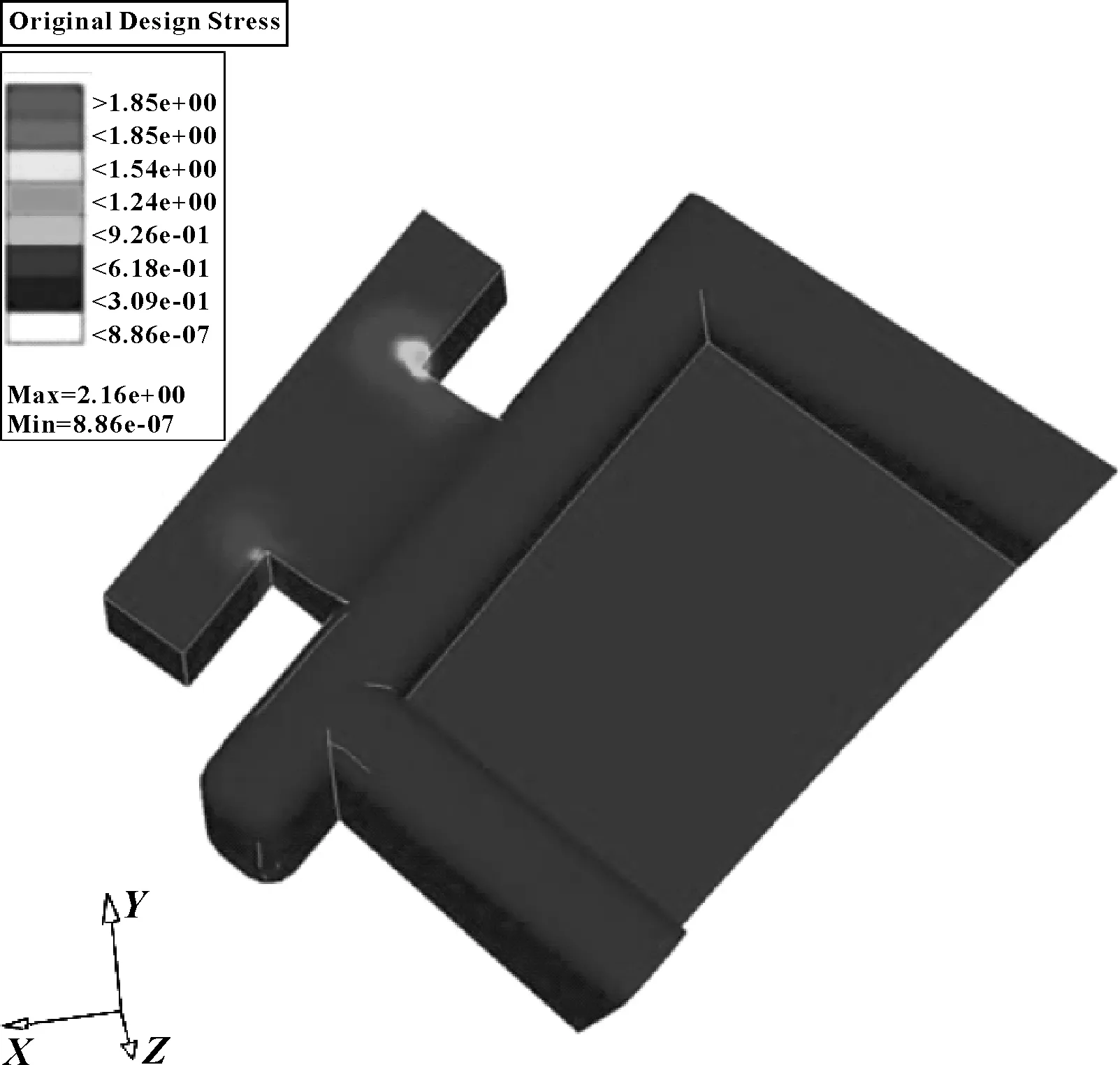
图10 原始结构的CAE仿真结果
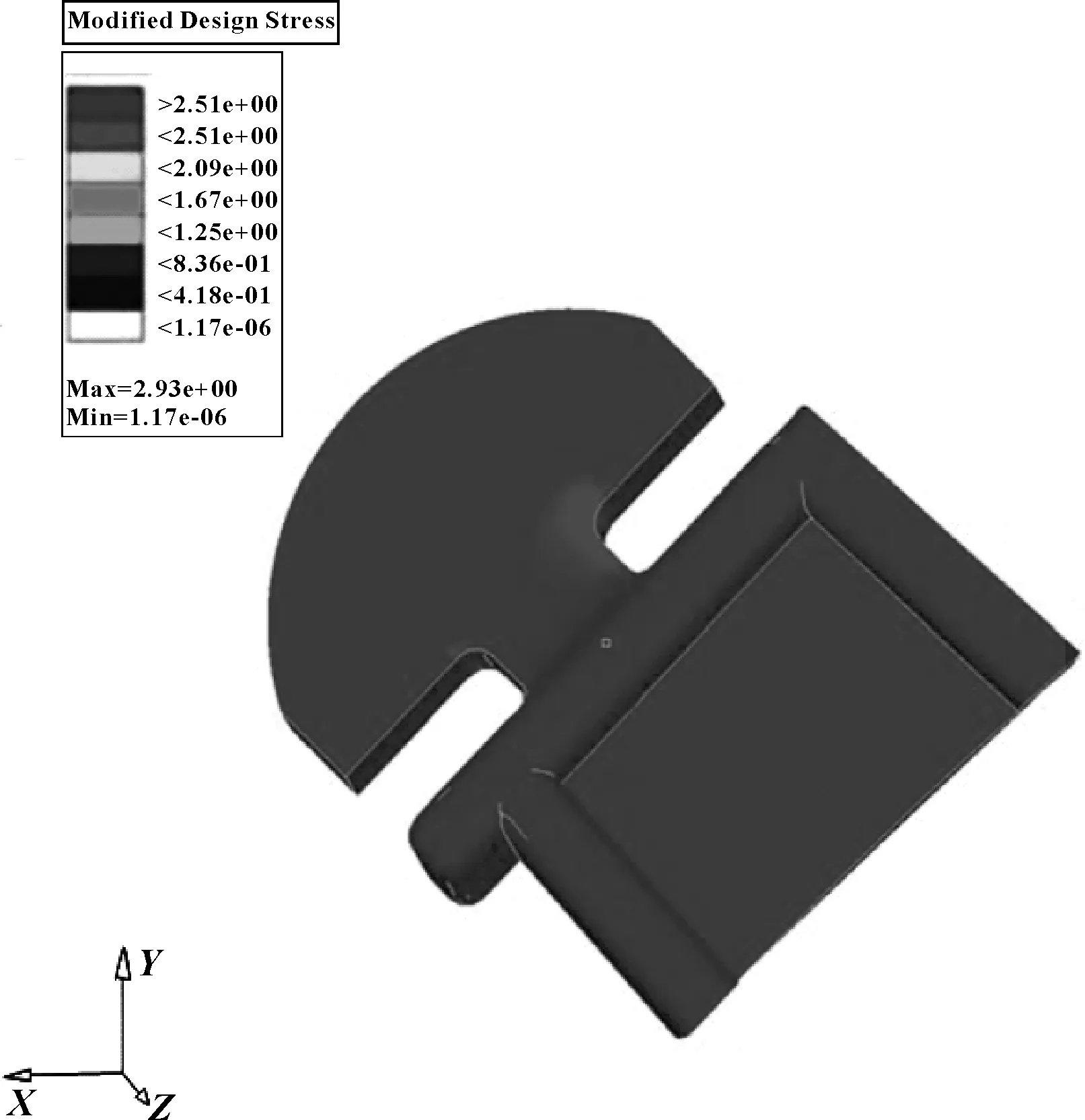
图11 改良结构的CAE仿真结果
由材料商提供的ABS材料应力-寿命曲线如图12所示。趋势寿命可通过公式(1)来预测。
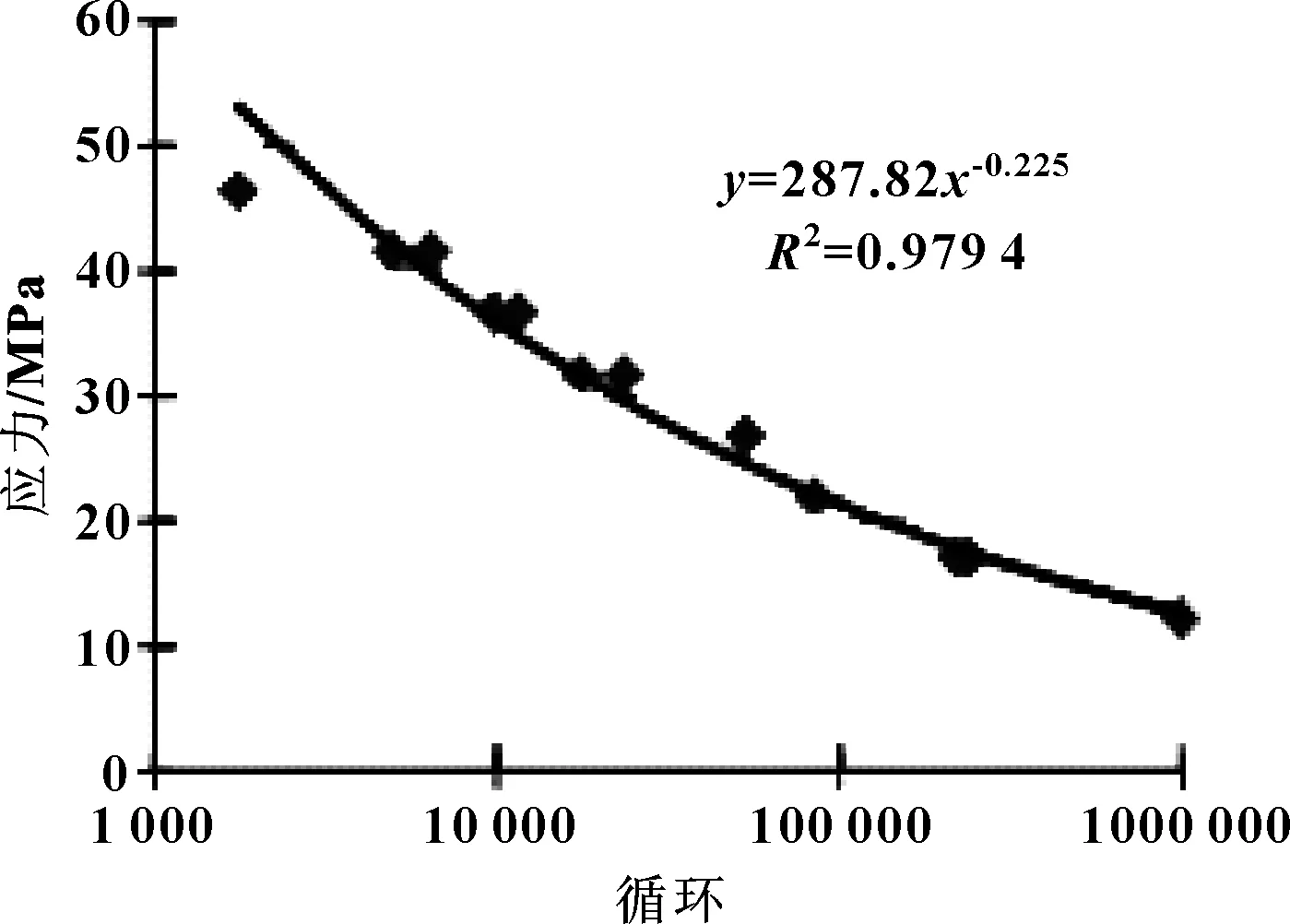
图12 应力-寿命曲线
S=290N-0.226 4
(1)
对于不同的应力水平,疲劳寿命可用公式(2)来估算:
(2)
式中:S1和N1分别是改进结构的应力和疲劳寿命;S0和N0分别是初始结构的应力和疲劳寿命。
使用公式(2),可以预测新结构能够持续54 min。实际测试结果65 min,与预测值很接近。
此案例研究表明:虽然有时准确预测应力和疲劳寿命的绝对值很困难,但是如果CAE技术使用得当,还是能够高效、准确地对结构性能进行评估。这样说并不表示对所有CAE软件都首选这种比较分析方法。
3 结论
汽车工业已经离不开CAE技术的支持,但CAE技术在大规模应用的过程中,需要认真研究、具体分析对象自身的特点,充分发挥CAE技术的优势,同时克服CAE技术的不足。
前两个案例,展示了CAE方法的优势和弱势。概括说,CAE能够准确预测结构整体性能,比如位移、刚度和特征频率等;而预测局部参数,如应力、应变时,却严重背离实验结果。
几个根本原因导致了CAE计算偏差。
(1)应力、应变由位移微分得来,应力、应变收敛的速度比位移慢很多。
(2)有限元网格质量对计算结果的准确性有很大影响。
(3)材料不统一也是一个问题,比如由注塑过程引起的密度变化和流动方向,对应力、应变位置有很大影响,虽然对整体性能也会有影响,但表现出来的已经是一个平均的结果。
(4)结构细节的微小变化,比如去掉一个倒角,对结构整体性能,如位移、刚度影响甚微,但众所周知,尖角处会产生应力集中。
第三个案例表明,虽然有时准确预测塑料零件局部应力、应变比较困难,但CAE做A到B比较分析时,依然是准确有效的。因此,如果有可能,在做CAE分析时,做A到B的比较分析是首选。
当在没有早期试验结果支持的情况下,必须对CAE计算的应力、应变做出解释时,需要结合相关的试验数据,针对CAE计算结果制定一个安全系数。
【1】林建兵.汽车内饰件注塑成型数值模拟及缺陷分析[J].制造业自动化,2015,37(7):106-108.
LIN J B.The Car Inner Decoration Molding Numerical Simulation and the Analysis of Defects[J].Manufacturing Automation,2015,37(7):106-108.
【2】杨斌,李延杰.CAE技术在汽车仪表板模具设计中的应用[J].工程塑料应用,2005,33(3):61-63.
YANG B,LI Y J.Application of CAE Technology in the Mold Design of Car Panel[J].Engineering Plastics Application,2005,33(3):61-63.
【3】章柱衡,肖小亭,朱海燕.轿车保险杠顺序注射成型CAE分析[J].工程塑料应用,2010,38(10):31-35.
ZHANG Z H,XIAO X T,ZHU H Y.CAE Analysis of Plastic Sequence Injection Process of Car Bumper[J].Engineering Plastics Application,2010,38(10):31-35.
【4】杜亭,戴隆明,章志兵,等.汽车覆盖件设计全流程CAD/CAE系统开发与应用[J].材料科学与工艺,2010,18(4):494-498.
DU T,DAI L M,ZHANG Z B,et al.Research and Application of CAD/CAE System for the Whole Development Cycle of Automotive Panel[J].Materials Science & Technology,2010,18(4):494-498.
【5】林建兵.基于CAE平台的汽车注塑件工艺仿真与质量控制[J].塑料工业,2015,43(5):39-42.
LIN J B.Process Simulation and Quality Control of Auto Injection Molded Parts Based on CAE Platform[J].China Plastics Industry,2015,43(5):39-42.
【6】郭志英,李德群.注塑制品翘曲变形有限元数值模拟的误差分析[J].华中理工大学学报,2000,28(8):63-65.
GUO Z Y,LI D Q.Error Analysis of Finite Element Numerical Simulation in the Warpage of Injection Molded Parts[J].Journal of Huazhong University of Science and Technology,2000,28(8):63-65.
【7】耿铁,李德群,周华民.全三维注塑成形流动模拟有限元模型的研究[J].中国机械工程,2006,17(5):505-509.
GENG T,LI D Q,ZHOU H M.Three-dimensional Finite Element Method for the Filling Simulation of Injection Molding[J].China Mechanical Engineering,2006,17(5):505-509.
【8】ZHANG Y,USMAN M.On the Accuracy of CAE Structural Simulations in Automotive Plastics Component Design[R].SAE,2004-01-0012.
【9】李志刚,贾慧芳,张文亮,等.基于结构谐振CAE分析的注塑机械手优化设计[J].工程设计学报,2013,20(4):293-297.
LI Z G,JIA H F,ZHANG W L,et al.Injection Manipulator Optimization Design Based on the CAE Analysis of Structure Resonance[J].Chinese Journal of Engineering Design,2013,20(4):293-297.
【10】孟兵,徐静,苏艳红,等.“角落效应”对塑料件翘曲变形的影响[J].工程塑料应用,2015,43(7):67-69.
MENG B,XU J,SU Y H,et al.Influence of “Corner Effect”on Deformation of Plastic Part[J].Engineering Plastics Application,2015,43(7):67-69.
【11】田国富,张晓强.汽车转向节强度与多轴疲劳寿命分析[J].机械设计与制造,2015(4):39-43.
TIAN G F,ZHANG X Q.Strength and Multi-axial Fatigue Life Analysis of Automotive Steering Knuckle[J].Machinery Design & Manufacture,2015(4):39-43.
【12】吴晓涛,张建振,李跃伟,等.载货汽车橡胶复合悬架设计[J].汽车技术,2015(2):1-3.
WU X T,ZHANG J Z,LI Y W,et al.Innovative Design of Rubber Composite Suspension for Medium-duty Truck[J].Automobile Technology,2015(2):1-3.
【13】于荣泉,李强,李娜,等.车轮滚动接触疲劳裂纹萌生寿命预测[J].铁道学报,2015,37(12):20-24.
YU R Q,LI Q,LI N,et al.Numerical Analysis on Prediction of Rolling Contact Fatigue Crack Initiation Life of Wheel[J].Journal of the China Railway Society,2015,37(12):20-24.
Study on the Accuracy of CAE Simulation in Automotive Plastic Parts Development
ZHANG Jingqiu, LIU Jianyuan
(Guangdong University of Science & Technology, Dongguan Guangdong 523083,China)
CAE software provides with all the required tools, ranging from analyzing component performance to system level design, and can be used to do so many kinds of automotive simulation research. But the theory of CAE technology leads to that the simulation results are correct only in fitted field. Especially the simulation on the plastic parts performance, which results accuracy should be studied carefully. Main facts, which directly influenced the accuracy of the CAE simulation, were analyzed. Then three carefully selected cases, natural frequency prediction, vibration stress calculation, and fatigue analysis, were studied to illustrate the problem of the accuracy of the CAE simulation results. The first case study demonstrates that CAE is able to achieve great accuracy in predicting structural global properties such as natural frequency. The second case shows that CAE results do not correlate so well for the predictions of local properties such as vibration induced stress or strain response, while the third one indicates that CAE predictions on A to B comparison is always accurate even in the case of fatigue life prediction, that is known as a difficult task. Therefore, the CAE global properly predictions should weigh heavier in plastic component design evaluation than on the local ones. A to B comparison is always preferred whenever the local property prediction is needed, whenever to interpret the CAE stress or strain predictions becomes necessary, extra care has to be exercised to avoid potentially misleading the product design.
Automotive; Plastic; CAE simulation; Accuracy
2016-05-18
张静秋(1979—),男,博士,主要从事动力机械建模、仿真及优化。E-mail:464420763@qq.com。
U465.4+1
A
1674-1986(2016)08-001-06

