差异化隐私预算分配的线性回归分析算法

郑　剑　邹鸿珍

(江西理工大学信息工程学院　江西 赣州 341000)



差异化隐私预算分配的线性回归分析算法

郑剑邹鸿珍

(江西理工大学信息工程学院江西 赣州 341000)

针对用差分隐私方法进行线性回归分析敏感性偏大的问题，提出一种差异化的隐私预算分配算法Diff-LR(DifferentialPrivacyLinearRegression)。该算法首先把目标函数分解成两个子函数，再分别计算两个子函数的敏感性、分配合理的隐私预算，并采用拉普拉斯机制给两个子函数系数添加噪音。然后对子函数进行组合，得到添加噪声后的目标函数，求取最优线性回归模型参数。最后利用差分隐私序列组合特性从理论上证明该算法满足ε-差分隐私。实验结果表明，Diff-LR算法产生的线性回归模型具有很高的预测准确性。

差分隐私线性回归分析敏感性隐私预算

0　引　言

图1　线性回归模型实例

线性回归分析是通过对给定数据集的属性值和预测值的统计整理和分析，找出已知属性和预测值的变化规律，用模型表示这种变化规律，并进行预测和分析。回归分析可应用于企业投资分析、医疗支出预测和机器学习等领域。图1为线性回归的一个实例，根据数据集中某台设备的温度和产量两个属性，找出这两者的线性关系模型，这样就能够利用设备的温度预测出该设备的产量。

在实际应用中，直接发布回归模型参数容易泄露预测函数和数据集的数据信息。为了防止这种隐私泄露，隐私保护就变得非常重要。常用的隐私保护方法有k-anonymity[1]、l-diversity[2]、t-closeness[3]等，但是这些方法大部分都是基于某种背景知识。2006年Dwork[4]提出了差分隐私的理论体系，该模型不论攻击者具有多少背景知识，都能够通过添加噪声的方式，在较高程度上保护数据集隐私的同时尽可能减小数据的失真。文献[5]用差分隐私的方法实现了社会网络数据的发布。文献[6]基于差分隐私对一批线性计数查询提出了一个最优方案。文献[7]提出了一种发布差分隐私直方图的有效方法。文献[8]提出了一种基于遗传算法的多用途差分隐私模型。文献[9-11]总结了各种面向数据发布和分析的隐私保护方法，指出基于差分隐私的回归分析方法，并表明把差分隐私和回归分析进行结合和拓展也是一大研究热点。

应用差分隐私方法设计回归分析的算法中，文献[12]直接在输出结果上添加噪音，在一定程度上保护了隐私，但是所需噪声较大，影响预测精度；文献[13,14]提出了一种逻辑回归分析方法，直接对n个扰动函数的均值添加噪声，添加噪音量有所减少，但该方法通用性不强。

文献[15]提出了一种函数机制FM(FunctionalMechanism)，通过对目标函数的系数统一添加噪声，得到添加噪声后的目标函数，再计算出最优的预测模型参数。该方法通用性强，适用于线性回归和逻辑回归等多种分析方法，但是算法的敏感性偏高，造成添加噪声偏大，使模型预测精度偏低。对于这个问题，本文提出一种针对线性回归分析的差分隐私算Diff-LR。通过对线性回归模型的目标函数进行分解，分配合理的隐私预算，再用拉普拉斯噪声分别对两个子函数的系数进行扰动，降低了整个算法的敏感性，减少了添加的拉普拉斯噪声，使线性回归模型预测更准确。

1　相关理论

1.1相关定义

定义1[4](ε-差分隐私)设有两个数据集D1和D2，D1和D2最多相差一个元组，给定一个随机隐私函数A，Range(A)表示A可能输出结果O的取值范围(O∈Rang(A))，如果A满足下列不等式，则称函数A满足ε-差分隐私。

Pr[A(D1)=O]≤eε×Pr[A(D2)=O]

(1)

其中，ε表示隐私预算的代价，ε越小，数据保护程度越高。

定义2[16]对任意函数f：D→Rd，f的敏感性可定义为：

(2)

其中，D1，D2为给定的数据集，相差至多一条元组。

拉普拉斯机制的主要思想是通过添加拉普拉斯噪声来实现保护隐私的效果。

定理1[16]对于任一函数f：D→Rd，D为数据集，Δf表示其敏感性的大小，那么随机算法：

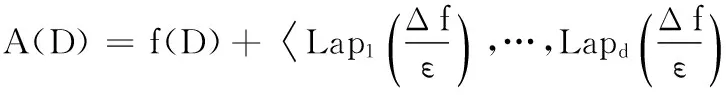
1.2差分隐私组合特性

差分隐私包含两个重要的组合性质[18]，一是序列组合性，二是并行组合性。

性质1[17](序列组合性)给定一个数据集D，任一随机函数Ai满足εi-差分隐私，其中1≤i≤n，则函数Ai构成的组合函数对同一数据集D满足∑εi-差分隐私。

性质2[17](并行组合性)设任一随机函数Ai满足εi-差分隐私，其中1≤i≤n，对于互不相交的数据集Di，则函数Ai(Di)构成的组合函数满足(max(εi))-差分隐私。

1.3问题描述

2　Diff-LR算法设计与分析

2.1Diff-LR算法设计

Diff-LR算法首先对线性回归模型的目标函数进行推导，把它简化成一个简单的二次多项式函数；然后把目标函数分解成两个子函数，计算它们各自的敏感性；对子函数合理分配隐私预算，再分别对两个子函数的系数添加拉普拉斯噪声，得到两个新的子函数，重新组合成一个添加噪声后的目标函数。当该目标函数取最小值时，得到最优的模型参数。

线性回归模型的目标函数可做出如下推导：

(3)

那么，很容易把目标函数看作w的二次函数，可简化为：

fD(w)=aw2+bw+c

(4)

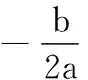
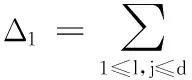
(5)

(6)

对子函数g(w)、t(w)分配隐私预算ε1、ε2，根据拉普拉斯机制的特性可知，拉普拉斯噪音量的大小与函数的敏感性成正比，与隐私预算成反比。为了减少添加的噪声量，当敏感性较大时分配较大的隐私预算，敏感性较小时分配较小的隐私预算。根据计算的Δ1和Δ2的大小可知，敏感性在数据集属性维度d较大时，g(w)的敏感性比t(w)的敏感性更大。因此，分配隐私预算ε1、ε2时，使ε1≥ε2，即对于固定隐私预算ε，通过合理分配ε1、ε2，就可以减少噪音,使线性回归模型预测更准确。

Diff-LR算法如下：

1.ε=ε1+ε2

3.g(w)=aw2，t(w)=bw

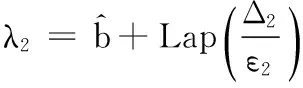
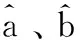
2.2算法分析

基于下面定理的证明，验证算法Diff-LR的正确性。

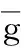
=exp(ε1)

(7)

定理3Diff-LR算法满足ε-差分隐私

Diff-LR算法主要是对线性回归模型的目标函数拆分后的两个子函数分别计算敏感性，分配差异化的隐私预算以及对子函数的系数分别添加噪音，对于随机添加的噪音可能致使系数可能变成负数，造成不存在最优解问题，本文引用了文献[15]提出的正则化和谱修剪方法来避免这种情况。

3　实验设计与分析

文中的实验环境为Win7，3.6GHz，2.00GB，Diff-LR算法是用Matlab语言实现。同FM算法一样，所用数据集US和Brazil都来自IntegratedPublicUseMicrodata[18]，分别包含370 000和190 000条数据集，对数据集中的每个属性值进行预处理，使它们的取值范围在[-1,1]。

本文通过选取数据集条数的80%作为训练集，用来得到线性回归模型，剩下20%为测试集，用来测试该模型的准确性。对实验结果采用的评判标准是均方误差errorRate，定义如下：

(8)

其中，n表示测试集数据元组个数，xi和yi是数据集中已经给出的数据。每条元组的均方误差越小，线性回归模型预测越准确。

分别对数据集US和Brazil进行实验，针对不同数据集，不同的隐私预算ε值，Diff-LR算法和FM算法对实验结果产生影响如图2和图3所示。通过合理分配隐私预算参数ε1、ε2，当隐私预算ε相同时，Diff-LR算法比FM算法均方误差更小，即Diff-LR算法添加噪声后的线性回归模型预测比FM算法更准确。随着ε逐渐增大，Diff-LR算法均方误差errorRate不断接近无噪音预测模型产生的误差，在保护隐私的同时极大降低了数据失真。不论对于较大数据集US还是较小数据集Brazil，Diff-LR算法都比FM算法的errorRate更小。同时，无论隐私预算怎么变化，无噪音模型的均方误差基本不变。

图2　两种算法在数据集US上均方误差errorRate结果比较

图3　两种算法在数据集Brazil上均方误差errorRate结果比较

Diff-LR算法的均方误差比FM算法均方误差更小的原因有两点。1)Diff-LR算法对目标函数进行拆分，使得其中一个子函数的敏感性为4d，另一个子函数的敏感性为2d2，而FM算法的敏感性为2(2d+d2+1)。根据拉普拉斯机制性质可知，拉普拉斯中噪音量的大小与敏感性成正比，算法的敏感性越大所需要的噪声越大。因为FM算法敏感性比Diff-LR算法敏感性更大，所以FM算法添加噪声产生的影响比Diff-LR算法更大，造成Diff-LR算法比FM算法均方误差更小，预测更准确。2)FM算法和Diff-LR算法均满足ε-差分隐私，不同的是，FM算法是把隐私预算ε分配给整个目标函数，而Diff-LR算法通过分别给两个子函数分配不同的隐私预算ε1、ε2，同时保证ε=ε1+ε2。Diff-LR算法为了减少添加的噪声量，给敏感性较大的函数分配较大的隐私预算，给敏感性较小的函数分配较小的隐私预算，即ε1≥ε2，添加的噪声更少，数据失真更小，预测精度更高。

4　结　语

本文提出了一种基于差分隐私的Diff-LR算法，用于针对线性回归模型分析。该算法把目标函数拆分成两个子函数，分别分配合理的隐私预算，通过降低算法敏感性，减少了添加的拉普拉斯噪声量，在满足差分隐私的同时，使线性回归模型预测得更加精确。实验结果表明了针对线性回归分析Diff-LR算法相对于FM算法的优越性。

[1]SweeneyL.K-anonymity:amodelforprotectingprivacy[J].InternationalJournalonUncertainty,FuzzinessandKnowledgeBasedSystems,2002,10(5):557-570.

[2]MachanavajjhalaA,KiferD,GehrkeJ,etal.l-diversity:Privacybeyondk-anonymity[J].ACMTransactionsonKnowledgeDiscoveryfromData,2007,1(1):3.

[3]LiN,LiT,VenkatasubramanianS.t-closeness:Privacybeyondk-anonymityandl-diversity[C]//Proceedingsofthe23rdInternationalConferenceonDataEngineering(ICDE). 2007,7:106-115.

[4]DworkC.Differentialprivacy[M]//Automata,LanguagesandProgramming,SpringBerlinHeidelberg,2006:1-12.

[5]ChenR,AcsG,CastellucciaC.Differentiallyprivatesequentialdatapublicationviavariable-lengthn-grams[C]//Proceedingsofthe2012ACMConferenceonComputerandCommunicationsSecurity(CCS),2012:638-649.

[6]YuanG,ZhangZ,WinslettM,etal.Low-rankmechanism:Optimizingbatchqueriesunderdifferentialprivacy[J].ProceedingsoftheVLDBEndowment,2012,5(11):1352-1363.

[7]XuJ,ZhangZ,XiaoX,etal.Differentiallyprivatehistogrampublication[J].TheInternationalJournalonVeryLargeDataBases,2013,22(6): 797-822.

[8]ZhangJ,XiaoX,YangY,etal.PrivGene:differentiallyprivatemodelfittingusinggeneticalgorithms[C]//Proceedingsofthe2013internationalconferenceonManagementofdata,ACM,2013:665-676.

[9] 张啸剑，孟小峰.面向数据发布和分析的差分隐私保护[J].计算机学报，2014，37(4)：927-949.

[10] 熊平，朱天清，王晓峰．差分隐私保护及其应用[J].计算机学报，2014,37(1)：576-590.

[11] 李扬，温雯，谢光强．差分隐私保护研究综述[J].计算机应用研究，2012，29(9)：3201-3211.

[12]SmithA.Privacy-preservingstatisticalestimationwithoptimalconvergencerate[C]//Proceedingson43thannualACMsymposiumonTheoryofComputing(STOC),ACM,2011:813-822.

[13]ChaudhuriK,MonteleoniC.Privacy-preservinglogisticregression[C]//AdvancesinNeuralInformaationProcessingSystems. 2009: 289-296.

[14]ChaudhuriK,MonteleoniC,SarwateAD.Differentiallyprivateempiricalriskminimization[J].TheJournalofMachineLearningResearch,2011,12: 1069-1109.

[15]ZhangJ,ZhangZ,XiaoX,etal.FunctionalMechanism:Regressionanalysisunderdifferentialprivacy[C]//ProceedingsoftheVLDBEndowment,2012,5(11): 1364-1375.

[16]DworkC,McsherryF,NissimK,etal.Calibratingnoisetosensitivityinprivatedataanalysis[C]//Proceedingsofthe3thTheoryofCryptographyConference(TCC),NewYork,USA,2006: 363-385.

[17]McsherryF.Privacyintegratedqueries:anextensibleplatformforprivacy-preservingdataanalysis[J].CommunicationsoftheACM,2010,53(9): 89-97.

[18]MinnesotaPopulationCenter.Integratedpublicusemicrodataseries-international:Version5.0[OL].[2009].https://international.ipums.org.

LINEARREGRESSIONANALYSISALGORITHMOFDIFFERENTIALPRIVACYBUDGETALLOCATION

ZhengJianZouHongzhen

(School of Information Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China)

Fortheproblemofrelativelybigsensitivitywhenusingdifferentialprivacymethodtomakelinearregressionanalysis,thispaperputsforwardthedifferentialprivacybudgetallocationalgorithm-Diff-LR.First,thealgorithmdividestheobjectivefunctionintotwosub-functions,thencalculatesthesensitivitiesofthemseparatelyandallocatesreasonableprivacybudgettothem,aswellasusesLaplacetransformmechanismtoaddnoisestothecoefficientsofthem.Afterthat,itcombinesthesetwosub-functions,andgetstheobjectivefunctionwiththenoiseadded.Thenitcalculatestheoptimallinearregressionparameters,andfinallyemploysthecharacteristicofdifferentialprivacysequencecombinationtoprovetheoreticallythisalgorithmsatisfiesε-differentialprivacy.ExperimentalresultsshowthatthelinearregressionmodelgeneratedbyDiff-LRhashighpredictiveaccuracy.

DifferentialprivacyLinearregressionanalysisSensitivityPrivacybudget

2014-08-13。江西省教育厅科学技术研究项目(GJJ13415)；江西理工大学科研基金重点课题(NSFJ2014-K11)。郑剑，副教授，主研领域：隐私保护，可信软件。邹鸿珍，硕士生。

TP391

ADOI:10.3969/j.issn.1000-386x.2016.03.065