随机需求下供应链企业订购多Agent协商模型

武玉英　李俊涛　蒋国瑞

(北京工业大学经济与管理学院　北京 100124)



随机需求下供应链企业订购多Agent协商模型

武玉英李俊涛蒋国瑞

(北京工业大学经济与管理学院北京 100124)

针对随机需求下供应链产销订购冲突问题，考虑一个制造商和两个零售商组成的两级供应链，构建主从博弈下的多Agent协商模型。制造商作为博弈主方制定批发价，零售商作为从方选择最优订货量和零售价，制造商Agent和零售商Agent自动协商，运用模拟退火算法寻求模型的最优解。通过算例发现合理的让步策略和收益共享契约能够提高供应链系统利润，实现产销双方的互利共赢。验证模拟退火算法求解该模型比遗传算法能够得到更优解。

协商模型多Agent随机需求主从博弈模拟退火算法遗传算法

0　引　言

近年来，制造业中单个企业无法独自应对复杂的市场竞争和动态的市场需求，纷纷寻求与其供应链的上下游企业结成联盟，加强各节点企业之间的合作，努力在组织、业务流程和信息等方面实现协同，谋求整个链的整体效益最大化，提升核心竞争力。供应链节点企业订购是供应链产销协同的重要活动。市场需求随机变化，导致企业订购活动中生产计划和订购量的冲突日益凸显，这一问题已经引起学者们的重视[1-5]。

目前关于随机需求下供应链产销双方的协同订购博弈研究较多。基于价格折扣、数量折扣、激励契约、批发价契约、收益共享契约的两阶段博弈研究比较成熟。基于数量折扣和价格折扣的两级供应链的博弈，提高了企业的合作效率[2]。准时采购下，基于准时交货激励的供应链博弈研究，促进了企业的及时响应，提高了供应链效率[3]。竞争环境下，供应链产销双方博弈在约束条件下存在纳什均衡解[4]。制造商采取收益共享契约可协调供应链达到集中式供应链的效果，而批发价契约不能达到这种效果[5，6]。供应链网络中的零售商的最优定价随批发价单调递增，随其他零售商的定价单调增加，最优订货量随批发价单调递减[7]。两阶段供应链系统的价值构成研究，揭示了供应链的价值来源[7]。

以上研究主要讨论供应链企业的产销订购策略对供应链协调的影响。对于如何制定最优订购策略使供应链系统最优的研究尚显不足，已有学者通过协商进行此方面的研究，分析了讨价还价博弈协商的一般Nash解[9]和批量订货问题的Nash协商解[10]。但传统的协商方式远不能满足信息时代的需求，于是出现了多Agent协商，多Agent协商具有分布性、交互性和智能性等优势，是解决产销冲突的有效方式[11]，适用于复杂环境的供应链产销协同管理，能够满足企业生产和市场需要[12]。多Agent成员通过协商能够很好地进行动作策略选择和移动，解决实时动态和受限通信对抗环境下的决策和合作问题[13]。本文研究一个制造商和两个零售商组成的两级供应链产销订购问题，通过多Agent协商，探讨产销双方最优批发价、零售价和订货策略，使双方达到共赢，实现随机需求下供应链网络的协调。

1　供应链主从博弈模型

1.1问题描述及参数说明

本文讨论一个制造商S1和两个零售商R1、R2组成的两级供应链主从博弈，只考虑单周期订货问题。制造商根据零售商的订货量进行生产，对所有零售商制定统一的批发价格。零售商制定零售价格和向制造商订货。考虑缺货损失，销售季节末剩余产品做残值处理。零售商的需求为价格敏感性的随机需求，同时受其他零售商定价的影响。定义相关参数如表1所示。

表1　参数符号及含义

1.2主从博弈模型

(1) 需求函数

零售商面临的市场需求[7]可以表示为:

(1)

即同一个制造商提供的产品在不同的零售商处的零售价格对自己和其他零售商的需求都有影响。参数b1j,b1k≥0(k≠j)，其中εj是随机变量，其分布函数为Fj(·)。

(2) 模型假设

对该模型做出如下假设：

假设1制造商和零售商协商成功后，零售商的订单都能实现，制造商完全按照零售商的订单生产，期末无残值。

假设2在单周期内不考虑库存成本。

假设3零售价与单位缺货成本之和大于单位运营成本与残值之和，即p1j+u1j>vj+h1j,j=1,2。

假设4随机需求项εj服从均匀分布，即：

(2)

(3) 零售商和制造商的利润函数

零售商j的利润可以表示为销售收入减去运营费用，减去缺货成本和制造商支付，加上期末剩余产品残值，整理表示如下：

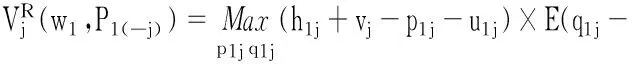
(3)

其中：

制造商1的利润等于从零售商j处得到的转移支付减去其成本，整理如下：

(4)

2　供应链企业订购多Agent协商模型

模拟退火算法通过模拟退火过程，跳过局部收敛，全局寻找最优方案，能够解决供应链系统最优问题[14]。针对上述供应链主从博弈模型，结合多Agent系统的特点，构建供应链企业订购多Agent协商模型，利用制造商Agent、零售商Agent和协商Agent协商批发价，通过模拟算法寻求最优订购策略，实现供应链系统优化。

2.1批发价让步策略

若参数β小于1，则Agent为偏好急切型；若参数β等于1，则Agent为偏好平稳型；若参数β大于1，则Agent为偏好投机型[14]。可以根据实际制造商和零售商的偏好，设置批发价提议的让步参数。

2.2模拟退火算法

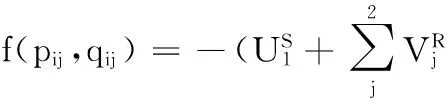
(1) 初始化。初始温度T(0)为100，降温方式采取指数式降温T(n+1)=λT(n)，设置最大迭代次数MAX_ITER，在某一温度下迭代的最大次数MAX_M。

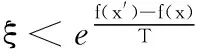
(3) 检查在温度T(n)下是否达到热平衡，这里采用最大迭代次数的检查方式，当在该温度下迭代MAX_M次后，转到第(4)进行降温。否则转到(2)继续迭代。

(4) 进行降温操作：T(n+1)=λT(n)。然后检查算法是否达到最大迭代次数MAX_ITER，如果达到，则算法结束，否则转到(2)进行迭代。

2.3协商流程

图1　协商流程图

初始化协商轮数t=0，协商流程如下：

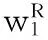
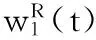
步骤6协商Agent比较t+1是否大于轮数上限TR，若t+1>TR，即超过协商最大轮次，协商失败。否则转入下一步。

3　算　例

考虑一个制造商和两个零售商组成的两级供应链，需求参数如表2所示。先研究批发价契约下的供应链企业协商策略，以制造商为协商发起者，首先提出批发价提议，协商参数如表3所示，对该协商模型进行仿真。

表2需求参数选择

参数值a1142b113b'112.5a1241.75b122.2b'121.8A14B18A215B220

表3协商参数选择

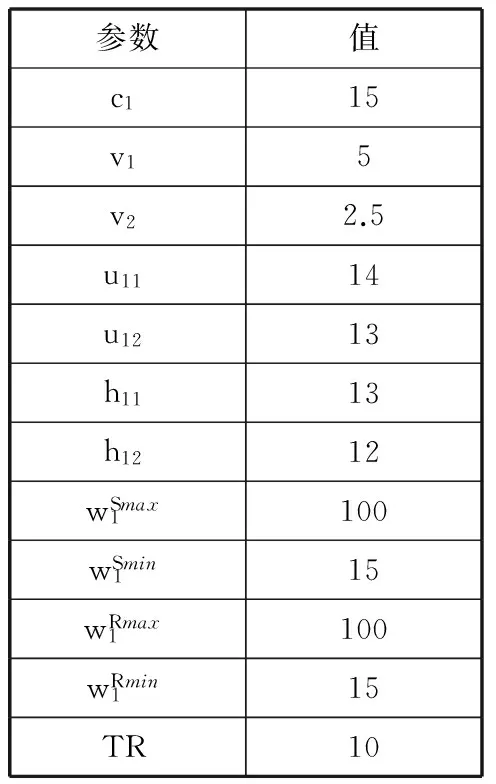
参数值c115v15v22.5u1114u1213h1113h1212wSmax1100wSmin115wRmax1100wRmin115TR10

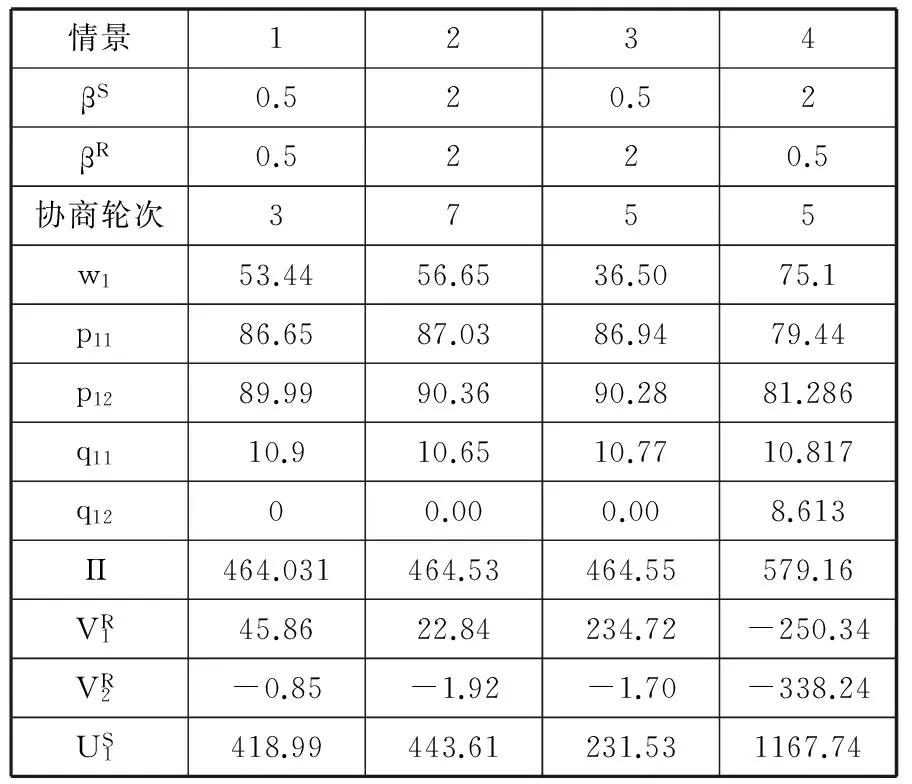
表4　不同让步偏好的多Agent协商结果对比

在收益共享契约下，零售商1、2和制造商按照φ1，φ2，1-φ1-φ2的比例共享供应链系统利润。只有满足以下条件时，博弈双方获得的利润才能都获得比批发价契约下更高的利润。

(5)

遗传算法也是一种智能寻优算法，采用概率化的寻优方法，自适应地调整搜索方向，寻找最优方案。为验证模拟退火算法在本协商模型中的有效性，本文还利用遗传算法求解该协商模型。编制遗传算法主程序Opt_ga.m，同样使用MATLABR2012a最优工具箱中的遗传算法调用主程序Opt_ga.m，求得协商该模型最优解。两种算法求解的最优结果对比如表5所示。对比两种算法下，该协商模型的最优策略和结果，发现运用模拟退火算法的协商模型比遗传算法得到零售商定价更低，销量更高，同时供应链系统利润也增加了。这也恰好印证了经济学原理中的薄利多销理论。

表5　两种算法求解模型最优结果对比

4　结　语

随机需求下，供应链成员中，制造商和零售商之间的订购策略影响着供应链的协调，优化供应链企业订购环节，对于提高供应链运行效率有着重大意义。通过建立基于主从博弈的多Agent协商模型来制定批发价、零售价和订货量，寻找供应链系统最优订货策略。实验发现,采用制定合适的让步策略和收益共享契约可以提高供应链利润，利用模拟退火算法求解该模型寻求供应链系统最优更具有效率，更能提高供应链系统利润，实现供应链的优化和成员的互利共赢。

[1]ScottMC,UdaySK.Competitioninmulti-echelonassemblysupplychains[J].ManagementScience,2005,51(1):45-59.

[2] 王能民，程石磊,冯耕中.基于数量折扣策略的两级供应链协调的博弈分析[J].复旦学报，2007，46(4)：517-522.

[3] 方忠民，陈志亚.基于随机响应时间及准时交货激励的供应链博弈协调模型与算法[J].数学的实践与认识，2013，43(6)：28-34.

[4] 王圣东.基于合作和竞争的供货商与销售商库存模型[J].系统工程学报，2007，22 (1)：98-102.

[5] 徐兵，朱道立.竞争供应链的结构和链内协调策略分析[J].运筹与管理，2008，17(5)：51-57.

[6]MaximeOgier,Van-DatCung,JulienBoissiere，etal.Decentralisedplanningcoordinationwithquantitydiscountcontractinadivergentsupplychain[J].InternationalJournalofProductionResearch,2013,51(9):2776-2789.

[7] 贾俊秀.定制生产下的供应链网络竞争均衡问题研究[J].系统工程学报，2009，24(3)：299-306.

[8] 郝海.随机需求下两阶段供应链的价值构成[J].天津工业大学学报，2011，30(6)：77-80.

[9]JohnCHarsanyi,ReinhardSelten.Ageneralizednashsolutionfortwo-personbargaininggameswithincompleteinformation[J].ManagementScience,1972,18(5-2):80-106.

[10]Bylka,Stanisaw.Non-cooperativestrategiesforproductionandshipmentslotsizinginthevendor-buyersystem[J].ProductionEconomics,2011,131(1):372-382.

[11]LiYingzi,ZhangShuo,ZhangXiaodong,etal.Agent-basedpartnerselectionandsimulationincollaborativeproductdevelopmentprocess[J].AdvancesinInformationSciencesandServiceSciences,2012,20(4):595-604.

[12] 张瀚林，蒋国瑞，黄梯云.一种有限信息共享的全局寻优供应链双边协同计划方法[J].管理工程学报， 2010，24(2)：153-159.

[13] 申静.对抗环境下多Agent协商问题的研究[J].计算机应用与软件，2014，31(1)：165-168.

[14] 陈明.MATLAB神经网络原理与实例精解[M].北京：清华大学出版社，2013.

[15] 董婷婷，冯玉强. 基于辩论的谈判解支持研究[J].预测，2009，28(2)：76-80.

MULTI-AGENTNEGOTIATIONMODELFORSUPPLYCHAINCOMPANIESORDERINGUNDERRANDOMDEMAND

WuYuyingLiJuntaoJiangGuorui

(School of Economics and Management,Beijing University of Technology,Beijing 100124,China)

Fortheproblemoforderingconflictbetweenproductionandmarketingofthesupplychainunderrandomdemand,weconsideredatwo-levelsupplychainconsistingofonemanufacturerandtworetailers,andbuiltthemulti-AgentmodelunderStackelberggame.Asthemainparty,themanufacturerdevelopsthewholesaleprice,andtheretailersasfollowersselecttheoptimalorderquantityandretailprice.ThemanufacturerAgentandtheretailersAgentnegotiateautomaticallyandusesimulatedannealingalgorithmtodiscusstheoptimalsolutionofthemodel.Throughanexample,wefoundthatthereasonableconcessionstrategyandrevenuesharingcontractcouldimprovethesupplychainprofit,realisemutualbenefitsandwin-winprogressbetweentheproductionandmarketing;andthisverifiedthatthesimulatedannealingalgorithmcouldgetbetteroptimalsolutionthangeneticalgorithminsolvingthemodel.

NegotiationmodelMulti-AgentRandomdemandStackelberggameSimulatedannealingalgorithmGeneticalgorithm

2014-09-04。国家自然科学基金项目(71371018)。武玉英，副教授，主研领域：商务智能，系统工程，供应链管理。李俊涛，硕士生。蒋国瑞，教授。

TP181

ADOI:10.3969/j.issn.1000-386x.2016.03.056