基于包含与演绎分析的无冗余序列规则挖掘

周　新　王乙民　刘　婧　尤　涛

1(西安市烟草专卖局　陕西 西安 710061)2(西北工业大学计算机学院　陕西 西安 710129)



基于包含与演绎分析的无冗余序列规则挖掘

周新1,2王乙民1刘婧1尤涛2

1(西安市烟草专卖局陕西 西安 710061)2(西北工业大学计算机学院陕西 西安 710129)

序列规则挖掘旨在发现频繁序列之间的因果关联，当前最优的序列规则产生方法仅考虑两规则间的包含关系而没有考虑多规则间的演绎关系，故而存在大量冗余。引入演绎无冗余规则的概念，分析演绎冗余的原因，重新定义了无冗余规则的概念。在频繁闭序列及其生成子的基础上，基于最大重叠项冗余性检查给出了无冗余规则抽取算法。理论分析和实验评估表明该算法在处理效率基本不变的前提下，提高了序列规则的生成质量。

事件序列规则包含演绎无冗余

0　引　言

随着计算机和因特网技术的迅猛发展，从各种各样应用中收集到的数据量越来越庞大，从海量数据中挖掘出有价值的信息和知识已经成为数据挖掘研究领域中的重要任务之一[1]。序列作为一种重要数据形式，刻画了事件之间的紧随关系，而序列间的因果关联通过序列规则描述。基于序列规则[2]的预测被广泛运用在科学与工程学、商业、客户行为分析、股票趋势预测、DNA 序列分析、Web使用行为分析等领域。但目前的序列规则挖掘算法往往产生大量的多余规则。以最具代表性的包含无冗余规则生成算法Extractor[3]为例，其挖掘结果仍然存在冗余。

我们来看下面的例子：某烟草管理局Web服务器上记载的一条用户对多个品牌香烟的事务记录，ES=。根据这些序列，需要找出该用户的操作行为规则，从而有助于烟草管理局人员发现用户操作之间的关联、非法操作的流程。在支持度阈值minsup=2时，ES上所有的频繁闭序列如表1所示，生成子如表2所示。通过运行算法Extractor在序列ES上发现的所有的包含无冗余序列规则如表3所示。序列规则表达采用五元组的方式给出，例如某规则中，AAB和CD分别是规则的前件和后件，40为支持度，70%是置信度，9为窗口宽度。

表3所列的规则，按照包含无冗余序列规则的定义，已经是最精简的序列规则。但仔细观察不难发现，规则和实际可演绎出规则。导出过程如下：由规则可知AB的支持度为3；由规则可知ABACE的支持度为2。依计算可知，以AB为规则前件、ACE为规则后件的序列规则支持度为2，置信度为67%。因此表3中，为多余规则。

而挖掘结果中的冗余不仅会加大相关应用系统的负担，也不利于工作人员理解，制约工作效率。

据此，本文引入了演绎无冗余规则的概念，提出一种新的无冗余序列规则约简算法SRRM(Sequence rules reduction method)。该算法在传统包含无冗余序列规则的基础上，基于演绎规则约简的方法产生出序列规则的精简集。理论分析和实验评估证明该算法能有效地抽取给定事件序列上的序列规则，与包含无冗余序列规则相比，规则数量平均降低30%左右。

表1　ES上的频繁闭序列

表2　ES上的序列生成子

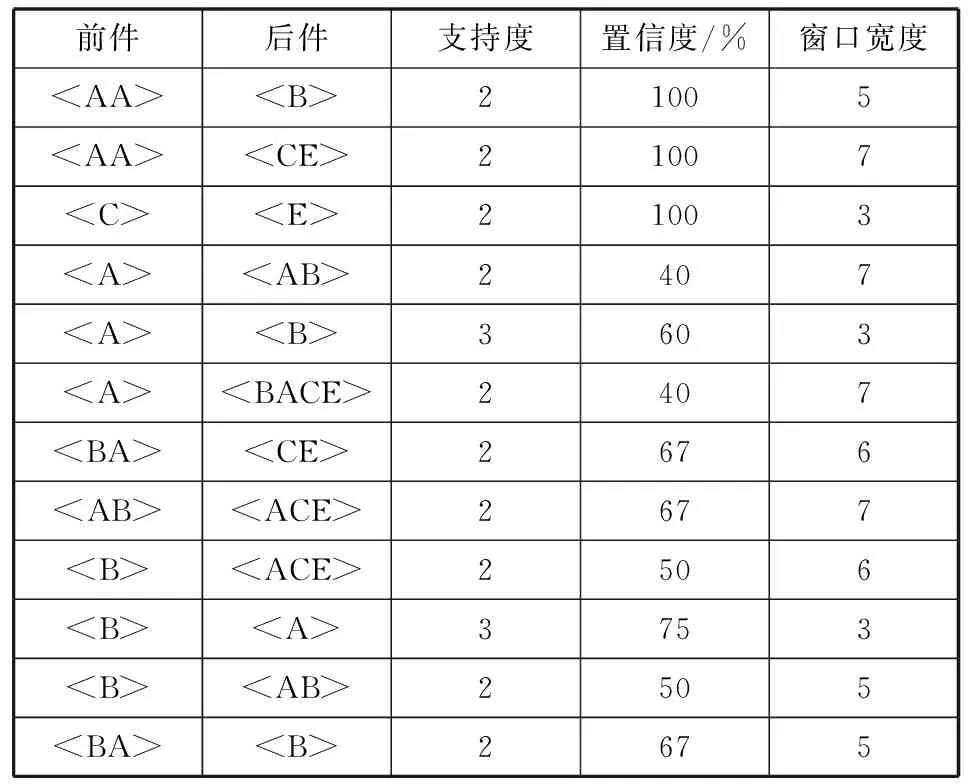
表3　ES上的包含无冗余序列规则

1　研究现状

已有规则挖掘的各类算法，虽然在数据组织、处理流程等方面各有不同，但主要分为三类，如表4所示。

表4　典型序列规则挖掘算法分类比较

产生序列规则全集的典型算法为TASA[4]、WinMiner[5]，该类算法以频繁序列为规则基，通过投影的方式产生序列规则全集。

产生最小前件序列规则全集的典型算法为GenMiner[6]，其规则基为频繁序列与生成子。算法首先采用深度优先的搜索策略来创建存储所有序列的前缀搜索树PSL，然后通过遍历PSL得到包含所有序列模式生成子的超集，据此可以得到最小前件序列规则。

产生包含无冗余序列规则集的典型算法为Extractor[3]，其规则基为频繁闭序列与生成子。算法采用最小且非重叠发生的支持度定义和深度优先的搜索策略来发现频繁闭序列及其生成子；直接由频繁闭序列及其生成子产生序列规则。Extractor算法的规则基——闭序列及其生成子已被证明可产生具有最小前件和最大后件的包含无冗余序列规则[7,8]。

从上述序列规则挖掘算法的发展不难看出，规则的产生方式经历了频繁序列投影、频繁序列及其生成子投影、频繁闭序列及其生成子投影等阶段；算法的效率、精确程度、精简粒度都在逐步提高。但却忽略了多规则间的关联关系在挖掘过程中的作用，造成了引言所述的规则冗余。本文引入的SRRM可有效解决这一问题。

2　SRRM

2.1 相关定义[7]

定义1(事件，事件流)。事件是给定事件类型集ε={E1,E2,…,En}中的事件E和事件发生时间t的二元组(E,t)。事件流是由若干ε中的事件按发生时间先后排列的序列，表示为ES=<(E1,t1),(E2,t2),…,(Es,ts)>。

定义2(序列)。一个序列是由若干事件组成的串，表示为α=<(E1,t1),(E2,t2),…,(Ek,tk)>，简记为α=。

定义4(发生)。给定事件流ES和序列α=，若ES在时间区间[t1,tk]上按α的事件排列顺序出现了α所代表的所有事件，则称ES上发生了序列α，时间区间[t1,tk]称为α在ES上的一次发生。

定义5(支持度)。序列α在事件流ES上所有发生的数目称为α的支持度，记为α·sup。

定义6(频繁序列，频繁闭序列，序列生成子)。给定支持度阈值min_sup，若序列α的支持度大于等于min_sup，则α是一个频繁序列。若序列α是频繁的，且α的支持度不等于α的任何一个真超序列的支持度，则α是一个频繁闭序列。设f是一个闭序列，g⊆f，若g的支持度等于f的支持度，且g不存在与其支持度相同的任何一个真子序列，则g称为闭序列f的一个序列生成子。

定义7(序列规则)。一个序列规则γ是一个五元组(l,r,s,c,ω)。其中γ的前件、后件、支持度、置信度和窗口宽度分别记为l、r、s、c、ω。

定义8给定序列规则γ(l,r,s,c,w)，若不存在序列规则γ′(l,r,s,c,w)，使得γ′·s=γ.s，γ′·c⊆γ·c，γ′·l⊆γ·l，γ′·r⊇γ·r，则称γ是一个包含无冗余序列规则，否则是一个包含冗余序列规则。

2.2演绎规则

可见包含无冗余序列规则是对两规则间包含关系进行的约简。下面我们给出多规则间的演绎关系。

定理1规则演绎。如果规则γ、γ′、γ″之间，满足(1) γ·l=γ′·l或者γ·l=concat(γ′·l,γ′·r)；(2) concat(γ·l,γ·r)=γ″·l或者concat(γ·l,γ·r)=concat(γ″·l,γ″·r)，则γ′∩γ″⟹γ。

证明：γ′·l、concat(γ′·l,γ′·r)的支持度可以由规则γ′得到，而γ·l满足条件(1)，即γ·l的支持度可知；γ″·l、concat(γ″·l,γ″·r)的支持度可以由规则γ″得到，而concat(γ·l,γ·r)满足条件(2)，即concat(γ·l,γ·r)的支持度可知；进而可以计算规则γ的支持度、置信度，确定其窗口宽度。因此γ′∩γ″⟹γ。定理1得证。

由规则间的演绎定理，我们可以得到演绎无冗余规则的概念如下。

定义9给定序列规则γ(l,r,s,c,w)，若不存在序列规则γ′(l,r,s,c,w)、γ″(l,r,s,c,w)，使得(1) γ·l=γ′·l或者γ·l=concat(γ′·l,γ′·r)；(2) concat(γ·l,γ·r)=γ″·l或者concat(γ·l,γ·r)=concat(γ″·l,γ″·r)同时成立。即γ不可以从其他规则产生，则称γ是一个演绎无冗余规则，否则是一个演绎冗余规则。

定理1和定义9分别给出了规则演绎和演绎无冗余规则的最一般描述，对描述进行展开，可以得到规则演绎的各种情况如表5所示。为了不失一般性，我们对表5所示的各种情况分析如下。

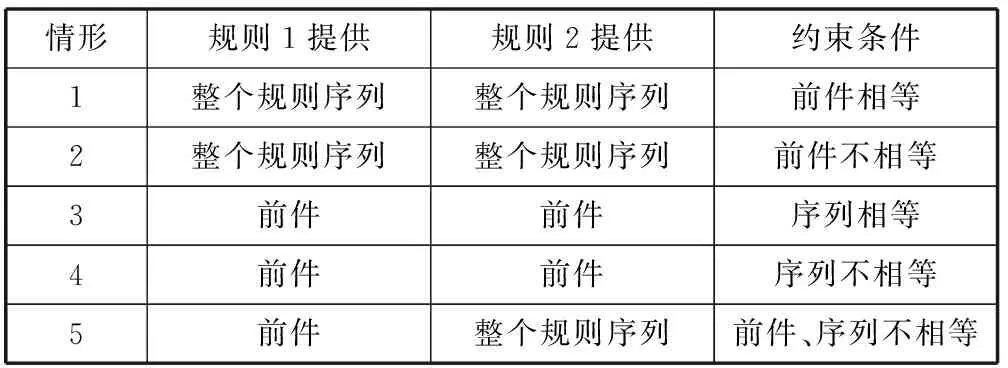
表5　规则演绎的情况分解表

对于情形1来说，已知γ1(l,r,s,c,w)和γ2(l,r,s,c,w)，γ1·l=γ2·l，concat(γ1·l,γ1·r)⊂concat(γ2·l,γ2·r)或concat(γ1·l,γ1·r)⟺concat(γ2·l,γ2·r)，假设concat(γ1·l,γ1·r)⊂concat(γ2·l,γ2·r)则必有concat(γ1·l,γ1·r)->project(concat(γ2·l,γ2·r),concat(γ1·l,γ1·r))，即γ3·l=concat(γ1·l,γ1·r)，γ3·r=project(concat(γ2·l,γ2·r),concat(γ1·l,γ1·r))，而γ3·s=γ2·s，γ3·c=γ2·s/γ1·s，情形1可推导。

对于情形2来说，推导过程与情形1类似，只是增加了γ1·l≠γ2·l的条件，并不影响结论。情形2可推导。

对于情形3来说，已知γ1(l,r,s,c,w)和γ2(l,r,s,c,w)，concat(γ1·l,γ1·r)=concat(γ2·l,γ2·r)，γ1·l⊂γ2·l或γ2·l⊂γ1·l，假设γ1·l⊂γ2·l则必有γ1·l->project(γ2·l,γ1·l)，即γ3·l=γ1·l，γ3·r=project(γ2·l,γ1·l)，而γ3·s=γ2·s/γ2·c，γ3·c=(γ2·s/γ2·c)/(γ1·s/γ1·c)，情形3可推导。

对于情形4来说，推导过程与情形3类似，只是增加了concat(γ1·l,γ1·r)≠concat(γ2·l,γ2·r)的条件，并不影响结论。情形4可推导。

对于情形5来说，已知γ1(l,r,s,c,w)和γ2(l,r,s,c,w)，γ1·l≠γ2·l，concat(γ1·l,γ1·r)≠concat(γ2·l,γ2·r)。γ1·l⊂concat(γ2·l,γ2·r)则必有γ1·l->project(concat(γ2·l,γ2·r),γ1·l)，即γ3·l=γ1·l，γ3·r=project(concat(γ2·l,γ2·r),γ1·l)，而γ3·s=γ2·s，γ3·c=γ2·s/(γ1·s/γ1·c)，情形5可推导。

定义10(无冗余规则)。满足包含无冗余特征和演绎无冗余特征的规则集合称为无冗余规则。可见无冗余规则既避免了两规则间的包含关系，又避免了多规则间的演绎关系。

文献[3]依据频繁闭序列和生成子，按照生成子在闭序列投影的方式，产生了包含无冗余序列规则，而这些规则中蕴含了冗余的演绎规则。如何在包含无冗余序列规则中过滤到冗余的演绎规则呢？直观的看，可以依据定义通过事后检查的方式进行过滤。但是这种事后过滤的方法仍需要遍历整个规则集合，增加了处理的时间。下面我们从规则产生的过程中，分析冗余演绎规则的产生原因，得出其过滤算法。

2.3SRRM算法流程

通过分析包含无冗余序列规则的产生过程可知，生成子向频繁闭序列投影时，对于互相重叠的生成子和闭序列，它们既可作为闭序列被其他生成子投影，又可作为生成子向其他闭序列投影，这造成了冗余演绎规则。

因此在生成规则的过程中，通过检查、过滤机制就可以有效避免冗余演绎规则的产生。但即便如此，由于投影关系的传递性，进行可演绎规则的过滤仍然是复杂的。为了提高演绎规则的过滤效率，我们给出如下定理。

定理2生成子向频繁闭序列投影时，对互相重叠的生成子和闭序列，重叠集内部会存在互相包含关系，这些关系中，只需考虑最大的重叠项进行演绎规则冗余检查即可。

证明：设有生成子g0、g1、g2，g1、g2是重叠集中的元素，并且g0可以投影到g1，g1可以投影到g2。由于投影规则是可传递的，g0也可以投影到g2，记为g0-g1-g2。设有闭序列e，满足g2-e，则有g0-g1-g2-e。根据定理1，对于g0-g1-e而言，g0-e、g1-e两条规则蕴含g0-g1；对于g0-g2-e而言，g0-e、g2-e两条规则蕴含g0-g2；对于g1-g2-e而言，g1-e、g2-e两条规则蕴含g1-g2。可以看出，由g0-g1-e所产生的规则g0-e、g1-e完全包含在g1-g2-e、g0-g2-e所产生的规则中，而g2为重叠集中较大的元素。以此类推，可证明在进行演绎规则冗余检查时，只需要检查重叠集最大元素的投影和被投影情况即可。得证。

依据定理2，生成规则的流程如算法所示。其中，1～13步为找出检查重叠集最大的元素；14～18步找出最大元素的所有投影和被投影元素；19～29步为冗余演绎规则的过滤过程，即最大重叠元素的一次投影和被投影过程中，最多只产生两个规则；30～35步为生成子和闭序列无重叠情况的规则产生。可见，算法依据重叠集的最大元素过滤掉了演绎序列规则，而算法本身产生的就是包含无冗余序列规则，最终产生了无冗余序列规则。

算法Precedure SRRM(Set ee, Set ge)

Input：ee：a set of non-redundant sequences

ge：a set of generatora

Output：result：a set of non-redundant sequence rules

1.Let result = empty

2.Find ge′ in ge which ge′ has the same item in ee

3.For each g1and g2in ge′

4. If g1can project to g2

5. Delete g1in ge′

6. If g2can project to g1

7. Delete g2in ge′

8.Let ge = ge - ge′ //找到闭序列和生成子的公共集合ge并去除ge中的重叠元素

9.Let gee = empty

10.For each g in gee

11. If g can project to one item in ge′

12. gee.add(g)

//找出ge中的可被投影集合gee

13.Let ge = ge -gee

14.Let ee′ = empty

15.For each e in ee

16. If one item in ge′ can project to e

17. ee′.add(e)

//找出ee中的可被ge中元素投影集合

18.Let ee = ee- ee′

19.For each g1in gee and g2in ge′ and e1 in ee′

20. If g1can project to g2and g2can project to e1

21. Let r =project(g1, g2)

22. Let a=contact(g1,r)

23. If a.sup/g.sup>=minconf

24. result.add(g1,r,a.sup,a.sup/g1.sup,a.w)

25. Let r=project(g2, e1)

26. Let a=contact(g2,r)

27. If a.sup/g.sup>=minconf

28. result.add(g2,r,a.sup,a.sup/g2.sup,a.w)

29.For each f in ee and g in ge

30. If g can project to f

31. Let r=project(g,f)

32. Let a=contact(g,r)

33. If a.sup/g.sup>=minconf

34. result.add(g,r,a.sup,a.sup/g.sup,a.w)

35.Return result

经过演绎规则冗余性检查，表3中的规则，，可被删除。

2.4 算法性能分析

设L为事件序列ES的长度，ε为ES中的事件类型集，FE为ES上所有频繁序列组成的集合，则算法SRRM的复杂度分析如下。

时间复杂度：算法首先需要找到生成子集中具有和FE中相同元素的且之间不含前缀包含关系的生成子集gee，其复杂度为O(|FE|*|FE|)，然后需要在FE中分别找到FE可以对gee中元素进行投影的元素集合以及gee可以对FE中元素进行投影的元素集合，其复杂度皆为O(|FE|*|FE|)。此外，规则产生时需要将序列生成子一一投影到所有的频繁闭序列中进行规则产生，所以规则产生过程所需的时间复杂度为O(|FE|*|FE|)。

空间复杂度：由于需要维护所有的规则信息，最坏情况下空间复杂度为O(|FE|*|FE|)。因此空间复杂度为O(|FE|*|FE|)。

可见，相比与当前最优的包含无冗余序列规则挖掘算法Extractor，没有增加任何时空消耗。

3　实　验

3.1实验设计

实验采用来自烟草网络[8]日志数据库的真实数据集，选取一个烟草网站服务器上的2013年第20周的日志数据，该数据包括了456个用户的总计163 514个操作，操作类型有400种。我们选取当前最优的Extractor算法与SRRM对比，程序采用C++实现。实验所在计算机的配置为CPU INTEL E8500 2.93 GHz，RAM 4 GB，Windows XP Professional。

3.2实验结果

实验1规则个数与置信度阈值的关系。设min_sup=10，通过置信度不断变更，得到了两算法在规则产生情况上的对比(如图1所示)。可见，随着置信度阈值的减少，两个算法均发现了更多的序列规则，这是由于置信度阈值越小，将会有更多的规则满足阈值约束。同时，SRRM发现的规则个数少于Extractor。这是因为SRRM产生的是无冗余规则集，Extractor产生的是包含无冗余序列规则集。当置信度为30%时，存在的演绎规则冗余较大，平均下来SRRM得到的规则与Extractor得到的规则相比，下降了近50%。当置信度为70%时，存在的演绎规则冗余小，平均下来SRRM得到的规则与Extractor得到的规则相比，下降了30%左右。

实验2规则个数与支持度阈值的关系。设置信度阈值为50%，通过min_sup不断变更，得到了两算法在规则产生情况上的对比(如图2所示)。可以看出，随着支持度阈值的减少，算法均发现了更多的序列规则，而SRRM发现的规则个数少于Extractor。原因同实验1。

图1　规则个数和置信度阈值关系图　图2　规则个数和支持度阈值关系图

实验3规则个数与序列长度的关系。设min_sup=10，置信度阈值为60%，得到了序列长度对两算法产生规则的影响情况(如图3所示)。可见，随着序列长度的增加(从1天到5天)，算法均发现了更多的序列规则，但SRRM发现的规则个数少于Extractor。原因同实验1。

由于两算法的时空复杂度相同，所以两个算法的执行效率比较，我们只列出各运行时间与置信度阈值的关系，其他情况这里就不再赘述。

实验4运行时间与置信度阈值的关系。设min_sup=10，通过置信度不断变更，得到了两算法运行时间上的对比(如图4所示)。可见，随着置信度阈值的减少，算法的运行时间都线性增加，SRRM执行时间较Extractor略高，这是由于它还需要进行演绎规则检查。

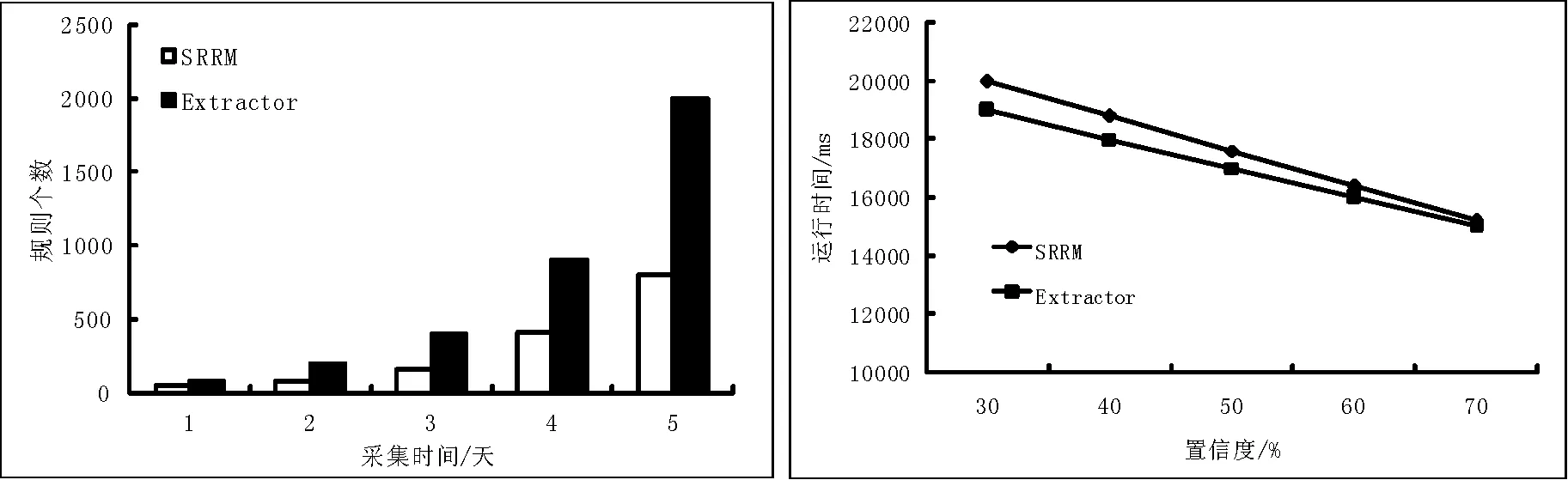
图3　规则个数和序列长度关系图　图4　运行时间和置信度阈值关系图

各实验联合分析，SRRM虽然在处理时间上略有增加，但却将规则个数精简了许多。

4　结　语

针对当前最优的包含无冗余序列规则产生方法没有考虑序列规则间的演绎关系因素，故而存在大量冗余的问题，本文引入了无冗余演绎规则的概念，提出了新的无冗余序列规则概念呢，并给出了无冗余序列规则生成方法。理论分析和实验评估表明该算法能对包含无冗余序列规则进行进一步压缩，提供了更为精简的序列规则。当然，序列规则挖掘只是序列预测的第一步，后续工作我们将研究基于无冗余序列规则的预测方法。

[1] Thiet P T H I.基于前缀树结构的序列模式挖掘算法研究[D].湖南大学,2013.

[2] Sarawagi S,Thomas S,Agrawal R.Integrating association rule mining with relational database systems:Alternatives and implications[C]//Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data,1998:343-354.

[3] 朱辉生,汪卫,施伯乐.基于频繁闭序列及其生成子的无冗余序列规则抽取[J].计算机学报,2012,35(1):53-64.

[4] Hatonen K,Klemettinen M,Mannila H,et al.Knowledge discovery from telecommunication network alarm databases[C]//Proceedings of the 12th IEEE International Conference on Data Engineering.New Orleans,Louisiana,1996:115-122.

[5] Meger N,Rigotti C.Constraint based mining of episode rules and optimal window sizes[C]//Proceedings of the 8th European Conference on Principles and Practice of Knowledge Discovery in Databases.Pisa,Italy,2004:313-324.

[6] Lo D,Khoo S C,Li J.Mining and Ranking Generators of Sequential Patterns[C]//SDM,2008:553-564.

[7] Van Der Aalst W.Process mining:Overview and opportunities[J].ACM Transactions on Management Information Systems (TMIS),2012,3(2):7.

[8] Sarawagi S,Thomas S,Agrawal R.Integrating association rule mining with relational database systems:Alternatives and implications[C]//Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data,1998:343-354.

[9] 王树文,张永伟,郭全中.加快推进中国烟草行业改革研究[J].中国工业经济,2005(2):34-38.

NON-REDUNDANT SEQUENCE RULES MINING BASED ON INCLUSION AND DEDUCTION ANALYSIS

Zhou Xin1,2Wang Yimin1Liu Jing1You Tao2

1(Xi’anTobaccoMonopolyBureau,Xi’an710061,Shaanxi,China)2(SchoolofComputerScience,NorthwesternPolytechnicalUniversity,Xi’an710129,Shaanxi,China)

Sequence rule mining aims at finding the casual association between frequent sequences, current best sequence rules generation approach just considers the inclusion relationship between two rules but does not consider the deduction relationship among multi rules, therefore has lots redundancies. We introduce the concept of deductive non-redundant rules and analyse the reasons for deductive redundancy, as well as redefine the concept of non-redundant rules. We also present the non-redundant sequence rules extraction algorithm based on the maximum overlap term redundancy checking on the basis of frequent closed sequence and its generator. Theoretical analysis and experimental assessment demonstrate that this algorithm improves the generation quality of sequence rules with almost the same efficiency.

EventSequence ruleInclusionDeductionNon-redundant

2014-07-07。国家自然科学基金项目(61303225)。周新，本科，主研领域：数据挖掘，数据流处理。王乙民，本科。刘婧，本科。尤涛，讲师。

TP311.13

A

10.3969/j.issn.1000-386x.2016.03.011