“机车启动”专题分析

◇　山东　刘清发

(作者单位：山东临沂第三十九中学)



“机车启动”专题分析

◇山东刘清发

机车启动问题是功率中的经典题型,现把机车启动的2种方式总结如下．

1　机车以恒定功率启动

1.1启动过程分析

图1

1.2小结

1) 速度-时间图象:机车以恒定的功率启动过程的v-t关系如图2所示.

2) 功率-时间图象:机车以恒定的功率启动过程的P-t关系如图3所示.

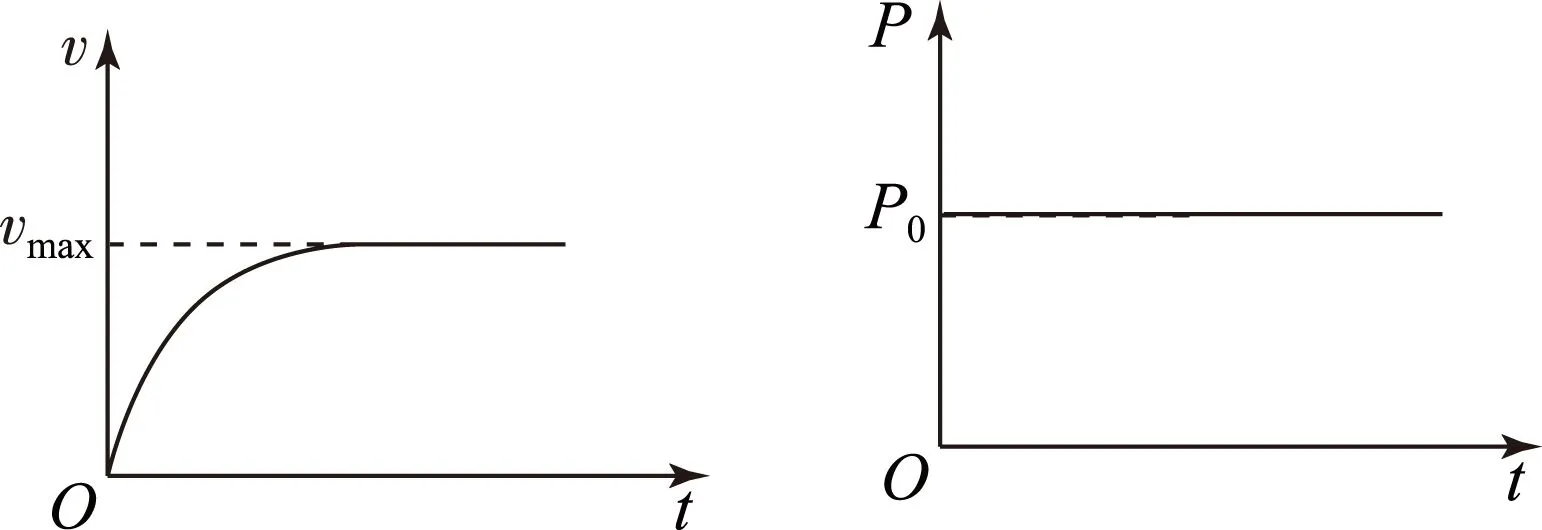
图2　　　　　　　　　图3

图4

(1) 此学生骑车上坡的最大速度是多少?

(2) 假如他在水平路面上骑车,最大速度可达到多少?

答案(1) 2.76 m·s-1; (2) 20 m·s-1.

图5

A320km·h-1;B240km·h-1;

C120km·h-1;D480km·h-1

P=F1v1=k×4mg×v1max,

6节动车加3节拖车编成的动车组满足

6P=F2v2=k×9mg×v2max.

由以上两式得

选项A正确.

答案A.

2　机车以恒定加速度启动

2.1启动过程分析

图6

2.2小结

1)速度-时间图象:机车以恒定加速度启动过程的v-t关系如图7所示.

2)功率-时间图象:机车以恒定加速度启动过程的P-t关系如图8所示.

图7　　　　　　　　　图8

(1) 若汽车以a=0.4m·s-2的恒定加速度启动,则这一过程能维持多长时间?

(2) 汽车在额定功率下行驶,速度为v1=20m·s-1时的加速度.

F=Ff+ma=(800+2×103×0.4)N=

1.6×103N.

保持匀加速运动所能达到的最大速度

这一过程所能维持的时间

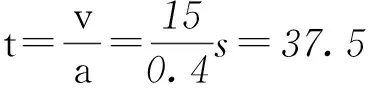
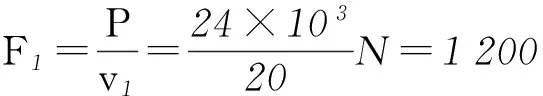
根据牛顿第二定律可知此时加速度

答案(1) 37.5 s. (2) 0.2 m·s-2.

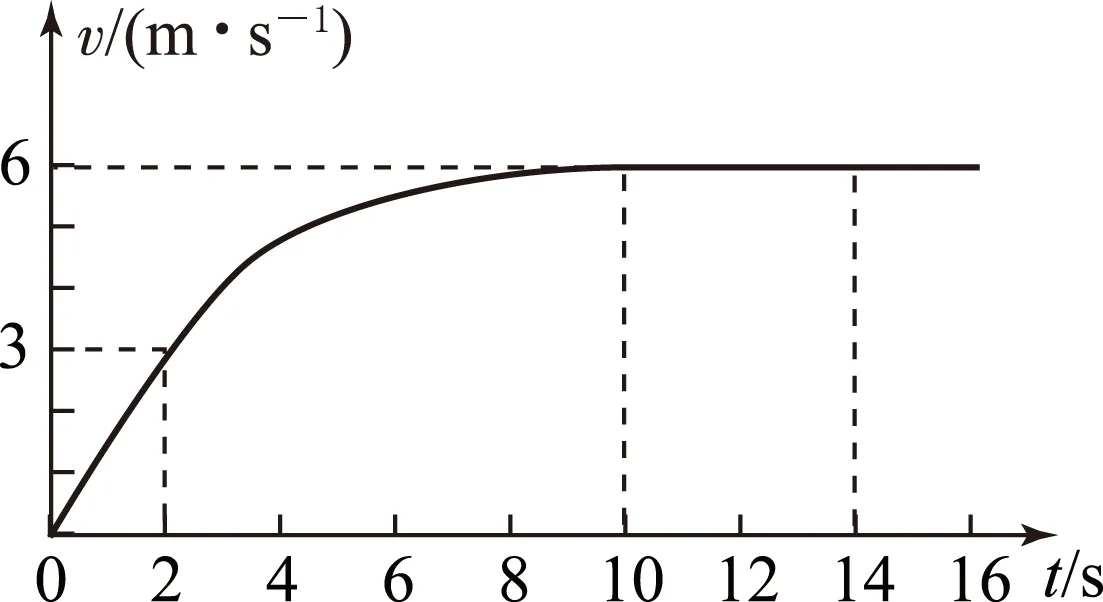
图9

(1) 小车所受到的阻力大小;

(2) 小车在0～10s内位移的大小.

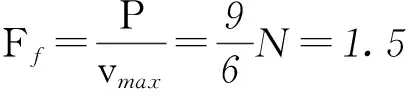
(2) 由图9可以看出小车前2s做匀加速直线运动,设位移为x1,由运动学公式可知

设2～10s时间为t2，位移为x2,由动能定理可知得

解得x2=39m，所以小车在0～10s内位移的大小为

x=x1+x2=42m.

答案(1) 1.5 N; (2) 42 m.

(作者单位：山东临沂第三十九中学)