A STABILIZED MIXED FINITE ELEMENT FORMULATION FOR THE NON-STATIONARY INCOMPRESSIBLE BOUSSINESQ EQUATIONS∗
Zhendong LUO(罗振东)
School of Mathematics and Physics,North China Electric Power University,Beijing 102206,China
E-mail∶zhdluo@163.com;zhdluo@ncepu.edu.cn
A STABILIZED MIXED FINITE ELEMENT FORMULATION FOR THE NON-STATIONARY INCOMPRESSIBLE BOUSSINESQ EQUATIONS∗
Zhendong LUO(罗振东)
School of Mathematics and Physics,North China Electric Power University,Beijing 102206,China
E-mail∶zhdluo@163.com;zhdluo@ncepu.edu.cn
In this study,we employ mixed finite element(MFE)method,two local Gauss integrals,and parameter-free to establish a stabilized MFE formulation for the non-stationary incompressible Boussinesq equations.We also provide the theoretical analysis of the existence,uniqueness,stability,and convergence of the stabilized MFE solutions for the stabilized MFE formulation.
Stabilized mixed finite element formulation;non-stationary incompressible Boussinesq equations;the existence,uniqueness,stability,and convergence
2010 MR Subject Classification65N30;56M15;65M60
1 Introduction
The non-stationary incompressible Boussinesq equations are a nonlinear system of partial differential equations(PDEs)including the velocity vector field and the pressure field as well as the temperature field(see[1-3]),which are named as the non-stationary conduction-convection problem and may be denoted by the following nonlinear system of PDEs.
Problem IFind u=(u1,u2)τ,p,and T such that,for tN>0,

where Ω⊂R2is a bounded and connected domain,u=(u1,u2)τrepresents the fluid velocity vector,p the pressure,T the temperature,tNthe total time,j=(0,1)τthe unit vector,Re the Reynolds number,Pr the Prandtl number√,and u0(x,y,t),u0(x,y),ϕ(x,y,t),and ψ(x,y)are given functions.For the sake of convenience and withoutloss of generality,we may as well suppose that u0(x,y,t)=u0(x,y)=0 and ϕ(x,y,t)=0 in the following theoretical analysis.
There are usually no analytical solutions for the non-stationary incompressible Boussinesq equations because they are a system of nonlinear PDEs including the velocity vector field and the pressure field as well as the temperature field.We have to depend on numerical solutions(for example,see[2-6]).However,most of the existing articles use either the finite difference(FD)schemes or usual mixed finite element(MFE)methods as discretization tools(see[2-6]). To the best of our knowledge,there is not any report employing MFE method,two local Gauss integrals,and parameter-free to establish a stabilized MFE formulation for the non-stationary incompressible Boussinesq equations.Though a stabilized finite element method for the nonstationary Navier-Stokes problem has been presented in[7],the non-stationary incompressible Boussinesq equations include a nonlinear energy equation of the temperature field with the velocity vector field coupled,which are more complex than the non-stationary Navier-Stokes equations without energy equation in[7].Therefore,the study of the stabilized MFE method for the non-stationary incompressible Boussinesq equations has far more difficulties and more challenging,but more important and more serviceable than those for the non-stationary Navier-Stokes equations.Thereby,it is the improvement and innovation for the existing methods(for example,see[3-7]or others).
The remainder of this article is organized as follows.In Section 2,we first review the semidiscrete formulation with respect to time for the non-stationary incompressible Boussinesq equations,and then,we directly establish the stabilized MFE formulation based on two local Gauss integrals and parameter-free from the semi-discrete formulation with respect to time. Thus,we can not only avoid the discussion for semi-discrete stabilized MFE method with respect to spatial variables,but can also evade the constraint of Brezzi-Babuˇska(B-B)condition such that our theoretical analysis becomes simpler than the existing other methods(for example,see[3-7]).In Section 3,we provide the theoretical analysis of the existence,uniqueness,stability,and convergence of the stabilized MFE solutions.Section 4 provides main conclusions.
2 Review Semi-discrete Formulation About Time and Establish Stabilized MFE Formulation
2.1Review semi-discrete formulation about time
The Sobolev spaces along with their properties used in this context are standard(see[8]). Let X=H10(Ω)2,M=L20(Ω)=?q∈L2(Ω);RΩqdxdy=0?,and W=H10(Ω).Thus,a mixed variational formulation for Problem I is written as follows.
Problem IIFind(u,p,T)∈H1(0,tN;X)2×L2(0,tN;M)×H1(0,tN;W)such that,for almost all t∈(0,tN),

where(·,·)denotes inner product in L2(Ω)2or L2(Ω)and

We have the following properties for the above trilinear forms a1(·,·,·)and a2(·,·,·)(see[3-7]):

We have the following properties for the above bilinear forms a(·,·),d(·,·),and b(·,·)(also see[3-7]):

where β is a constant.Define

We have the following known results for Problem II(see[3-6]).
Theorem 2.1If ψ∈L2(Ω),then the problem II has at least a solution which,in addition,is unique provided thatand we have the following prior estimates

Let N be the positive integer,k=tN/N denote the time step increment,tn=nk(0≤n≤N),and(un,pn,Tn)be the semi-discrete approximation of(u(t),p,T)at tn=nk(n= 0,1,···,N)about time.If the differential quotients utand Ttin Problem II at time t=tnare,respectively,approximated by means of the backward difference quotientsand¯∂tTn=(Tn−Tn−1)/k,then the semi-discrete scheme for Problem II with respect to time is written as follows.
Problem IIIFind(un,pn,Tn)∈X×M×W(1≤n≤N)such that

The following existence,stabilization,and convergence of the solution for Problem III are provided in[9].
Theorem 2.2Under the assumptions of Theorem 2.1,Problem III has a unique series of solutions(un,pn,Tn)∈X×M×W(n=1,2,···,N)such that

where C used next is a constant independent of k,but dependent on ψ and known data.And if(u,p,T)∈[H10(Ω)∩H2(Ω)]2×[H1(Ω)∩M]×[H10(Ω)∩H2(Ω)]is the exact solution for the problem I,there hold the following error estimates:

2.2Establish fully discrete stabilized MFE formulation
In the following,we directly establish the fully discrete stabilized MFE formulation based on two local Gauss integrals and parameter-free from the semi-discrete formulation about time.
Let ℑh={K}be the quasi-uniform triangulation of Ω(see[3,10-12]).Finite element subspaces are defined as follows:

where P1(K)is the linear function space on K.
The following lemma is known and useful(see[3,10-12]).
Lemma 2.3Let Ph:X→Xhbe a Ritz-projection,namely,for any u∈X,there exists a unique Phu∈Xhsuch that
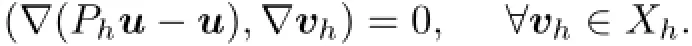
Then,we have the following error estimates

where C in this context indicates a positive constant which is possibly different at different occurrences,being independent of the spatial mesh size h and temporal mesh size k.
Let Qh:M→Mhbe a L2-projection,namely,for any q∈M,there exists a unique Qhq∈Mhsuch that

If q∈Hl(Ω),we have the following error estimates

Let Rh:W→Whbe a Ritz-projection,namely,for any T∈W,there exists a unique RhT∈Whsuch that

Then,we have the following error estimates

Then,the fully discrete stabilized MFE formulation based on two local Gauss integrals and parameter-free is established as follows.


here ε is a positive real number andK,ig(x,y)dxdy(i=1,2)indicate the appropriate Gauss integrals over K which are exact for polynomials of degree i(i=1,2)and g(x,y)=phqhis a polynomial of degree not more than i(i=1,2).
Thus,for all test functions qh∈Mh,the trial function ph∈Mhmust be piecewise constant when i=1.Furthermore,we define the L2−projection operator:L2(Ω)→ˆWhsuch that∀p∈L2(Ω)satisfying

whereˆWh⊂L2(Ω)denotes the piecewise constant space associated with ℑh,the projection operatorhas the following properties(see[3,10-13]):


3 Existence,Uniqueness,Stability,and Convergence of Stabilized MFE Solutions
3.1Existence,uniqueness,and stability of the solutions for Problem IV
In the following,we first devote to proving the existence,uniqueness,and stability of the solutions for Problem IV.We have the following result.
Theorem 3.1Under the hypotheses of Theorems 2.1 and 2.2,there exists a unique series of solutions)(n=1,2,···,N)for the stabilized MFE formulation,namely,Problem IV that satisfies

which shows that the series of the stabilized MFE solutions of Problem IV is stable.
ProofIf(3.1)holds,then when ψ=0,there hold only(n=1,2,···,N).Therefore,Problem IV has a unique series of solutionsXh×Mh×Wh.Thus,we first devote to proving that(3.1)holds.



By summing(3.5)from 1 to n and simplifying,we obtain

By extracting square root for(3.6)and using,we obtain

Using Hüolder inequality and Cauchy inequality,from(3.3),we obtain

By summing(3.8)from 1 to n,extracting square root,using,and simplifying,we obtain

Noting that‖·‖−1≤C‖·‖0,from(3.9)and(3.7),we obtain

Combining(3.9)with(3.10)yields(3.1).If pnh=0,(3.1)is obviously correct,which completes the proof of Theorem 3.2.
3.2The convergence of the solutions for Problem IV
We have the following result about the convergence of the solutions for Problem IV.
Theorem 3.2Under the hypotheses of Theorem 3.1,if(u,p,T)is the solution for Problem IIwe have the following error estimates

ProofBy subtracting Problem IV from Problem III,taking v=vh,q=qh,and φ=φh,we obtain the following system of error equations:



And then,as‖·‖0≤C‖∇·‖0in(Ω),by Hüolder inequality and Cauchy inequality,we have

If ηn6=0,it is easily known thatfrom(2.18).Therefore,there is a constant δ∈(0,1)such thatIf k=O(h),by taking ε=(1−δ)−1,combining(3.16)and(3.17)with(3.15),and using Lemma 2.3,we obtain
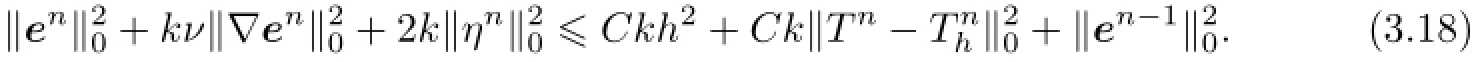
By summing(3.18)from 1 to n,noting that kand simplifying,we have

By extracting square root for(3.19)and using,and then,by simplifying,we obtain

Let Fn=Tn−RhTnand En=RhTn−Tnh.On the one hand,using the error equation(3.14)and Lemma 2.3,we obtain


If k=O(h),by combining(3.21)with(3.22)and using Lemma 2.3,we obtain

By summing(3.23)from 1 to n and using Lemma 2.3,we obtain

By extracting square root for(3.24)and using,we obtain

By using triangle inequality,(3.25),and Lemma 2.3,we obtain

Combining(3.26)with(3.20)and using Lemma 3.3 yield that

Combining(3.26)and(3.27)with Theorem 2.2 yields(3.11).If ηn=0,(3.11)is obviously correct,which completes the proof of Theorem 3.2.
4 Conclusions
In this study,we employ MFE method,two local Gauss integrals,and parameter-free to establish the stabilized MFE formulation directly from the semi-discrete formulation with respect to time for the non-stationary incompressible Boussinesq equations.Thus,we can not only avoid the discussion for semi-discrete stabilized MFE method with respect to spatial variables,but can also evade the constraint of Brezzi-Babuˇska(B-B)condition such that our theoretical analysis becomes simpler than the existing other methods(for example,see[3-7]). We also provide the theoretical analysis of the existence,uniqueness,stability,and convergence of the stabilized MFE solutions.Therefore,the idea and method in this article are new and are the improvement for the existing works(for example,see[3-7]).
References
[1]Wu J H.The 2D Incompressible Boussinesq Equations.Beijing:Peking University Summer School Lecture Notes,July 23-August 3,2012
[2]Wang C,Liu J G,Johnston H.Analysis of a fourth order finite difference method for the incompressible Boussinesq equations.Numerische Mathematik,2004,97(3):555-594
[3]Luo Z D.Mixed Finite Element Methods and Applications.Beijing:Chinese Science Press,2006
[4]Luo Z D.The mixed finite element method for the non stationary Conduction-convection problems.C J Numer Math&Appl,1998,20(2):29-59
[5]Luo Z D,Wang L H.Nonlinear Galerkin mixed element methods for the non stationary conductionconvection problems(I):The continuous-time case.C J Numer Math&Appl,1998,20(4):71-94
[6]Luo Z D,Wang L H.Nonlinear Galerkin mixed element methods for The non stationary conductionconvection problems(II):The backward one-Euler fully discrete format.C J Numer Math&Appl,1999,21(1):86-105
[7]He Y,Lin Y,Sun W.Stabilized finite element method for the non-stationary Navier-Stokes problem. Discrete and Continuous Dynamical Systems B,2006,6(1):41-68
[8]Adams R A.Sobolev Spaces.New York:Academic Press,1975
[9]Luo Z D,Li H,Sun P.A fully discrete stabilized mixed finite volume element formulation for the nonstationary conduction-convection problem.Journal of Mathematical Analysis and Applications,2013,44(1):71-85
[10]Ciarlet P G.The Finite Element Method for Elliptic Problems.North-Holland:Amsterdam,1978
[11]Brezzi F,Fortin M.Mixed and Hybrid Finite Element Methods.New York:Springer-Verlag,1991
[12]Girault V,Raviart P A.Finite Element Methods for Navier-Stokes Equations:Theory and Algorithms. Berlin Heidelberg:Springer-Verlag,1986
[13]Li S,Hou Y.A fully discrete stabilized finite element method for the time-dependent Navier-Stokes equations.Applied Mathematics and Computation,2009,215(1):58-99
February 8,2014;revised April 18,2015.Research of this work was mainly supported by the National Science Foundation of China(11271127)and Science Research Project of Guizhou Province Education Department(QJHKYZ[2013]207).
 Acta Mathematica Scientia(English Series)2016年2期
Acta Mathematica Scientia(English Series)2016年2期
- Acta Mathematica Scientia(English Series)的其它文章
- MEAN-FIELD LIMIT OF BOSE-EINSTEIN CONDENSATES WITH ATTRACTIVE INTERACTIONS IN R2∗
- DIFFERENTIAL OPERATORS OF INFINITE ORDER IN THE SPACE OF RAPIDLY DECREASING SEQUENCES∗
- A BINARY INFINITESIMAL FORM OF TEICHMUüLLER METRIC AND ANGLES IN AN ASYMPTOTIC TEICHMUüLLER SPACE∗
- FAST ALGORITHM FOR CALDER´ON-ZYGMUND OPERATORS:CONVERGENCE SPEED AND ROUGH KERNEL∗
- WEAK TYPE INEQUALITY FOR THE MAXIMAL OPERATOR OF WALSH-KACZMARZ-MARCINKIEWICZ MEANS∗
- ON THE CAUCHY PROBLEM OF A COHERENTLY COUPLED SCHRüODINGER SYSTEM∗
