MEAN-FIELD LIMIT OF BOSE-EINSTEIN CONDENSATES WITH ATTRACTIVE INTERACTIONS IN R2∗
Yujin GUO(郭玉劲)
Wuhan Institute of Physics and Mathematics,Chinese Academy of Sciences,Wuhan 430071,China
E-mail∶yjguo@wipm.ac.cn
Lu LU(陆路)
School of Statistics and Mathematics,Zhongnan University of Economics and Law,Wuhan 430073,China
E-mail∶lulu@znufe.edu.cn
MEAN-FIELD LIMIT OF BOSE-EINSTEIN CONDENSATES WITH ATTRACTIVE INTERACTIONS IN R2∗
Yujin GUO(郭玉劲)
Wuhan Institute of Physics and Mathematics,Chinese Academy of Sciences,Wuhan 430071,China
E-mail∶yjguo@wipm.ac.cn
Lu LU(陆路)
School of Statistics and Mathematics,Zhongnan University of Economics and Law,Wuhan 430073,China
E-mail∶lulu@znufe.edu.cn
Starting with the many-body Schrüodinger Hamiltonian in R2,we prove that the ground state energy of a two-dimensional interacting Bose gas with the pairwise attractive interaction approaches to the minimum of the Gross-Pitaevskii energy functional in the meanfield regime,as the particle number N→∞and however the scattering length κ→0.By fixing N|κ|,this leads to the mean-field approximation of Bose-Einstein condensates with attractive interactions in R2.
Bose-Einstein condensation;attractive interactions;Gross-Pitaevskii functional;mean-field approximation
2010 MR Subject Classification35Q40;46N50;82D50
1 Introduction
As the experimental realization of Bose-Einstein condensates(BEC)in 1995(cf.[1,9]),BEC has been investigated intensively over the past few years.The forces between the atoms in BEC can be either attractive or repulsive.In contrast to the repulsive case,the system of the attractive case collapses if the particle number increases beyond a critical value,seeing,for example,[15,17,18,30]or[8,Sec.III.B],which gives the existence of a critical particle number for cold atoms.The repulsive case has been analyzed widely over the past few years;see,for example,[21,23-25]and references therein.In view of this fact,we shall focus on the attractive case in this article.
As illustrated in[4,8,11,30]and therein,BEC with attractive interactions in two dimensions can be described by the following constraint minimization problem
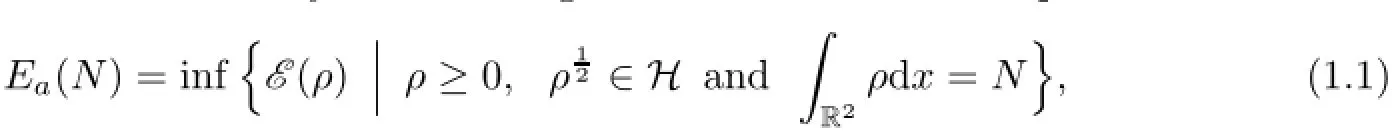
where N>0 denotes the particle number of cold atoms,and the Gross-Pitaevskii(GP)energy functional ε(ρ)is of the form


and from the physical point of view,the trapping potential V(x)is assumed to satisfy
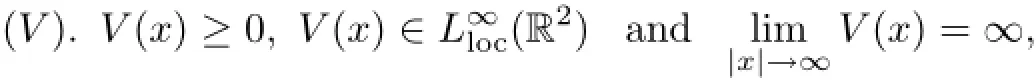
so that H is defined as

Alternatively,it is convenient to consider the L2-normalized minimization problem

where the GP energy functional ε(ρ)satisfies

and the physical constant a>0 is the same as that of(1.2).One can then check that for
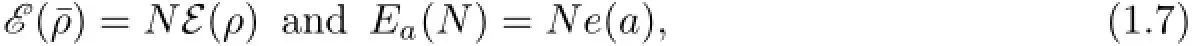
which implies that the analysis of Ea(N)and e(a)can be reduced to each other.
The analytic properties of e(a)(and equivalently of Ea(N))were studied recently in[15,16]. It actually turns out that the problem e(a)is related closely to the following nonlinear scalar field equation

Remark from[13,19,20]that,up to translations,(1.8)admits a unique positive radially symmetric solution,which we denote Q=Q(|x|).Note also from[13,Prop.4.1]that Q(|x|)has the following exponential decay,

Moreover,we recall from[29]the following Gagliardo-Nirenberg inequality
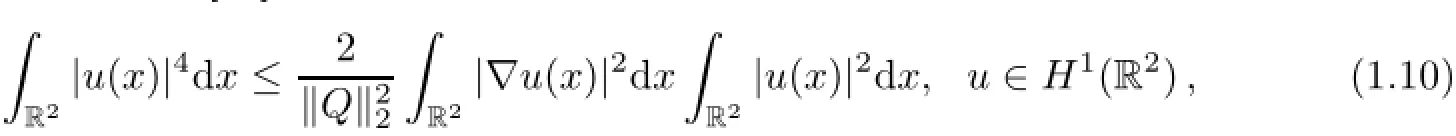
1From the physical point of view,the scattering length κ of attractive BEC is negative.Here,we use κ>0 for convenience.
where the equality is achieved at u(x)=Q(|x|).Also,one can derive from(1.8)and(1.10)that Q(|x|)satisfies
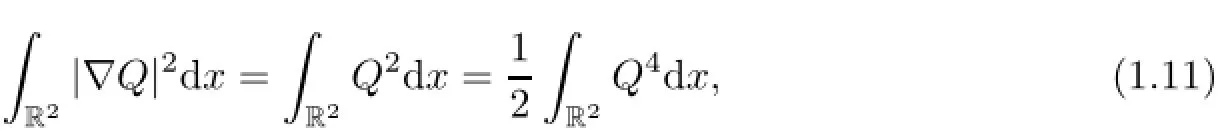
seeing also Lemma 8.1.2 in[6]for more details.
Guo and Seiringer proved recently in Theorem 1 of[15]that e(a)admits minimizers if and only if the constant a>0 satisfieswheredenotes the unique positive radially symmetric solution of(1.8).It follows from(1.3)that the parameter a>0 in e(a)is interpreted as the particle number N times the interaction strength κ.Therefore,the existence of the threshold a∗described in Theorem 1 of[15]yields the existence of a critical particle number for the collapse of attractive BEC[8].Furthermore,the mass concentration and symmetry breaking of minimizers ρ of e(a),as a>0 approaches the critical value a∗from below,were also investigated in[15,16],where all the mass of ρ concentrates at a global minimum of the trapping potential V(x).In contrast,it was analyzed in[21,23-25]that in the case of repulsive interactions(corresponding to the case a<0),the associated GP energy can be derived rigorously from the quantum many-body problem in a suitable low-density limit. In spite of these facts,such a rigorous derivation however remains open in the attractive case a>0.
The main purpose of this article is to address the above open question in the attractive case,and we shall derive that the ground state energy of a two-dimensional interacting Bose gas with the pairwise attractive interaction approaches to the minimum Ea(N)of the Gross-Pitaevskii energy functional in the mean-field regime,as the particle number N of cold atoms is large sufficiently and however a:=Nκ>0 is less than a critical constant,where κ denotes as before the scattering length.Towards this aim,stimulated by[2,3,10,12,14,21,23,24,26,28]and references therein,we start with the quantum system of N particles Hamiltonian in a trap V(·)with the pair interaction w∈N,
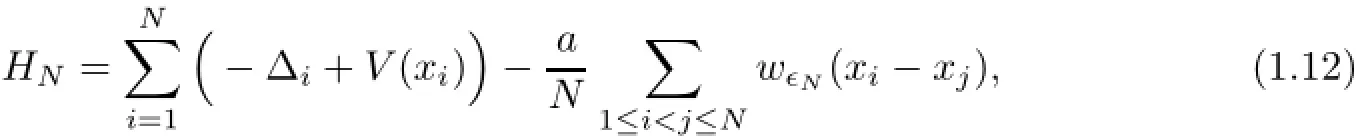
which acts on totally symmetric wave functions in the Hilbert space
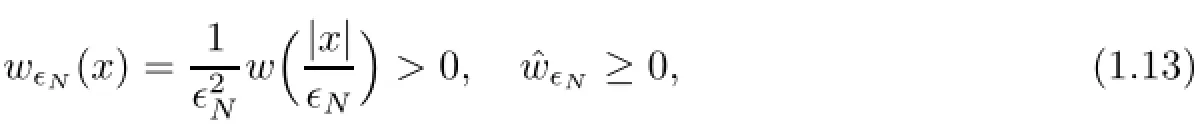


Theorem 1.1Let ǫN>0 satisfy(1.14)with,and denote a:=Nκ>0.Ifthen

If a>a∗,then
We remark that Theorem 1.1 leads to the mean-field approximation of BEC with attractive interactions in R2by fixing a:=Nκ>0.In our choice of the many-body Hamiltonian HN,we however need to neglect the exchange and correlation effects of cold atoms.Therefore,if the exchange and correlation effects of cold atoms are considered,a more complicated Hamiltonian HNis needed.
The remainder of this article is devoted to the proof of Theorem 1.1.
2 Proof of Theorem 1.1
In order to prove Theorem 1.1,as in[26]we justify the mean-field approximation as follows. As in the introduction,we consider the quantum system HNdefined by(1.12)of N particles Hamiltonian in a trap V(·),where the pair interaction w∈Nsatisfies(1.13)and ǫN>0 is as in(1.14).Define as before by(1.15)the above quantum system's quantum energy EQ(N).Note that the quantity EQ(N)can be related to the semiclassical energy functional ε(ρ)defined by(1.2),where the associated GP energy Ea(N)satisfies(1.1).Note also that

which is an easy consequence of the transformation ρ(x)→t−1ρ(x).It is next convenient to introduce some normalized quantities

so that for¯ρ(x)=Nρ(x),

These imply that Ea(N)and e(a)can be reduced to each other.
To address the proof of Theorem 1.1,we first use Ea(N)to derive the upper bound of EQ(N)for the case where adefine the normalized variational function
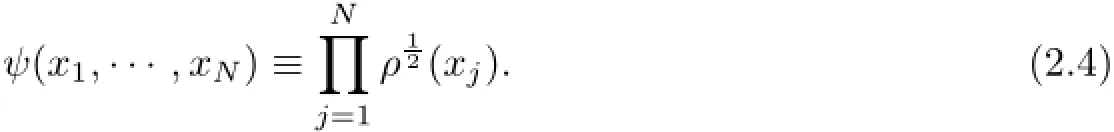
Applying Theorem 4.22 in[5]on the analytic properties of standard mollifiers,we have for i=1,···,N and i 6=j,
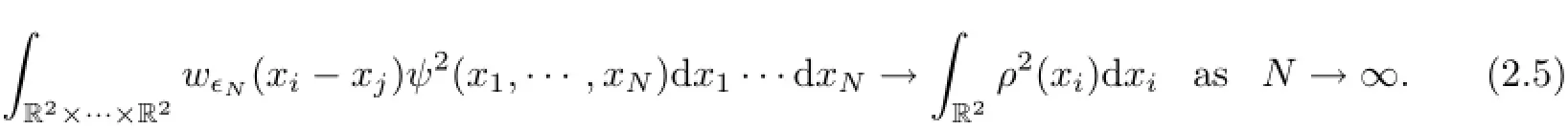
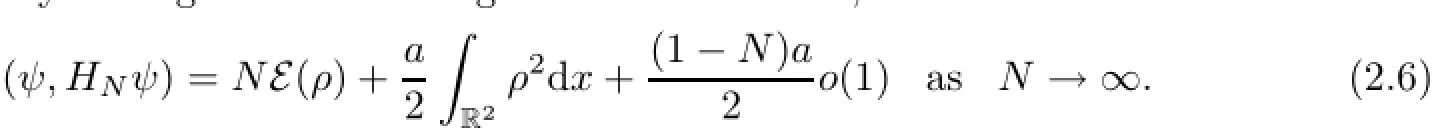
We then obtain by adding and subtracting the self interaction,Recall from Theorem 1 in[15]that if a<a∗,e(a)>0 and there exists at least one minimizer for e(a).In this case,choose ρ to be a minimizer for e(a)and use the Gagliardo-Nirenberg inequality(1.10).We then derive from(2.6)that for all a<a∗,
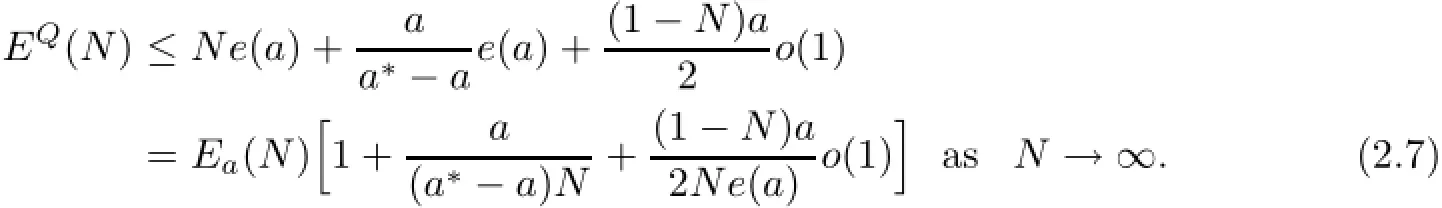
We therefore obtain the upper bound of EQ(N)for the case where a<a∗.
We next use Ea(N)to derive the lower bound of EQ(N)for the case where a<a∗.For this purpose,we denote X={x1,···,xN},and let P be a partition of{1,···,N}into two disjoint sets π1and π2of sizes L and M,respectively,where L+M=N.Note that there aresuch partitions.Rewrite the operator HNas

where the terms hPare given in terms of two positive parameters e and¯a as
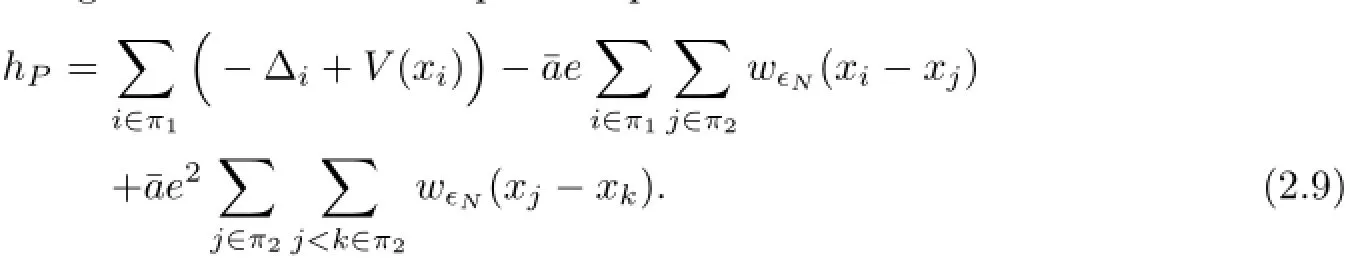
It should be remarked that one may obtain a different form of hP,which however is essentially the same as(2.9).Applying(2.8),we then have the following identity

As the terms hPare all equivalent unitarily,it then suffices to study one of them.Collect the first L variables as Z={z1,···,zL}and the last M variables as Y={y1,···,yM}.In fact,there is no kinetic energy in hPassociated with Y,and the variables y1,···,yMcan be fixed.Thus,if we define hYon q spin-state functions of L variables by
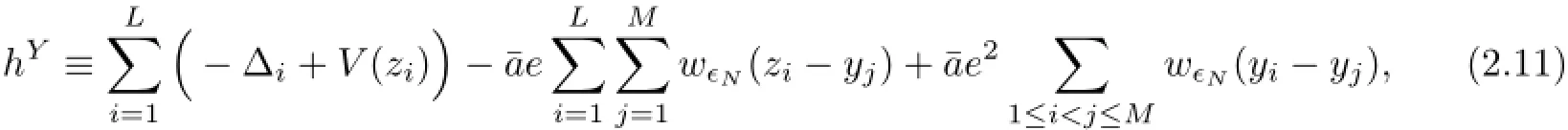
we then have for all P,
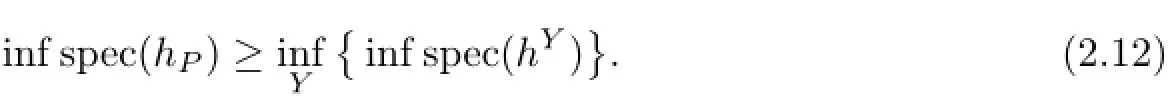

Hence,hYcan be bounded by

As the convolutions become multiplications in Fourier space,we use the positive definiteness of w∈Nto deduce that for any real valued integrable function ρ(z),

where we denote

Expanding the left-hand side of(2.15)and integrating the delta-functions,we obtain
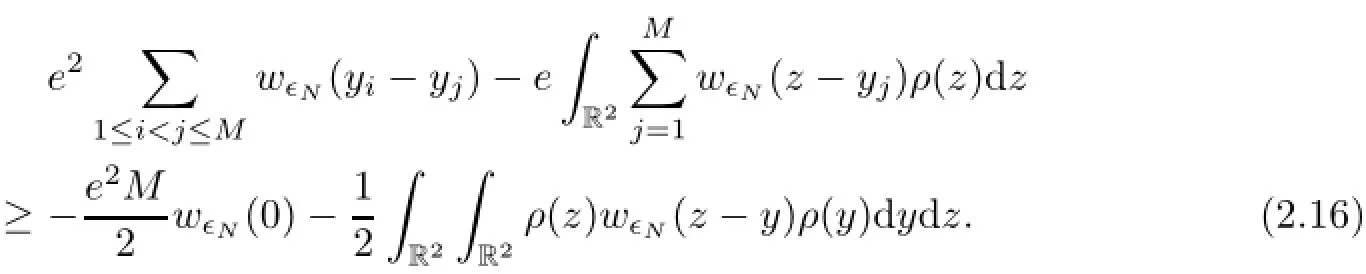
Combining this with(2.14)yields that
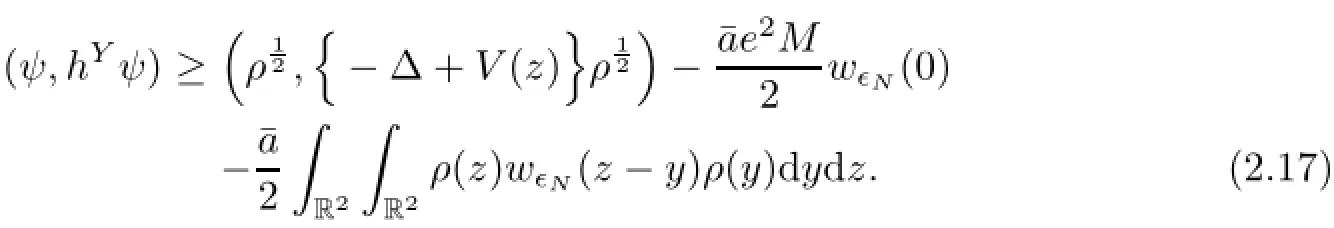
here are four positive parameters L,M(with L+M=N),e,and¯a,which must satisfy(2.10).Setand determine¯a from(2.10),which then imply thatand

where we denote Cw=|w(0)|>0.This estimate and(2.8)then give that
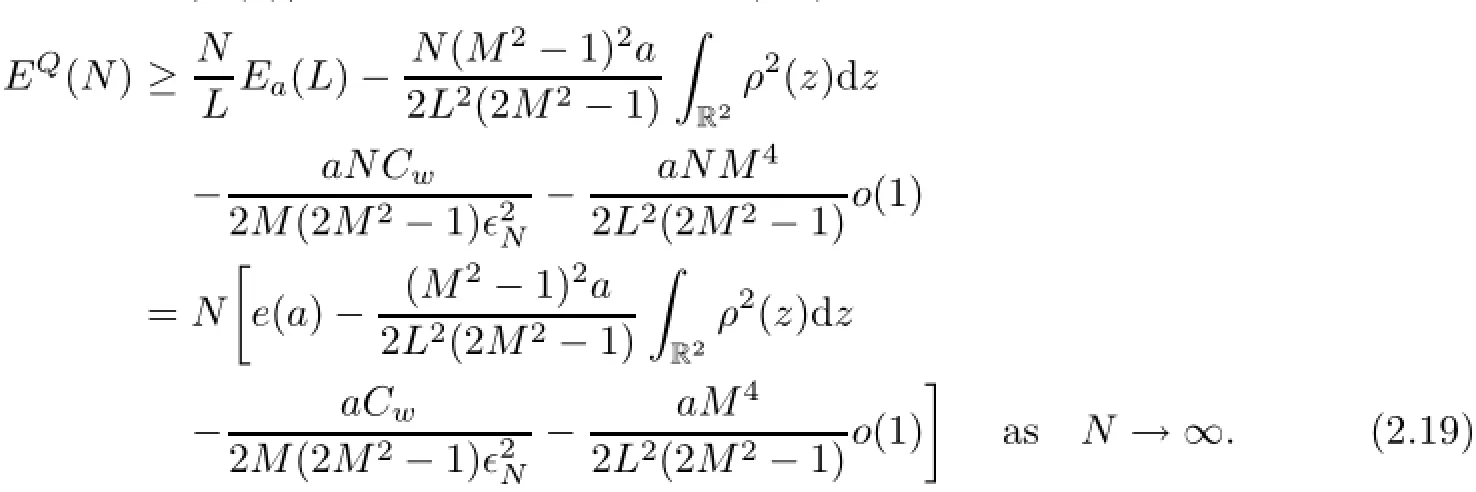

Then,for all a<a∗,

which implies the lower bound of EQ(N)for the case where a<a∗.
Proof of Theorem 1.1The limit(1.16)of Theorem 1.1 now follows immediately from(2.7)and(2.21).Finally,to address the case where a>a∗,choose a nonnegative cut-off functionsuch that ϕ(x)=1 for|x|≤1,and ϕ(x)=0 for|x|≥2.Given a pointset for all τ>0,

where Aτ>0 is chosen so that=1.Takeso that(2.5)holds for all τ>0,and set τ→∞and N→∞.By applying the Gagliardo-Nirenberg inequality(1.10),we then follow(2.5)to derive that(2.6)holds and e(a)=−∞as soon asUsing these facts,we thus conclude thatholds for the case whereThe proof of Theorem 1.1 is therefore completed.
Note added in proofAfter this article was completed,we learned that the mean-field approximation of attractive BEC is also discussed in[M.Lewin,P.T.Nam,and N.Rougerie,The mean-field approximation and the nonlinear Schrüodinger functional for trapped Bose gases,arxiv.org/abs/1405.3220,(2014).].
AcknowledgementsThe authors are grateful to Professor Robert Seiringer very much for his stimulating discussions on this article.The second author would also like to thank his supervisor Professor Yinbin Deng for his enthusiastic guidance and constant encouragement.
References
[1]Anderson M H,Ensher J R,Matthews M R,et al.Observation of Bose-Einstein condensation in a dilute atomic vapor.Science,1995,269:198-201
[2]Baumgartner B,Solovej J P,Yngvason J.Atoms in strong magnetic fields:the high field limit at fixed nuclear charge.Comm Math Phys,2000,212:703-724
[3]Benguria R,Lieb E H.Proof of the stability of highly negative Ions in the absence of the pauli principle. Phys Rev Lett,1983,50:1771-1774
[4]Bloch I,Dalibard J,Zwerger W.Many-body physics with ultracold gases.Rev Mod Phys,2008,80:885-964
[5]Brezis H.Functional Analysis,Sobolev Spaces and Partial Differential Equations.New York:Springer,2001
[6]Cazenave T.Semilinear Schrüodinger Equations.Courant Lecture Notes in Mathematics 10.New York:Courant Institute of Mathematical Science/AMS,2003
[7]Cooper N R.Rapidly rotating atomic gases.Adv Phys,2008,57:539-616
[8]Dalfovo F,Giorgini S,Pitaevskii L P,et al.Theory of Bose-Einstein condensation in trapped gases.Rev Mod Phys,1999,71:463-512
[9]Davis K B,Mewes M O,Andrews M R,et al.Bose-Einstein condensation in a gas of sodium atoms.Phys Rev Lett,1995,75:3969-3973
[10]Erdüos L,Schlein B,Yau H T.Rigorous derivation of the Gross-Pitaevskii equation with a large interaction potential.J Amer Math Soc,2009,22:1099-1156
[11]Fetter A L.Rotating trapped Bose-Einstein condensates.Rev Mod Phys,2009,81:647
[12]Früohlich J,Lenzmann E.Mean-field limit of quantum Bose gases and nonlinear Hartree equation.S´eminaire:´Equations aux D´eriv´ees Partielles,2004:1-26
[13]Gidas B,Ni W M,Nirenberg L.Symmetry of positive solutions of nonlinear elliptic equations in Rn. Mathematical analysis and applications Part A.Adv in Math Suppl Stud,7a.New York-London:Academic Press,1981:369-402
[14]Grech P,Seiringer R.The excitation spectrum for weakly interacting bosons in a trap.Comm Math Phys,2013,322:559-591
[15]Guo Y J,Seiringer R.On the mass concentration for Bose-Einstein condensates with attactive interactions. Lett Math Phys,2014,104:141-156
[16]Guo Y J,Zeng X Y,Zhou H S.Energy estimates and symmetry breaking in attractive Bose-Einstein condensates with ring-shaped potentials[J/OL].Ann I H Poincar´e-AN,2015,http://dx.doi.org/10.1016/j.anihpc. 2015.01.005
[17]Huepe C,Metens S,Dewel G,et al.Decay rates in attractive Bose-Einstein condensates.Phys Rev Lett,1999,82:1616-1619
[18]Kagan Y,Muryshev A E,Shlyapnikov G V.Collapse and Bose-Einstein condensation in a trapped Bose gas with nagative scattering length.Phys Rev Lett,1998,81:933-937
[19]Kwong M K.Uniqueness of positive solutions of∆u−u+up=0 in RN.Arch Rational Mech Anal,1989,105:243-266
[20]Li Y,Ni W M.Radial symmetry of positive solutions of nonlinear elliptic equations in Rn.Comm Partial Differential Equations,1993,18:1043-1054
[21]Lieb E H,Seiringer R.Proof of Bose-Einstein condensation for dilute trapped gases.Phys Rev Lett,2002,88:170409-1-4
[22]Lieb E H,Seiringer R.Derivation of the Gross-Pitaevskii equation for rotating Bose gases.Comm Math Phys,2006,264:505-537
[23]Lieb E H,Seiringer R,Solovej J P,et al.The mathematics of the Bose gas and its condensation.Oberwolfach Seminars 34.Basel:Birkhüauser Verlag,2005
[24]Lieb E H,Seiringer R,Yngvason J.Bosons in a trap:A rigorous derivation of the Gross-Pitaevskii energy functional.Phys Rev A,2000,61:043602-1-13
[25]Lieb E H,Seiringer R,Yngvason J.A rigorous derivation of the Gross-Pitaevskii energy functional for a two-dimensional Bose gas.Comm Math Phys,2001,224:17-31
[26]Lieb E H,Yau H T.The Chandrasekhar theory of stellar collapse as the limit of quantum mechanics.Comm Math Phys,1987,112:147-174
[27]Seiringer R.The excitation spectrum for weakly interacting bosons.Comm Math Phys,2011,306:565-578
[28]Seiringer R,Yngvason J,Zagrebnov V A.Disordered Bose-Einstein condensates with interaction in one dimension.J Stat Mech,2012,2012:P11007
[29]Weinstein M I.Nonlinear Schrüodinger equations and sharp interpolations estimates.Comm Math Phys,1983,87:567-576
[30]Zhang J.Stability of attractive Bose-Einstein condensates.J Statist Phys,2000,101:731-746
August 6,2014;revised October 12,2015.This work is partially supported by the Scientific Research Foundation for the Returned Overseas Chinese Scholars,State Education Ministry of China,and National Center for Mathematics and Interdisciplinary Sciences in China.
†Corresponding author.
 Acta Mathematica Scientia(English Series)2016年2期
Acta Mathematica Scientia(English Series)2016年2期
- Acta Mathematica Scientia(English Series)的其它文章
- FREDHOLM OPERATORS ON THE SPACE OF BOUNDED SEQUENCES∗
- GENERAL SPLIT FEASIBILITY PROBLEMS FOR TWO FAMILIES OF NONEXPANSIVE MAPPINGS IN HILBERT SPACES∗
- ON APPROXIMATELY(p,q)-WRIGHT AFFINE FUNCTIONS AND INNER PRODUCT SPACES∗
- TOPOLOGICAL ENTROPY OF PERIODIC COVEN CELLULAR AUTOMATA∗
- DISCRETE GALERKIN METHOD FOR FRACTIONAL INTEGRO-DIFFERENTIAL EQUATIONS∗
- MULTIPLICITY OF SOLUTIONS FOR A QUASILINEAR ELLIPTIC EQUATION∗
