GENERAL SPLIT FEASIBILITY PROBLEMS FOR TWO FAMILIES OF NONEXPANSIVE MAPPINGS IN HILBERT SPACES∗

Jinfang TANG（唐金芳）

Department of Mathematics，Yibin University，Yibin 644007，China

E-mail∶jinfangt 79@163.com

Shih-sen CHANG（张石生）

Center for General Education，China Medical University，Taichung 40402，Taiwan

E-mail∶changss2013@163.com

Min LIU（刘敏）

Department of Mathematics，Yibin University，Yibin 644007，China

E-mail∶liuminybsc@163.com



GENERAL SPLIT FEASIBILITY PROBLEMS FOR TWO FAMILIES OF NONEXPANSIVE MAPPINGS IN HILBERT SPACES∗

Jinfang TANG（唐金芳）

Department of Mathematics，Yibin University，Yibin 644007，China

E-mail∶jinfangt 79@163.com

Shih-sen CHANG（张石生）

Center for General Education，China Medical University，Taichung 40402，Taiwan

E-mail∶changss2013@163.com

Min LIU（刘敏）

Department of Mathematics，Yibin University，Yibin 644007，China

E-mail∶liuminybsc@163.com

The purpose of this article is to introduce a general split feasibility problems for two families of nonexpansive mappings in Hilbert spaces.We prove that the sequence generated by the proposed new algorithm converges strongly to a solution of the general split feasibility problem.Our results extend and improve some recent known results.

General split feasibility problems；nonexpansive mappings；Hilbert space；strong convergence

2010 MR Subject Classification90C25；47H09；47J25

1　Introduction

Let H and K be infinite-dimensional real Hilbert spaces，and let A：H→K be a bounded linear operator.Letandbe the families of nonempty closed convex subsets of H and K，respectively.Let F（T）be the fixed point of the mapping T.

（a）The convex feasibility problem（CFP）is formulated as the problem of finding a point x∗with the property：

（b）The split feasibility problem（SFP）is formulated as the problem of finding a point x∗with the property：

where C and Q are nonempty，closed and convex subsets of H and K，respectively.

（c）The multiple-set split feasibility problem（MSSFP）is formulated as the problem of finding a point x∗with the property：

（d）The general split feasibility problem（GSFP）is formulated as the problem of finding a point x∗with the property：

There is a considerable investigation on CFP in view of its applications in various disciplines such as image restoration，computer tomograph，and radiation therapy treatment planning［1］. The split feasibility problem SFP in the setting of finite-dimensional Hilbert spaces was first introduced by Censor and Elfving［2］for modelling inverse problems which arise from phase retrievals and in medical image reconstruction［3］.Since then，a lot of work has been done on finding a solution of SFP and MSSFP；see，for example，［2-17］.

In 2010，Xu［13］considered the SFP in the setting of infinite-dimensional Hilbert spaces and studied some algorithms and its convergence.In particular，he applied Mann's algorithm to the SFP and proposed an algorithm which is proved to be weakly convergent to a solution of the SFP.He also established the strong convergence result，which shows that the minimum-norm solution can be obtained.

In 2011，Wang and Xu［14］proposed the following cyclic algorithm to solve MSSFP：

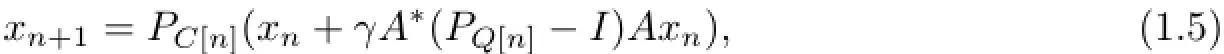
where［n］：=n（modp）（mod function take values in｛1，2，···，p｝，andThey shown that the sequence｛xn｝converged weakly to a solution of MSSFP provided the solution exists.

To study strong convergence to a solution of MSSFP，in 2013，Eslamian and Latif［15］proposed the following algorithm to solve GSFP：

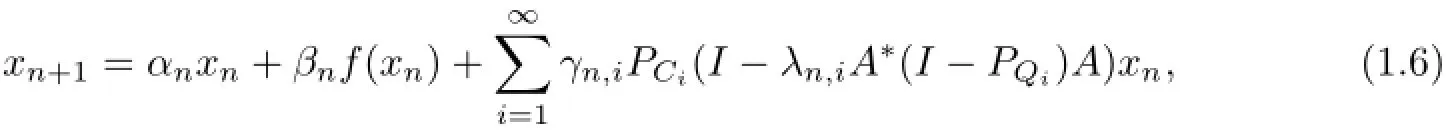
In 2013，He and Zhao［16］introduced the following relaxed CQ algorithm such that the strong convergence was guaranteed in infinite-dimensional Hilbert spaces：

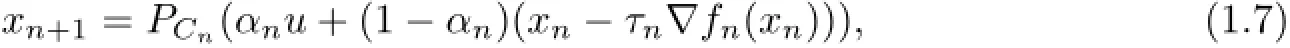
To further study strong convergence to a solution of GSFP，first we introduce a general form of the general split feasibility problem for two families of firmly nonexpansive mappings as follows：

（e）General split feasibility problem for two families of firmly nonexpansive mappings is to find a point x∗such that

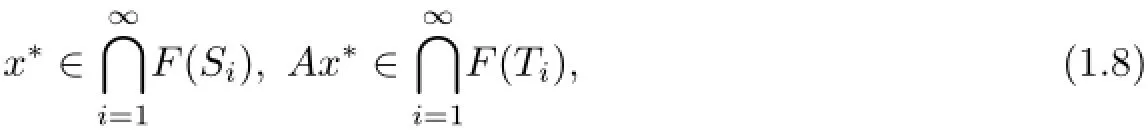
where｛Si｝，｛Ti｝are two families of firmly nonexpansive mappings.We denote by Ω the solution set of the problem（1.8）.

Motivated and inspired by the researches going on in the sections of split feasibility problems，the purpose of this article is to introduce a new viscosity iterative algorithm for general split feasibility problems（1.8）in infinite dimensional Hilbert spaces.Under suitable conditions we prove the sequence converges strongly to a point in the set of solutions of general split feasibility problems for two families of firmly nonexpansive mappings.Our result extends and improves the corresponding results of some others.

2　Preliminaries and Lemmas

Throughout the rest of this article，we assume that H，H1，and H2are real Hilbert spaces，A is a bounded linear operator from H1to H2，and I is the identity operator on H，H1，or H2. If f：H→R is a differentiable function，then we denote by∇f the gradient of the function f.We will also use the notations：→to denote the strong convergence，⇀to denote the weak convergence and

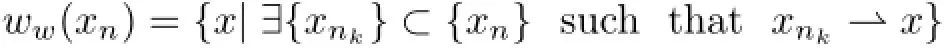
to denote the weak limit set of｛xn｝.

Let C be a closed and convex subset of H.For every point x∈H，there exists a unique nearest point in C，denoted by PCx satisfing

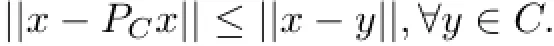
The operator PCis called the metric projection of H onto C.The metric projection PCis characterized by the following inequality：

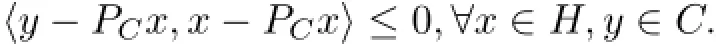
Recall that a mapping T：H→H is said to be nonexpansive if

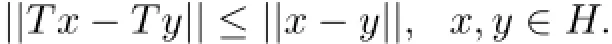
A mapping T：H→H is said to be firmly nonexpansive if

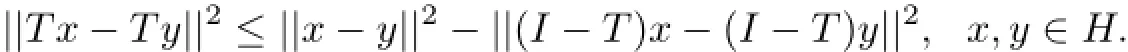
A mapping T：H→H is said to be demi-closed at origin if for any sequencewith xn⇀x∗and

It is easy to prove that if T：H→H is a firmly nonexpansive mapping，then T is demiclosed at origin.

A function f：H→R is called convex if

Lemma 2.1［17］Let T：H2→H2be a firmly nonexpansive mapping such that||（I−T）x|| is a convex function from H2to¯R=［−∞，+∞］.Let A：H1→H2be a bounded linear operator and

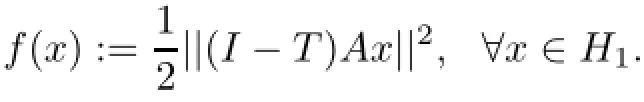
Then

（i）∇f（x）=A∗（I−T）Ax，x∈H1.

（ii）∇f is||A||2-Lipschitz，that is，||∇f（x）−∇f（y）||≤||A||2||x−y||，x，y∈H1.

Lemma 2.2［17］Let T：H→H be an operator.The following statements are equivalent：

（i）T is firmly nonexpansive.

（ii）||Tx−Ty||2≤〈x−y，Tx−Ty〉，∀x，y∈H.

（iii）I−T is firmly nonexpansive.

The following results play an important role in this article.

Lemma 2.4［18］Let X be a real Hilbert space，then we have

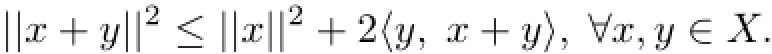
Lemma 2.5［19］Let H be a Hilbert space and let｛xn｝be a sequence in H.Then for any given sequenceand for any positive integer i，j with i＜j，

Lemma 2.6［20］Let｛an｝be a sequence of nonnegative real numbers such that

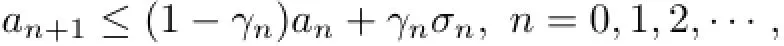
where｛γn｝is a sequence in（0，1），and｛σn｝is a sequence in R such that

Lemma 2.7［21］Let｛tn｝be a sequence of real numbers such that there exists a subsequence｛ni｝of｛n｝such that tni＜tni+1for all i∈N.Then，there exists a nondecreasing sequence｛τ（n）｝⊂N such that τ（n）→∞，and the following properties are satisfied by all（sufficiently large）numbers n∈N：

In fact，

3　Main Result

In the following，we propose an algorithm and prove that the sequence generated by the proposed method converges strongly to a solution of the GSFP（1.8）.

Theorem 3.1Let H1，H2be two real Hilbert spaces.Let A：H1→H2be a bounded linear operatorbe a family of firmly nonexpansive mappings，and｛Ti：be another family of firmly nonexpansive mappings such that for any i∈N，is a convex function from H2toAssume that GSFP（1.8）has a nonempty solution set Ω.Suppose that h：H1→H1is a α-contraction mapping and let｛xn｝be a sequence generated by x0∈H1as follows

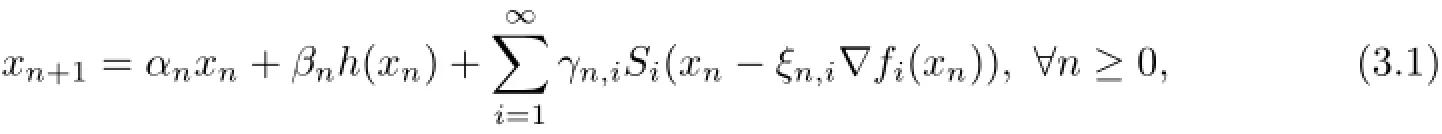
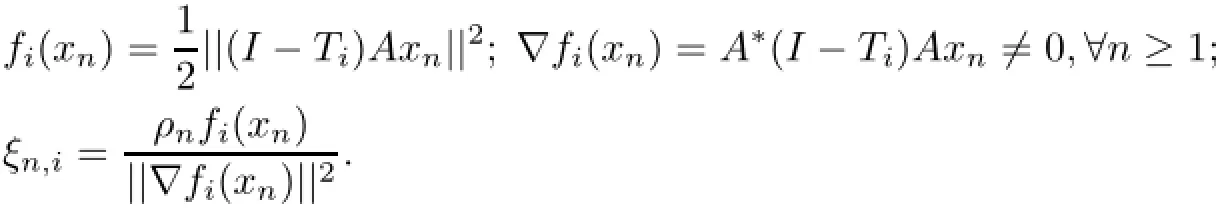
If the sequences｛ρn｝⊂（0，4），｛αn｝，｛βn｝，｛γn，i｝⊂（0，1）satisfy the following conditions：

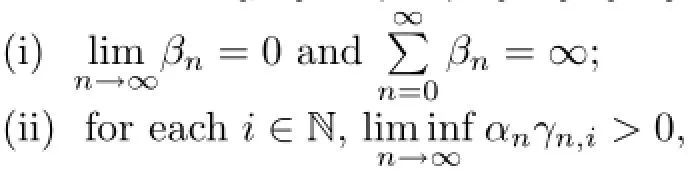
then the sequence｛xn｝converges strongly to x∗∈Ω，where x∗=

ProofFirst，we show that｛xn｝is bounded.In fact，for any p∈Ω，we haveObserving that each I−Tiis firmly nonexpansive， from Lemma 2.2（ii）we have

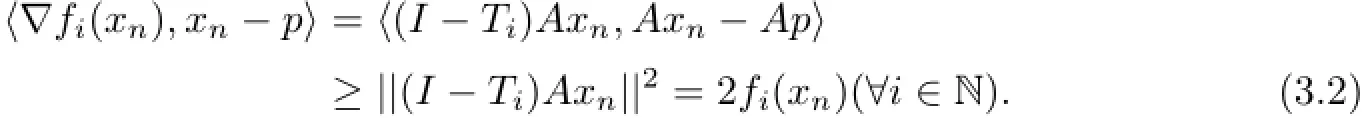
Hence，for any i∈N we have

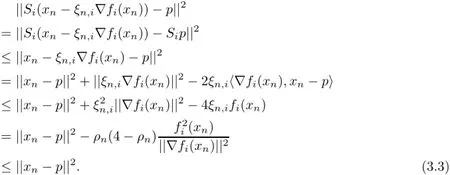
This implies that for any i∈N，

From（3.1）and（3.4），we have

By induction，we have

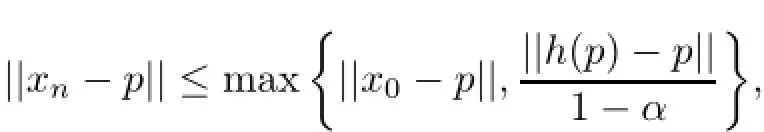
which implies that｛xn｝is bounded，and so is｛h（xn）｝.

Using Lemma 2.5 and（3.3），for any p∈Ω and i∈N，we have

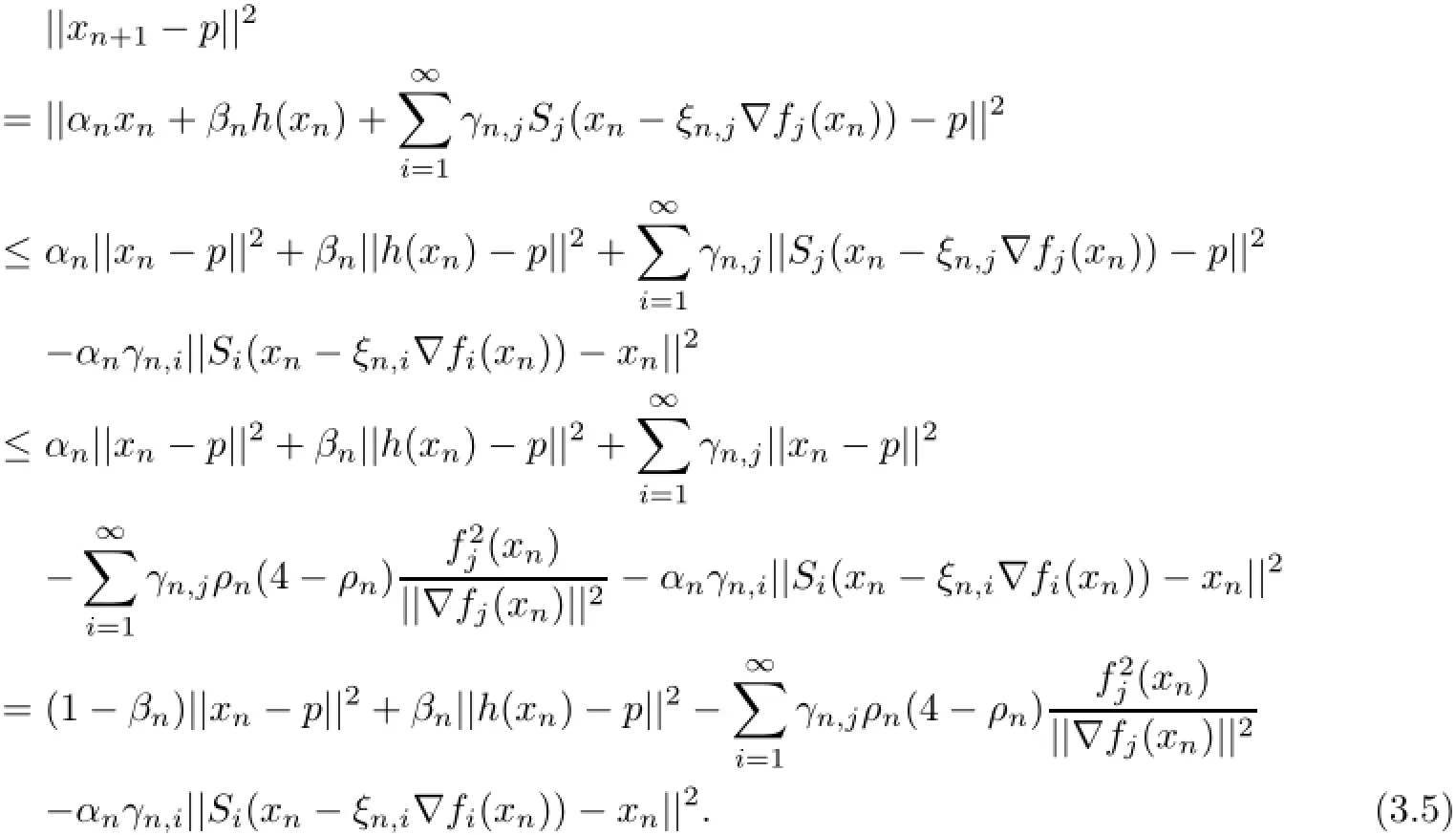
On the other hand，without loss of generality，we may assume that there exists a constant σ＞0 such that

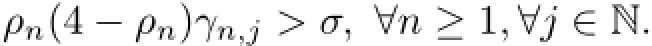
Hence，for each i∈N，we have

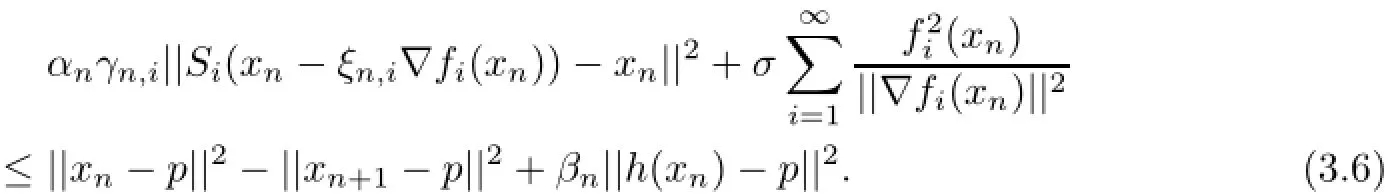
As PΩh is a contraction of H1into itself，there exists a unique element x∗∈Ω such that x∗=PΩh（x∗）.

Now，we prove xn→x∗as n→∞by employing the technique studied by Maing´e［21］. For the purpose，we consider two cases.

Case 1Assume that｛||xn−p||｝is a monotone sequence.In other words，for n0large enough，｛||xn−p||｝n≥n0is either nondecreasing or nonincreasing.As｛||xn−p||｝is bounded， so｛||xn−p||｝is convergent.Asis bounded，from（3.6）we get

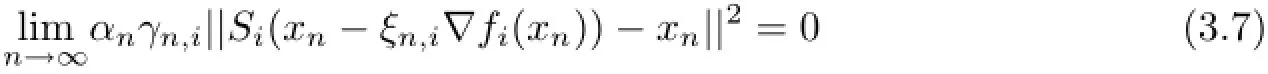
and

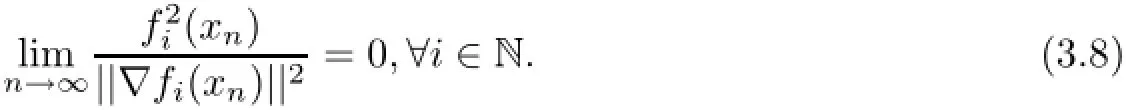
By condition（ii）we obtain

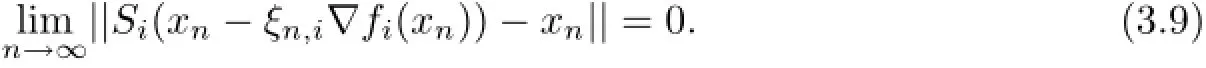
Now，we prove that

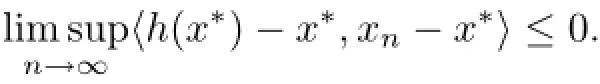
It follows from Lemma 2.1（ii）that for all n≥1 and i∈N，

This implies that for each i∈N，｛||∇fi（xn）||｝is bounded.From（3.8）it yields that for each i∈N，fi（xn）→0，namely for each i∈N，

By the way，we have

As｛xn｝is bounded，there exists a subsequence｛xnk｝of｛xn｝which converges weakly to w∈H1，that is，w∈ww（xn）.From the definition of A，we have

In fact，from（3.10）we have

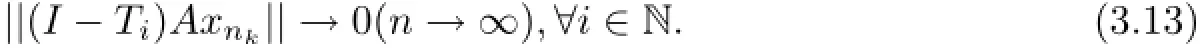
As each Tiis demi-closed at origin，from（3.12）and（3.13）we have Aw∈F（Ti），that is，

Thus，we have

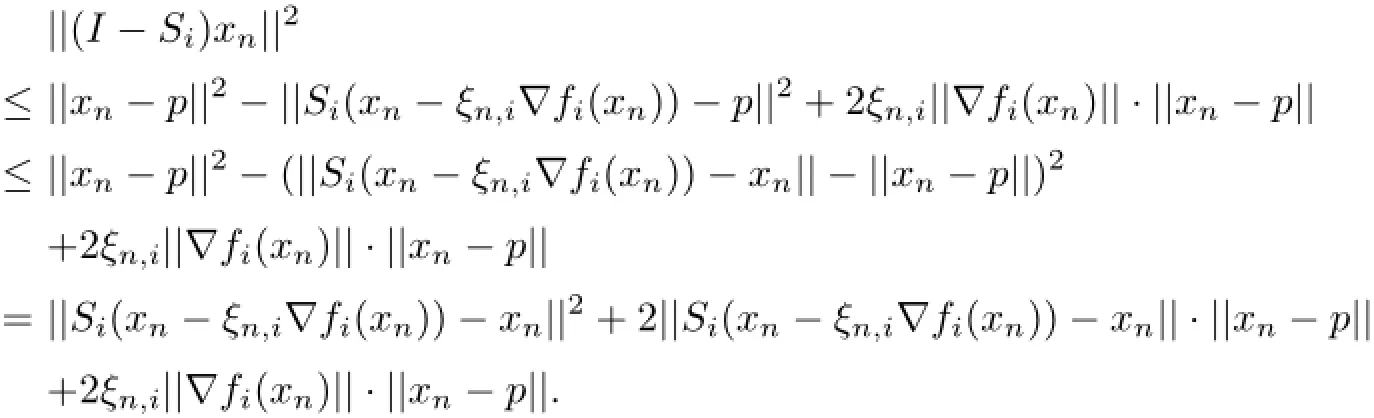
It follows from（3.9）and（3.11）that

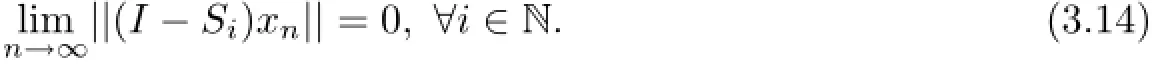
In view of xnk⇀w and each Si（i∈N）being demi-closed at origin，we get wHence w∈Ω and then ww（xn）⊂Ω.

Therefore，in view of x∗=PΩh（x∗），from the characteristic of metric projection PΩ，we have

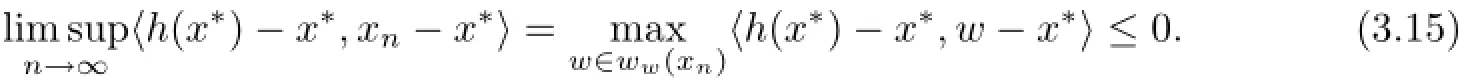
Finally，we prove that xn→x∗=PΩh（x∗）.Applying Lemma 2.4 and（3.4），we have

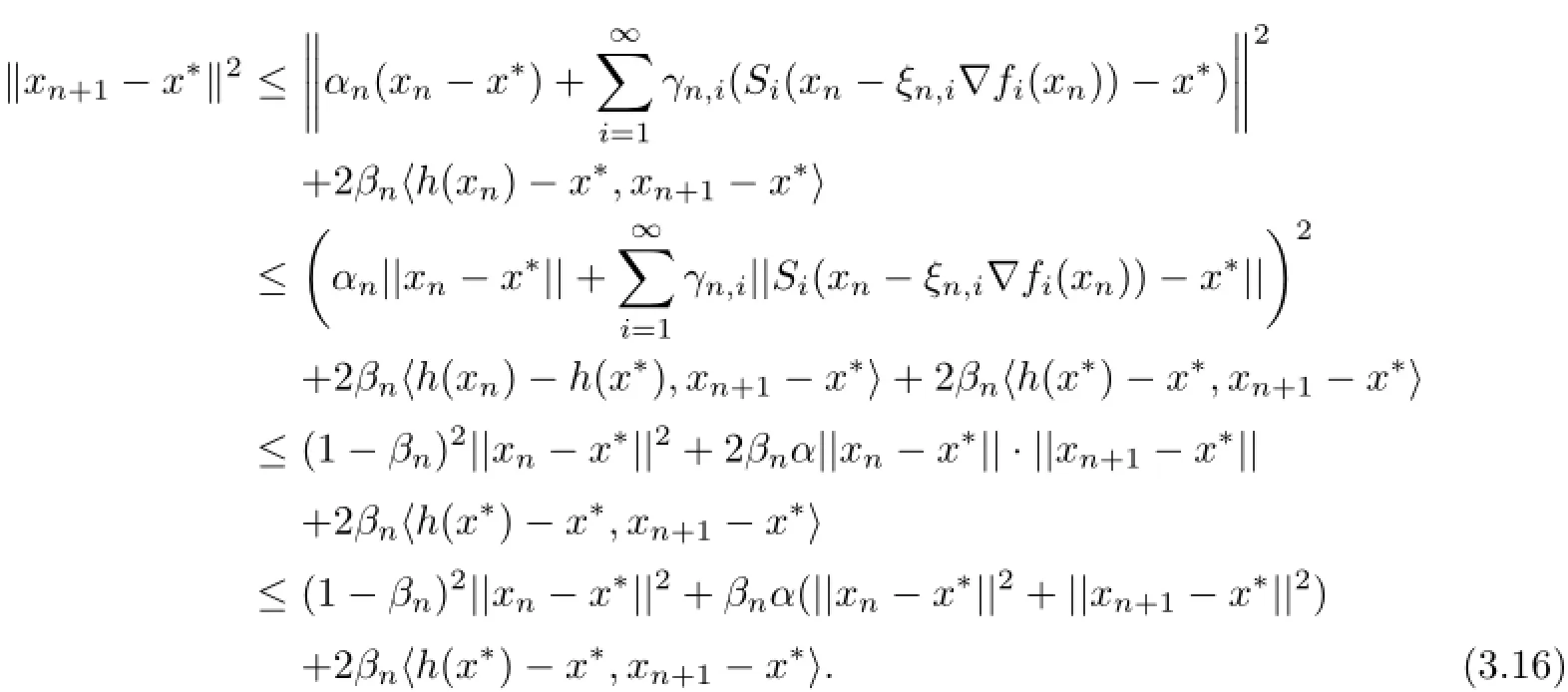
This implies that

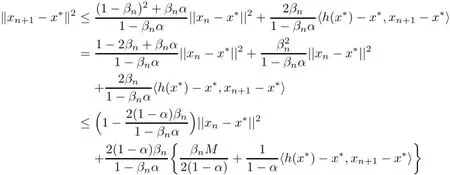
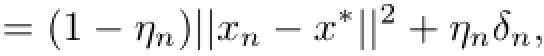
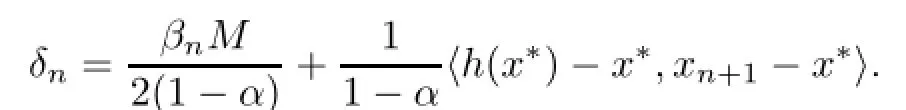
Case 2Assume that｛||xn−p||｝is not a monotone sequence.Then，we can define an integer sequence｛τ（n）｝for all n≥n0（for some n0large enough）by

Clearly，τ（n）is a nondecreasing sequence such that τ（n）→∞as n→∞and for all n≥n0，

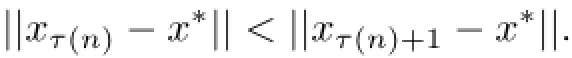
From（3.6）we obtain

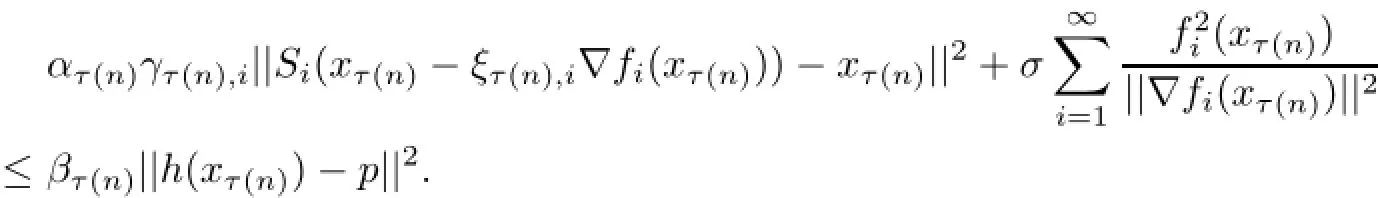
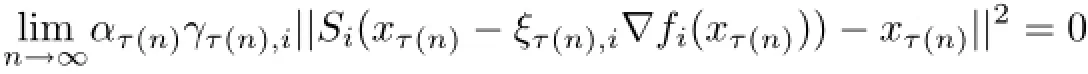
and

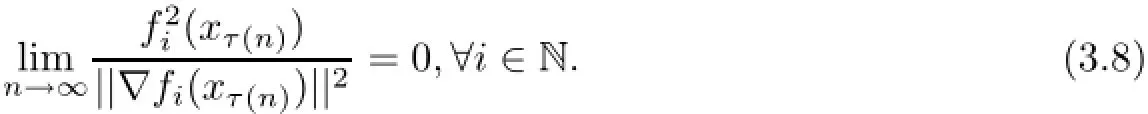
Following an argument similar to that in Case 1，we have ww（xτ（n））⊂Ω.Therefore，from the characteristic of metric projection PΩ，we have

And by similar argument，we have

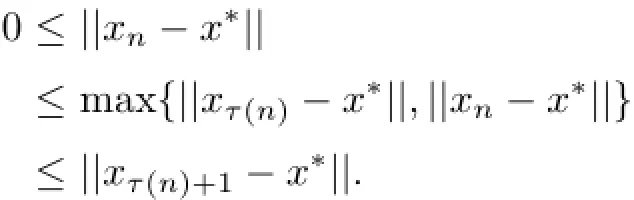
Therefore，the sequence｛xn｝converges strongly to x∗=PΩh（x∗）.

This completes the proof.

RemarkIt should be pointed out that the condition“||（I−Ti）x||is a convex function from H2to¯R”in Theorem 3.1 can be replaced by the condition“the function fi（x）=is G´ateaux differentiable and∇fi（x）=A∗（I−Ti）Ax”.

4　An Application and a Numerical Example for Split Equilibrium Problems in Hilbert Spaces

In this section，we shall utilize Theorem 3.1 to give a numerical example for split equilibrium problems in Hilbert spaces.

Let D be a nonempty closed and convex subset of a real Hilbert space H.A bifunction g：D×D→（−∞，+∞）is said to be a equilibrium function，if it satisfies the following conditions：

（A1）g（x，x）=0，for all x∈D；

（A2）g is monotone，that is，g（x，y）+g（y，x）≤0 for all x，y∈D；

The“so-called”equilibrium problem with respect to the equilibrium function g is

Its solution set is denoted by EP（g）.

For given λ＞0 and x∈H，the resolvent of the equilibrium function g is the operator Rλ，g：H→D defined by

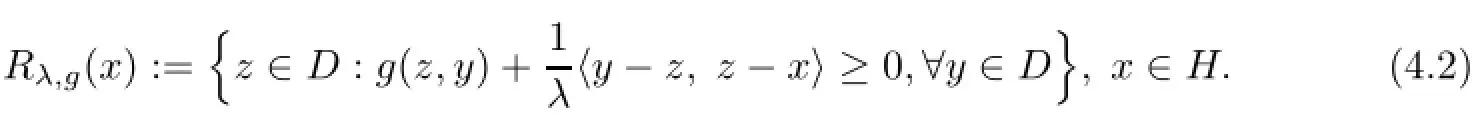
Proposition 4.1［22］The resolvent operator Rλ，gof the equilibrium function g has the following properties：

（1）Rλ，gis single-valued；

（2）F（Rλ，g）=EP（g）is a nonempty closed and convex subset of D；

（3）Rλ，gis a firmly nonexpansive mapping.

Let H1and H2be two real Hilbert spaces.Let C be a nonempty closed convex subset of H1，Q be a nonempty closed convex subset of H2.Let h：C×C→R and g：Q×Q→R be two equilibrium functions.Let A：H1→H2be a bounded linear operator with adjoint operator A∗.For given λ＞0，let Rλ，hand Rλ，gbe the resolvent of h and g（defined by（4.2）），respectively.

The“so-called”split equilibrium problem with respect to the equilibrium function h，g is to find x∗∈C such that

Let H1=H2=R2with standard norm and inner product.For each α=（α1，α2）and z=（z1，z2）∈R2，define operators A as

It is easy to prove that

Then，A is a bounded linear operator from R2into R2and A∗：R2→R2is the adjoint operator of A.The norm of A

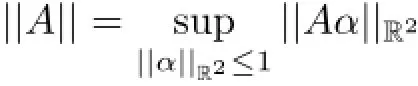
Put

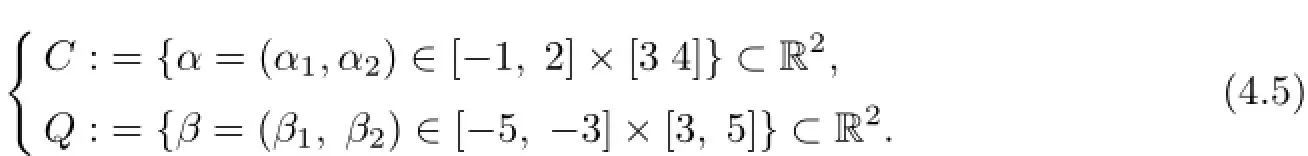
For each α=（α1，α2）∈C and β=（β1，β2）∈Q，define functions：

Let

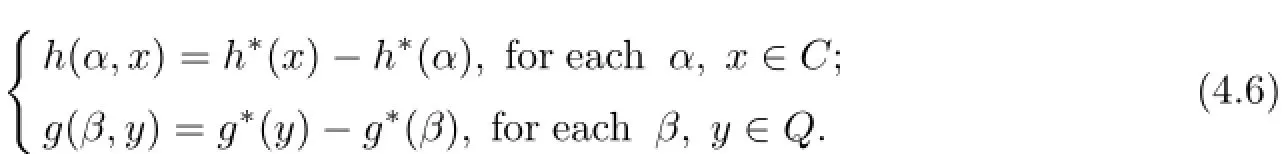
It is easy to know that h：C×C→R and g：Q×Q→R both are the equilibrium functions satisfying conditions（A1）-（A4）.Let EP（h）（resp.EP（g））be the set of solutions of equilibrium problem with respect to h（resp.g）.It is not hard to verify that

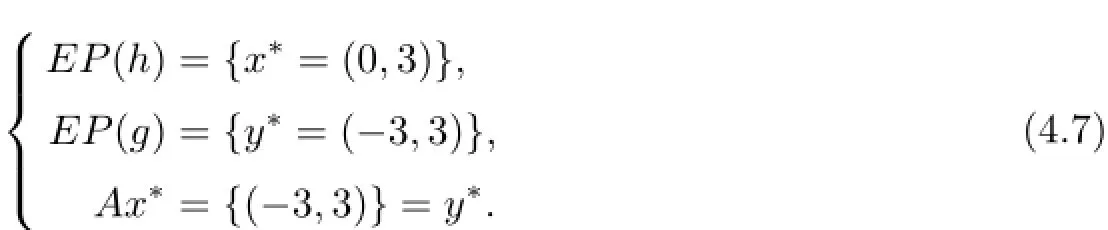
This implies that（x∗，y∗）=（（0，3），（−3，3））∈C×Q is the unique solution of the following split equilibrium problem with respect to h，g

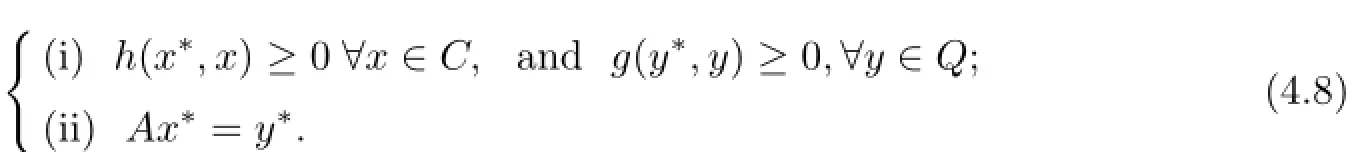
Denote by Ω the set of solutions of the split equilibrium problem（4.8），then we have

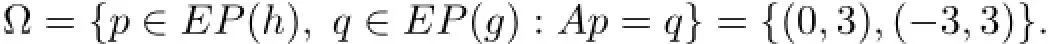
For given λ＞0，let Rλ，hand Rλ，gbe the resolvent of h and g（defined by（4.2）），respectively. Let S=Rλ，hand T=Rλ，g.By Proposition 4.1，T and S both are firmly nonexpansive mappings and F（S）=EP（h），F（T）=EP（g）.Hence from Theorem 3.1，we can obtain the following

Theorem 4.2Let H1=H2=R2，T，S，A，A∗and C，Q be the same as above.Let the function|（I−T）Ax||2be G´ateaux differentiable and∇f（x）=A∗（I−T）Ax.Suppose further that h：R2→R2is a α-contraction mapping and｛xn｝is a sequence generated by x0∈R2

where｛αn｝，｛βn｝，｛γn｝⊂（0，1）with αn+βn+γn=1，∀n≥1，A∗（I−T）Axn6=0，∀n≥1 and

If the sequences satisfy the following conditions：

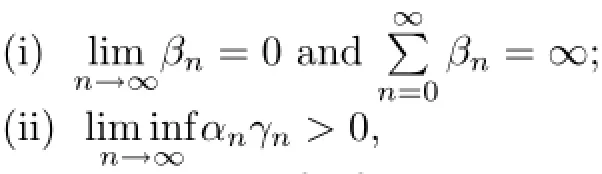
then the sequence｛xn｝converges strongly to x∗=（0，3）with Ax∗=（−3，3）and Ω=｛（x∗，Ax∗）｝（the solution set of the split equilibrium problem（4.8））.

References

［1］Combettes P L.The convex feasibility problem in image recovery.Advances in Imaging and Electron Physics，1996，95：155-270

［2］Censor Y，Elfving T.A multiprojection algorithm using Bregman projections in a product space.Numerical Algorithms，1994，8：221-239

［3］Byrne C.Iterative oblique projection onto convex sets and the split feasibility problem.Inverse Problems，2002，18（2）：441-453

［4］Aleyner A，Reich S.Block-iterative algorithms for solving convex feasibility problems in Hilbert and in Banach spaces.Journal of Mathematical Analysis and Applications，2008，343（1）：427-435

［5］Bauschke H H，Borwein J M.On projection algorithms for solving convex feasibility problems.SIAM Review，1996，8（3）：367-426

［6］Moudafi A.A relaxed alternating CQ-algorithm for convex feasibility problems.Nonlinear Analysis，2013，79：117-121

［7］Masad E，Reich S.A note on the multiple-set split convex feasibility problem in Hilbert space.Journal of Nonlinear and Convex Analysis，2007，8：367-371

［8］Yao Y，Chen R，Marino G，et al.Applications of fixed point and optimization methods to the multiple-sets split feasibility problem.Journal of Applied Mathematics，2012，2012：Article ID 927530

［9］Yang Q.The relaxed CQ algorithm for solving the split feasibility problem.Inverse Problems，2004，20：1261-1266

［10］Zhao J，Yang Q.Several solution methods for the split feasibility problem.Inverse Problems，2005，21：1791-1799

［11］Quan J，Chang S.S，Zhang X.Multiple-set split feasibility problems for κ-strictly pseudononspreading mappings in Hilbert spaces.Abstract and applied analysis，2013.article ID 342545

［12］Xu H K.A variable Krasnosel’skii-Mann algorithm and the multiple-set split feasibility problem.Inverse Problems，2006，22：2021-2034

［13］Xu H K.Iterative methods for the split feasibility problem in infinite-dimensional Hilbert spaces.Inverse Problems，2010，26：Article ID 105018

［14］Wang F，Xu H K.Cyclic algorithms for split feasibility problems in Hilbert spaces.Nonlinear Analysis：Theory，Methods and Applications，2011，74（12）：4105-4111

［15］Eslamian M，Latif A.General split feasibility problems in Hilbert spaces.Abstract and Applied Analysis Volume 2013.Article ID 805104

［16］He S，Zhao Z.Strong Convergence of A Relaxed CQ Algorithm for the Split Feasibility Problem.Journal of Inequalities and Applications，2013.doi：10.1186/1029-242X-2013-197

［17］Tang J F，Chang S S，Yuan F.A strong convergence theorem for equilibrium problems and split feasibility problems in Hilbert spaces.Fixed point theory and applications，2014，2014：36

［18］Chang S S.On Chidume’s open questions and approximate solutions for multi-valued strongly accretive mapping equations in Banach spaces.J.Math.Anal.Applications，1997，216：94-111

［19］Chang S S，Kim J K，Wang X R，Modified block iterative algorithm for solving convex feasibility problems in Banach spaces.Journal of Inequalities and Applications，2010.Article ID869684

［20］Xu H K.Iterative algorithms for nonlinnear operators.J Lond Math Soc，2002，66：240-256

［21］Maing´e P E.Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization.Set-Valued Analysis，2008，16：899-912

［22］Blum E，Oettli W.From optimization and variational inequalities to equilibrium problems.Math Stud，1994，63：123-145

December 15，2014；revised July 11，2015.Supported by the Scientific Research Fund of Sichuan Provincial Department of Science and Technology（2015JY0165，2011JYZ011），the Scientific Research Fund of Sichuan Provincial Education Department（14ZA0271），the Scientific Research Project of Yibin University（2013YY06），the Natural Science Foundation of China Medical University，Taiwan，and the National Natural Science Foundation of China（11361070）.

†Corresponding author