顶吹转炉吹炼过程反应速率数模研究
陈志刚,邹贤,张源,涂百乐,周斌
(安徽铜陵有色稀贵金属分公司,安徽铜陵,244021)
顶吹转炉吹炼过程反应速率数模研究
陈志刚,邹贤,张源,涂百乐,周斌
(安徽铜陵有色稀贵金属分公司,安徽铜陵,244021)
本文依据界面更新理论,研究了顶吹转炉吹炼过程数学模型,分析了吹炼阶段限制性环节,提出了顶吹转炉吹炼速率公式,并以生产数据加以验证,最终获得顶吹转炉吹炼实践操作较优工艺参数。实践证明:参数选择与运用具有比较优势。
顶吹转炉;吹炼;反应速率;数模研究
引言
顶吹转炉又称为氧气斜吹转炉,由于炉体倾斜,反应面积增加,同时炉体不断地旋转,不断更新反应界面,显著提高了反应速度[1]。所以顶吹转炉常用来处理那些成分复杂、处理难度大的复杂物料。
顶吹转炉冶炼为周期性作业,一台炉子内完成熔炼、吹炼(精炼)作业过程。有价金属主要在熔炼阶段被还原富集,贱金属及杂质元素主要在吹炼阶段以氧化造渣方式和烟尘形式除去[2]。
本文依据界面更新理论[3],研究建立顶吹转炉吹炼阶段数学模型,进而研究顶吹转炉吹炼过程速率公式并以生产数据加以验证,并获得顶吹转炉吹炼实践操作较优工艺参数。
1 顶吹转炉吹炼阶段限制性环节分析
在吹炼阶段中,吹炼喷枪往炉内吹入高压压缩空气,压缩空气吹开熔体表面渣层,与熔体直接接触发生氧化反应,氧化物造渣——吹炼渣。
这些氧化反应是典型的气液反应[4],反应主要步骤有:①压缩空气中的氧气向熔体表面传质;②氧气与熔体中物质发生反应;③固体产物造渣,气体产物逸出。
在吹炼阶段,炉内温度高达1200℃,各类反应极为迅速,吹炼渣浮于熔体表面,和残存的熔炼渣聚集在一起,严重阻碍压缩空气向熔体中的进一步传质。因此,②③为非限制性环节,①是吹炼过程限制性环节,针对限制性环节建立数学模型。
2 限制性环节数学模型
2.1喷嘴与液面临界距离公式
在吹炼作业中,当喷嘴压缩空气压力达到临界压力时,压缩空气会吹开喷嘴周围渣层,新反应界面与氧气持续反应。液面和液面最上面渣粒A建立数学模型(见图1)。

图1 液面和液面最上面渣粒数学模型
所以,喷嘴周围反应界面更新速率是影响顶吹转炉吹炼速率的关键因素。假设喷嘴出口压力为P0,喷嘴面积为S0,喷嘴与液面的临界距离L0,喷射角的一半为β,压缩空气到达液面时压力为P液,喷射面积为S液。那么:P0·S0=P液·S液(1)又S液=π(L0tanβ)2(2)那么:

当渣粒A受到的喷嘴空气压力F斜面方向分压力F1和重力G斜面反方向分力F2平衡时,此时渣粒被吹开,露出新反应界面,有
F1= P·SA·sinβ (4)
F2=GA·sinα (5)
当F1=F2,整理并对微粒半径rA积分,积分区间[0,L0tanβ],得喷嘴与液面的临界距离L0为

K——设计系数;
P0——喷嘴出口压力;
ρA——渣的比重;
g——重力加速度;
α——液面倾斜角;
β——喷嘴喷射角的一半。
喷嘴与液面的实际距离为L,当L>L0时,喷嘴压缩空气到达液面时的压力不足以吹开液面的渣层,吹炼反应缓慢;当L<L0时,吹炼反应能够快速发生,但L进一步减少时,吹开面积减小,吹炼速率反而减小。只有当L=L0时,吹炼反应最快。
2.2顶吹转炉吹炼反应速率公式
未通入压缩空气前,当微粒球团随炉转动到X位置时,球团所在料面的倾角为α,微粒球团受到竖直向下的重力G和炉体转动所产生的离心力F向,对微粒球团建立数学模型(见图2)。
当微粒球团炉壁切线方向的重力分力和摩擦力相等,微粒球团处于临界状态,此时:

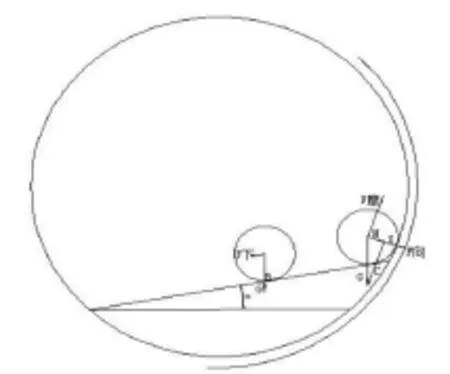
图2 未通入压缩空气前微粒球团数模
则熔体线速度为:其中:
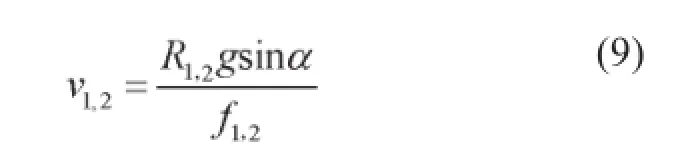
R1,2——最外围、最内层熔体到炉中心的距离;
f1,2——最外围熔体与炉壁、熔体层间的摩擦系数。
熔体各点角

炉内参与反应的熔体厚度
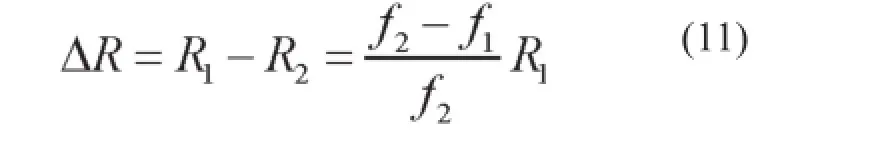
熔体顶端至底端的距离为L长,炉内熔体总面积

炉体转速为n(rad/min),角速度ω,Δt时间熔体转动角度为∠A=ωΔt。
Δt时间内,参与反应的物料体积ΔV和物料量Δm分别为

ƒ1与ƒ2均与熔体黏度η有关[5],令ƒ1=c·η,ƒ2=d·η,,c、d均为常数,反应速率
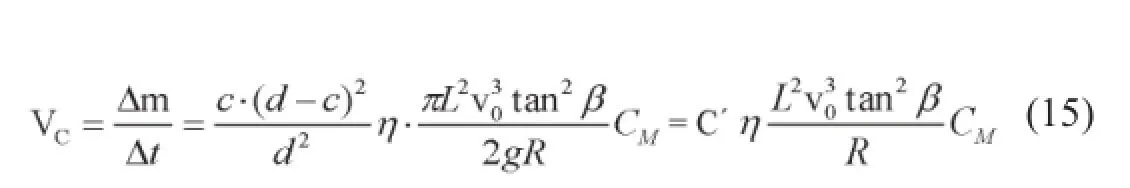
依据阿仑尼乌斯公式[6],C'η是一个与温度有关的函数,用ƒ(T)表示。同时将固定值tan2β和炉膛半径R写入ƒ(T)内,反应速率表达式为

其中:
VC——吹炼阶段炉内的反应速率;
ƒ(T)——与温度有关的函数;
L0——喷嘴与反应液面的临界距离;
L——喷嘴与反应液面的作业距离;
CM——熔体内反应物的浓度;
v0——顶吹转炉转速。
3 生产验证
3.1转速验证
根据第2节计算公式,当压缩空气流量为1200Nm3/h,吹炼温度分别为1373K、1473K和1573K时,绘制不同温度、不同转速时反应速率曲线(见图3)。

图3 转速与吹炼反应速率关系曲线
从图3可看出:随着转速提高,反应速率大幅提高,与转速三次方成正比。生产与数模高度吻合。
3.2喷嘴作业距离验证
当转速、吹炼温度、压缩空气流量分别保持10rpm,1473K、1200Nm3/h,喷嘴到液面的距离分别为100mm、200mm、300mm、400mm时,绘制不同喷嘴作业距离时反应速率曲线(见图4)。
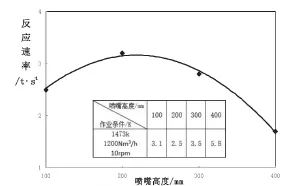
图4 喷嘴作业距离与吹炼反应速率关系曲线
从图4可以看出:喷嘴到反应界面有一个临界距离,当作业距离小于临界距离时,反应速率与距离的平方成正比;反之,反应速率减小,公式不适用。生产与数模高度吻合。
4 结论
对顶吹转炉吹炼过程建立数学模型,研究并验证了吹炼阶段反应速率公式。从验证结果来看,反应速率公式是合理正确的,获得顶吹转炉吹炼阶段较优工艺参数为:转速8 rpm~12 rpm;喷嘴高度
200 mm。
[1]罗庆文. 有色冶金概论[M]. 北京: 冶金工业出版社, 2007.
[2]黎鼎鑫, 王永录.贵金属提取与精炼: 第2版[M].湖南: 中南工业大学出版社, 2001.
[3]邓修, 吴俊生. 化工分离过程[M].北京: 科学出版社, 2000.
[4]傅崇说. 有色冶金原理[M]. 北京: 冶金工业出版社, 1984.
[5]王志魁,刘立英, 刘伟.化工原理: 第4版[M]. 北京: 化学工业出版社, 2010.
[6]梁英教.物理化学: 第2版[M]. 北京: 冶金工业出版社, 1992.

陈志刚(1976-),男,湖北广水人,本科学历,高级工程师,主要从事冶炼技术工作。
E-mail: ahchenzg@163.com
邹贤(1988-),女,陕西汉中人,本科学历,助理工程师,主要从事冶炼技术工作。
E-mail: zoxian@foxmail.com
张源(1957-),男,山西太原人,本科学历,教授级高工,主要从事冶炼技术工作。
E-mail: zhangyuan@tlys.cn
涂百乐(1975-),男,安徽潜山人,冶炼工程师、注册安全工程师,主要从事贵金属生产与研究工作。
E-mail: 1052065772@qq.com
周斌(1990-),男,湖南衡阳人,本科学历,助理工程师,主要从事冶炼技术工作。
E-mail: 1214634860@qq.com
Mathematical Model Study on Reaction Rate of Top-blown Converter Converting Process
Zhigang Chen, Xian Zou, Yuan Zhang, Baile Tu, Bin Zhou(Tongling Nonferrous Metals Rare & Precious Metals Subsidiary Co., Tongling, Anhui, 244021, China)
This paper establishes a mathematical model of top-blown converter converting process in accordance with interface updating theory and thereby engages in research on a formula of top-blown converter converting rate and verify with production data. In practical operation of top-blown converter converting, the model has achieved better technical parameters.
Top-blown Converter; Converting; Reaction Rate; Mathematical Model
TF801.2
A
2095-8412 (2016) 04-621-03
工业技术创新 URL: http://www.china-iti.com 10.14103/j.issn.2095-8412.2016.04.010

