基底完全粗糙时统一强度理论下的极限承载力

沈 君，林光国，王启贵

（1.无锡市政设计研究院有限公司，江苏无锡，214072；2.温州市瓯江口开发建设投资集团有限公司，浙江温州，325026；3.浙江华东工程安全技术有限公司，浙江杭州，311122）



基底完全粗糙时统一强度理论下的极限承载力

沈 君1，林光国2，王启贵3

（1.无锡市政设计研究院有限公司，江苏无锡，214072；2.温州市瓯江口开发建设投资集团有限公司，浙江温州，325026；3.浙江华东工程安全技术有限公司，浙江杭州，311122）

目前大多数地基极限承载力系数公式仍借用Prandtl地基极限承载力的结论，而考虑到计算模型的差异，Nc与Nq之间并不存在Nc=（Nq-1）tanϕ的关系。且实验证明，中间主应力对土体的强度会产生一定的影响，而由Mohr-Coulomb准则推导出的公式并没有考虑中间主应力的影响，致使结果偏于保守。依据极限平衡原理，结合统一强度理论，研究在基底完全粗糙情况下极限承载力的解析解，并通过分析算例，验证了极限承载力解析解的合理性。结果表明在计算过程中加入中间主应力这一影响因素时地基的极限承载力会提高，从而在实际运用过程中充分发挥材料自身的承载能力。

完全粗糙；统一强度理论；极限承载力；解析解

0　引言

地基极限承载力是一个经典课题，理论公式繁多，且大多数地基极限承载力系数公式与Prandtl所采用的计算模型不同，但仍借用Prandtl的结论，即Nc=（Nq-1）tanφ。实验证明，中间主应力对土体的强度有一定影响［1-10］，但基于Mohr-Coulomb准则推导出的公式并没有考虑中间主应力的影响，致使结果偏于保守，不能完全发挥土体的强度潜能。极限承载力理论公式一般形式为［11］：

式中Nγ、Nq、Nc为地基承载力系数。

文献［4］提出了统一强度理论，考虑了中间主应力，并用一个统一的力学模型表述材料的力学性质。

统一强度理论可表示成如下形式［5］：

式中，a=σt/σc，为材料的拉压强度比；b为统一强度理论中反映中间主剪应力及相应面上的正应力对材料破坏影响程度参数；σt为岩土体抗拉强度；σc为岩土体抗压强度。σt、σc、a、b由实验确定。文献［11］得出如下结论：

式中，m=2σ2/（σ1+σ3）；φ0为土体的内摩擦角；φt为统一强度理论下的内摩擦角；c0为土体的粘聚力；ct为统一强度理论下的粘聚力。

1　受力分析

如图1所示，基底完全粗糙，基础底面AE与AB成φt角，滑动线BC是以A为中心的对数螺旋线。

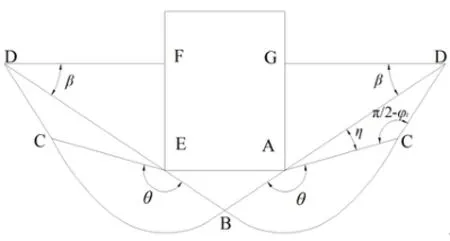
图1　计算简图Fig.1 Calculation diagram

取弹性核ABE为隔离体进行受力分析，如图2所示。

图2　弹性核受力分析Fig.2 Force analysis of the elastic kernel

根据弹性核ABE的静力分析可得：

式中，W为弹性核重量；T为基底宽度；α=φt，为AB与基础底面的夹角；Ep为弹性核两侧面受到的反作用力。

将AB边看作挡土墙墙背，分别计算考虑土重和考虑粘聚力和超载这两种条件下的被动土压力Ep1和Ep2。

2　考虑土重

如图1所示，根据对A点的力矩平衡计算被动土压力Ep1。分别计算ACDG区、对数螺旋线区、CD面上的反力、对数螺旋线破坏面段反力以及静止土压力对A点的力矩（顺时针为正）。

2.1ACDG区对A点力矩Mr1

针对图3分析可得，ACDG区对A点的力矩为

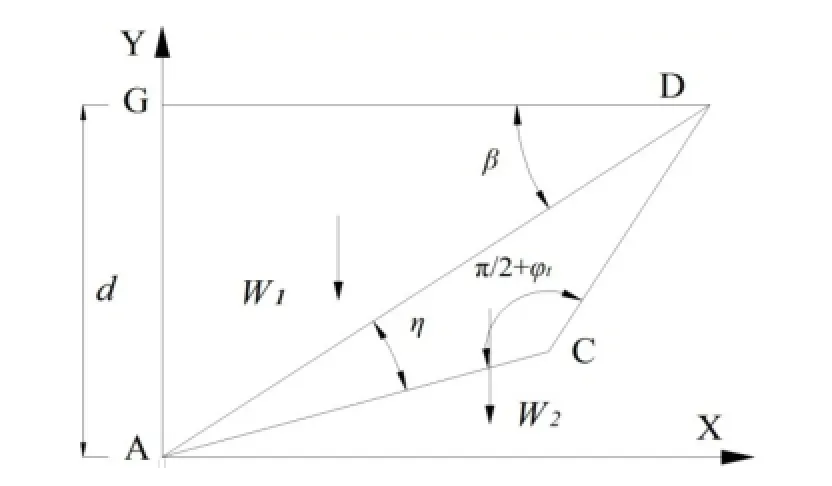
图3　ACDG区分析Fig.3 Analysis of the ACDG area

2.2对数螺旋线区对A点的力矩Mr2

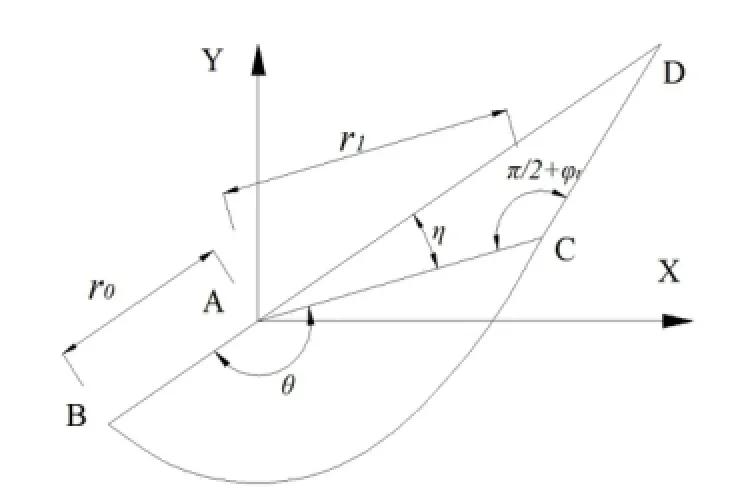
图4　对数螺旋线区分析Fig.4 Analysis of the logarithmic spiral area

如图4所示，对数螺旋线公式为：

式中，θ=180°+β-η-φt。

对数螺旋线区对A点的力矩为：

2.3CD段反力对A点力矩Mr3

如图5所示，由力系平衡可知：

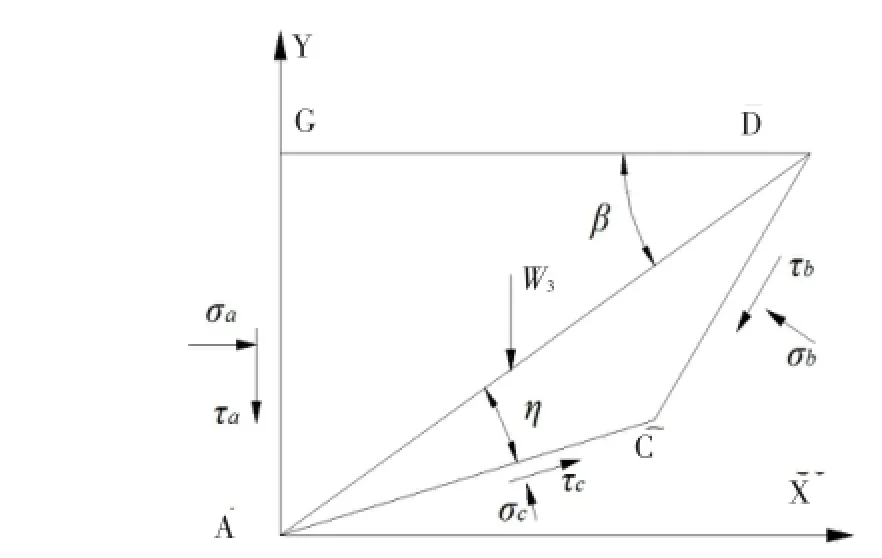
图5　DC边受力分析Fig.5 Force analysis of the DC side

2.4对数螺旋线破坏面段反力对A点的力矩Mr4

由对数螺旋线的性质可知，当处于极限平衡状态时，对数螺旋线破坏面上的合力通过中心点A点，因此对数螺旋线破坏面段反力对A点的力矩Mr4=0。

2.5AG段静止土压力对A点的力矩Mr5

根据以上分析，AG段静止土压力的合力R2方向与AG的法线成δ角，力矩Mr5=0.5σad2。

3　考虑粘聚力和超载

根据被动土压力理论，土的粘聚力CD面上产生的被动土压力呈矩形分布，被动土压力Ep2对于A点的力臂为0.25T。

3.1BC螺旋线下粘聚力对A点的力矩Mr1′

根据对数螺旋线的性质，对数螺旋线下粘聚力对A点的力矩为：

3.2CD面段粘聚力对A点的力矩Mr2′

分析可知CD面段粘聚力对A点的力矩为：

4　极限承载力公式求解

根据对A点的力矩平衡可得：

将上式代入弹性核公式（4），可得极限承载力的解析式：

式中：

其中β值求解与Meyerhof公式中的方法类似，在此不做赘述。

5　算例分析

温州某地区有一宽为4 m的条形基础，埋深3 m，地基为均质粘性土，其容重γ=19.5 kN /m3，固结不排水抗剪强度指标为c0=20 kPa，φ0=22°。设土的静止侧压力系数K0=0.45，基础与土之间的摩擦角δ=12°。下面分别用太沙基公式、双剪强度理论、文中公式求地基极限承载力。

5.1利用太沙基公式

假定基底完全粗糙，由φ0=22°可得，Nc=20，Nq=10，Nγ=7，由此太沙基极限承载力为：qu=1 258 kPa。

5.2利用双剪强度理论

假定基底完全粗糙，由φ0=22°可得，Nc=27.5，Nq=14.78，Nγ=12.3，由此得地基极限承载力为：qu= 2 017.7 kPa。

5.3利用本文公式

当系数m=1，假定b（0≤b≤1）取不同数值，利用文中公式分别求其地基极限承载力。

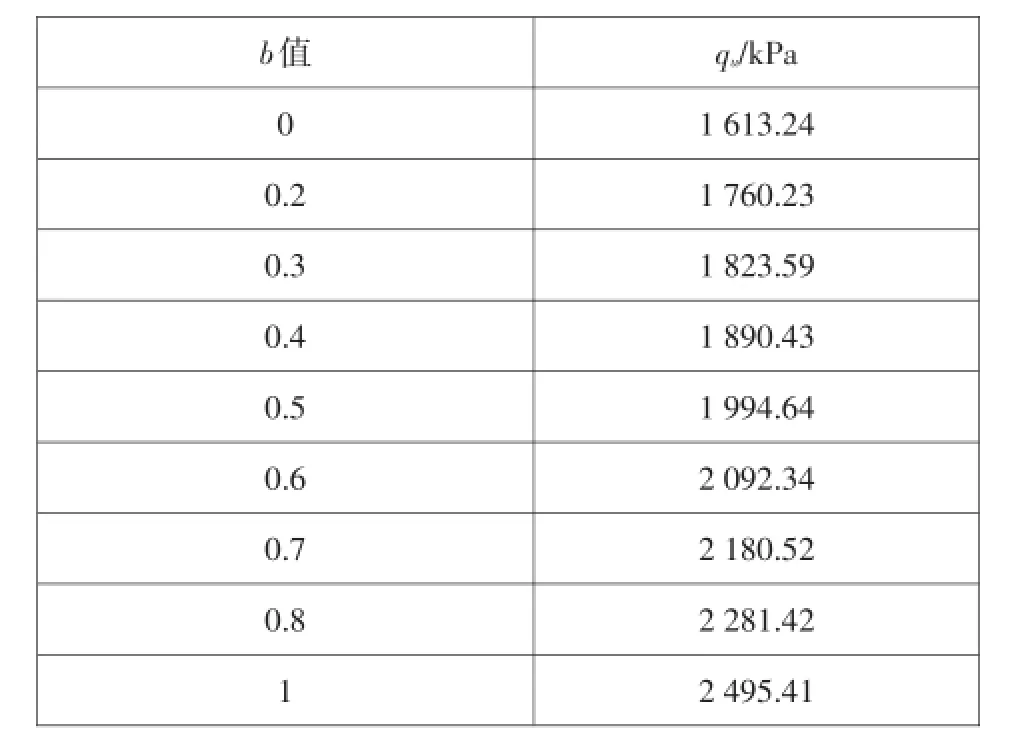
表1　基底完全粗糙时极限承载力Table 1 The ultimate bearing capacity with completely coarse foundation base

图6　qu与参数b关系图Fig.6 The relation between quand b

由以上计算结果可知，基底完全粗糙时，文中计算公式相对于太沙基公式和双剪强度理论计算得到的极限承载力较高，且地基极限承载力的计算值随着中间主应力系数b值的增大而显著增大，说明中间主应力对地基承载力有一定影响。

6　结语

随着中间主应力系数b值的增大，地基极限承载力越大，说明中间主应力对地基极限承载力有一定影响。

结合统一强度理论的计算方法能使地基极限承载力的计算值提高，在某种程度上更确切地反映了地基极限承载力的实质，能充分发挥材料自身的承载能力。

［1］陈仲颐，周景星，王洪瑾.土力学［M］.北京：清华大学出版社，1994.

［2］钱家欢，殷宗泽.土工原理与计算［M］.北京：中国水利水电出版社，1995.

［3］商建林，涂长红，谢叶彩.地基极限承载力确定方法的分析与评价［J］.西部探矿工程，2007（2）：140-142.

［4］俞茂宏.双剪理论及其应用［M］.北京：科学出版社，1998.

［5］俞茂宏.岩土类材料的统一强度理论及其应用［J］.岩土工程学报，1994，16（2）：1-10.

［6］周小平，王建华.考虑中间主应力影响时条形基础极限承载力公式［J］.上海交通大学学报，2003，36（4）：552-555.

［7］Michelis P.Polyaxial yielding of granular rock［J］.Journalof Engineering.Mechanics ASCE，1985，111（8）：1049-1066.

［8］Vesic A S.Expansion of cavities in infinite soilmass［J］.Soil Mechanics and Foundations Division，ASCE，1972，98（3）：265-267.

［9］Mogi K.Fracture and flow of rocks under high triaxial compression［J］.Journal of Geophysical Research，1971，76（5）：1255-1269.

［10］周小平，张永兴.利用统一强度理论求解条形地基极限承载力［J］.重庆大学学报，2003，26（11）：109-112.

［11］沈珠江.理论土力学［M］.北京：中国水利水电出版社，2000.

［12］周小平，张永兴.基于统一强度理论的太沙基地基极限承载力［J］.重庆大学学报，2004，27（9）：133-136.

Most of the formulas for foundation ultimate bearing capacity factor are still borrowing the results of Prandtl theory.Considering the difference of calculation models，Nc=（Nq-1）tanϕ is not true.And experiments have proved that the intermediate principal stress would produce some influence to strength of soil.The result derived from Mohr-Coulomb criterion formula doesn't consider the effect of intermediate principal stress which causes the conservative results.To solve these problems，according to ultimate balance theory and unified strength theory，the analytical formulas of ultimate bearing capacity with completely coarse foundation is studied.In the calculation process，the intermediate principal stress factors is considered which results in a higher ultimate bearing capacity of foundation.Thus，in the practical application，the bearing capacity of the material itself can be fully utilized.

completely coarse；unified strength theory；ultimate bearing capacity；analytical formula

TV222.2

A

1671-1092（2016）02-0041-04

2015-07-13

沈 君（1984-），男，湖北襄阳人，工程师，从事市政道桥设计及工程管理工作。

作者邮箱：wang_qg@ecidi.com

Title：Ultimate bearing capacity based on unified strength theory with completely coarse foundation base//by SHEN Jun，LIN Guang-guo and WANG Qi-gui//Wuxi Municipal Design Institute Co.，Ltd.