基于随机前沿分析模型的河南省小麦生产技术效率测算与评价
董奋义,介宇扬,韩咏梅,马新明,李炳军
(河南农业大学信息与管理科学学院,河南 郑州 450046)
基于随机前沿分析模型的河南省小麦生产技术效率测算与评价
董奋义,介宇扬,韩咏梅,马新明,李炳军
(河南农业大学信息与管理科学学院,河南 郑州 450046)
本研究考虑到天气、病虫害等不确定性因素的影响,采用随机前沿分析方法,对河南省豫北、豫西、豫南、豫中东等4个区域,基于2000—2014年河南省小麦生产的相关数据,测算和比较不同区域和各地市小麦生产的技术效率。结果表明,在计算期内河南省小麦生产的平均技术效率值达到0.79,18个地市的技术效率值范围在0.34到0.99之间,存在明显的区域差异,从而得出河南省小麦生产处于规模报酬递增阶段,而劳动力的产出弹性系数为负的结论。
河南省;小麦生产;技术效率;随机前沿分析
河南省是中国农业大省和粮食生产大省,多年来其小麦产量一直占全国的1/4以上,为国家粮食安全做出了突出贡献。科技进步在农业和粮食生产中起着重要作用。SCHULTZ[1]的研究表明,美国战后农业生产的增长中80%是由科技进步引起的。技术效率是衡量科技进步的重要指标,它反映了生产中对现有资源有效利用的能力。随着工业化和城市化的快速发展,小麦产量的提高不能仅仅依靠有限的耕地面积和物质投入,如何提高技术效率才是关键[2]。目前关于河南省小麦生产技术效率的相关测算还没有涉及到地区分类或者各个地市层面上,对河南省不同地市小麦生产技术效率的计算、分析和比较,有利于促进农业资源的优化配置,保证小麦高产稳产,保障粮食充分供给,加快农业现代化进程的实现。对河南省小麦生产的技术效率进行研究,考虑到天气、病虫害等不确定性因素对小麦生产的影响,采用随机前沿分析方法进行定量研究,为规范发展河南省小麦生产和正确引导小麦生产科技投入,提供决策理论依据。
1 国内外研究文献
测算技术效率的常用方法是生产前沿分析。生产前沿指在技术水平一定的情况下,各种投入比例所对应的最大产出集合。前沿分析方法可以分为参数方法和非参数方法,前者常用的是随机前沿分析(Stochastic Frontier Analysis,简称SFA),后者常用的是数据包络分析(Data Envelope Analysis,简称DEA),SFA的最大优点是考虑了不确定性因素对于产出的影响。KOOPMANS[3]、DEBREU[4]和SHEPHARD[5]的研究对SFA领域产生了直接的影响。MEEUSEN等[6]、AIGNER等[7]先后发表的两篇文章成为SFA发展的起点。
FARE等[8]认为技术效率是在相同的产出下生产单元理想的最小可能性投入与实际投入的比率,并首次实证测算了技术效率。LEIBENSTEIN[9]从产出角度指出技术效率是在相同的投入下生产单元实际产出与理想的最大可能性产出的比率。KUMBHAKAR[10-11],BATTESE等[12]等利用面板数据模型测度了技术效率。常用测度技术效率的方法中,超越生产函数和随机前沿分析方法的结合更加符合经济学理论的假设,它不仅可以根据实际需要加入虚拟和代理变量,还具有很强的稳定性。
近年来,国内使用SFA测算农业生产技术效率的研究文献逐渐增多。赵芝俊等[13]运用超越对数随机前沿模型测算出中国农业技术效率为0.81。姚增福等[14]测算出2000—2007年间13个粮食主产区平均技术效率为0.68。田伟等[15]采用1995—2008 年中国13个棉花主产区的面板数据,测算并聚类分析了各省棉花生产的技术进步率。孙炜琳等[16]等对2004—2011年全国18个淡水养殖省份的技术效率进行了随机前沿分析方法的测算,结果显示样本省份淡水养殖平均技术效率均在0.9以上。贾筱智等[17]计算出1995—2003年间中国小麦生产的技术效率在0.8以上进行波动,2003—2009年期间呈现出快速增长的趋势。苗珊珊[18]对2000—2011年间15个小麦主产区面板数据进行了随机前沿分析,将技术进步分为生化技术进步和机械技术进步两种,得出小麦单产的平均技术效率值达到0.87。孙昊[19]测算出 2001—2010年间中国小麦单产的平均技术效率达到0.86。夏海龙等[20]基于2005—2008年间农户的截面调查数据得出河南省小麦生产的技术效率的范围为0.77~0.87。效赛丽等[21]利用2003—2013年河南省18个地区粮食投入产出数据,研究河南省粮食生产的全要素生产率及其变动特征。
本研究把河南省定性分为豫北、豫西、豫南和豫中东4个区域,使用2000—2014年河南省18个地市的270个面板数据,建立超越对数生产函数的随机前沿分析模型,对河南省4个区域和各地市小麦生产中的技术效率进行测算和比较研究,并提出相应的政策建议。
2 模型构建和数据来源
BATTESE等[22]建立的随机前沿函数的一般形式为:
Yit=βXit+vit-μit(i=1,2,…,n)
(1)
式中的Yit是第i个生产单元第t年的产出,Xit为第i个生产单元第t年的要素投入。
根据已有的数据和思路,本研究所建立的基于超越对数函数的随机前沿分析模型可表示为:
(2)
式中β项为待估计参数,Yit,Fit,Lit,Mit分别是第i个地区第t年的小麦产量、物质消耗、劳动力投入和播种面积。由于地市级小麦生产的物质消耗数据Fit不易获得,因此,本研究使用小麦生产过程中投入的化肥折纯量来代替,Lit表示农业生产乡村从业人员中用于小麦生产的部分。Fit和Lit均是通过相应数据与小麦播种面积占比相乘得到。
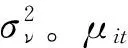
根据袁开智[12]建立的模型求出3种投入要素产出弹性的公式为:
εF=(β1+βA1t)+(β12LnLit+β13LnMit)+
β11LnFit
εL=(β2+βA2t)+(β12LnFit+β23LnMit)+
β22LnLit
εM=(β3+βA3t)+(β13LnFit+β23LnLit)+
β33LnMit
(3)
式中,化肥折纯量产出弹性中的β1+βA1t代表随技术进步变动部分,β12LnLit+β13LnM归为要素相互影响部分,β11LnFit是要素自我强化(抵消)部分,劳动力和播种面积弹性系数的计算与此相似。
假设δ0为随机变量,mit为效率损失函数,e-mit是第i个生产单位在第t年的技术效率水平,技术效率值越大,技术无效率程度越低。Zjit为第j个影响生产无效率的外生变量,效率损失函数模型的计算公式为:
(4)
式中δ0到δj为待估参数,直接反映了各参数对技术效率的影响。
影响小麦生产无效率的因素很多,由于河南省各地市成灾比例相关随机不可控因素数据的缺失,所以本研究选取的可控因素包含:小麦播种面积占比(ARit)、小麦农药使用量(万t,PAit)、农村居民人均纯收入(万元,NIRit)。另外,河南省各地市自然资源条件不同,区域特征也可能成为影响小麦生产效率损失的因素,使得小麦产量发生显著的差异。因此,本研究设定4个虚拟变量来代表不同的区域特征,分别为豫北(D1)、豫西(D2)、豫南(D3)和豫中东地区(D4),则有:
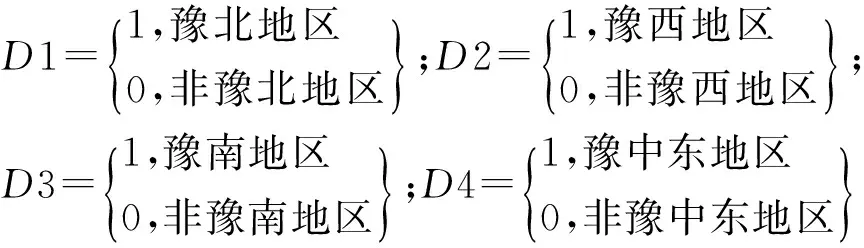
由此,河南省小麦生产的效率损失函数为:
(5)
本研究使用极大似然估计法计算公式(2)和(4)中的未知参数,依据BATTESE[11]提出的简化模型可知:
(6)
(6)式中的γ反应了误差中技术效率损失因素所占的比例。
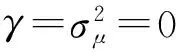
TEit=E(Yit|μit,Xit)/E(Yit|μit=0,Xit)
(7)
μit的值介于0和1之间。当μit=0且TEit=1时,生产单元i处于完全的技术效率状态。当μit=且TEit=0时,生产单元i处于完全的生产无效率状态。
本研究所采用的数据均来自于《河南省统计年鉴》和《中国统计年鉴》。
3 结果与分析
根据数据的整理和分析,河南省小麦生产技术效率测算模型中相关变量的统计情况如表1所示。基于公式(2)和(5),使用软件Frontier 4.1,可得模型回归和效率损失函数的结果如表2所示。
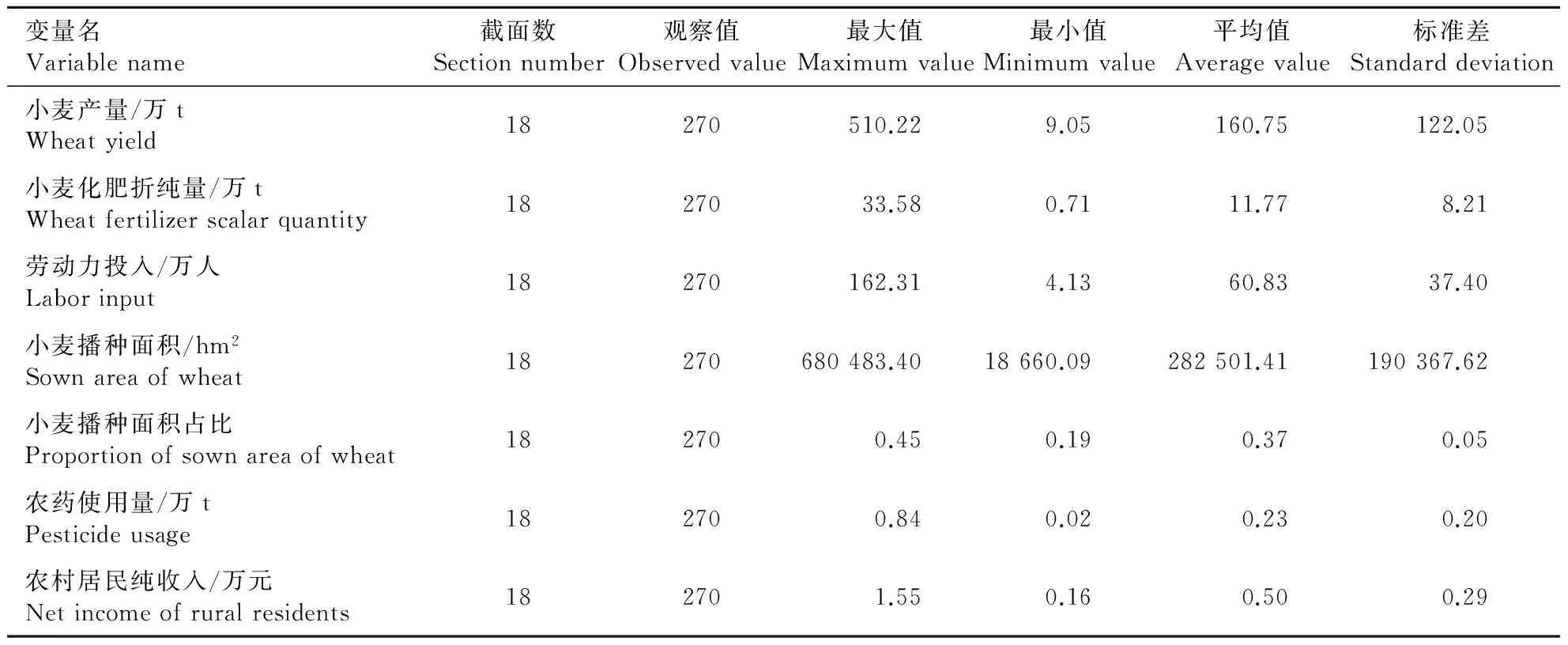
表1 河南省小麦生产相关变量的统计情况Table 1 Statistical information about related variables of wheat production in Henan Province
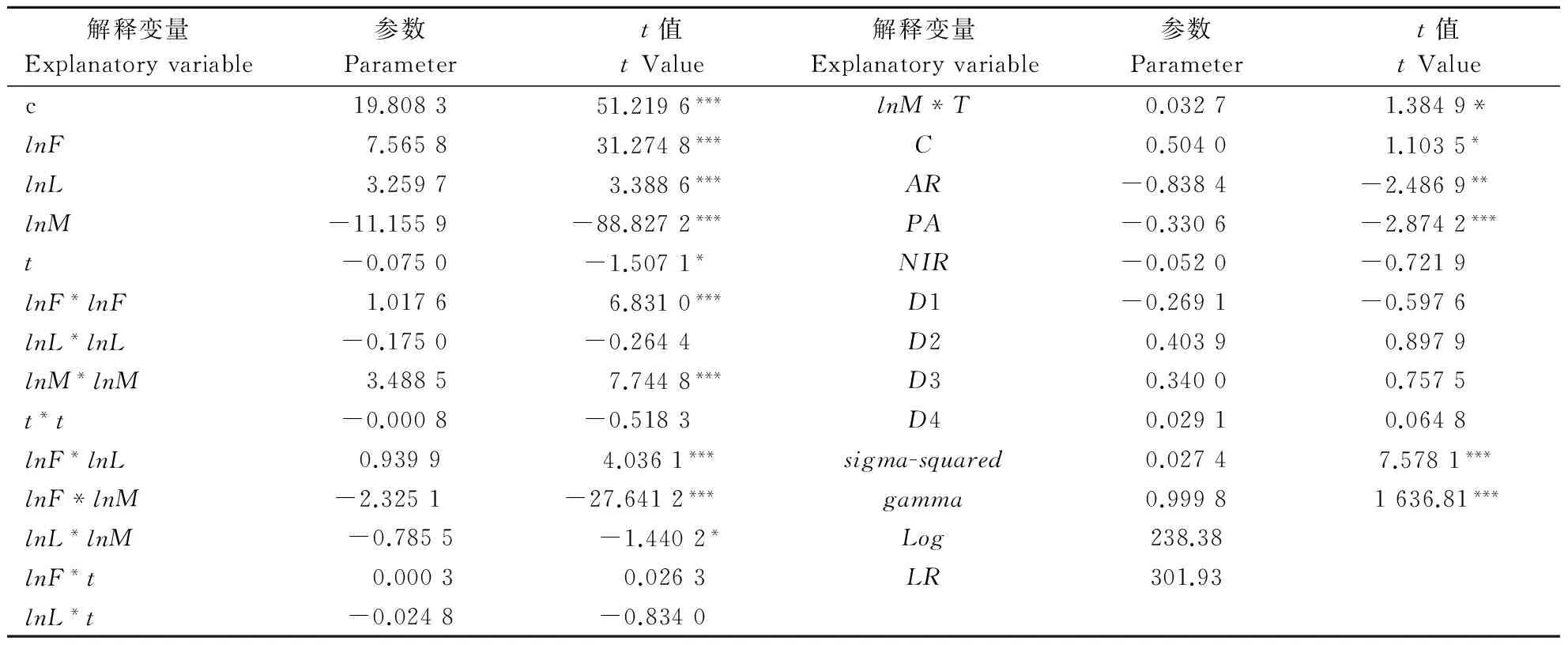
表2 小麦生产随机前沿分析模型和效率损失函数的估计结果Table 2 Estimated results of SFA model and efficiency loss function on wheat production
注:*、**和***分别表示通过10%、5%和1%水平的显著性检验。
Note: *、** and * indicated respectively significant at 10%,5% and 1%.
由表2的统计结果可知,sigma-squared的值为0.027 4,达到了1%的显著水平。gamma值接近于1,表示存在的显著误差主要来自于技术无效项,各地市的小麦实际产出和最大可能产出之间的差距主要是技术作用程度的差异。表中t的系数为负,说明随着时间的推移,小麦的产量可能存在减少的状况。t2的系数也为负,且不显著,表明技术进步率不但没有增长,反而略有放缓。时间变量与劳动力乘积的系数为负,与小麦生产投入的化肥折纯量、播种面积乘积的系数为正。可知,减少劳动力的使用有利于技术进步,河南省小麦生产的技术变化呈现出劳动力耗费、化肥和土地节省的现象。因此,河南省小麦生产不是劳动密集型,而是土地和资本密集型。
在交叉项中,lnM与其他要素的系数均为负,说明播种面积在小麦生产中具有特殊的作用。即小麦生产的土地投入对其他的投入要素具有替代效应,并且对化肥等资本要素的替代作用要大于对劳动力的替代作用。化肥折纯量与劳动力是显著的正相关,表示二者是互补关系。无效率损失函数的估计结果中,小麦播种面积和小麦农药投入对效率损失的作用为负,并且结果检验显著。因此,提高小麦播种面积在农作物播种面积中的比例,增加化肥等物资投入,可以提高小麦生产的技术效率。区域虚拟变量的检验结果均不显著。
在(3)式的基础上,可得出3种投入要素的产出弹性系数如表3所示。表3中各投入要素的弹性之和大于1,说明河南省小麦生产处于规模报酬递增阶段。劳动力的产出弹性始终为负,并且呈现波动趋势,2010—2014年降低趋势明显,这可能是因为农业机械化的发展,取代了一部分劳动力的缘故。河南省小麦播种面积的平均产出弹性系数大于1,说明耕地面积增加带动了小麦产量的增加,而土地属于不可稀缺的有限性资源,河南省是人口大省,人均耕地面积较低,2013年仅达到0.08 hm2·人-1,所以坚守耕地红线对河南省小麦生产具有十分重要的意义。
根据(7)式可以计算出河南省各地市的平均技术效率和技术效率的年平均变化率,测算结果如表4所示。
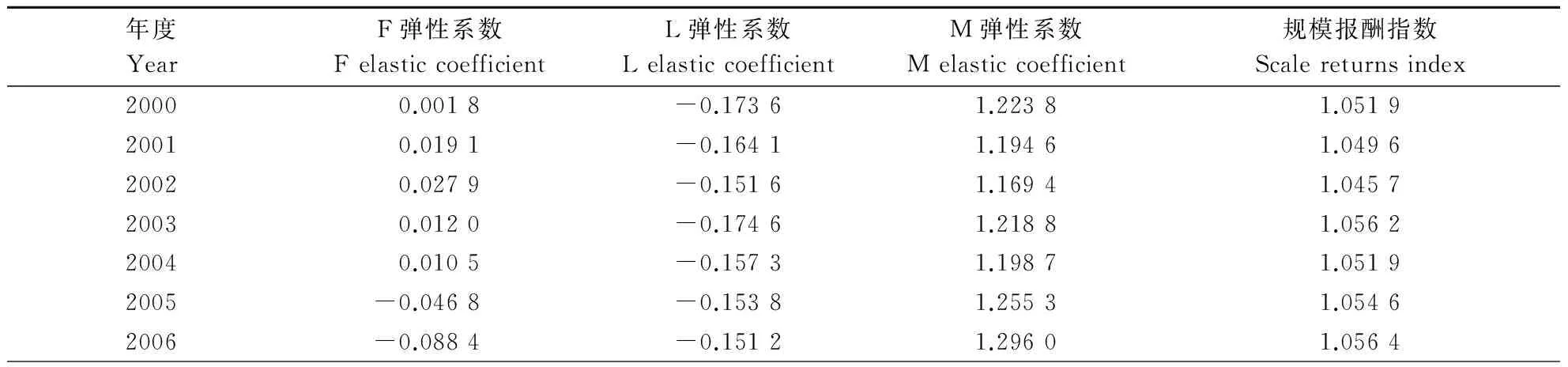
表3 河南省小麦生产投入要素的产出弹性Table 3 Input factors output elastic coefficients of wheat production in Henan Province
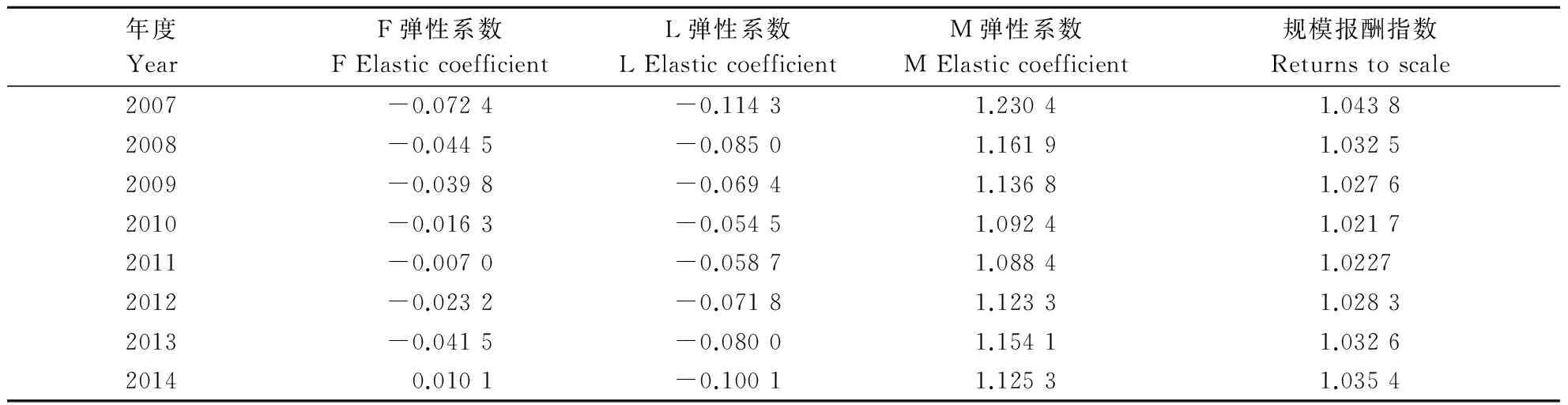
续表 ContinedTable
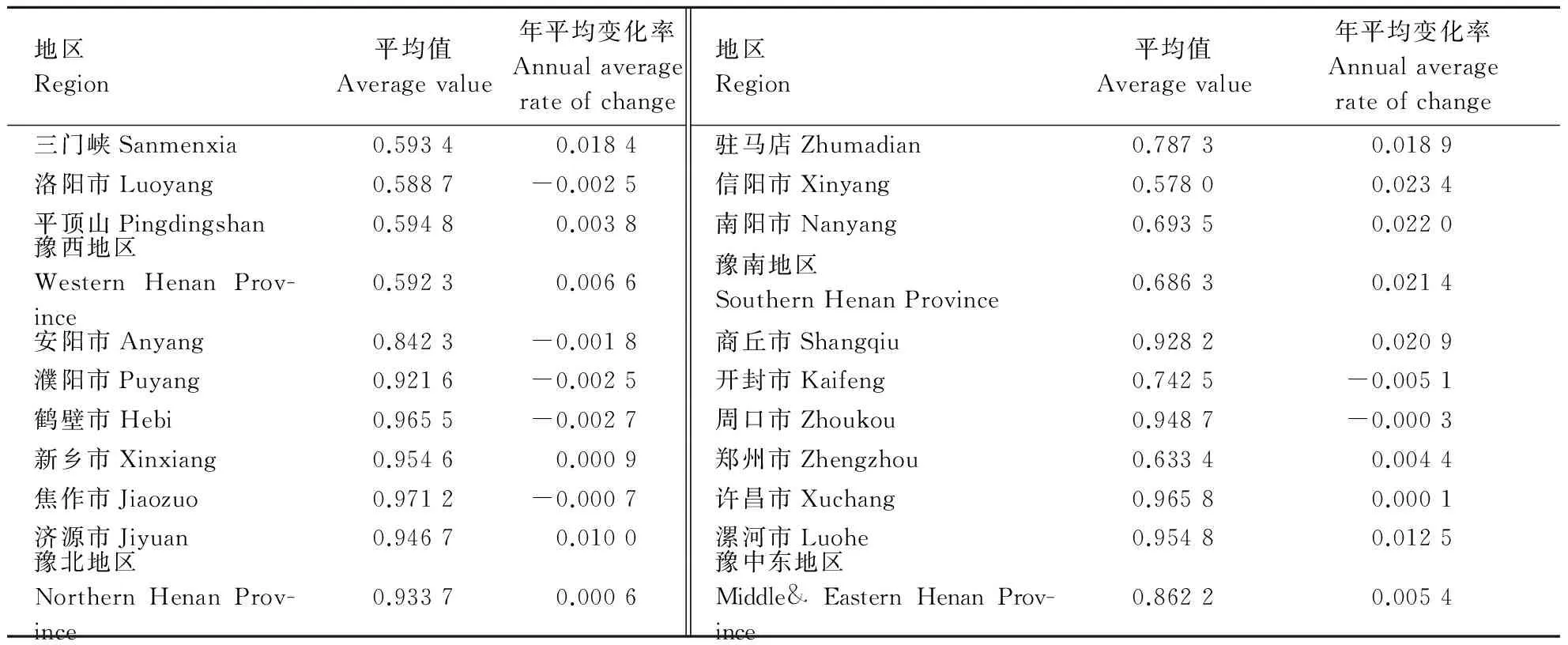
表4 河南省各地市小麦生产的平均技术效率Table 4 Average technical efficiency of wheat production in each area of Henan Province
从地市的角度出发,技术效率随着时间的变化而变化。信阳市2000年小麦生产的技术效率值为0.43,具有起点低,增速快的特点。南阳市和商丘市的技术效率年平均增长率则分别达到2.20%和2.09%。豫南地区的技术效率增长率要高于其他城市。一些地市的技术效率相比2000年不仅没有增加,还有所下降。例如:鹤壁市、焦作市、濮阳市、洛阳市、开封市和周口市。从区域的角度出发,豫南和豫西两个地区小麦生产的技术效率平均值较低,其他两个区域的技术效率较高。同一区域不同地市之间也存在差别。豫西地区平顶山市的技术效率值高于洛阳市和三门峡市。豫南地区各地市的技术效率差别不大,其中驻马店市小麦生产的平均技术效率为0.78,南阳市为0.69,信阳市的技术效率平均值在样本期间内只达到了0.58。河南省中东地区小麦生产的技术效率平均值为0.86,许昌市15年间的技术效率均在0.91以上,而郑州市的技术效率最高值仅达到0.66。
4 结论
样本期间内,河南省小麦生产的平均技术效率为0.79,年均变化率为0.49%,说明河南省小麦生产的技术利用较为充分,但还具有一定的提升空间。挖掘现有技术潜力可以改进生产效率,政府应加大科研投入,推动互联网、物联网、云计算、遥感等现代信息技术与小麦生产活动相结合,建立技术成果转化激励机制,完善技术推广体系,促进技术效率的提高。
研究结果显示,劳动力的产出弹性系数为负,符合现实情况中劳动力逐年递减的情况。各地市的要素弹性不同,但总体上小麦播种面积的弹性系数均为正值,说明小麦生产依赖于土地。农民是新信息的接受者和新技术的使用者,培养一批高知识、高素养、高技能的新型农民势在必行。政府应坚守小麦耕种面积红线,鼓励劳动力转移,在普及基础教育的基础上,大力建设县乡职业农民技术培训机构[23]。另外,根据不同地市的生产条件和技术效率利用状况,政府应该因地制宜地采取不同的措施。譬如,豫南地区的驻马店、信阳和南阳具有较好的农业基础,始终处于规模报酬递增阶段,可以扩大小麦生产规模,增加机械技术方面的资金投入和补贴力度,以提高小麦生产技术效率。河南省需要完善基础设施,加快小麦生产的机械化和规模化,实现小麦生产的稳定增长。
[1] SCHULTZ T W. Institutions and the rising economic value of man [J]. American Journal of Agricultural Economics, 1968, 50(5):1113-1122.
[2] 徐峥,陈书章,朱琰洁,等.河南省小麦生产综合技术效率及要素投入动态优化分析[J]. 河南农业大学学报,2012,46(5):589-595.
[3] KOOPMANS T C. Efficient allocation of resources[J]. Econometrica, 1951, 19(4):455-465.
[4] DEBREU G.The coefficient of resource utilization[J]. Econometrica, 1951, 19(3):273-292.
[5] SHEPHARD R W. Cost and production functions: lecture notes in economics & mathematical systems[M].Berlin:Springer-Verlag.1981:194.
[6] MEEUSEN W, BROECK J V D. Efficiency estimation from cobb-douglas production functions with composed error[J]. International Economic Review, 1977, 18(18):435-44.
[7] AIGNER D, LOVELL C A K, SCHMIDET P. Formulation and estimation of stochastic frontier production function models[J]. European Journal of Clinical Pharmacology, 1977, 6(1):21-37.
[8] FARE R, LOVELL C A K, FARE R, et al. Measuring the technical efficiency Of production[J]. Journal of Economic Theory, 1978, 19(1):150-162.[9] LEIBENSTEIN H. Allocative efficiency Vs x-efficiency[J]. American Economic Review, 1966, 56(3):392-415.
[10] KUMBHAKAR S C. Production frontiers, panel data, and time-varying technical inefficiency[J].Journal of Econometrics, 1990, 46(1/2):201-211.
[11] KUMBHAKAR.The measurement and decomposition of cost-inefficiency: the trans-log cost system[J]. Cancer Research, 1991, 43(4):667-83.
[12] BATTESE,G E,COELLI,T J. Frontierproduction functions, technical efficiency and panel data: with application to paddy farmers in India[J]. Journal of Productivity Analysis, 1992, 3: 153-169.
[13] 赵芝俊,袁开智.中国农业技术进步贡献率测算及分解1985-2005 [J]. 农业经济问题,2009,(3):28-36.
[14] 姚增福,郑少锋.我国粮食主产区粮食生产技术效率进步与效率损失测度[J].电子科技大学学报(社科版),2010(6):24-28.
[15] 田伟,李明贤,谭朵朵.中国棉花生产技术进步率的测算与分析—基于随机前沿分析方法[J]. 中国农村观察,2010,(2):45-53.
[16] 孙炜琳,刘佩,高春雨. 我国淡水养殖渔业技术效率研究—基于随机前沿生产函数[J]. 农业技术经济,2014,(8):108-117.
[17] 贾筱智,郭亚军,许立.我国小麦生产技术进步率的测算及分析—基于随机前沿分析方法[J].广东农业科学,2013,(2):192-196.
[18] 苗珊珊.我国小麦生产的技术效率和技术进步模式[J]. 华南农业大学学报(社会科学版),2014,(3):9-17.
[19] 孙昊.小麦生产技术效率的随机前沿分析—基于超越对数生产函数[J]. 农业技术经济,2014,(1):42-48.
[20] 夏海龙,郭燕枝,郭静利.农户小麦生产的产出增长与分解—基于河南省农户层面的实证分析[J]. 中国农业科学,2012,(3):569-574.
[21] 效赛丽,朱秀英,赵亚娟,等.基于SFA的河南省粮食生产全要素生产率分析[J]. 河南农业大学学报,2015,49(6):861-865.
[22] Battese G E, Coelli T J, A Model for technical inefficiency effects in a stochastic production frontier for panel data[J]. Empirical Economics, 1995,20 (2),325 -332.
[23] 朱帅蒙,陈伟强,程道全,等.河南省可实现粮食生产潜力研究[J].河南农业大学学报,2016,50(1):115-121.
(责任编辑:马红春)
MeasurementandevaluationoftechnicalefficiencyofwheatproductioninHenanProvincebasedonSFAmodel
DONG Fenyi, JIE Yuyang, HAN Yongmei, MA Xinming, LI Bingjun
(College of Information and Management Science, Henan Agricultural University, Zhengzhou 450046, China)
Taking into account the uncertain factors such as weather, diseases and insect pests, and using the method of stochastic frontier analysis,this paper established the stochastic frontier analysis model with the trans-log production functions, and the technical efficiency of wheat production in the northern, western, southern and the middle east region, based on the input and output data of wheat in 18 cities of Henan Province in 2000—2014 were analyzed. Its value in different regions and cities were also calculated and compared. The results showed the mean value of technical efficiency of wheat production achieved 0.79 during the sample period. The range of technical efficiency for 18 cities is around 0.34 and 0.99, which exerts obvious regional differences. This paper comes to the conclusion that wheat production was at the stage of increasing returns to scale in Henan Province, while the output elasticity coefficient of labor force was negative.
Henan Province; wheat production; technical efficiency; stochastic frontier analysis
2015-04-14
国家自然科学基金项目(41171444);河南省高等学校重点科研项目(15A630032)
董奋义(1972-),男,河南平舆人,副教授,博士,从事灰色系统理论、决策分析等方面的研究。
马新明(1963-),男,河南许昌人,教授,博士,博士生导师。
1000-2340(2016)06-0831-06
F303
:A

