滦河上游年降水量多时间尺度变化的EEMD分析

张小鹏

滦河上游年降水量多时间尺度变化的EEMD分析

张小鹏

（山西水利职业技术学院，山西运城044004）

以多伦气象站1956—2014年的年降水量序列为代表，运用EEMD方法分析了滦河上游年降水量的多时间尺度变化特性。结果表明，滦河上游年降水量具有准2～4年、准4～6年、准10年、准15～20年波动周期，整体变化呈衰减趋势。

滦河上游；多伦；年降水量；多时间尺度；EEMD；衰减；最严格水资源管理制度

滦河是海河流域的一条重要水系，发源于河北省丰宁县大滩镇，经沽源县向北流入内蒙古多伦县境，至外沟门子又进入河北省境内，蜿蜒于峡谷之间，到潘家口越长城，经滦县进入平原，于乐亭县境内注入渤海，全长888 km，流域面积4.47万km2。自河源至张百湾为上游，自张百湾至滦县为中游，滦县至入海口为下游。

气象系统是复杂的非线性动力学系统，作为其重要输出变量，降水量的年际变化存在着多时间尺度性，即年降水量序列在某一时间段内不是只以一种固定的频率（时间尺度、周期）在运动，而是同时包含着各种频率（时间尺度、周期）的变化和局部波动［1］，是多种动力机制同时在发挥作用，使得气象系统变化在时域中存在着多层次的时间尺度和局部化特征。作为水文水资源系统中的最活跃的基本输入变量，降水量的变化对于流域水资源量的形成和分布具有重要影响。

笔者采用EEMD方法分析滦河上游的多伦气象站近60年来年降水量的多时间尺度变化特性，以期为评价滦河流域水资源情势、制定水量分配方案以及贯彻落实最严格水资源管理制度等工作提供科学参考。

1　数据和方法

1.1数据

本分析采用位于滦河上游的多伦县气象站1956—2014年的年降水量序列，如图1所示。

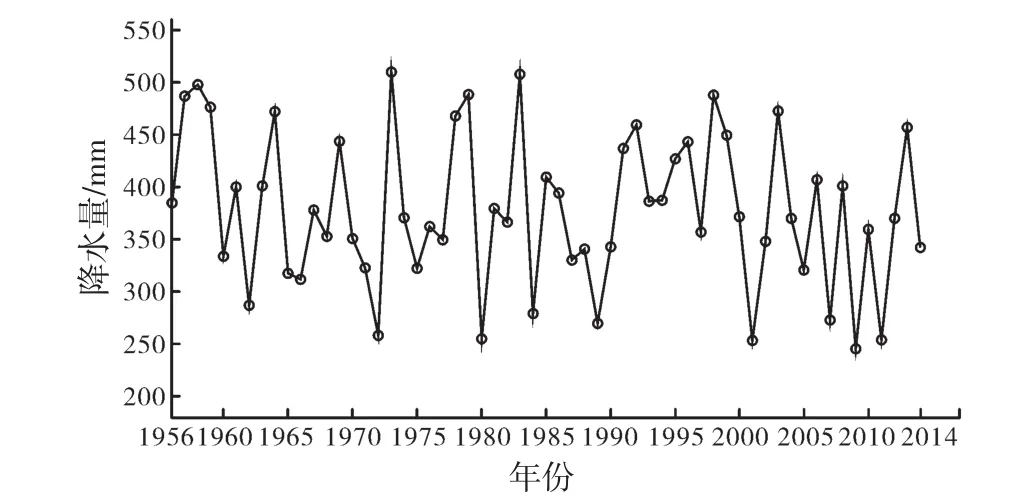
图1　多伦站年降水量序列

1.2方法

就其实质而言，小波变换是一种窗口可调的傅立叶变换，它要求在小波窗内所分析的信号必须是平稳的，小波变换会造成很多虚假的谐波，基函数的选择对小波分解结果有显著影响［2］。为此，Huang等人提出了经验模态分解（Empirical Mode Decomposition，EMD）方法［3］，该方法是基于信号的局部特征时间尺度从原信号中提取一系列的幅度和频率都经过调制的函数，这些函数称之为本征模态函数（Intrinsic Mode Function，IMF），原始信号可以用本征模态函数之和来进行还原和表达，各IMF分量包含了原始信号的不同时间尺度局部特征信息，具有明显的物理背景，而其中最低频率的IMF分量通常代表原始信号的趋势或均值。但是，EMD方法在分解过程中容易产生混频即模态混叠或称尺度混合现象，为此Huang等人又对EMD方法进行了改进，提出了集合经验模态分解（Ensemble Empirical Mode Decom-position，EEMD）方法［4］，具体是通过向原信号中多次添加不同的白噪声之后再分别进行EMD分解，然后再对经过多次EMD分解所得的各个IMF分量分别求平均值而得到最终的实际分量。EEMD方法通过多次集合平均来抵消白噪声的影响，可以有效地改善EMD方法所存在的模态混叠现象。

EEMD方法的具体计算步骤为：首先将给定振幅的白噪声序列叠加在待分解的数据序列上，形成混合序列，然后再对此混合序列进行EMD分解。如此反复，每次加入振幅相同的新的白噪声序列都会得到不同的IMF分量，最后，将各次分解得到的IMF分量进行集合平均以作为相应IMF分量的最终分解结果。

EMD方法中的本征模态函数（IMF）要满足以下2个条件：①在整个数据范围内，过零点和极值点的数量必须保持相等或至多相差1；②在任何点处，所有极大值点形成的上包络线和所有极小值点形成的下包络线的平均值始终保持为0。某一信号可以进行EMD分解的前提为：①被分解的信号至少存在2个极值点：1个极大值点和1个极小值点；②局部特征时间尺度可定义为信号中两临近极大值点或极小值点的时间间隔；③若信号中不存在极值点，但包含若干拐点，可以先对信号进行若干次微分，使得极值点显露出来后，再对分解得到的分量进行积分来求得最后结果。

EMD分解的基本思想是：若加入待分解数据序列的极小值或极大值数目比下跨零点（或上跨零点）的数目多2个或2个以上，则该数据序列需要进行平稳化处理。平稳化处理时，首先，利用三次样条函数把序列x（t）的局部极小值点和局部极大值点分别拟合成x（t）的下包络线和上包络线，然后再计算2条包络线的平均值m1。再从原始数据序列x（t）中减去m1，即可得到一个移除了低频信号的新的数据序列：

通常，h1并不是IMF分量，为此尚需对h1重复以上处理过程以进行k次筛选直至所得到的包络平均值趋于零为止，此时所得数据为：

式中：h1k为第k次筛选所得的数据；h1（）k-1为第k-1次筛选所得的数据。可使用限制标准差SD的值来判断每次所得的筛选结果是否为IMF分量，SD定义为：

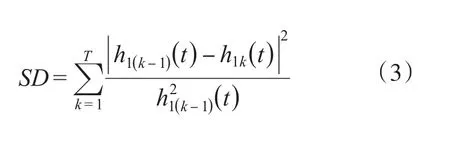
式中：T为数据序列长度；其他变量含义同前。

一般地，SD值取0.2～0.3，即满足0.2〈SD〈0.3时，EMD分解过程即可结束，这样既使得hk（）t足够接近IMF的要求，又可以控制分解的次数，从而使所得IMF分量保留原始信号中幅值和频率的调制信息［5］。

当h1k满足SD的要求时，令c1=h1k，即可得到信号x（t）的第一个IMF分量，它代表了原始信号序列中的频率最高的组成成分。从原始数据序列x（t）中减去第一个IMF分量c1，就得到一个移除了高频组分的差值数据序列：r1=x（t）-c1。若r1中仍包含x（t）的较长周期的局部特征时间尺度信息，可将r1作为待分解信号，再重复式（1）—（3）的过程，直到所剩信号r1中的信息对所研究目的而言意义已很小或者已是单调函数时即可停止分解运算，此时的rn就代表着原始数据序列的趋势或均值。至此，便得到了信号x（t）的一系列IMF分量：c1，c2，…，cn，且r1-c2=r2，r2-c3=r3，…，rn-1-cn=rn。原始数据序列即可由这些IMF分量以及1个均值或趋势项表示：

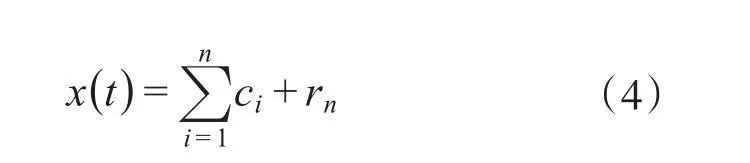
EEMD方法是在每次开始初始分解前，在原始信号序列中添加具有一定幅值的白噪声，然后再应用EMD方法进行分解，如此重复多次，直至分解完成，再取各IMF分量的各次分解值进行求和以得到最终分解结果。EEMD方法在继承EMD方法的自适应分解特征的同时，通过引入白噪声再进行集合平均，使得最终分解得到的IMF分量保持了物理意义上的唯一性。

2　结果

运用EEMD方法对图1所示的多伦气象站1956—2014年的年降水量序列进行多时间尺度分解，扰动白噪声与原始序列的信噪比取0.2，集合的样本数取100，分解结果如图2—6所示。

从中，可知以下结论：

（1）多伦站的年降水量序列可以分解为4个具有不同周期的波动分量和1个趋势分量，反映了区域气候系统变量变化所具有的复杂时域性。

（2）IMF1分量具有准2～4年波动周期，其波动幅度在近60年来没有明显的趋势变化。

（3）IMF2分量具有准4～6年波动周期，其波动幅度在20世纪90年代之后较20世纪50—80年代为小。

（4）IMF3分量具有准10年波动周期，其波动幅度在20世纪90年代之后较20世纪50—80年代为大。

（5）IMF4分量具有准15～20年波动周期，其波动幅度在近60年来呈增加趋势。

（6）Res分量显示的是年降水量的整体变化趋势，就整体而言，多伦站年降水量在近60年来呈衰减趋势，降幅为15.63％。值得指出的是，多伦站年降水量序列的变化趋势项可能属于更长周期（更小频率）波动的组成部分，而限于观测时限，Res分量的波动周期和振幅目前还难以准确测知，有待随着观测时限的延长逐步得以展现。

图2　多伦站年降水量序列的IMF1分量

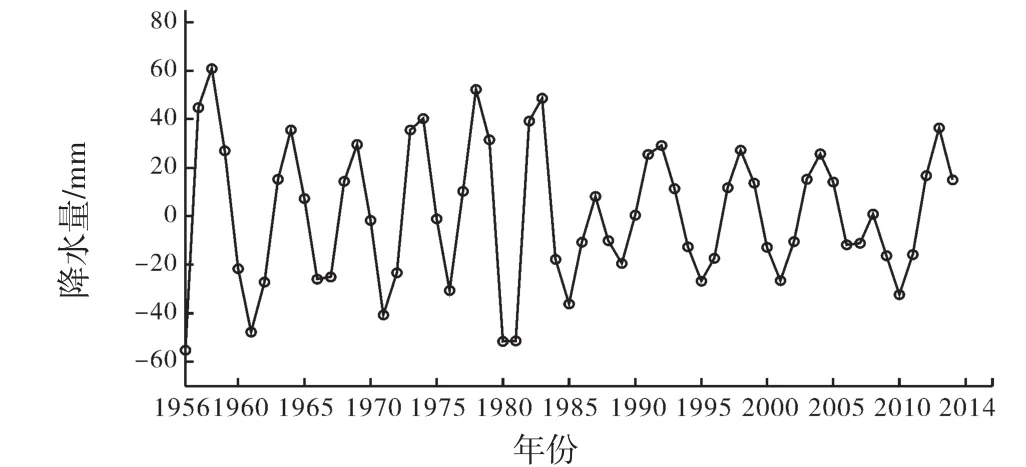
图3　多伦站年降水量序列的IMF2分量

图4　多伦站年降水量序列的IMF3分量

图5　多伦站年降水量序列的IMF4分量

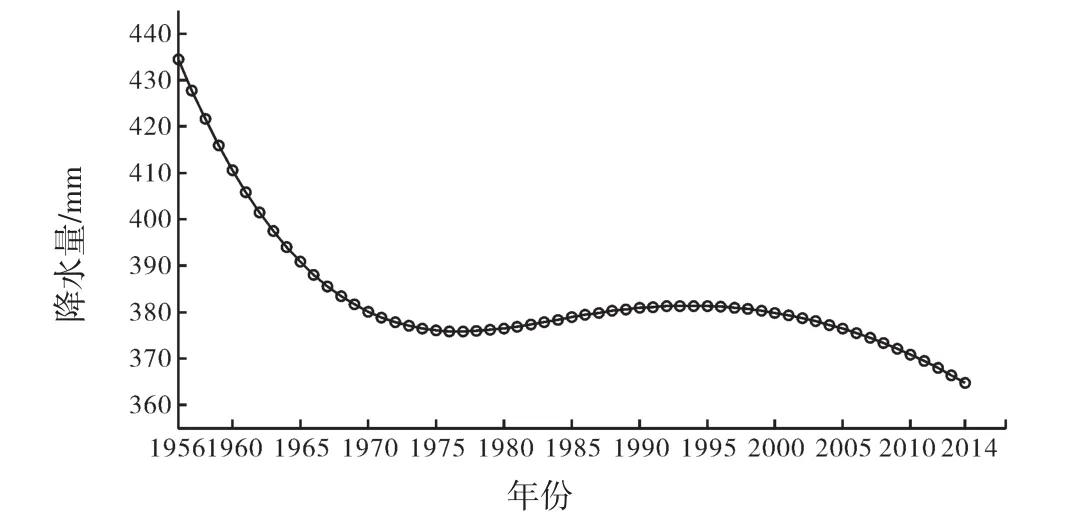
图6　多伦站年降水量序列的Res分量

3　结语

笔者以多伦气象站1956—2014年的年降水量序列为基础，运用EEMD分析了滦河上游流域年降水量的多时间尺度变化特性，揭示了其在不同时间尺度上所具有的不同周期和不同幅度的波动演化趋势，年降水量值变化在整体上呈衰减趋势。作为滦河的发源地和主要产流区之一，天然降水量衰减使得滦河上游流域产汇流系统的主要输入项量值受到较大影响，加之人类活动对下垫面状况的改变，使得河源区的地表与地下水资源量衰减更甚。在未来一段时期内，随着上游流域经济社会快速发展，工农业生产和居民生活需水量将呈增加趋势，流域水资源供需矛盾将逐渐突出。为此，需要切实加强节约用水工作、开展滦河上游冀蒙两省省际水量分配、认真贯彻落实最严格水资源管理制度，努力实现人水和谐的可持续发展。

［1］张少文，丁晶，廖杰，等.基于小波的黄河上游天然年径流变化特性分析［J］.四川大学学报（工程科学版），2004，36 （3）：32-37.

［2］Tewfiki A H.On the optimal choice of a wavelet for signal representation［J］.IEEE Trans Information Theory，1992，38 （2）：747-765.

［3］Norden E H，Shen Z，Long S R，et a1.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society A：Mathematical，Physical and Engineering Sciences，1998，454：899-955.

［4］WU Z，HUANG N E.Ensemble empirical mode decomposition：a noise-assisted data analysis method［J］.Proceedings of the Royal Society A：Mathematical，Physical and Engineering Sciences，1998，454：899-955.

［5］冯平，丁志宏，韩瑞光.基于EMD的洮河年径流量变化多时间尺度分析［J］.干旱区资源与环境，2008，22 （12）：73-76.

TV125

A

1004-7328（2016）04-0037-03

10.3969/j.issn.1004-7328.2016.04.012

2016—03—18

张小鹏（1979—），男，助教，主要从事水利水电工程教学与研究工作。