风险项目投资组合决策的一个均值-半绝对离差模型

郑媛媛,胡支军

(贵州大学 理学院，贵州 贵阳 550025)



风险项目投资组合决策的一个均值-半绝对离差模型

郑媛媛,胡支军*

(贵州大学 理学院，贵州 贵阳 550025)

项目投资组合选择是许多风险投资机构的重要决策问题。现有的研究大多集中于探讨在各种准则下如何识别“正确”的项目组合，例如收益和风险准则。在下半绝对离差风险度量基础上，采用Bayes方法对项目未来收益的事前估计值进行修正，建立了均值-半绝对离差项目投资组合优化模型，并利用Monte Carlo模拟方法将模型转化为混合整数规划问题。理论和模拟分析表明，对估计不确定性的显式Bayesian建模，并使用所获得的项目收益修正值进行投资组合选择比直接基于项目的事前价值估计的投资组合选择获得的期望效用高，并且前者能够消除投资组合的事后实现效用值与事前估计效用值之间的预期间隔，从而降低投资家可能经历的事后失望程度。

风险投资组合；风险厌恶；Bayesian方法；决策分析

在市场竞争日渐激烈的经济背景下，风险投资组合越来越成为理论和实践关注的热点问题。风险投资是指风险投资家为获得高收益而将资金投入到有较大风险的高新技术开发项目的一种投资行为。它具有高收益、高风险的特点。投资家通常为了有效规避投资风险的同时提高投资回报率，会把资金分别投入到不同的多个项目，即进行组合投资。因此，合理地衡量投资风险，进而科学地做出风险投资组合决策对投资家来说至关重要。

现阶段，关于风险投资组合的理论主要集中于事中决策研究，它们给出的大多是在项目实施过程中的决策，这与决策者需要在事前给出最优决策的事实不符。现有的对于事前决策的项目投资组合理论研究相对较少，它们主要是在Markowitz(1952)[1]提出的均值-方差投资组合模型的基础上发展而来。例如，Yiu等(2010)[2]考虑了当风险资产的价格波动服从马氏几何布朗运动时基于最大风险值的最优投资组合选择问题。Huang等(2010)[3]研究了如何在仅知道证券投资组合收益率的潜在概率分布服从一个特定集合的情况下，用稳健的CVaR方法选择投资组合。张卫国等(2013)[4]把可能性理论和可信性理论应用到风险投资组合的决策当中，分别建立了基于可能性理论的风险投资组合决策模型和基于可信性理论的风险投资组合决策模型。崔雪婷(2013)[5]基于不同风险度量以及实际交易特征进行投资组合选择,以缩小投资组合理论模型和实际应用之间的差距。Hall等(2015)[6]讨论了当具有每个项目的不确定收益的部分概率分布信息时的项目选择问题，决策者选择备选项目组合的一个可行子集使得投资组合收益不能达到某个给定目标的风险最小化。

一般地，风险项目的价值由于受某些不确定的未来事件的影响而具有不确定性。对此，风险投资家在实际投资过程中会充分利用关于项目价值的先验信息来对项目未来的实现价值进行预测。或者根据这些先验信息进一步获得项目价值的后验估计值，然后再基于项目价值的估计值做出投资决策，以此来降低不确定性并改进决策过程。然而，项目价值的估计值通常也存在不确定性，这使得对项目未来价值的预测不可避免地存在随机误差。并且即使项目的事前价值估计是无偏的，也可能会存在一部分价值较小的项目因为被过高的估计而被投资家选择。这将导致投资家选择的风险投资组合的事后实现价值低于事前估计值，使其产生决策后的失望。

Vilkkumaa等(2014)[7]提出对风险项目价值估计的不确定性进行Bayesian建模，并将所获得的Bayes修正估计值作为风险投资组合的决策依据。进一步，他们证明了和直接基于项目价值的事前估计值选择的投资组合相比，基于Bayes修正估计值选择的风险投资组合实现的事后价值更多，投资家经历的决策后失望程度较低，并且它能够消除风险投资组合事后实现价值与事前估计价值之间的间隔。然而，文献[7]的研究没有考虑决策者对风险的态度，认为决策者是风险中性的。

事实上，在现实交易中决策者面对具有相同收益的项目会倾向于选择风险较低的项目,即表现出风险厌恶的心理偏好。为了使模型更加符合实际情况，我们需要在风险投资组合决策的研究中考虑决策者风险厌恶的心理偏好，这就使得对于如何准确地选择风险度量指标在理论研究中显得尤为重要[8]。Markowitz(1952)[1]提出用方差描述投资风险，Kono等[9,10]又提出用收益率的绝对离差表示风险。这两种风险度量方法赋予以均值计算的正负离差相同的权重，不能满足决策者对风险的真实心理。为了克服方差计量风险的不足，人们提出了把小于目标收益的收益作为风险计算因子的下方风险计量。下方风险默认投资家对超过目标收益率时是风险中性的，无法反映投资家对更好的投资机会的追逐。

对于具有标准化概率分布(原概率分布减去均值)的风险方案，由于均值为零，决策者对它们的偏好和风险的评价具有相反的一致性。根据这样一个认识,Jia等(1996)[11]提出了基于负期望效用的标准风险度量理论和模型，这一模型的发展为风险与偏好建立了一个完整的关系，并对各种风险模型的评价提供了共同的效用理论基础。以往的许多风险模型(如方差、半方差等)都是标准风险度量模型的特例。

基于Vilkkumaa等(2014)[7]的研究，本文将投资家的风险厌恶心理融入风险投资组合优化模型中，用下半绝对离差度量风险，采用Bayes方法对项目未来收益的事前估计值进行修正，以此建立均值-半绝对离差的风险厌恶投资组合优化模型。其中，项目的事后可能实现价值和事前估计价值是由Monte Carlo方法随机模拟产生。研究发现，对估计不确定性的显式Bayesian建模并使用所获得的修正估计进行投资组合选择比直接基于事前价值估计的投资组合选择获得的期望效用高，并且前者能够消除投资组合的事后实现效用值与事前估计效用值之间的预期间隔，从而降低投资家可能经历的事后失望程度。

1　不确定环境下的风险投资组合选择

如何衡量投资组合的风险是风险投资决策一个关键问题。一般地，在被投资前，项目的最终实现值是未知的，只有当项目被执行后才能实现，进而被观测。但是项目最终收益服从的分布已知，这给风险投资家做出风险投资决策提供了重要的依据。

设X为项目投资组合的收益，μ为X的期望值，则X′=X-μ是一个零期望值的标准风险变量,Jia等(1996)[11]提出了如下标准风险度量模型

(1)

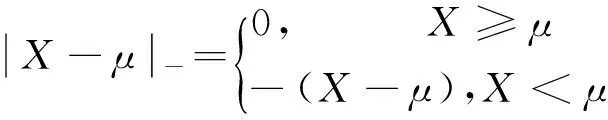
模型(1)中，R(X′)为投资组合所面临的投资风险，d反映了当投资组合的收益低于期望收益时投资家的失望程度，e表示当投资组合的收益高于期望收益时投资家的开心程度。通常人们对失望的反应比对开心的反应更加强烈，所以有d>e。

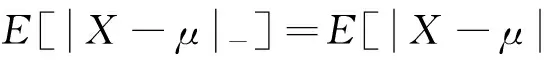
(2)

其中，λ=d-e>0为风险厌恶系数，反映了风险对于财富效用的重要程度，它衡量了财富效用和风险之间的关系。根据(2)式，风险投资家的效用函数由两部分组成：一部分是风险投资组合最终实现的期望收益，一部分是由风险投资家的风险厌恶带来的效用损失。

现假设存在N个风险项目供投资家选择，它们获得融资后产生的价值为：v=[v1,…,vN]T，项目的价值描述了投资家在期末可以从项目投资中获得的收益。这些项目的价值为随机变量V=[V1,…,VN]T～f(v)的实现值，其联合密度函数f(v)是已知的。

在考虑项目投资预算或其他约束的条件下，风险投资家本着最大化期望效用的原则从这些备选项目集合中选择一个子项目集。用一个具有二元值的决策变量z=[z1,…,zN]表示风险投资家选择的投资组合，当且仅当项目i被选择时，令zi=1，否则令zi=0。用Z表示满足相关约束条件的可行投资组合。如果风险投资家知道了项目价值v，则他将通过求解下面的优化问题确定最优投资组合

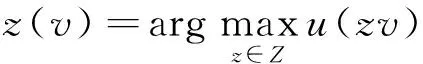
(3)

其中u(·)为由(2)式定义的风险投资家的效用函数。

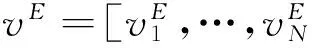
(4)

利用Matlab软件，由Vi～N(8,32)生成项目P1,…,P10的价值的一组实现值vi分别为：9.60，13.50，1.22，10.59，8.96，4.08，6.70，9.03，18.74，16.31。根据模型(3)，令风险厌恶测度λ=0.6，则求得最优投资组合z(v)由项目{P1,P2,P4,P9,P10}组成。此时，实现的项目总效用值u(z(v)v)为68.74。

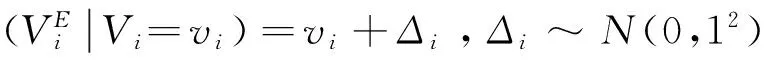
从这个例子可以发现：(ⅰ)基于估计值vE的投资组合z(vE)所实现的事后项目总效用值(63.22)低于最优投资组合z(v)所实现的总效用值(68.74)；(ⅱ)投资组合z(vE)包含了“激进型”项目P6，这个项目由于具有较高的估计值(11.74)而被选取，但它们没有被最优投资组合z(v)选取，因为它的实际值只有4.08；(ⅲ)投资组合z(vE)的事前总估计值(76.27)比其实际所实现的事后总价值(63.22)高20.64%,表明决策者会经历决策后的失望。

对以上结果进行分析，本文得到下面的定理1。

定理1设VE是V的一个条件无偏估计，则

E[u(z(VE)V)-u(z(VE)VE)]≤0

其中，z(V)和z(VE)分别是问题(3)和问题(4)的最优解。进一步，若P(z(V)≠z(VE))>0，则E[u(z(VE)V)-u(z(VE)VE)]<0。

证明对于给定的v和vE，由(3)式和(4)式得

u(z(vE)v)-u(z(vE)vE)

≤u(z(v)v)-u(z(vE)vE)

≤u(z(v)v)-u(z(v)vE)

(5)

=u(z(v)v)-u(z(v)v)=0

(6)

若选择非最优项目组合的概率为正，即P(z(V)≠z(VE))>0，则(5)式的第一个不等式对某些v和vE严格成立，进而对于相应的v，不等式(6)也严格成立。

定理1表明，在平均的意义下，投资组合z(vE)所实现的项目总效用值不会超过事先估计的总效用值。这样，若选择“错误的”项目的概率大于零，则项目组合实际所实现的效用值将严格小于事先估计的效用值。特别地，即使估计是无偏的，投资组合的效用值也可能会被系统地高估，使得风险投资家将经历决策后的失望。对项目真实价值的估计的不确定性越高，预期的失望也就更大。换言之，估计值的不确定性越高，不仅让识别真正具有最高价值的项目更难，而且使得选择被高估了的项目的概率更高。

2　风险投资组合中不确定性的Bayesian建模

(7)

特别地，若项目真实价值和估计值的分布是共轭分布，则可以获得Bayes估计的一个封闭形式的表达式[7,13]。例如，当项目的价值和估计值服从自共轭正态分布，即

项目的估计值：

则通过(7)式推导可以得到，对于每个项目有

(8)

依据项目期末价值的Bayes估计值对项目进行投资组合选择，可以缓解投资家决策后的失望[7,13]。据此，将Bayes估计下的最优投资组合定义如下

(9)

由模型(9)得到的基于项目的Bayes估计值选择的最优投资组合z(vB)的事后实现效用与事先估计效用的差距为u(z(vB)V)-u(z(vB)vB)。另外，为了研究模型(9)的平均表现，本文用随机变量VE代替(7)式中的vE，可得

(10)

本文指出，在相当一般的假设下，基于Bayes估计vB选择的投资组合所实现的期望效用值不会比基于估计值vE的投资组合所实现的期望效用值少。这一说法可以由定理2来解释。

定理2设V，VE及z(vE)的含义如定理1所示，z(VB)和VB分别由(9)式和(10)式给出，则

E[u(z(VE)V)-u(z(VB)V)]≤0

进一步，若P(z(VE)≠z(VB))>0，

则有E[u(z(vE)V)-u(z(vB)V)]<0

且E[u(z(VE)V)-u(z(VB)V)]<0。

证明对于给定的vE，则项目的Bayes估计vB、模型(4)和模型(9)的最优解z(vE)和z(vB)都是固定的。利用(7)式，求得u(z(VE)V)-u(z(VB)V)的条件期望为:

=u(z(vE)vB)-u(z(vB)vB)≤0

(11)

因此，对某些vE，若P(z(VE)≠z(VB))>0，则u(z(vE)vB)-u(z(vB)vB)<0。进一步，由(11)式可知，E[u(z(VE)V)-u(z(VB)V)]<0也成立。

定理2说明，在同样的假设条件下，基于项目Bayes估计值vB得到的最优投资组合的事后实现效用不会低于直接基于项目估计值vE得到的最优投资组合的事后实现效用。并且，如果使用Bayes修正值vB选择的投资组合与直接使用价值估计vE选择的投资组合不相同的概率非零，则基于Bayes修正值的投资组合z(vB)将会获得严格更高的效用。

定理3设V，VE，VB及z(·)的含义如定理2所示，则

对所有的vE成立，而且有E[u(z(VB)V)-u(z(VB)VB)]=0。

证明对给定的一组估计值vE，相应的Bayes估计值vB和问题(9)的最优解z(vB)也是固定的。对u(z(vB)V)-u(z(vB)vB)求条件期望可得

3　基于风险厌恶的风险投资组合优化模型

实际生活中，风险投资家在做投资决策前会对相关风险项目进行调查分析，然后选出符合投资标准的风险项目N个。但是由于总的投资预算有限，他只能从N个备选项目中选择n个项目进行投资。假设投资于风险项目i获得的价值为Vi，则考虑投资家风险厌恶心理的投资组合优化模型为

(12)

其中，若投资家投资第i个项目，则zi=1，否则zi=0。

由于线性优化模型(12)的目标函数是关于随机向量V的函数的数学期望，难以获得解析表达式，所以本文采用Monte Carlo模拟方法将问题(12)近似为确定性优化问题。

(13)

(14)

此外，为了考察风险投资家的风险厌恶行为对投资组合决策的影响，我们还求解如下的最大化项目组合总期望价值的投资组合优化模型[7]

(15)

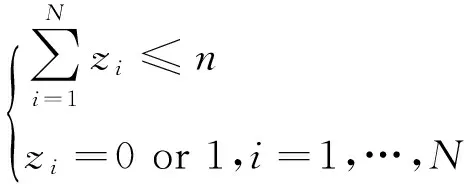
综上，模型(14)中的目标函数不仅反映了投资组合的期望效用值，还反映当投资组合的期末收益低于预期目标时风险投资家产生的风险厌恶心理对其效用的影响。而模型(15)则假设风险投资家是风险中性的，没有考虑投资家的风险厌恶心理。因此，模型(15)可以看作是模型(14)在风险厌恶测度λ=0时的一个特殊情况。

4　数值算例

4.1风险厌恶对投资组合选择的影响分析

为了检验风险厌恶的投资组合优化模型(14)以及对不确定性的Bayes建模在实际应用中的有效性，本文应用Monte Carlo方法随机模拟产生备选项目的价值数据，并分别计算模型(14)和模型(15)的最优投资组合方案。

设定如下情形：某风险投资机构有12个风险项目P1,…,P12可供选择[7]，且由于资金有限，它只能从12个备选项目中选取5个项目进行投资。这些备选项目的期末价值vi是独立同分布的随机变量Vi=μi+Ei的实现值。其中，前6个项目(P1至P6)经营的是传统的项目，投资家对它们未来的业绩的估计相对精确，其估计误差相对较小，假设Δi=1；后6个项目(P7至P12)是风险较高的新颖“激进型”项目，投资家对它们未来的业绩的估计相对粗略，其估计误差相对较大，假设Δi=5。

表1　风险厌恶行为对风险投资组合选择的影响

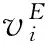
4.2项目估计的不确定性对投资组合选择的影响分析

为了分析项目价值估计的不确定性对决策后的失望程度的影响，本文将借助Matlab软件进行数值案例分析。

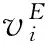
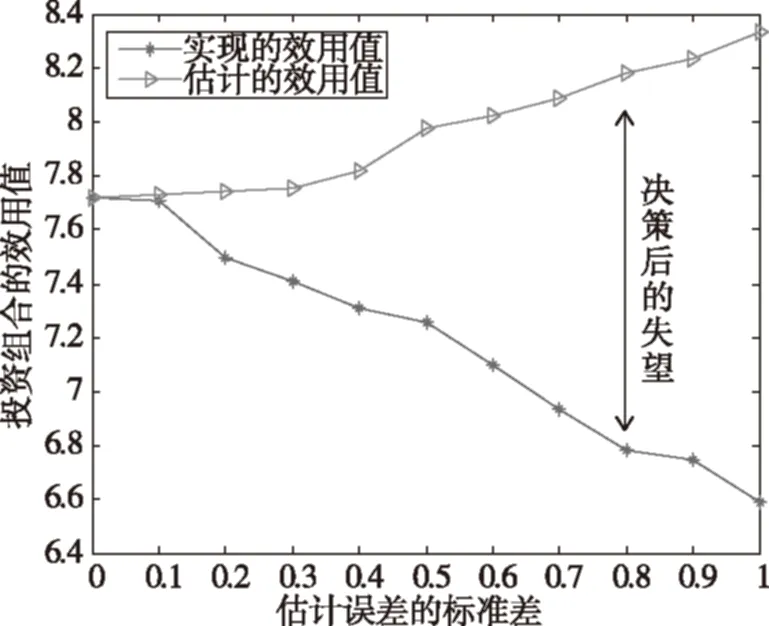
图1　直接基于项目价值的事前估计值选择的投资组合的平均效用估计值与平均效用实现值

图2　基于Bayes修正估计值选择的投资组合的平均效用估计值与平均效用实现值

分别地，图1给出了当估计误差的标准差增大时，基于项目的直接估计价值VE求解模型(14)获得的投资组合的估计平均效用值和事后实现平均效用值的变化情况。可以看出，随着项目价值的估计误差标准差τ的增大，决策后的失望程度也增大。例如，在图1中，当τ=0.8时，所选择的投资组合估计的平均效用值为8.18，比其所实现的平均效用值6.78高20.65%。这说明，随着项目价值估计不确定性的增大，决策者识别真正高价值项目的难度也增大，其面临的决策失望也同样增大。这一结果印证了定理1的结论。

图2给出了当估计误差的标准差增大时，利用Bayes估计值求解模型(14)获得的投资组合的估计平均效用值及其事后实现平均效用值的变化情况。可以看出，对项目价值的估计值进行Bayes修正后再进行投资组合决策，可以减轻决策者的事后失望程度，这个结果也与定理3的结论相印证。

5　结论

目前，关于风险投资组合的研究主要是事中决策研究，这与决策者需要在投资前做出投资决策的事实不相符。基于此，本文考虑投资家的风险厌恶心理，用下半绝对离差度量投资家的投资风险，并对风险项目价值估计的不确定性进行Bayesian建模并获得其Bayes修正值，进而建立均值-半绝对离差的投资组合优化模型。利用Monte Carlo随机模拟方法，对基于风险厌恶的投资组合优化模型与基于风险中性的投资组合优化模型进行对比分析，发现投资家的风险厌恶心理对其投资决策具有重要的影响。此外，理论分析与模拟结果表明，基于项目价值的Bayes修正估计选择的投资组合比直接基于项目价值的事前估计选择的投资组合获得的期望效用高，且前者能够消除投资组合的事后实现效用值与事前估计效用值之间的预期间隔，从而降低投资家可能经历的事后失望程度。

[1] Markowitz H. Portfolio selection[J]. Journal of Finance, 1952, 7(3): 77-91.

[2] Yiu K C, Liu J Z, Siu T K, et al. Optimal portfolios with regime switching and value-at-risk constraint[J]. Automatica, 2010, 46(6): 979-989.

[3] Huang D S, Zhu S S, Fabozzi F J, et al. Portfolio selection under distributional uncertainty: a relative robust CVaR approach[J]. The European Journal of Operational Research, 2010, 203: 185-194.

[4] 张卫国,梅琴,陈炽文.具有模糊收益的项目投资组合优化方法[J].管理学报,2011,8(6):938-942.

[5] 崔雪婷. 基于不同风险度量和交易约束的投资组合选择问题研究[D].上海：复旦大学,2013.

[6] Hall N G, Long Z Y, Qi J, et al. Managing underperformance risk in project portfolio selection[J].Operations Research, 2015, 63(3):761-770.

[7] Vilkkumaa E, Liesiö J, Salo A. Optimal strategies for selecting project portfolios using uncertain value estimates [J]. European Journal of Operational Research, 2014, 233(3): 772-783.

[8] 黄秀路.基于CVaR风险度量角度的投资组合优化模型的理论与实证研究[D].成都：西南财经大学,2013.

[9] H Konno, H Yamazaki. Mean-absolute deviation portfolio optimization model and its application to Tokyo stock market[J]. Management Science, 1991, 37(5): 519-531.

[10]H Konno, T Koshizuka. Mean-absolute deviation model[J]. IIE Transcations, 2005(10): 893-900.

[11] Jia J, Dyer JS. A standard measure of risk and risk-value models[J]. Management Science, 1996, 42(12): 1691-1705.

[12] Jia J, Dyer JS，Butler JC. Generalized disappointment models[J]. Journal of Risk and Uncertainty, 2001, 22(1):59-78.

[13] Smith J E, Winkler R L. The Optimizer’s Curse: Skepticism and Postdecision Surprise in Decision Analysis[J]. Management Science, 2006, 52(3): 311-322.

(责任编辑：周晓南)

A Mean-semi-Absolute Deviation Model for Venture Project Portfolio Decision

ZHENG Yuanyuan, HU Zhijun*

(College of Science，Guizhou University，Guiyang 550025，China)

Project portfolio selection is an important decision in many organizations. Most studies on project portfolio selection focus on identifying the ‘right’ project portfolio under various criteria, such as reward and risk. Based on lower semi-absolute deviation risk measurement, and Bayesian methods was used to revise the value of ex ante estimates about the future values of alternative projects, a portfolio optimization model of mean-lower semi-absolute deviation was constructed. Further, the model was transformed into a linear programming problem by the Monte Carlo simulation method. The analysis of theory and simulation shows that the explicit Bayesian modeling of estimation uncertainties and the use of resulting revised estimates in portfolio selection has a higher expected utility value in comparison with the straightforward portfolio selection based on ex ante value estimates, and the former can eliminate the expected gap between the realized ex post portfolio utility value and the estimated ex ante portfolio utility value, to reduce the amount of ex post disappointment that the venture capitalist may experience.

venture capital portfolio; risk aversion; Bayesian methods; decision analysis

1000-5269(2016)02-0134-07

10.15958/j.cnki.gdxbzrb.2016.02.29

2015-12-08

国家自然科学基金资助项目(71361003，71271090)；贵州省自然科学基金项目([2011]2102)；贵州省教育厅人文社科规划项目(13S5D005)

郑媛媛(1989-)，女，硕士研究生，研究方向：金融优化、决策分析等，Email：15285118897@qq.com.

胡支军，Email：zjunhu75@163.com.

F830;O221

A