低质量相接双星的研究进展
宋 芬
(1.集美大学 理学院,福建 厦门 361000;2.中国科学院天体结构与演化重点实验室,云南 昆明 650011)
低质量相接双星的研究进展
宋芬1,2*
(1.集美大学 理学院,福建 厦门 361000;2.中国科学院天体结构与演化重点实验室,云南 昆明 650011)
密近双星的观测和理论研究是恒星物理研究中热点之一。解释低质量相接双星的观测是双星演化的难点。本文通过对低质量的相接双星的实测资料(光变曲线和物理参量)和理论模型进行综述,提出了该类双星研究中主要存在的问题,这对于丰富和完善双星演化理论具有重要意义。
双星;相接双星;双星演化
密近双星中子星的演化受另一颗子星的影响,甚至两子星间发生复杂的物理过程,其演化过程与单个恒星演化的结果明显不同。为此,密近双星是恒星演化研究中一类特殊而又重要的对象,在很长一段时间内引起了天体物理学家的兴趣。
依据密近双星两子星是否充满其各自的洛希瓣临界体积,从几何上将密近双星分为三类[1]:一类是分离双星,两子星均未充满各自的洛希瓣临界体积;第二类是半分离双星,其中一颗子星充满其相应的洛希瓣临界体积,两子星之间发生物质交换过程;第三类是相接双星,两子星均充满各自的洛希瓣临界体积并形成公共包层,伴随物质交换等复杂的物理过程,是密近双星中较特殊的系统。两子星质量较小且具有公共对流包层的相接双星系统,又称W UMa型相接双星或低质量相接双星,其光变曲线表现为主极小与次极小食深几乎相等的EW型,质量不同的两子星表面有效温度近似相等。本文主要讨论具有公共对流包层的低质量相接双星。
观测上,采用分光和测光技术,获得相接双星观测样本的精确物理参量。具有精确物理参量的低质量相接双星的数据较多,且不断增加。从光变曲线方面,观测发现该类系统存在O’Connell 佯谬和Binnendijk 佯谬[2]等现象;从质量、光度和半径等物理参量上,分析出其存在Kuiper佯谬[3]和周期-颜色关系带[4]等规律。为解释该类系统的观测现象,理论上提出了多种模型。由最初的热平衡模型,发展至今的非热平衡模型。目前,非热平衡模型中以Robertson & Eggleton“热弛豫震荡模型”[5]、“Kähler 模型[6]”、“Stepień模型[7]”为代表,尝试从理论上诠释低质量相接双星的观测现象。事实证明,理论模型已经能够解释低质量相接双星的周期-颜色关系和Kuiper佯谬。模型中物理过程的处理和假设,直接决定了理论计算的结果,摸索清楚物理过程是解决问题的关键。
本文基于低质量相接双星的观测事实,重点介绍现今主要的几类相接双星非热平衡理论模型,及其能够解释的观测现象,并总结目前相接双星理论模型的研究现状,分析讨论其存在的问题。
1 低质量相接双星观测事实
从低质量相接双星的质量、半径等物理参量出发,Kuiper[3]统计发现位于主序演化带附近的该类系统所满足的质量-半径关系与理论演化预言出的质量-半径关系R≈M0.6-1.0不符,出现了观测事实与理论结果相悖逆的现象(即‘Kuiper 佯谬’);Kähler[4]在Eggen 1967基础上拟合出该类样本在周期-有效温度关系图中呈带状分布(两边界线分别为1.5logTeff-logP=5.975与1.5logTeff-logP=6.15), Gazeas & Stepień 2008[8]结合该类系统绝对星等与周期和颜色的关系,提出周期-绝对星等关系为MV=-8.4logP+0.31,同时统计提出较大质量子星满足的质量-半径关系和周期-质量关系以及较小质量子星的周期-质量关系规律分别为:

logM1=(0.755±0.059)logP+(0.416±0.024),
logM2=(0.352±0.166)logP-(0.262±0.067)。
其中:M1,R1,M2分别表示较大质量子星的质量和半径以及较小质量子星的质量。Gazeas & Stepień还发现较大质量子星的质量-半径关系满足理论主序恒星的质量-半径关系,而较小质量子星的质量-半径关系没有明显规律(同Kuiper[3]观点)。从理论模型演化上计算,Gazeas & Stepień给出低质量相接双星演化发生并合,成为单个快速旋转的恒星的可能性。除此之外,Csizmadia & Klagyivik 2004[9]研究发现该类系统在质量比-光度比关系图上规律地分布于关系线(Lucy 1968a[10])
附近,没有准确的质量比-光度比关系,同时证明相接阶段能量转移与质量比和光度比有关。
从低质量相接双星光变曲线上,发现不同质量的子星有近似相等的表面有效温度,将这类现象称为‘Lucy 佯谬’;在不发生掩食时系统总亮度不等,这类现象称为“O’connell 效应”。
在光变曲线研究过程中,天文学家根据低质量相接双星的光变曲线主极小对应被掩食子星的不同,将该类系统再次细分为A次型低质量相接双星和W次型低质量相接双星进行讨论。若主极小对应被掩食的子星为较大质量子星,表明较大质量子星的有效温度较较小质量子星的有效温度高,称这些样本为A次型低质量相接双星;若主极小对应被掩食的是较小质量的子星,这表明质量较小的子星有效温度稍大于质量较大的子星,称为W次型低质量相接双星。W次型系统中出现的质量较小的子星表面有效温度稍大于质量较大的伴星这一现象,称为‘Binnendijk 佯谬’[2]。对于A次型与W次型两类系统间的演化联系,Maceroni,et al[11]提出两类系统的分类与系统所处的演化阶段和起源无关,两者之间无演化联系,同时Yildiz & Dogan 2013[12]通过推算出A次型与W次型子星的初始演化质量不同,也证实了该想法。
2 理论模型研究进展
Kuiper 1941[3]提出两子星质量不等的低质量相接双星系统具有公共包层,两子星表面处于等势。Lucy 1968[10]假设Kuiper 结论的正确性,建立了热平衡模型,假设相接双星中较大质量子星将一部分能量转移给较小质量子星,使得两子星表面处于等势。该模型成功地诠释了该类系统的光变曲线现象[10]。直至Rucinski 1973[13],1974[14]指出W次型W UMa型系统表面不处于热平衡状态,发现热平衡模型的不正确性。Lucy 1976[15]与Flannery 1976[16]分别提出了低质量相接双星的非热平衡模型,成功地解释了低质量相接双星的周期-颜色关系。继Lucy和Flannery之后,许多不同的非热平衡模型被提出(如Robertson & Eggleton 1977[17], Kähler 1986a[18],1986[19],Stepień 2006[7]等模型),发展至今,理论演化模型正在不断完善。
双星理论演化模型不仅要计算半分离阶段的物质交换,还要考虑相接阶段的能量交换和物质交换物理过程,同时计算由于不同物理机制引起的星风物质损失(如磁制效应) 和角动量损失。Eggleton 2010[20]提出总质量在1至3 M⊙范围内且周期小于4天的密近双星的理论演化计算,给出核演化、洛希瓣物质交流、恒星星风物质损失(快速转动加剧星风损失)、潮汐摩擦、轨道角动量损失(包含由恒星星风、磁制效应和潮汐摩擦物理机制引起的损失)、相接阶段的物质转移和能量转移这七大物理过程是理论模型中的基本过程,发现由不同物理机制引起的星风物质损失和角动量损失(非守恒效应),对双星的早期演化产生影响,甚至对演化后期形成的低质量短周期相接双星有重要作用。除该工作外,以下四个模型均用于诠释低质量相接双星,其中Kähler 1986[19]模型为守恒演化计算,其它为非守恒演化。
2.1热弛豫震荡模型
热弛豫震荡模型(TRO model)计算出了双星系统在相接阶段和半分离阶段之间的循环演化[17]。相接阶段,较大质量子星转移能量给较小质量子星(能量交换的量由观测规律即两子星表面半径和质量满足的关系与两子星表面有效温度近似相等给出的,为公式(1))[17],较小质量子星获得能量后膨胀,并将自身质量转移给较大质量子星,经过一段时间的演化后,较小质量子星退回洛希瓣内,系统进入半分离阶段。在半分离阶段,较大质量子星继续充满其洛希瓣,将物质转移给较小质量子星,待较小质量子星获得足够物质后再次膨胀充满其洛希瓣,系统再次回到相接,演化结果如图1。
(1)
其中:M1,M2,L1,L2分别表示子星1和子星2的质量和光度,f表示能量转移的有效系数,为可调参量。
图1中两循环演化实线分别经历了A、B、C、D、E等阶段,左下角循环演化实线ABCDE表示较小质量子星的演化,右上角循环演化实线ABCDE表示较大质量子星的演化。A点表征半分离阶段开始,较大质量子星转移质量给较小质量子星,较小质量子星演化至B点时膨胀充满其洛希瓣,系统进入相接,物质转移方向被反转,发生物质和能量交换。系统演化至C点又再次进入半分离阶段,如此循环演化震荡,演化的最终产物可能发生并合。

图1 TRO模型的质量-半径演化图[17]
Li,et al[21-23]在Robertson & Eggleton 1977[17]的基础上,进一步讨论相接阶段的物理过程。模型假设如下:i)两子星为球形;ii)两子星同步转动,其公转运动轨道为圆形;iii)考虑了两子星的自转对恒星结构和演化的影响,但忽略公转对系统演化的影响;iv)角动量计算中包含了轨道角动量和自转角动量,计算由磁星风引起的角动量损失; v)相接阶段,物质交换与能量交换过程是分开并独立的。
在该模型中,两子星随时间演化逐渐膨胀,较大质量的子星膨胀并充满其洛希瓣体积,系统进入半分离阶段,发生物质交换过程,较大质量子星转移物质给较小质量子星,较小质量子星(质量较小子星)获得质量后膨胀充满其洛希瓣体积,系统进入相接阶段(R1>Rcrit1且R2>Rcrit2,其中Rcrit1和Rcrit2表示两子星的洛希瓣临界半径),发生物质交换和能量交换,其中能量交换与物质交换是两个相互独立并分开发生的过程。为了使得相接阶段系统两子星表面处于等势,Li,et al[21]计算出对应不同质量比、不同相接度的等势半径网格,确保在物质交换后两子星仍处于等势状态,相接阶段物质交换速率公式改进为:

相接阶段,较小质量子星获得能量后,转移质量给较大质量子星。能量交换的量引自Robertson & Eggleton 1977[17],其能量交换经验公式[21]为:
ΔL=fΔL0

由以上物理过程组成的相接双星模型,其预言出的以热时标进行的热弛豫震荡演化结果成功地诠释了低质量相接双星的周期-颜色关系,结果如图2。图中两平行实线表示观测统计出的周期—颜色关系,循环绕圈实线表示理论演化计算出的周期—颜色关系,理论演化正在逐渐进入观测规律带。

图2 Li,et al模型的周期-颜色关系图[23]
图2相接双星中较大质量子星演化的周期-颜色关系与观测统计的周期-颜色关系的比较,理论结果与观测吻合。
2.2Kähler模型
Kähler 2002[6]提出了相接双星的简单模型,对相接双星的结构方程重新进行讨论,给出两子星之间的物质交换公式,分析能量交换的不确定性,试图解决相接双星理论与观测的矛盾。模型中假设两子星为球形并同步转动,双星总质量和总角动量守恒,两子星均处于流体静力学平衡。双星演化模型中的边界条件由两子星随着时间演化的表面平均势能决定。两子星表面平均势能的计算公式(Kähler 1986[19]):

当两子星的势能ψi均小于ψL1时,双星系统处于分离状态;当两子星中任意一颗子星表面平均势能大于ψL1,则系统处于半分离状态,较大质量子星转移物质给较小质量子星;当两子星表面平均势能均大于ψL1时,系统进入相接阶段,发生着物质交换和能量交换。ψL1表示拉格朗日点L1处的洛希势能。
物质交换速率由声速、密度和系统颈部的有效区域来决定,计算公式为式(2)[6]。该物质交换速率公式根据双星系统整个演化过程中结构的变化定量给出系统发生物质交换的量。半分离阶段Bg=0,物质交换计算公式为式(2)。相接阶段当Bg< (2) Kähler将该模型应用于低质量相接双星时,假设能量交换发生在两子星的壳层,其能量转移包含两部分,一部分为相接阶段较小质量子星转移物质时,随着转移的物质被较大质量子星获得时所吸积的光度,另一部分为通过公共包层较大质量子星转移给较小质量子星的能量[6]。 (3) 其中:Λ表示能量交换的量,fE为小于1的可调参数,ρ1、ρ2、P1和P2分别表示两子星的内临界洛希面上的密度和压强,s1-s2为两子星表面熵差。 该模型中同样假设相接阶段的物质交换与能量交换过程是分开并且独立,认为进入相接阶段的半分离双星,由较大质量的子星转移物质给较小质量的子星,较小质量的子星得到质量后膨胀再转移能量给较大质量子星。基于这些思想,模型的演化时标为热时标,系统处于半分离和相接阶段来回震荡的热弛豫震荡演化结果。Li,et al[21-23]和Kähler[24]成功地解释了低质量相接双星观测中的周期-颜色关系(图3)。图中两平行虚线表示观测统计的周期—颜色关系范围,位于该观测带范围内的黑粗线为模型计算出的理论结果。 图3 Kähler模型的周期-颜色关系图[24] 2.3HSB模型 HSB模型[25]考虑星风物质损失造成系统质量丢失和角动量损失,分析子星在自转离心力、公转离心力和潮汐力作用下双星的演化,子星的结构由球形结构偏离为非球形,两子星的内部结构和物理过程发生变化,导致子星内部发生化学元素的迁移,对相接双星的演化带来重要影响。模型中假设相接阶段的物质交换过程和能量交换过程是同时进行且相互联系的,能量交换量由发生转移的物质自身携带的热能ΔET、动能ΔEK和势能ΔEP所组成[25]。 ΔE=ΔEP+ΔEK+ΔET (4) 采用以上处理,模型给出了双星系统从分离阶段开始演化,经历半相接至相接阶段,随后又进入半相接阶段,直至两子星可能发生并合的双星演化结果。Song & Huang 2012[26]收集了具有精确物理参量的低质量相接双星,应用该模型解释观测数据在质量-光度、质量-半径和赫罗图上呈现出的演化规律,发现模型能够很好地吻合这些规律。 2.4Stepień模型 Stepień 2006[7]假设低质量相接双星是经过case A或case B演化时两子星达到质量反转后形成的(case A为物质交换过程发生于主星中心氢燃烧阶段,case B为物质交换过程发生于主星氢壳层燃烧阶段),其次星处于主序阶段,主星是经过主序演化后进入主序后的恒星,该模型成功地解释了观测统计出的质量-半径关系(结果如图4[7]),即Kuiper佯谬。 该模型的主要思想如下:首先,分离双星系统在主序阶段的演化中计算由磁星风造成的轨道角动量损失,其轨道角动量的计算公式[7]为 (5) 又根据类太阳转动恒星的星风损失观测数据,推导出冷密近双星轨道周期变化的半经验公式[7] (6) 经过一段时间的演化后,质量较大子星膨胀并充满其洛希瓣体积,系统由分离阶段进入半分离阶段,开始以热时标进行物质交换过程,质量较小子星获得质量后演化膨胀充满其洛希瓣并成为质量较大的主星,质量较大子星失去质量后成为较小质量子星并仍然充满其洛希瓣,两子星发生质量反转。系统进入相接阶段,发生物质交换和能量交换过程,直至两子星发生并合。Stepień在模型中采用了Kähler 2004[27]提出的能量交换的处理方法。 图4 Stepień模型的质量—半径图[7] 图中star B为主星,star A为次星,观测数据的主星用星号标注,其次星用钻石符号在图中标注。虚线ZAMS表示理论计算的处于零年龄主序的质量-半径关系,TAMS虚线表示主序末恒星的质量-半径关系。带箭号的实线中,标注star A的为理论模型计算出进入了相接后次星的演化数据,旁边标注star B的为理论演化中主星的数据。与观测数据的规律相符合,成功诠释了Kuiper佯谬。 相接双星理论模型中,由磁制效应引起的星风物质损失和角动量损失或由磁星风导致的星风物质损失和角动量损失、半分离阶段的物质交换、相接阶段的物质交换和能量交换、自转和公转均是理论演化的基本物理过程,现今理论模型已经完全考虑了这些基本物理过程。 假设能量交换与物质交换在相接阶段是独立并分开进行,理论模型获得了热弛豫震荡演化,成功地解释了观测上的周期-颜色规律,而预言存在较多与低质量相接双星具有相同颜色和周期分布的EB型低质量半分离双星。若将能量交换看作是由物质交换后转移的物质所携带的能量,理论演化则消除了震荡现象,出现了从相接进入半相接后不再震荡的现象。为此,物质交换和能量交换是模型中的重要过程,直接影响相接双星的形成和演化。其中研究能量交换的驱动机制和发生地具体过程一直是相接双星理论演化研究中的热点和难点。总之,模型中这些物理过程的假设和处理,对演化结果造成重要影响。分析清楚它们的驱动机制是演化模型的关键,也是当前研究中的主要物理问题。 至今为止,理论模型已经能够解释周期-颜色关系和kuiper佯谬,尚未能完全地解释光变曲线的观测规律。建立和完善相接双星理论演化模型,用于解释低质量相接双星的所有观测现象,是目前研究过程中的难点。 [1] KOPAL Z. The classification of close binary systems[J]. Annales d’Astrophysique. 1955, 18:379. [2] MOCHNACKI S W. Contact binary stars [J]. ApJ, 1981, 245: 650-670. [3] KUIPER G P. On the Interpretation of β Lyrae and Other Close Binaries[J]. ApJ, 1941,93: 133-177. [5] ROBERTSON J A, EGGLETON P P. The evolution of W Ursae Majoris systems[J].MNRAS,1977, 179: 359-375. [9] CSIZMADIA SZ, KLAGYIVIK P. On the properties of contact binary stars[J]. A&A, 2004, 426:1001-1005. [10]LUCY L B. The light curves of W Ursae Majoris stars[J]. ApJ, 1968, 151: 1123-1137. [11]MACERONI C, VAN’T VEER F. The properties of W Ursae Majoris contact binaries: new results and old problems[J]. A&A, 1996, 311: 523-531. [12]YILDIZ M, DOGAN T. On the origin of W UMa type contact binaries-a new method for computation of intial masses[J]. MNRAS, 2013, 430:2029-2038. [13]RUCINSKI S M. The W UMa-type Systems as Contact Binaries. I. Two Methods of Geometrical Elements Determination. Degree of Contact[J]. Acta Astron, 1973, 23, 79-120. [14]RUCINSKI S M. Binaries. II. A- and W-type Systems. The W UMa-type Systems as Contact[J]. Acta Astron, 1974, 24, 119-151. [15]LUCY L B. W UMa systems with marginal contact[J].ApJ, 1976, 205: 208-216. [16]FLANNERY B P. A cyclic thermal instability in contact binary stars[J].ApJ, 1976, 205: 217-225. [17]ROBERTSON J A, EGGLETON P P. The evolution of W Ursae Majoris systems[J]. Mon Not Roy Astron Soc,1977,179:359-375. [20]EGGLETON P P. Evolution of very close binaries of low mass[J]. ASPC, 2010,435:151. [21]LI L F, HAN Z W, ZHANG F H. Structure and evolution of low-mass W UMa-type systems[J].MNRAS, 2004, 351: 137-146. [22]LI L F, HAN Z W, ZHANG F H. Structure and evolution of low-mass W Ursae Majoris type systems-II. With angular momentum loss[J].MNRAS, 2004,355:1383-1398. [23]LI L F, HAN Z W, ZHANG F H. Structure and evolution of low-mass W Ursae Majoris type systems-III. The effects of the spins of the stars[J].MNRAS, 2005,360:272-281. [25]SONG H F, HUANG R Q, BI S L.A Model for Contact Binary Systems[J]. Chin J Astron Astrophys, 2007,7:539-550. [26]SONG F, HUANG R Q. Test of a low-mass contact binary model by comparing the relations obtained from theory with those from observations, Sci China Ser G-Phys Mech Astron., 2012, 55(4):706-716. (责任编辑:周晓南) The Research Progress of Low-Mass Contact Binary SONG Fen1,2 ( 1.College of Science, Jimei University, Xiamen 361000,China;2.Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences,Kunming 650011,China) The observational and theoretical researches of close binary are one of stellar physical research hotspots. It is the difficult problem of binary evolution to explain observational phenomena of low-mass contact binary. By summarizing observational materials(from light curve and physical parameters) and theoretical model of low-mass contact binary, some main questions in this research field were presented, this work was important to improve binary evolution theory. binary; contact binary; binary evolution 1000-5269(2016)02-0045-06 10.15958/j.cnki.gdxbzrb.2016.02.11 2015-09-08 国家自然科学基金面上项目资助(11373020);中国科学院天体结构与演化重点实验室项目资助(B615015);集美大学校级预研基金项目资助(C613030) 宋芬(1985-), 女,讲师,博士,研究方向:恒星物理, Email:fsong@jmu.edu.cn. 宋芬,Email:fsong@jmu.edu.cn. P142.9 A

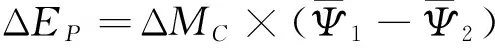

3 结论

