镍基变形高温合金本构分析研究进展①
俞 丹,王 莹,陈 悦,王 珏
(南京工程学院材料工程学院, 江苏 南京 211167)
镍基变形高温合金本构分析研究进展①
俞丹,王莹,陈悦,王珏
(南京工程学院材料工程学院, 江苏 南京211167)
本构分析是计算镍基变形高温合金热加工外载荷,预测热变形组织的有效方法,为实际生产中加工工艺的制定提供理论参考,同时也可以为有限元法模拟加工过程提供重要数据。综述了镍基变形高温合金本构方程的研究现状,包括目前广泛采用的本构方程的形式及其推导过程,以及在流变应力模型,动态再结晶模型等方面的研究进展。
镍基高温合金; 本构方程; 流变应力模型; 动态再结晶模型
引 言
采用数学的方法对实验结果进行定量处理,获得精确的数学模型是本构分析的实质,这些数学模型又叫本构方程,本构方程反映了流动应力、应变、应变速率、变形温度以及变形组织之间的关系。准确的本构方程是建立具有预测性的材料塑性成型模型的核心问题。这些模型既包括对流变曲线的描述,也包括对组织的描述与预测(例如关于动态再结晶的本构方程),最终目的有两个:一是通过本构方程的计算和外推,建立流变应力与变形参数的关系,进而计算出精确的变形抗力;二是通过与变形组织相结合,建立组织演化模型,分析变形组织演化规律。以上两点都可以通过与计算机有限元技术相结合提高计算速度和精度,获得直观的可视化结果。
研究者们通常通过三种途径来获得材料塑性变形的本构方程:①假设特别的变形机制,用相关的材料参数建立与这种机制相对应的方程[1]。②用一标量内参来代表塑性变形时由材料内部状态产生的各向同性变形阻力,从而获得描述大塑性变形的一阶本构模型[2-3]。③用实验测量一定应变速率、温度范围内的流变应力数据,进而根据这些数据建立相应的本构方程。虽然人们总是希望选择少数几种类型的本构模型适用于所有的材料和热加工参数范围,但事实证明目前还难以做到。因此,根据材料的流变应力关系曲线特征,合理选用经验方程作为材料模型仍然不失为一种有效途径。
本构分析在镍基高温合金方面的应用十分广泛。例如,通过建立模型研究化学成分对镍基合金形变的影响[4],或者是采用本构分析方法研究镍基合金再结晶晶粒尺寸与形变参数之间以及峰值应力,变形温度,应变速率之间的函数关系[5]。还可以通过实验直接研究镍基合金的本构特性[6]。除此之外,还有许多针对镍基高温合金的研究采用了本构分析的方法[7-11]。
1 流变曲线的本构分析
热变形条件下,流变曲线的形状特征由加工硬化和动态软化这两种机制的相互作用所决定。大多数镍基高温合金的流变曲线表现出以下特征:第一阶段加工硬化占主导地位,应力值随应变量的增加而线性增加;第二阶段流变应力增大的趋势逐渐减缓,达到峰值应力后又逐渐降低;第三阶段的流变曲线则相对平稳。值得注意的是,镍基高温合金的峰值应力并没有奥氏体不锈钢那么明显,并且其具有较低的层错能,DRX是其主要的软化机制[7]。
1.1流变应力与变形温度和应变速率的关系
大量的本构研究是建立流变应力与变形条件之间的定量关系,进而预测不同工艺条件下的外载荷。根据试验数据拟合建立的热变形本构方程是利用刚塑性有限元方法对金属加工过程进行数值模拟的前提条件,可作为热变形工艺参数选择的重要依据,也可用作耗散结构理论的动力学方程来确定变形稳定区[12-14]。
许多文章报道了流变应力与变形温度和应变速率之间的定量关系,通常采用Arrhenius型本构方程,其中Sellars 和 Tegart 提出的本构模型应用最广,其主要包括3种形式[15-16]:
1)在低应力水平下
(1)
2)在高应力水平下
(2)
3)在所有应力水平下
(3)
式中α,β,A为与温度无关的常数;n为应力指数,且满足α=β/n;Q为材料变形激活能;R为摩尔气体常数;T为热力学温度;σ为流变应力。式(1)适用于描述高温低应力状态下的热变形行为;式(2)适用于描述高应力水平下的热变形行为,但在高变形温度而且应变速率小于1 s-1的情况下难以准确地描述高温合金的热变形过程。式(1),(2)如果应用于不适当的应力及温度条件,则会造成较大误差。因此,Sellars和Tegart在公式(1),(2)基础上创立了公式(3),即含双曲正弦的关系式,该式能够在比较宽的应力范围内,比较精确地描述材料变形时的行为。图1是建立形如式(3)的本构方程流程图[17-18]。
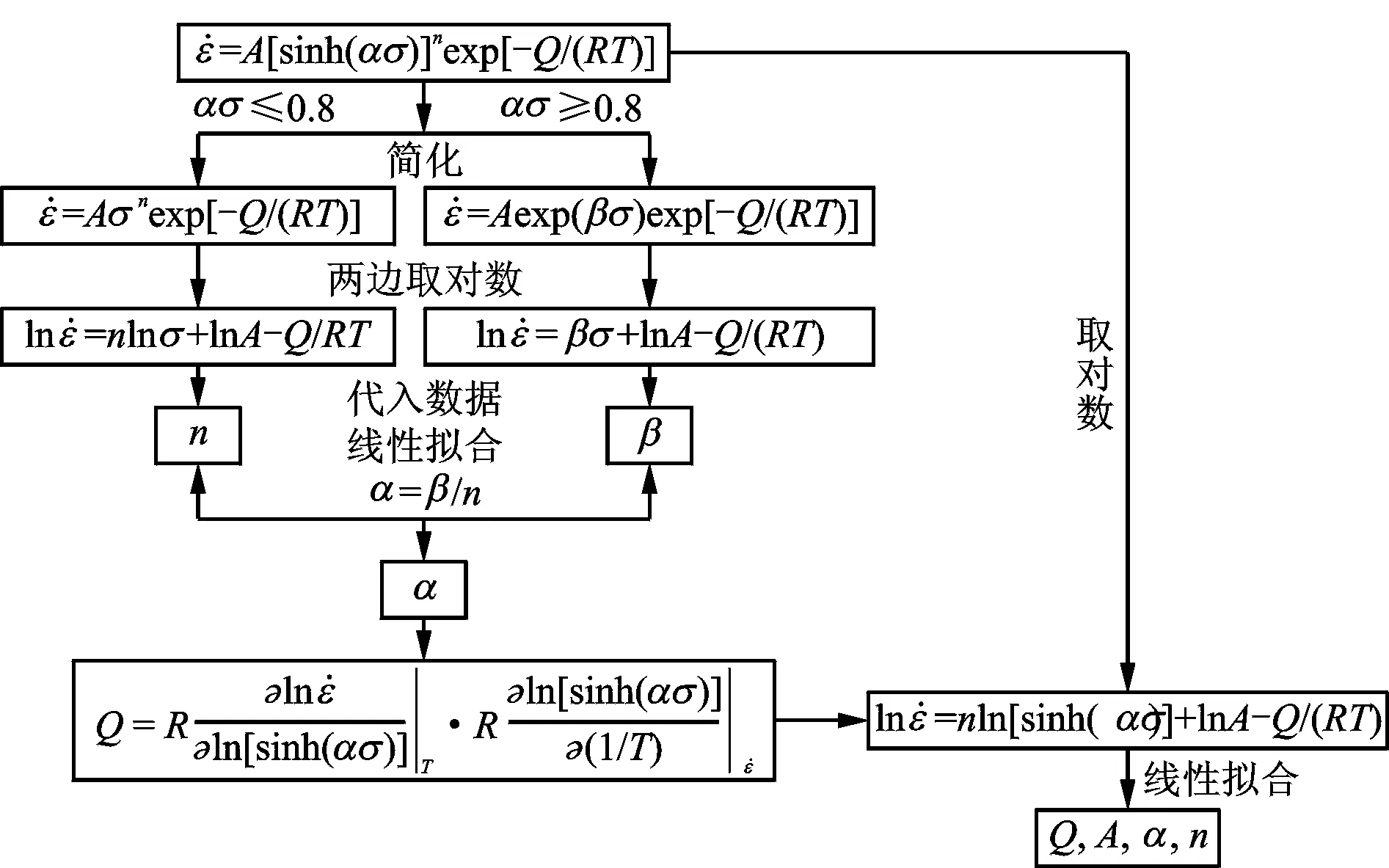
图1 建立本构方程流程图
选定所采用热模拟实验的数据,由于流变应力的精度受测量精度的影响较大,故一般用峰值应力代替稳态流变应力。在不同变形条件下对合金流变应力的实验值和计算值进行比较,若模型计算和实验测得的峰值应力吻合较好,说明所选择的本构方程正确。
不同种类高温合金成分的区别,会从本质上影响本构方程参数的取值。Bi[4]等在镍基高温合金流变应力模型的研究中指出:合金的化学成分对激活能Q和A的值都有一定的影响,不同的合金元素对激活能Q的影响程度不同。因此,为了进一步完善镍基高温合金的本构方程,Bi等建立了如下表达式
(4)
其中,
Bi等还指出lnA与Q存在明显的线性关系
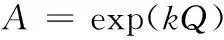
(5)
其中,k=8.18383×-5J-1。
Wang[5]等运用上述激活能Q的表达式,将740H的激活能Q与其他镍基高温合金相比较,发现740H的激活能Q与690,G3合金的激活能相接近;但其值比Waspaloy,Udimet720 和C276合金小。研究认为表观激活能Q代表着变形过程中硬化和软化的平衡,同时为与速率控制机制有关的原子重组提供信息。因为通过实验得到的Q值与自扩散激活能的值相接近,所以人们曾用空位迁移和位错攀移理论来解释Q。Wang[7]等通过计算发现,GH738的表观活化能的平均值比其合金元素的自扩散活化能值高,这可能与位错湮没、DRV和DRX、沉淀析出等相互作用有关,并且GH738的表观活化能的平均值与被广泛应用于超临界电厂蒸汽管道的P92钢相接近。
1.2初始晶粒尺寸对本构方程的影响修正
目前大多数合金的本构关系模型中均未考虑晶粒尺寸的影响,为了能够精确预测变形过程中的流变应力值,建立含有初始晶粒尺寸参量的本构方程是很有必要的。杨亮[19]等利用物理模拟实验方法对具有不同晶粒尺寸的690合金试样进行热压缩变形实验,获得了合金的流变应力数据,并对合金变形后的组织特征进行了分析,建立了包含初始晶粒度参数的本构关系模型,继而完善了690合金的热变形本构方程。图2是含有初始晶粒尺寸参量的本构方程流程图。模型计算和实验测得的流变应力值吻合较好,说明所建立的含有初始晶粒尺寸参量的690合金热变形本构关系模型能够很好地预测晶粒尺寸变化对流变应力的影响。
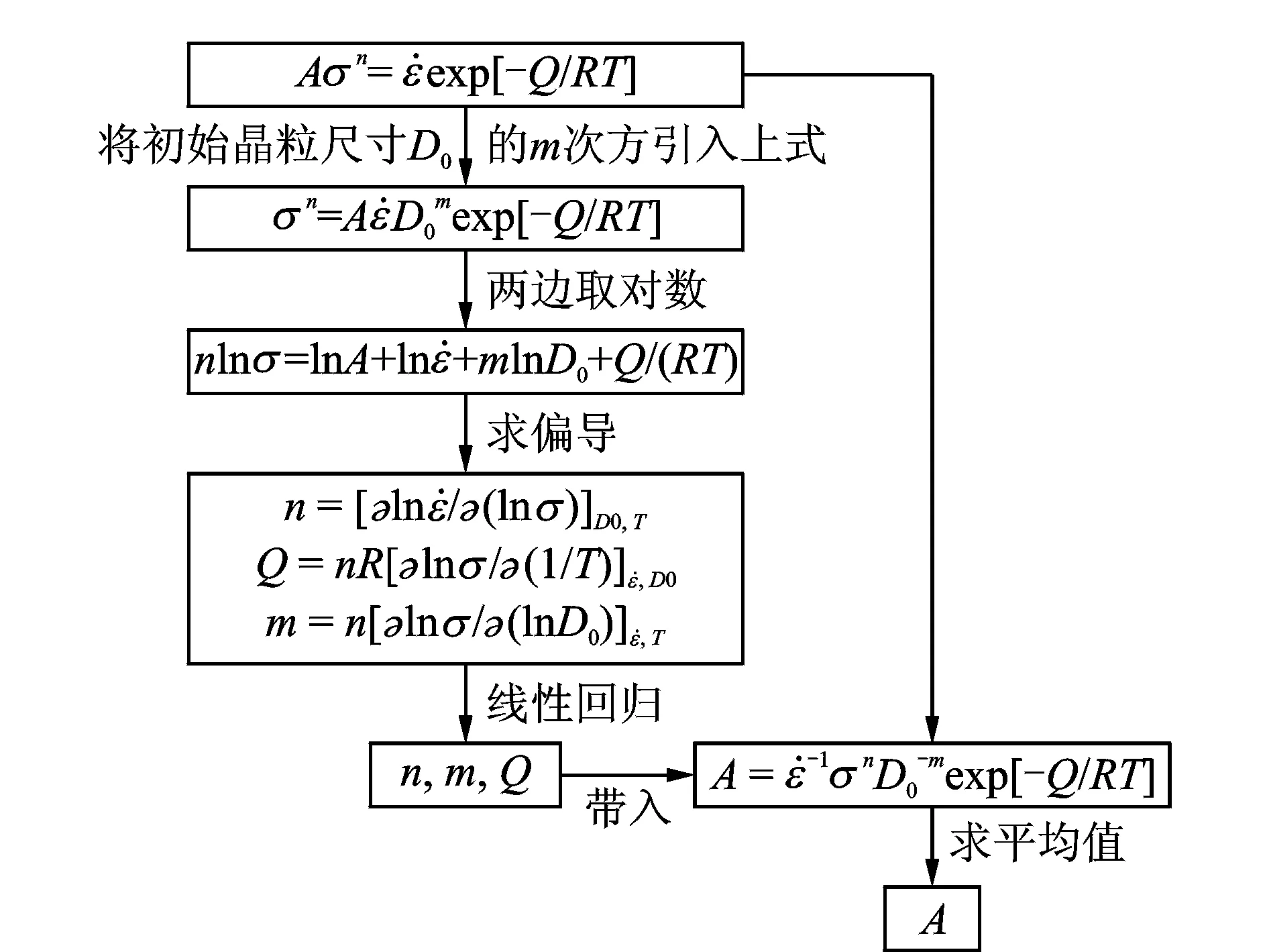
图2 含有初始晶粒尺寸参量的本构方程流程图
1.3流变应力与应变量的关系
应变量也是影响流变应力的一个重要因素。而式(3)只是表示变形温度、应变速率和流变应力这三者的关系,而没有考虑应变量对应力的影响。为建立更准确的本构模型,应在(3)的基础上加入应变量补偿,以此构建变形温度、应变速率、应变量和应力之间的关系。有的文献[20]按照690合金各材料常数的确定方法,在应变量为0.05~0.65范围内,以0.05为最小间隔,分别求出不同应变量下的β,n,α,Q,lnA的值,然后用式(6)进行五次多项式拟合,从而获得β,n,α,Q,lnA与应变量ε的多项式函数关系。
(6)
利用式(6)确定各材料常数之后再通过式(3)计算得到不同应变量下的流变应力,也可以通过式(6)得到σ与Z参数之间的关系,其中Z参数综合了变形温度和应变速率对材料组织的影响:
(7)
(8)
这样就可以确定加入应变量补偿后的690合金热变形本构方程
(9)
2 热变形组织演化的本构分析与模型
2.1热变形组织演化本构分析的可行性
材料在热变形过程中除了宏观性质发生改变外,材料的微观组织也会发生改变。根据真应力-真应变曲线可以推断材料在热变形过程中的微观组织演化方式,同时也可以判断热变形工艺参数的选择是否合理。
中国特色扶贫开发道路尽管是在逐步探索中形成的,但这种探索并不是盲目的探索,而是在继承发展马克思主义反贫困理论的基础上成长起来的。
图3是杨亮等[20]研究的690合金在 1150 ℃以1 s-1的应变速率变形时的真应力-真应变曲线及显微组织。由图3可知:a点处的应变量较小,此时在三叉晶界处开始发生动态再结晶;当应变量达到峰值b点处时,原始奥氏体晶粒周围开始形成细小的动态再结晶晶粒;当应变量增加到c,d点处时,原始奥氏体晶粒逐渐被动态再结晶晶粒所取代;当应变量达到e点处时,再结晶晶粒基本完全取代了原始晶粒,此时动态再结晶基本完成。流变曲线和微观组织之间有对应关系,所以可以通过对流变曲线进行本构分析来研究热变形微观组织的变化。
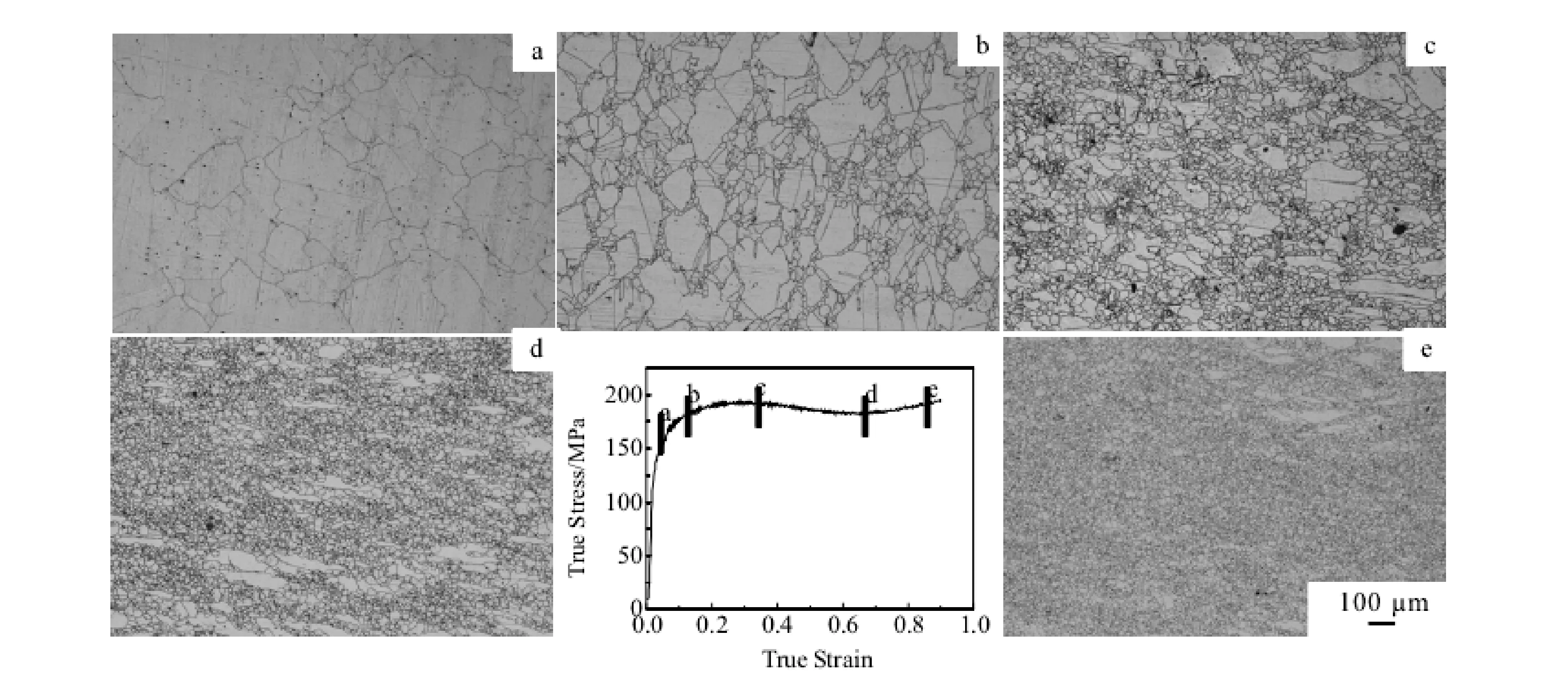
图3 690合金在1150 ℃以1 s-1的应变速率变形时的真应力-真应变曲线及显微组织演变[20]
2.2热变形动态再结晶的本构模型
动态再结晶是镍基高温合金热变形时动态软化的主要方式。在热变形过程中,材料动态再结晶在宏观上主要通过流变应力曲线的形状来判断。动态再结晶的发生与否与变形程度、应变速率及变形温度等有关。
2.2.1动态再结晶临界条件的确定
材料在热变形过程中能否发生动态再结晶,宏观上取决于变形条件,微观上取决于位错的密度及分布,即当位错密度达到某个临界值时材料才开始发生动态再结晶,此时对应的应变为临界应变。
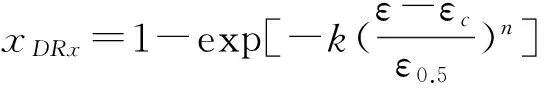
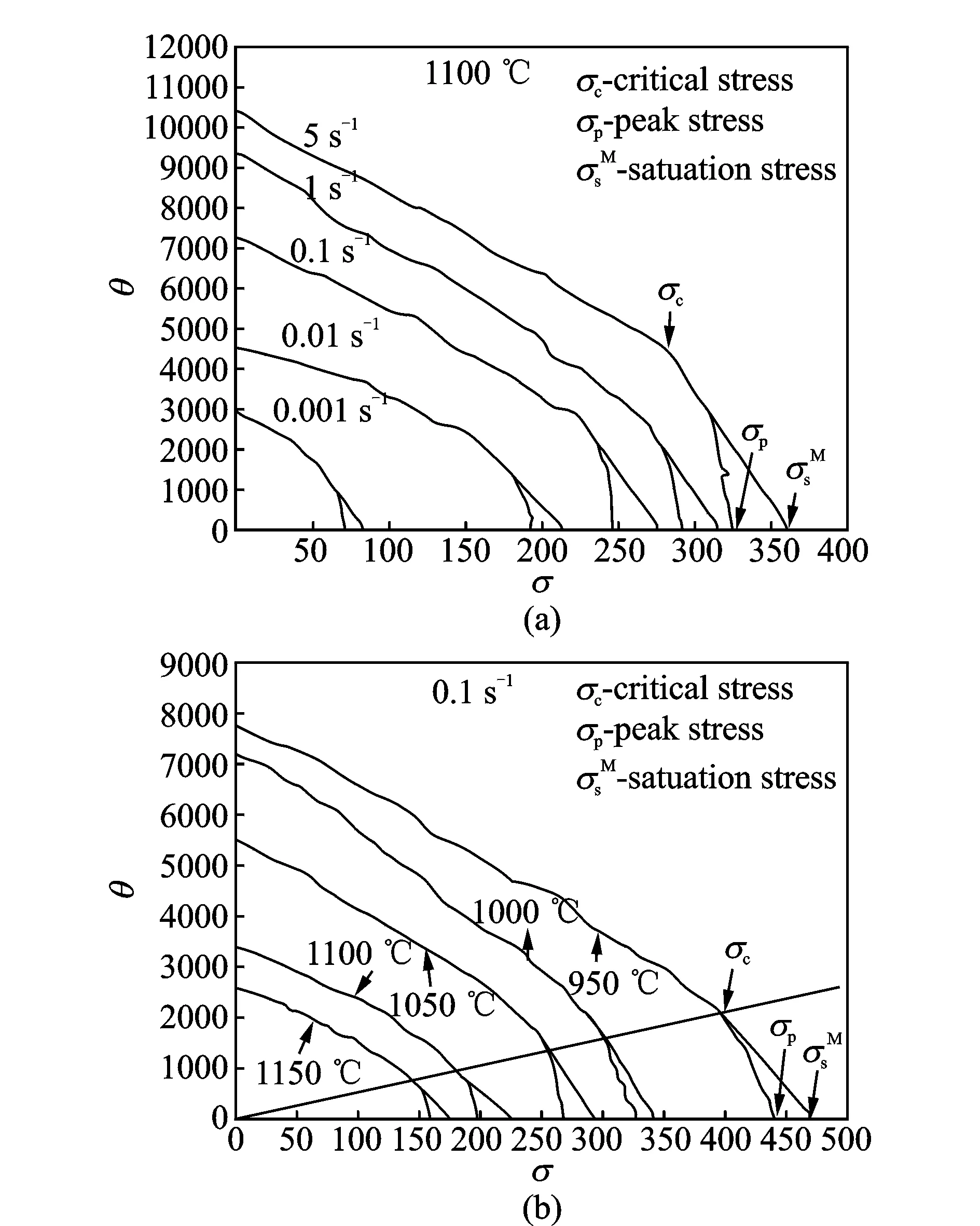
图4 GH625合金硬化率和应力的关系曲线[23]
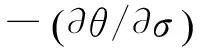
(10)
2.2.2动态再结晶动力学模型
动态再结晶体积分数可以采用金相观测的方法直接测定,也可以通过热模拟实验得到的真应力一真应变曲线间接地确定,而后者常用来对前者测定的结果进行验证[24]。目前,学者们普遍采用 Avrami 方程描述材料动态再结晶体积分数与应变量的关系,并在镍基高温合金中得到广泛应用。Avrami方程表达式[25]
(11)
式中k,n为材料常数;ε0.5为发生50%再结晶的变形量。对公式(11)两边取对数得
(12)
式中ε,εc,ε0.5可根据以下公式测得[26]
(13)
式中xDRx为该应力状态下动态再结晶体积分数实验值,σ为真应变为ε时的真应力,σv为真应变为ε时估计的动态回复应力,σvs为动态回复饱和应力,σss为动态再结晶的稳态流变应力。具体意义及位置如图5所示。对得到的再结晶体积分数-应变量关系曲线进行插值运算,得到再结晶体积分数为50%时所对应的应变量ε0.5。
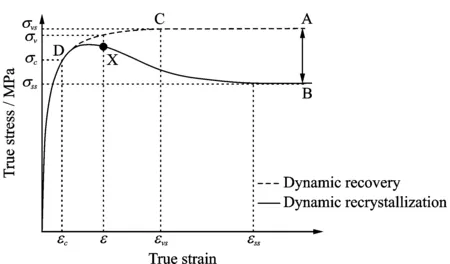
图5[26] 应力-应变曲线法各参数示意图
为确定式(12)中的k和n的值,对ln[-ln(1-xDRx)]-ln[(ε-εc)/ε0.5]进行线性回归。取各直线截距和斜率的平均值,将所求得的k和n值代入式(11),即可得出动态再结晶的动力学方程。
刘毅[27]等采用动态再结晶动力学方程(J-M方程)来进一步分析变形温度对Haynes 230 合金热变形组织的影响
(14)
式中XR为再结晶体积分数,G为再结晶长大速率,N为再结晶形核率,t为动态再结晶时间。再结晶生长速率G和再结晶形核率N都是随着变形温度的升高而增大,由式(14)可知,再结晶体积分数XR继而增加。
MEDINA[28]等在对低合金奥氏体钢动态再结晶模型的研究中提出公式(11)中的k和n并不是常数,而是取决于量纲常数Z/A。通过实验数据得出了k,n关于Z/A的函数,从而获得了与变形温度,应变速率以及原始晶粒尺寸有关的动态再结晶动力学模型。该模型可以被应用到所有的低合金和微合金化钢。
2.2.3动态再结晶晶粒尺寸模型
动态再结晶晶粒尺寸主要由变形温度、应变速率决定,研究者们一般采用 Sellars 等提出的幂函数关系来描述[29]
(15)
式中A,n为实验常数,对式(15)两边取对数得
lnD=lnA-nlnZ
(16)
对lnD-lnZ采用线性回归处理即可求出常数A和n。
从式(16)中可以看出随着Z值的增加,晶粒尺寸减小。如果想要获得细晶组织,必须提高Z值,Z值的增加应当在发生动态再结晶的温度范围内,采用增加应变速率来获得。
刘东[30]等采用应变速率的多项式确定参数F1和F2来建立GH4169合金的动态再结晶晶粒尺寸模型
(17)
式中T为变形温度;Tp为D相溶解温度。该式可以很好地反映晶粒尺寸与应变速率之间的复杂关系。
Wang[5]等人在740H镍基高温合金热加工特性的实验研究中指出当应变速率小于1 s-1时,动态再结晶晶粒尺寸变化符合公式(15)的基本规律,而当应变速率大于1 s-1时,动态再结晶晶粒尺寸则表现出相反的变化趋势,原因可能是大的应变速率可能导致不可忽视的变形热,从而促进动态再结晶晶粒尺寸的长大。通过实验数据的研究和计算,提出以下表达式
(18)
3 结束语
作为航空航天、石油动力等行业的关键材料,变形高温合金的国产化势在必行,而研究变形高温合金的本构模型对镍基高温、耐腐蚀合金材料的热变形方式都有指导意义。本构方程作为预测变形高温合金热变形过程的核心,越来越引起科研学者们的重视。目前国内外已经对高温合金本构模型的机理进行了一定深度的研究,但仍存在机理不够完善的问题需要进一步深入。
[1]Frost H J, Ashby M F. Deformation mechanism maps: the plasticity and creep of metals and ceramics[M]. New York: Pergamon Press, 1982.
[2]Brown S B, Kim K H, Anand L. An internal variable constitutive model for hot working of metals[J]. International Journal of Plasticity, 1989, 5(2): 95—130.
[3]Dedai C S, Curran D R.Constitutive Laws for Engineering Materials; Theory and Applications[M]. North Holland: Elsevier Science Publishing Co. Inc.,1987.
[4]Bi Z, Zhang M, Dong J, et al. A new prediction model of steady state stress based on the influence of the chemical composition for nickel-base superalloys[J]. Materials Science and Engineering: A, 2010, 527(16): 4373—4382.
[5]Wang J, Dong J, Zhang M, et al. Hot working characteristics of nickel-base superalloy 740H during compression[J]. Materials Science and Engineering: A, 2013, 566: 61—70.
[6]Wang Y, Li Z, Xu W Y, et al. Constitutive characteristic of hot deformation for spray formed superalloy GH738[C]. Materials Science Forum. Trans. Tech. Publications, 2013, 747: 569—574.
[7]WANG L, YANG G, LEI T, et al. Hot deformation behavior of GH738 for a-USC turbine blades[J]. Journal of Iron and Steel Research (International), 2015, 11: 1043—1048.
[8]Jiang H, Dong J, Zhang M, et al. Hot deformation characteristics of alloy 617B nickel-based superalloy: A study using processing map[J]. Journal of Alloys and Compounds, 2015, 647: 338—350.
[9]刘洋, 陶宇, 贾建. 镍基粉末高温合金 FGH98 流变曲线特性及本构方程[J]. 航空材料学报, 2011, 31(6): 12—18.
[10]李莎, 曾莉. GH4700 镍基高温合金的高温塑性变形性能[J]. 太钢科技, 2013 (3): 21—25.
[11]张伟红, 孙文儒, 华培涛, 等. GH4145 合金热变形行为研究[A]. 第十二届中国高温合金年会论文集[C], 2011.
[12]杨亮, 董建新, 张麦仓. 690 合金高温变形行为与动态再结晶模型[J]. 稀有金属材料与工程, 2012, 41(4): 727—732.
[13]张付军, 周晚林, 陈文豪. GH4169 合金不同热变形条件下的流变应力研究[J]. 机械制造与自动化, 2014, 43(5): 203—205.
[14]李卿, 郭鸿镇, 王彦伟, 等. GH4049 合金的热变形行为及组织演变[J]. 材料工程, 2014 (12): 55—59.
[15]张冬旭, 温志勋, 岳珠峰. GH3230 高温合金热变形行为及本构模型研究[J]. 稀有金属, 2014, 6: 986—992.
[16]吾志岗, 李德富. GH625 镍基合金的高温压缩变形行为及组织演变[J]. 中国有色金属学报, 2010, 20(7): 1321—1327.
[17]汪杰. 新型喷射成形镍基高温合金热变形行为研究[D]. 成都:西南交通大学, 2014.
[18]Liu Y, Hu R, Li J, et al. Deformation characteristics of as-received Haynes230 nickel base superalloy[J]. Materials Science and Engineering: A, 2008, 497(1): 283—289.
[19]杨亮, 董建新, 张麦仓. 晶粒度对 690 合金热变形特性的影响[J]. 稀有金属材料与工程, 2012, 8: 1477—1482.
[20]杨亮. 690合金变形行为及组织与工艺控制研究[D][D]. 北京: 北京科技大学, 2011.
[21]Poliak E I, Jonas J J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization[J]. Acta Materialia, 1996, 44(1): 127—136.
[22]Semiatin S L, Jonas J J. Formability and workability of metals: plastic instability and flow localization[J]. American Society for Metals, 1984,44(1): 299.
[23]刘志超. GH625 合金的热变形行为及动态再结晶研究 [D]. 长沙: 中南大学, 2011.
[24]彭海健. GH690 合金热变形行为及管材热挤压机理研究[D]. 北京:北京有色金属研究总院, 2014.
[25]何文武, 刘俊伟, 赵晓东, 等. 高温合金 800H 的动态再结晶及其模型的建立[J]. 钢铁研究学报, 2014, 26(10): 55—59.
[26]张云. GH4742 合金热变形行为及动态再结晶研究[D]. 东北大学, 2013.
[27]刘毅, 许昆, 罗锡明, 等. Haynes230 合金热变形组织演化规律研究[J]. 稀有金属材料与工程, 2013, 42(009): 1820—1825.
[28]Medina S F, Hernandez C A. Modelling of the dynamic recrystallization of austenite in low alloy and microalloyed steels[J].Acta Materialia,1996,44(1):165—171.
[29]刘建涛, 张义文, 陶宇, 等. FGH96 合金动态再结晶行为的研究[J]. 材料热处理学报, 2006, 27(5): 46—50.
[30]刘东, 罗子健. GH4169 合金热加工过程中的显微组织演化数学模型[J]. 中国有色金属学报, 2003, 13(5): 1211—1218.
2016-02-25
江苏省大学生科技创新项目(201511276061x);南京工程学院大学生科技创新项目(BX20160233)
俞丹(1995—),女,本科生。电话:18351988597;E-mail:1563863193@qq.com
TG113.25

