基于仿射变换的局部特征匹配算法
戚海想(四川大学计算机学院,成都610065)
基于仿射变换的局部特征匹配算法
戚海想
(四川大学计算机学院,成都610065)
0 引言
图像匹配是计算机视觉和图像处理中一项非常重要的研究内容,在目标跟踪、模式识别、遥感图像和医学图像等领域中有非常广泛的应用。发展至今,图像匹配不断取得显著的研究成果,已经有很多经典的图像匹配算法,例如SIFT[1],SURF[2],Harris[3],MSER[4],ASIFT[5]等。该类匹配方法首先提取两幅待匹配图像中的特征点,这些特征点用其空间结构关系进行描述,然后通过这种相似的空间结构关系找到匹配特征点对。其中SIFT算法应用最广泛,该匹配方法取得的特征点对于尺度、旋转和焦距变化具有良好的适应性,对光照、噪声干扰具有很强的鲁棒性。然而该算法在匹配点对数量和运算的实时性方面有一定的局限性。在本文中,提出一种改进的基于仿射变换的局部特征匹配算法,该算法利用Lowe在SIFT算法中提出的128维描述子对特征点进行描述,在特征匹配时将一幅图片划分成很多的小区域块,每个小区域块都具有不同的仿射性质,在小区域块中选出符合一定条件的三点对计算仿射变换矩阵,参考图像上该区域内的每个特征点利用仿射变换矩阵映射到测试图像中,然后在仿射点邻域进行局部匹配,实验证明改进后的算法能够增加匹配点对数量,同时也能保持较高的匹配精度。
1 SIFT算法
SIFT算法是经典的图像匹配算法,主要包括以下处理过程。
1.1极值点检测
一个二维图像在不同尺度下的尺度空间可以用高斯函数与图像的卷积表示:

σ为高斯函数的标准差,*为卷积符号,I(x,y)表示图像。
尺度空间的局部空间上的最大值或最小值具有很好的稳定性,利用LOG算子检测极值点,DOG算子是归一化的LOG算子的近似和简化,通过DOG算子检测极值点将大大减小时间复杂度。DOG算子的表示如下:
D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))*I(x,y)
=L(x,y,kσ)-L(x,y,σ)(3)
在检测极值点时,需要将其与同一尺度相邻的8个像素,以及上下两个相邻尺度相同位置上的3×3个像素,共26个像素进行比较,从而检测出局部极值点,尺度空间中检测到的极值点具有尺度不变性。在已经检测到的极值点去除一些不稳定的点,即低对比度极值点和不满足一定条件的边缘响应点。
1.2计算特征点方向
利用特征点邻域内像素点的梯度模值和梯度方向,最终寻找到特征点的主方向。梯度模值和梯度方向计算公式如下:
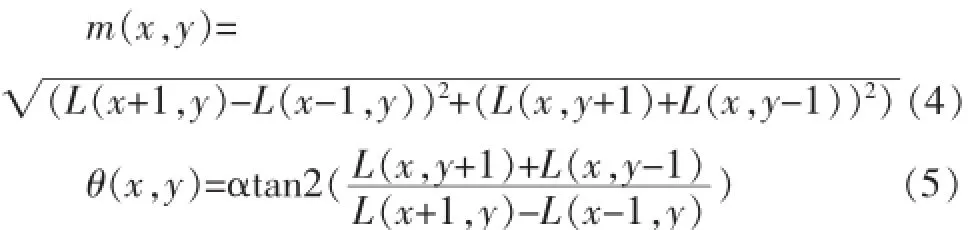
用直方图统计特征点邻域内像素点的梯度方向,方向直方图的范围为0~360度,每10度一柱,共36柱,越远离特征点的像素对其贡献越小,利用像素点的梯度幅值乘以高斯下降函数,最终生成梯度直方图。直方图的峰值代表该特征点的主方向。
1.3计算特征点描述子
每个特征点有三个信息:位置,尺度和方向,由此可以确定一个特征区域。将特征点的邻域窗口分成4× 4的小方块,在每个小方块中形成梯度方向直方图,每45度一柱,共有8柱,这样就可以形成一个128维的特征描述向量。
1.4特征匹配
求参考图像中的每个特征点在测试图像的特征点集中最近与次近的特征点;若最近与次近的比率小于某个给定阈值,则认为正确匹配,否则不匹配;这里的最近与次近定义为特征点的描述符向量的欧氏距离。
2 LMA算法
2.1三点对的选取
在三个特征点对计算仿射变换矩阵时,需要判断三点对是否能够计算出比较准确的仿射变换矩阵。三个特征点形成的三角形不能太大,也不能太小和太扁,三角形太大使局部性匹配得不到很好的提现;太小使得三个点的坐标非常相近,可以近似看成一个点,三角形太扁可以近似看成三点共线,这两种情况都会导致邻域上的特征点不能利用该仿射变换矩阵准确找到其匹配特征点。基于以上情况,需要存储参考图像上任意两个特征点之间的距离信息,使三个特征点之间的距离既不能太远又不能太近。设任意两个特征点pi,pj;其欧氏距离如下:

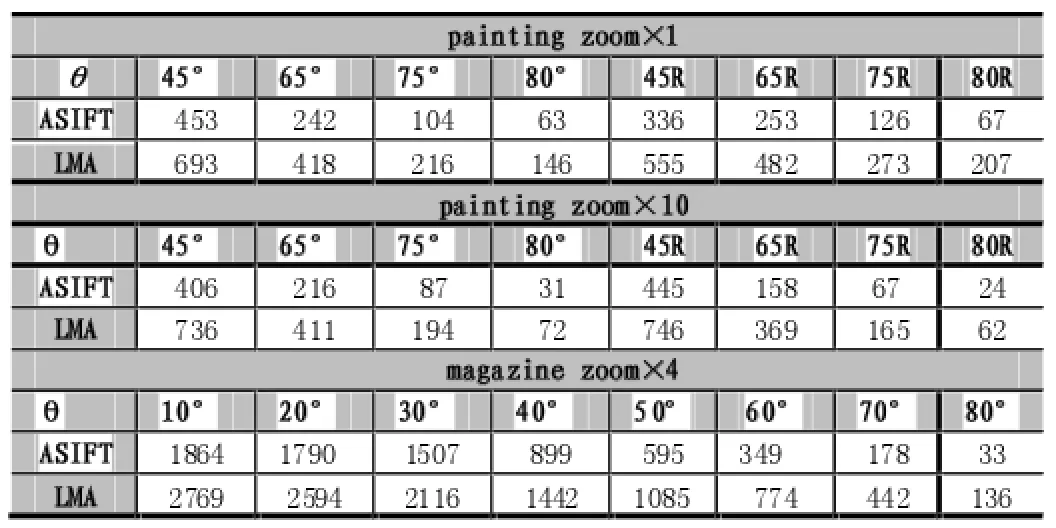
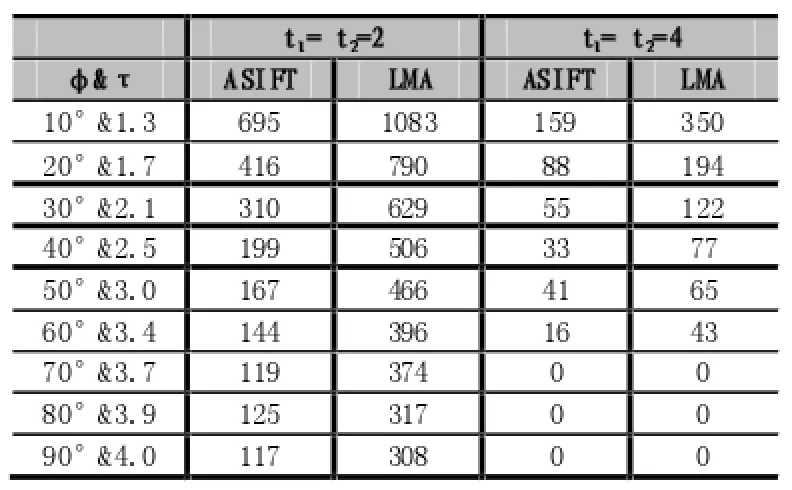
(xi,yi)代表特征点pi的坐标,(xj,yj)代表特征点 pj的坐标。如果pi≠pj并且 Dl 设任意三个点pi,pj,pk,如果它们是三点对在同一图片上的三个特征点,则它们必须是不共线的。 并且,这三个特征点形成的三角形区域不能太扁平,因此三角形顶点之间必须满足公式(8),在公式(8)中,T1为某一给定阈值。 2.2计算仿射变换矩阵 平面图像上的仿射变换是一种二维坐标到二维坐标上的线性变换,能够保持二维图形的平直性和平行性,仿射变换包含一系列的原子变换,包括平移、放缩、旋转等。仿射变换的表达式可以表示为: (x,y)代表参考图像上特征点的坐标,(x',y')代表测试图像上特征点的坐标,表示放缩和旋转,表示平移。 公式(9)也可以表示成以下形式: 最终表示为如下形式以求出仿射变换矩阵的6个参数: 2.3局部区域内寻找匹配特征点 在参考图像上,对于已经成功找到其匹配特征点,并且满足2.1所述的三点对求取仿射变换矩阵条件的三个特征点,要在其邻域内寻找未匹配的特征点。每在邻域内找到一个未匹配的特征点k,利用相应的仿射变换矩阵计算特征点k映射在测试图像上的点坐标: 其中(kx,ky)为特征点k的坐标,(kx',ky')为映射点的坐标。 在测试图像上,以映射点(kx',ky')为中心,T2为半径的圆形区域内寻找特征点,T2为某一给定阈值。将邻域内找到的所有特征点生成KD-Tree,利用SIFT的匹配策略找到特征点k的匹配特征点。 2.4LMA算法处理步骤 参考图像上,特征点的集合为R,任意一特征点ri∈R,0 (1)在参考图像上,访问集合R中的一个特征点,若该特征点已经成功匹配,则继续访问R中的下一个特征点,直到找到一个未匹配的特征点p。 (2)将测试图像上的所有特征点生成KD-Tree,利用SIFT的特征点匹配策略寻找该特征点的匹配点。若未找到匹配点,则转到步骤(1),若找到匹配点,将该匹配点对作为三点对的第一对,然后寻找另外两对匹配点对,如果mark集合(mark集合中存有未作为三点对用来计算仿射变换矩阵的匹配点对)中的匹配点对数量少于2个,则转至步骤(4)。 (3)在已经成功匹配但是未形成三点对的mark集合中,寻找满足三点对选取条件的2对匹配点对 ,若成功找到,则将这2对匹配点对从mark集合中删除,若最终未找到,则转至步骤(4),否则转至步骤(5)。 (4)顺序访问集合R中在步骤(1)剩下的未访问且未找到匹配点的特征点,将测试图像上的所有特征点生成KD-Tree,利用SIFT的特征点匹配策略寻找其匹配点,直到找到2个满足三点对选取条件的匹配点对。将成功找到匹配点但未与特征点p构成三点对的匹配点对集转至(6)进行处理。若未找到2个匹配点对与特征点key形成三点对,则转至步骤(1),否则,与特征点p形成的三点对转至步骤(5)。 (5)三点对形成的三角形邻域内寻找特征点,每找到一个特征点,利用该三点对形成的仿射变换矩阵 找到其在测试图像上的映射点,以映射点为中心,T3为半径的圆形区域内寻找特征点,T3为某一给定阈值。将找到的所有特征点生成KD-Tree,利用SIFT的特征点匹配策略寻找匹配特征点。将成功找到匹配点的匹配点对集转至步骤(6)。 (6)将匹配点对集形成三点对集,将每一个形成的三点对转至步骤(5)进行处理。尝试将剩下的未形成三点对的匹配点对与mark集合中的匹配点对形成三点对,若能够形成三点对,则删除其中mark中的2个匹配点对,然后将形成的三点对转至步骤(5)进行处理,把最终未形成三点对的匹配点对放入mark集合中。转至步骤(1)。 由于ASIFT通过考虑相机的光轴方向可能发生的所有变化带来的仿射扭曲,将参考图像与测试图像生成多张模拟图像,然后在每张模拟图像上利用SIFT特征描述子提取关键点,最后利用SIFT算法进行特征匹配。ASIFT是基于SIFT原理的,但是提取的关键点比SIFT算法多很多,为了更好地提现本文改进算法的优势,我们在ASIFT算法下进行关键点的提取和匹配,然后用RANSAC[6-7]算法进行错误匹配点的抑制。 选用datasetMorelYu09图像集[5]进行实验测试。在datasetMorelYu09图像集中,有绝对倾斜度图像集和相对倾斜度图像集。 3.1ABsolute tilt tests 油画图像的拍摄光轴为zoom×1和zoom×10,杂志图像的拍摄光轴为zoom×4。摄像机拍摄视角的变化范围为0°到80°。表1为ASIFT算法和LMA算法下的匹配结果。 表1 3.2Transition tilt tests 对于相对倾斜度集,我们使用图像magazine zoom× 4。图像倾斜度分别为t=2和t=4,旋转角从0°到90°。表2为ASIFT算法和LMA算法的匹配结果。图1和图2为两种算法的匹配效果显示。 两种倾斜度分别形成两个图像组,对于每个图像组,第一列为旋转角度和相对倾斜度,第二列、第三列分别为ASIFT算法与LMA算法的匹配点对数。 由表1和表2可以看出,相对于ASIFT算法,改进的特征匹配算法明显增加了特征匹配点的数量。并且改进后的算法对图像的旋转、焦距和光照变化都有很好的适应性和稳定性。 图1 ASIFT算法的匹配结果 图2 LMA算法的匹配结果 表2 改进的匹配算法利用ASIFT算法提取特征点,然后在参考图像的局部区域检测特征点,检测出的特征点利用该局部区域的仿射性质寻找其在测试图像上的匹配特征点。通过对不同光照条件、焦距、拍摄角度的图像进行一系列的实验,实验结果表明本文的改进算法对图像的光照、平移、旋转变换具有显著的改善,能够增加较多的匹配点对。 [1]D.Lowe.Distinctive Image Features from Scale Invariant Keypoint[J].International Journal of Computer Vision,2004:91-110. [2]Bay Herbert,Tuytelaars Tinne,Gool Luc Van.Speeded Up Robust Features[J].Computer Vision and Image Understanding,2008:346-359. [3]Y.Ke,R.Sukthankar.PCA-SIFT:A More Distinctive Representation for Local Image Descriptors[C].Computer Vision and Pattern Recognition,2004:511-517. [4]HARRIS C,STEPHENS M.A Combined Corner and Edge Detection[J].Image Vision Computing,1998:121-127. [5]Jean-Michel Morel,Guoshen Yu.ASIFT:A New Framework for Fully Affine Invariant Image Comparison[J].SIAM Journal on Imaging Sciences,2009:438-469. [6]Luo Juan,Oubong Gwun.A Comparison of SIFT,PCA-SIFT and SURF[J].International Journal of Image Processing,2009:143-152. [7]M.Fischler and R.Bolles.Random Sample Consensus:A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[C].ACM,1981:381-395. Local Feature Matching;Affine Transformation Matrix;Space constraint;Matching Accuracy Local Feature Matching Algorithm Based on Affine Transformation QI Hai-xiang (College of Computer Science,Sichuan University,Chengdu 610065) 1007-1423(2016)05-0058-05 10.3969/j.issn.1007-1423.2016.05.013 戚海想(1989-),女,河南商丘人,在读硕士研究生,研究方向为机器视觉 2015-12-31 2016-02-08 针对SIFT算法中存在一对多和多对一匹配,并最终导致正确匹配被剔除的情况,提出一种基于仿射变换的局部特征匹配算法(LMA)。该方法基于SIFT算法下的匹配点对集,在图像的不同局部区域选择三点对并计算相应的仿射变换矩阵,对于参考图像上的每个特征点,通过距离其最近的仿射变换矩阵找到匹配点,利用RANSAC算法剔除误差较大的匹配点。实验结果表明,通过这种空间约束,改进算法在保证高匹配精度的同时,能够明显增加匹配点数量。 局部特征匹配;仿射变换矩阵;空间约束;匹配精度 Aiming at the situation of the ASIFT algorithm where there are one-to-many,and many-to-one matching,and eventually leading to correct matching are eliminated,proposes a local feature matching algorithm based on affine transformation(LMA).The method is based on the matching key point set under the ASIFT algorithm,in different local areas of an image,chooses three pairs of matching key point and calculates the corresponding affine transformation matrix,for every key point in the reference image,searches for matching key point by the nearest affine transformation matrix,and eliminate the matching key points which have bigger error in the matching key point set by the RANSAC algorithm.The experimental results show that by this kind of space constraint,improved algorithm can obviously increase the number of matching key points,at the same time of ensuring high matching accuracy.


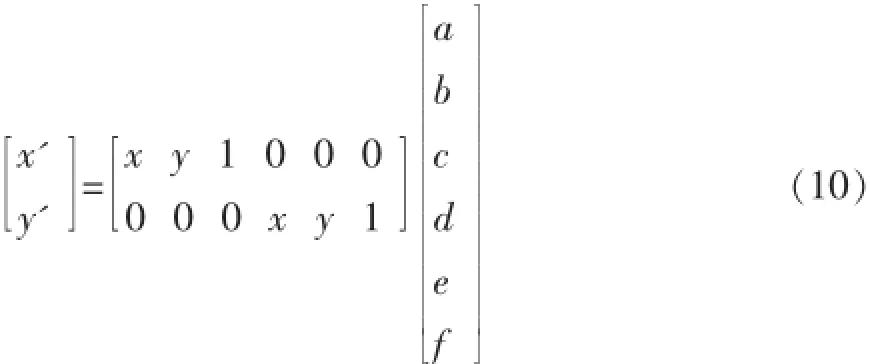


3 实验结果与分析


4 结语

