矮墩连续刚构桥动力特性与地震响应分析
黄国雄
(福州市规划设计研究院 福建福州 350108)
矮墩连续刚构桥动力特性与地震响应分析
黄国雄
(福州市规划设计研究院福建福州350108)
以福州金山大桥复线桥主跨矮墩连续刚构桥为研究对象,通过建立midas空间结构模型,计算分析了矮墩刚构桥的动力特性,同时比较了下部结构参数变化对动力特性的影响。并用反应谱分析了该桥的地震响应。
矮墩刚构;动力特性;地震相应;参数分析
0 引言
在工程实践中,连续刚构桥凭借其施工方便,适应能力强等优点,被广泛应用。设计连续刚构桥时,多将桥墩做成柔性高墩,减小顺桥向的抗推刚度,以改善结构在温度、收缩、徐变、地震等作用下的受力性能。但是,实际上往往由于路线走向、相交道路的标高、通航要求或景观要求,使得连续刚构桥桥墩墩身高度较小,成为了矮墩刚构桥[1]。矮墩刚构桥由于抗推刚度大,柔性小,墩顶和墩底要承受较大的内力,这种结构的桥墩在地震作用下的内力往往是影响结构设计的重要节点[2]。本文通过对福州市金山大桥复线桥主桥的抗震分析,希望对今后同类桥型设计提供一些参考和借鉴作用。
1 工程概况
金山大桥跨越福州闽江,南与金山大道相连,北接上浦路,为福州市区连接仓山区与台江区的重要通道之一。新建金山大桥复线桥位于原金山大桥下游,与老桥间距1m,主桥为变高度混凝土连续刚构箱梁,孔跨布置为60+110+60=230m,采用单箱双室斜腹板箱形截面,下缘采用圆曲线变化,曲线半径为499.23m,主桥支点梁高5.2m,跨中梁高2.4m。主梁顶板宽19.5m,底板宽为9.0m~11.175m,两侧各悬臂3.5m。由于受老桥的标高影响,为保证城市的综合景观,新旧桥桥面标高基本一样,因此主墩墩身采用矩形实心薄壁桥墩,墩高9.5m,墩身横桥向宽度9.0m,顺桥向宽度2.4 m,采用C50混凝土。墩身顺桥向两侧,各设置33根JL32高强度精轧螺纹预应力钢筋,详见图1。
2 动力特性分析
2.1动力计算模型
本桥采用MidasCivil 2012软件建立桥梁结构空间模型进行反应谱抗震分析,主梁、桥墩和承台、桩基均采用空间梁单元模拟。
为使桥梁结构动力计算模型能正确反映结构的实际情况,从而保证结构振型及在E1和E2地震作用下引起内力能得到正确反映.一般情况下,桥梁结构的动力计算模型应满足下列要求:
(1)计算模型中的梁体和墩柱可采用空间杆系单元模拟, 单元质量可采用集中质量代表;墩柱和梁体的单元划分应反映结构的实际动力特性;
(2)支座单元应反映支座的力学特性:对于连续刚构桥墩梁固结边界条件采用了 “刚性连接”,边跨支座采用了”弹性连接”中的“一般连接 ”,其SDX、SDY、SDZ、SRX、SRY、SRZ等刚度使用支座的实际刚度[3];
(3)混凝土结构的阻尼比可取为0.05;
(4)地基的刚度:应考虑用土弹簧模拟桩土效应[4],其支撑刚度采用《公路桥涵地基与基础设计规范》附录P中的m值法计算。具体的有限元模型如图2。
2.2动力特性计算
用子空间迭代方法计算了结构模型的自振特性,取前七阶周期和振型特征列于表1,振型图见图3~图9。

表1 结构模型的自震周期和振型特点
图3一阶模态图4二阶模态

图7五阶模态图8六阶模态
综上分析可以看出,由于主墩墩高较小,刚度较大,边墩采用柱墩,墩高稍高,刚度相对小,结构前面两阶振型主要表现为主梁对称和反对称竖弯;二阶振型中桩基的刚度也对其产生贡献。在第三、四阶的振型中,主要由边墩的对称和不对称侧弯带动主梁的横向对称和不对称弯曲。第五、六阶振型主要是边墩的纵弯。第七阶中出现了刚构主墩的侧向弯曲引起的主梁侧向对称弯曲。以上现象说明了,在该类桥梁中,主墩的面内外刚度均比较大,总体振动不明显,出现的振型也偏后;而主梁的纵向刚度、边墩的纵横向刚度均比较小,因此低阶振型均表现出它们的纵横向振动。
2.3下部结构参数变化对动力特性的敏感性分析[3]
本文试调整了下部结构的尺寸参数,分析其对该类结构动力特性的影响程度。
(1)墩身高度变化对动力特性的影响
在原设计的其他结构及尺寸都不变的基础上,调整承台标高,改变墩身高度,分别按8m、11m。分析后的周期对比如表2。

表2 墩高变化对动力特性的影响对比表
以上对比分析可以看到:
(1)墩高从9.5m增加到11m,前面7阶的阵型均没有改变,还是表现为矮墩刚构的动力特性。第二阶是主梁的一阶反对称竖弯,主墩的纵向弯曲参与了该振型,由于墩高增加,刚度减小,对本阶的周期影响明显,也将改善动力作用下主墩的纵向受力。除此之外的其他几阶振型,由于主墩参与的作用不明显,墩高对周期也影响不大。
(2)当主墩墩高继续减小到8m时,主墩的刚度增大明显,前面六阶基本上为主梁和边墩的振动为主,只有在第七阶时主墩的侧向弯曲参与其中,墩的刚度增大,使得周期有一定的缩短。
3 墩身顺桥向厚度变化对动力特性的影响
在原设计其他结构及尺寸都不变的基础上,调整墩身顺桥向截面厚度,分析结构动力特性,结果详见表3。
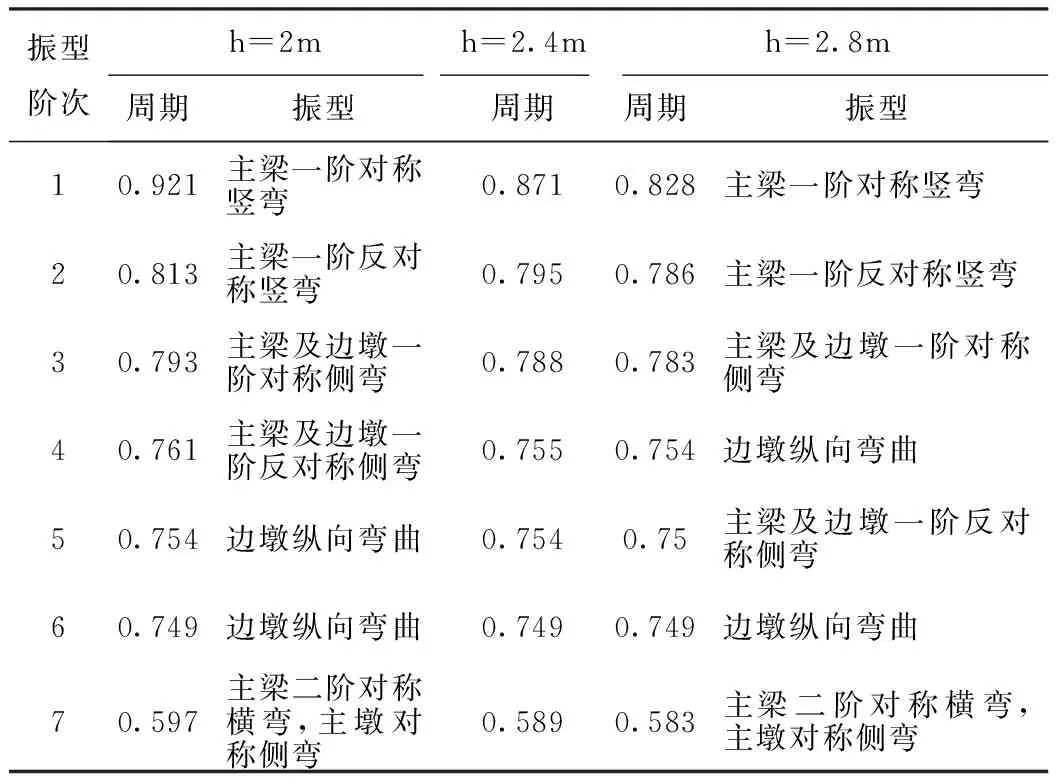
表3 墩身厚度变化对动力特性的影响对比表
以上对比分析可以看到,墩身厚度从2.4m增加到2.8m或减小到2.0m,前面7阶的阵型中,除了主梁及边墩一阶反对称侧弯振型的顺序略微变化外,其余振型均没有改变。墩身厚度增加或减小16.7%,结构的一阶自振周期相应缩短或延长约5%。墩身截面尺寸的改变对调整结构的自振周期有一定的作用,但不很显著,此时的截面拟定应结合静力状态分析的要求共同考虑。
4 地震响应分析[4]
4.1抗震设防标准及计算参数
本工程主要位于福建省福州市台江区,抗震设防烈度7度区,设计基本地震加速度为0.10g,设计地震分组属第二组,工程场地类别为Ⅲ类,地震动反应谱特征周期值为0.55s。
依据《城市桥梁抗震设计规范》(CJJ 166-2011),本桥抗震设防类别属于丙类。
设计反应谱参数取值如下:
Smax=2.25A
式中,T为结构自振周期,Tg为特征周期,γ为反应谱下降段的衰减指数,阻尼比为0.05时取0.9。η1为自5倍特征周期至6s区段直线下降段下降斜率调整系数,阻尼比为0.05时取0.02,η2为结构的阻尼调整系数,阻尼比为0.05时取1.0。
E1地震作用下:水平向地震动峰值加速度为0.10g,且考虑地震调整系数0.46。E2地震作用下:水平向地震动峰值加速度为0.10g,且考虑地震调整系数2.2。
采用多振型反应谱分析方法对金山大桥主桥分别在E1和E2地震作用下的结构反应进行计算。在反应谱分析中,为保证计算精度,按振型叠加法计算结构最大地震响应时,考虑的振型阶数均在计算方向获得90%以上有效质量,振型组合采用CQC法。
4.2E1、E2地震响应分析
根据《公路桥梁抗震设计细则》(JTG/TB02一01—2008)和《城市桥梁抗震设计规范》(CJJ166—2011),最不利地震响应内力与成桥阶段内力进行组合。由于本桥两个边墩结构一样,高度基本一致,内力差不多;两个主墩墩结构一样,高度基本一致,内力差不多。表4、表5、表6仅示出一个边墩和主墩的验算结果。

表4 桥墩和桩基抗震验算结果(E1地震作用)
注:My为屈服弯矩。
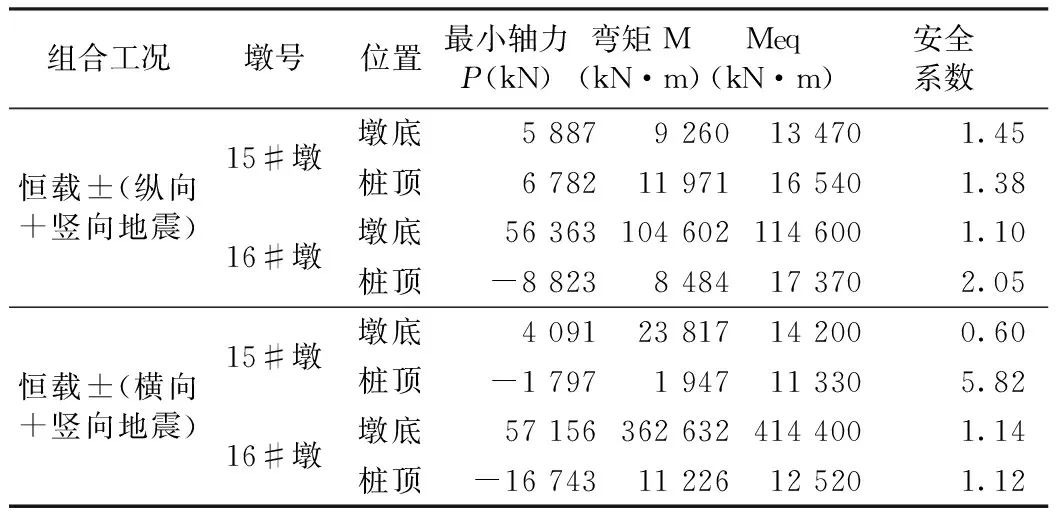
表5 桥墩和桩基抗震验算结果(E2地震作用)
注:Meq为等效屈服弯矩

表6 延性墩墩顶位移验算(E2地震作用,横桥向)
注:Φy为截面屈服曲率,Φu为截面极限曲率,Δd为墩顶位移,Δu为墩顶容许位移

表7 延性墩抗剪强度验算(E2地震作用,横桥向)
综上分析可知:
E1地震作用下,主墩和边墩最不利截面弯矩小于截面初始屈服弯矩,桩基最不利截面弯矩小于截面初始屈服弯矩,满足抗震性能要求。
在E2地震作用下,主墩及其桩基最不利截面弯矩小于截面等效屈服弯矩;边墩及其桩基纵桥向最不利截面弯矩小于截面等效屈服弯矩。边墩横桥向进入延性,墩顶位移小于墩顶容许位移,按能力保护构件验算,边墩横桥向抗剪强度安全系数大于1,均满足抗震性能要求。
5 结论
大跨薄壁矮墩刚构桥的主墩刚度大,体系的前面几阶振型以主梁和边墩的振动为主,主墩参与的振型偏后,改变墩身高度对结构动力特性的影响要比改变墩身厚度的影响明显一些。
在E2地震作用下,本桥的下部结构满足抗震要求。通常都比较重视主墩的抗震设计,但是边墩的受力也是不能忽视,特别是根据各种实际情况,边墩墩形、刚度和主墩有较大区别的情况下,也应做好边墩的抗震设计。
[1]韩丽丽,宁贵霞,侯佳音.高、矮墩连续刚构桥模态与地震响应对比分析[J].中国科技博览,2009(32):113-114.
[2]陈礼榕.大跨矮墩连续刚构地震响应分析[J].四川建筑,2010,6:122-123.
[3]赵旭升.地震响应下矮墩大跨连续刚构桥下部结构受力分析[J].交通世界,2014,7:127-128.
[4]黄国雄.下承式连续梁拱组合式桥梁动力特性与地震响应[D].福州:福州大学,2009.
Dynamic characteristics and seismic response analysis of the short pier continuous rigid frame bridge
HUANGGuoxiong
(Fuzhou Planning Design & Research Institute,Fuzhou 350108)
Taking the main span and hort pier continuous rigid frame bridge of Fuzhou Jinshan double-line bridge as the research object, dynamic characteristics of the short pier continuous rigid frame bridge were calculated and analyzed, Then the influence of lower structural parameters on dynamic characteristics was allso analyzed ,and the bridge seismic response was analyzed by the response spectrum, through the establishment of MIDAS spatial structure model.
Short pier rigid frame; Dynamic characteristics; Seismic response; Parameter analysis
黄国雄(1985.06-),男,工程师。
E-mail:723750679@qq.com
2016-04-29
U443.2
A
1004-6135(2016)06-0092-04

