“一次函数”专家诊疗室
□朱元生
“一次函数”专家诊疗室
□朱元生
今天是“一次函数”专家门诊的日子,这不,主任医师刚上班,就来了好几位慕名而来的患者,下面是几个典型病例诊治情况.
一、对函数图象的意义理解有误
病例1如图1,小明在操场上玩耍,一段时间内沿M→A→B→M的路径匀速散步,能近似刻画小明到出发点M的距离y与时间x之间关系的函数图象是().
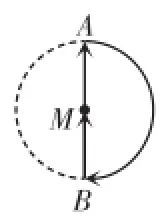
图1
临床症状:选A或B.
病因诊断:这主要是由于对函数图象的意义理解有误,误认为匀速散步,即速度不变,A、B均是半圆,半圆上的点具有到圆心的距离相等的性质,从而误以为应选A或B.题目中要求的是近似刻画小明到出发点M的距离y与时间x之间关系的函数图象,小明在从点M到点A这段时间内,他离点M的距离在逐渐增加,即y随x的增大而增大,图象上升;在从点A到点B这段时间内,小明到点M的距离保持不变,即x增大而y值不变,这时图象应与x轴平行;在从点B到点M的这段时间内,他离点M的距离在逐渐减少,即y随x的增大而减小,图象下降;且从行走的路程上考虑,半圆周长AB要大于直径AB,所以D也不正确.
处方:选C.
二、实际问题中自变量的取值范围的确定欠全面
病例2已知等腰三角形的周长为8cm,写出底边长y(cm)与腰长x(cm)之间的函数关系式,并画出函数图象.
临床症状:底边长y(cm)与腰长x(cm)之间的函数关系式为y= 8-2x,其函数图象如图2所示.
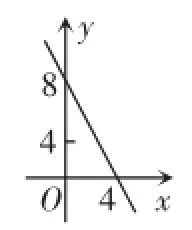
图2
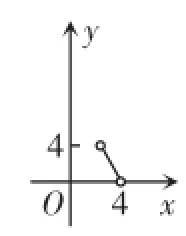
图3
病因诊断:实际问题中自变量的取值范围的确定欠全面.本题既应考虑到腰长x>0,底边长y>0,还应考虑到三角形三边之间的关系,即2x>y,解得2<x<4.
处方:函数关系式为y=8-2x(2<x<4),其函数图象应是如图3所示的不包括端点的一条线段.
三、对一次函数定义的理解出错
病例3已知函数y=(m2-3m)xm2-8+5是关于x的一次函数,试求m的值
临床症状:当m2-8=1时,函数y=(m2-3m)xm2-8+5是一次函数,这时m=±3.
病因诊断:一次函数y=kx+b的定义,不仅要求自变量x的指数为1,同时还要求比例系数即自变量x的系数k≠0,现只考虑到了指数m2-8=1,而遗漏了比例系数m2-3m≠0,事实上,当m=3时m2-3m= 0,这时y=(m2-3m)xm2-8+5就不是一个一次函数.
处方:当函数y=(m2-3m)xm2-8+5是一次函数时,m=-3.
四、忽视分类讨论
病例4:当a为何值时,函数y=(a+1)xa2-3+(a-3)x+a是关于x的一次函数?
临床症状:由题意得,a+1=0且a-3≠0,解得a=-1.
病因诊断:这是由于受思维定势的影响,考虑问题欠周密,忽视了分类讨论.
事实上当a2-3=1且(a+1)+(a-3)≠0,以及当a2-3=0且a-3≠0时,都是一次函数.
处方:(1)当a+1=0且a-3≠0时,解得a=-1;
(2)当a2-3=1且(a+1)+(a-3)≠0时,解得a=±2;
(3)当a2-3=0且a-3≠0时,解得a=
五、对一次函数图象的理解有误
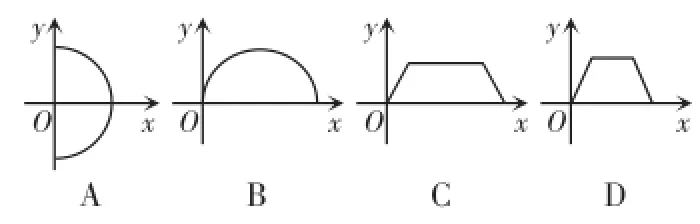
病例5已知函数y=(m-1)x+(3-2m),y随x的增大而减小,则函数的图象大致是下图中的().

临床症状:选A或C
病因诊断:这是由于对一次函数图象的理解有误造成的.以为函数y=kx+b,y随x的增大而减小,即直线下降,忽视了直线与y轴的交点位置.事实上,函数y=kx+b,y随x的增大而减小,则需k<0.即m-1<0,解得m<1,而当m<1时,3-2m>0,即直线与y轴的交点在x轴的上方.
处方:选A.

