一次函数中的相遇与追及
□高 峰
一次函数中的相遇与追及
□高峰
一次函数图象信息题中,有一类相遇或追及的“双线图”问题,由于这类问题的情景比较复杂,图象信息丰富,许多同学在解答这类问题时,感觉十分棘手,下面举例说明此类问题的求解方法.
例1甲、乙两地之间有一条笔直的公路l,小明从甲地出发沿公路l步行前往乙地,同时小亮从乙地出发沿公路l骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.
(1)求小亮从乙地到甲地过程中y2(米)与x(分钟)之间的函数关系式;
(2)求小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
(3)在图2中,补全整个过程中s(米)与x(分钟)之间的函数图象,并确定a的值.

图1

图2
分析:本题涉及的过程比较复杂,我们可以从以下几个方面进行分析.
一、将实际情景与图象结合,把图象分段并与实际情景对应.
根据题意可知小亮与甲地的距离对应的图象是AB、BE、ED、DC,小明与甲地的距离对应的图象是OC.
我们可以把图象分为四段进行分析,如图1,用虚线BG、EF、MN进行分割,从左向右,第一段为小亮到甲地的过程,第二段为小亮到达甲地停留一段时间,第三段为小亮从甲地返回追上小明的过程,第四段为两人一起走的过程.
二、将一次函数中的自变量、函数、系数与实际情景中的数量进行对应,尝试根据已知数量求一些特殊点的坐标或根据坐标求相关数量.
本题自变量表示时间、函数表示距离、而一次函数中自变量系数的绝对值则是速度,本题已经给出了相关点的坐标,可以根据点的坐标求出相关的时间、距离和速度.
由图象可得C(40,2000)、A(0,2000)、B(10,0),根据C(40,2000)可得小明的速度为2000÷40=50米/分,根据A(0,2000)、B(10,0)小亮的速度为2000÷10=200米/分.
三、尝试求出相关图象的函数关系式,利用函数关系式解决问题.
(1)根据小亮从乙地到甲地过程对应的图象是AB,可设小亮从乙地到甲地过程中y2(米)与x(分钟)之间的函数关系式为y2=kx+b,将A(0,2000)、B(10,0)代入,可得k= -200,b=2000,所以y2=-200x+ 2000.
(2)从图象上可以看出,小亮从甲地返回到与小明相遇的过程是第三段,所以只需求出DE和OC的对应函数关系式作差即可.
小亮从甲地返回追小明的过程对应的图象是DE,设yDE=kx+b,根据小亮的速度为200米/分,由匀速直线运动中斜率即表示速度,可知k=200,又有点E(24,0),即可求出b=-4800,于是yDE=200x-4800,而根据图象可求出yOC=50x,
所以小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式为s=50x-(200x-4800)=-150x+4800.
(3)补全整个过程中s(米)与x(分钟)之间的函数图象,需要把第一段再分为两部分,即第一次相遇前和第一次相遇后,所以图2可分为五段考虑.
第1段(AG段中相遇前):显然a表示小亮从乙地出发与小明从甲地出发第一次相遇的时间,根据(2)求出的速度,可得a=2000÷(200+ 50)=8分钟,本段对应的时间为0≤x≤8;
第2段(AG段中相遇后):相遇后到小亮到甲地,这段时间是2分钟,总时间是10分钟,当x=10时,s=2×(50+200)=500,本段对应的时间是8≤x≤10;
第3段(GF段):小亮到甲地后休息了14分钟,总时间是24分钟,相距的距离是小明走的路程,当x= 24时,s=24×50=1200,本段对应的时间是10≤x≤24;
第4段(FM段):小亮到甲地休息完到追上小明,这时s=0,代入s=-150x+4800,可求得x=32,本段对应的时间是24≤x≤32;
第5段(MC段):这时s都为0,本段对应的时间是32≤x≤40.
根据以上信息可描出相应的点就可以补全图象,如图3.
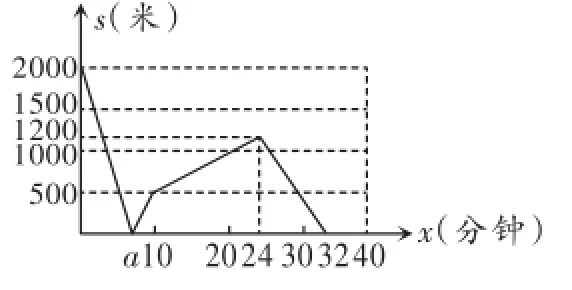
图3
点评:本题的难点就是过程比较复杂,解决问题时首先将过程进行分段,将每段与对应的图象结合起来,既要充分利用隐含在图象中的信息,也要挖掘隐含在题目文字中的信息,特别是相关数量之间的关系.对于最后的补图,关键是确定好段与段的“界点”的坐标.
例2(2015·金华)小慧和小聪沿图4中的景区公路游览.小慧乘坐车速为30km/h的电动汽车,早上7:00从宾馆出发,游玩后中午12:00回到宾馆.小聪骑车从飞瀑出发前往宾馆,速度为20km/h,途中遇见小慧时,小慧恰好游完一景点后乘车前往下一景点.上午10:00小聪到达宾馆.图5中的图象分别表示两人离宾馆的路程s(km)与时间t(h)的函数关系.试结合图中信息回答:
(1)小聪上午几点钟从飞瀑出发?
(2)试求线段AB、GH的交点B的坐标,并说明它的实际意义.
(3)如果小聪到达宾馆后,立即以30km/h的速度按原路返回,那么返回途中他几点钟遇见小慧?
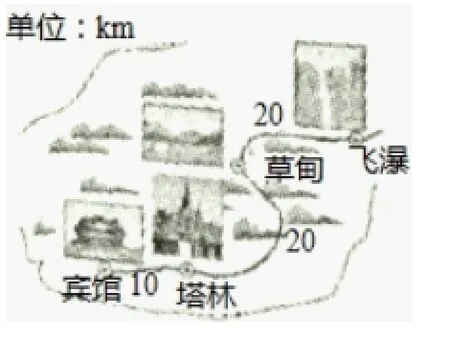
图4
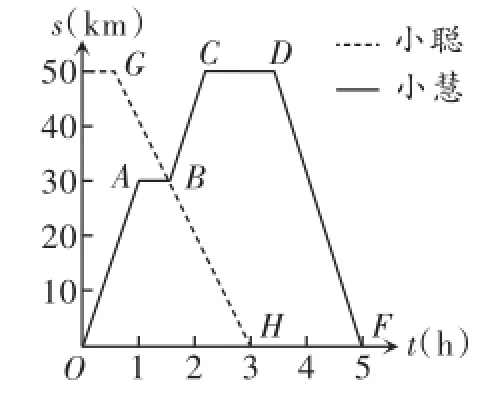
图5
分析:(1)求出小聪从飞瀑到宾馆所用的时间即可求得小聪上午从飞瀑出发的时间.
(2)应用待定系数法求出直线GH的函数表达式,即可由点B的纵坐标求出横坐标而得点B的坐标;点B的实际意义是:上午8∶30小慧与小聪在离宾馆30km(即景点草甸)处第一次相遇.
(3)求出直线DF和小聪返回时s关于t的函数(HM),二者联立即可求解.
解:(1)小聪骑车从飞瀑出发到宾馆所用时间为50÷20=2.5(小时),
因为上午10:00小聪到达宾馆,
故小聪上午7点30分从飞瀑出发.
(2)3-2.5=0.5,
则点G的坐标为(0.5,50).
设GH的解析式为s=kt+b,
把G(0.5,50)、H(3,0)代入,
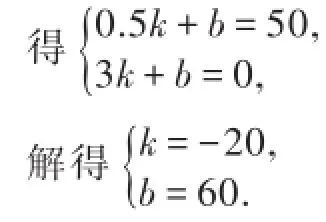
故s=-20t+60.
当s=30时,t=1.5,
B点的坐标为(1.5,30).
点B的实际意义是:当小慧出发1.5小时时,小慧与小聪相遇,且离宾馆的路程为30km.
(3)设直线DF为s=k1t+b1,
因为小慧回到宾馆的速度是30km/h,所以k1=-30,
又该直线过点F(5,0),可得b1=150,
∴直线DF的函数表达式为s=-30t+150.
如图6,HM为小聪返回时的函数图象.设直线HM为s=k2t+b2,因为小聪上午10:00到达宾馆后立即以30km/h的速度返回飞瀑,所以k2=30,该直线过点H(3,0),可得b2=-90,
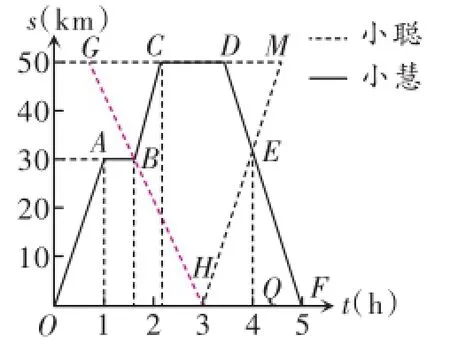
图6
故直线HM的函数表达式为s= 30t-90.
由-30t+150=30t-90解得t=4,对应时刻7+4=11,
∴小聪返回途中上午11:00遇见小慧.
点评:解决问题的关键是将每段图象与实际情景对应,将特殊点的坐标与实际情景中的量对应,利用数量之间的关系求出点的坐标,从而求出对应的关系式,然后利用关系式求解.

