核主成分分析在地球化学元素组合异常圈定中的应用
黄志强, 任鸿飞, 梁芳敏, 魏继祖, 段长生
(1.河南省有色金属地质矿产局 第六地质大队,郑州 450000;2.成都理工大学 地球物理学院,成都 610059; 3.赣中南地质矿产勘查研究院,南昌 330000)
核主成分分析在地球化学元素组合异常圈定中的应用
黄志强1, 任鸿飞1, 梁芳敏1, 魏继祖1, 段长生2,3*
(1.河南省有色金属地质矿产局第六地质大队,郑州450000;2.成都理工大学地球物理学院,成都610059; 3.赣中南地质矿产勘查研究院,南昌330000)
地球化学元素作为成矿预测一种重要的数据源,其异常分析往往是进行下一步找矿工作的基础,也是确定找矿靶区一种重要技术手段。作者以青海省大柴旦镇柴达木山南坡一带为研究区,通过开展1:10 000土壤地球化学测量,共分析了Au、Cu、Pb、Zn、As、Sb六种元素,采用核主成分分析地球化学元素组合异常,并与主成分分析进行比较分析,从应用结果可以看出核主成分的降维效果更好。从异常等值线图可以看出,采用核主成分的异常区域分布更加集中,所圈定的元素组合异常与已知矿床点在空间上具有良好的对应关系,说明利用核主成分圈定元素组合异常能够较好地确认地球化学元素组合异常。
核主成分分析; 主成分分析; 异常圈定; 地球化学
0 引言
如何准确有效地开展成矿预测是近年来研究者的焦点。尽管化探元素异常信息的筛选和评价为找矿提供了可靠的依据,但由于单一元素异常信息的评价对找矿仍存在不确定性,因而需要考虑多元素组合异常对找矿的贡献作用[1]。元素组合异常考虑了研究区域上与成矿因素相关的多种元素信息,同时又考虑了元素间的相互关系,这说明元素组合异常能够充分地反映研究区域元素异常信息的总体分布特征和成矿的地质特征。更重要的是,研究元素的共生组合有助于了解地质体的成因条件,因此具有重要的找矿意义[2]。
主成分分析是处理数据降维的重要方法,但该方法针对非线性的数据问题分析效果并不是很好,而化探元素本质上存在非线性关系,仅靠线性的提取方法并不能提取到最优的成分信息,甚至会降低模型的精度。考虑采用改进的主成分分析即核主成分分析方法,通过引进核函数更好地对数据进行预处理[3]。目前核主成分分析方法在许多研究领域都取得了大量研究成果,庞河清等[3]通过核主成分分析与支持向量机相结合,实现了储层识别;葛新民等[4]运用核主成分分析与小波能谱分析对复杂储层油水界面进行了预测;肖慧等[5]在神经网络集合基础上运用核主成分对台风进行建模研究;陈斌等[6]基于核主成分提出一种关于时间域航空电磁去噪的方法等。
这里以青海省大柴旦镇柴达木山南坡一带为例,采用核主成分分析对地球化学元素数据进行分析处理,进而求取地球化学元素组合异常,并与主成分分析进行对比研究。
1 研究区土壤地球化学元素特征
以青海省大柴旦镇柴达木山南坡一带为研究区域[7],通过开展1∶10 000土壤地球化学测量,共分析了Cu、Au、Zn、As、Sb、Pb六种土壤地球化学元素,得到3 307个样本数据。数据集的基本的特征参数见表1。
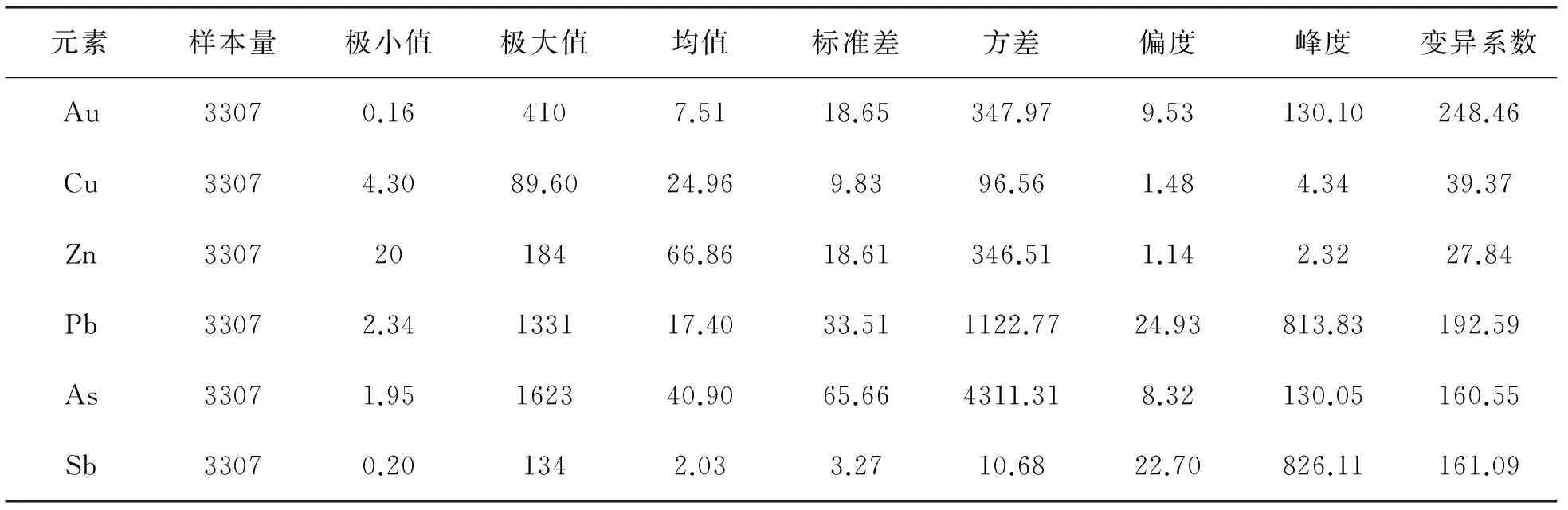
表1 研究区Au、Cu、Zn、Pb、As、Sb六种土壤地球化学元素特征参数表
2 主成分分析
2.1基本原理
主成分分析(Principal Component Analysis, PCA)最初由Karl Parson针对非随机变量提出,其主要目的是通过降维得到具有综合性特征且彼此独立的少量属性变量(即主成分,又称主分量)。主成分分析方法是目前最常用的属性降维方法,其将原始属性变量进行线性表示从而得出综合属性变量,所以从本质上说主成分分析方法是一种处理属性之间线性关系的方法,但是当面临属性间非线性问题的时候得不到理想的效果。主成分分析方法究其本质,还是对特征向量进行线性变换[8]。
2.2主成分分析
通过计算得到的第一主成分和第二主成分分别为:F1=-0.108×Au+0.922×Cu+0.456×Pb+
0.859×Zn-0.118×As+0.301×Sb
F2=0.753×Au-0.13×Cu+0.357×Pb-
0.207×Zn+0.691×As+0.347×Sb
通过前两个主成分可以发现,第一主成分中Cu、Pb、Zn的系数分别为0.922、0.456和0.859,说明这3种元素对于第一主成分具有较强的正载荷,而Au、As对第一主成分具有比较弱的负载荷;第二主成分中系数最高的是Au(0.753)、Pb(0.357)、Sb(0.347)和As(0.691),说明这4种元素对于第二主成分具有中强程度的正载荷,所以第一主成份主要反映了Cu-Pb-Zn元素的综合指标,第二主成份主要反映了Au-Pb-Sb-As元素的综合指标。
计算得到特征值和各个特征值对应的累计贡献率,如表2所示。从表2中可见,前2个特征值所对应的累计贡献率为54.37%,前3个特征值所对应的累计贡献率也只有70.86%,远没有达到85%。这就是说如果提取前2个主成分,丢失的信息占原始信息的45.63%。
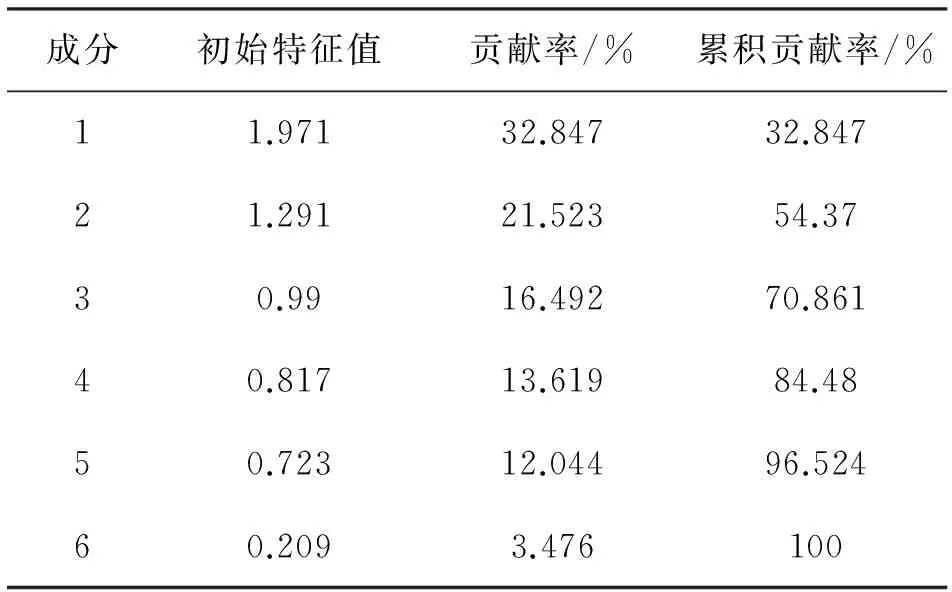
表2 主成分分析特征值、贡献率和累计贡献率
3 核主成分分析
3.1核函数
核函数在处理非线性问题以及维数灾难的问题方面非常有效。目前常用的核函数主要有多项式核函数、高斯核函数、动态核函数、Sigmoid核函数、神经网络核函数等,其计算公式分别为:
1)多项式核函数:
(1)
2)高斯核函数[9]:
(2)
3)Sigmoid核函数[10]:
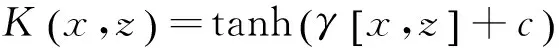
(3)
4)神经网络核函数[6]:
(4)
其中:s、t、p、σ、γ和c均为实常数。
3.2核主成分分析
核主成分分析(Kernel Principal Component Analysis, KPCA)是在主成分分析(PCA)基础上,进行推广的一种非线性特征提取方法。其基本思想是把输入的数据通过非线性映射从输入空间变换到高维特征空间(即再生核希尔伯特空间),然后再在特征空间中进行主成分分析,在计算点内积时采用核函数代替内积运算,从而实现非线性特征的提取[11,12]。核主成分分析中采用核函数是分析的关键,其不需要知道非线性映射的具体变换形式,在进行非线性变换之后,通过用原始空间的核函数计算代替特征空间的内积运算,极大程度上减少了计算量,同时能提供比主成分分析更多的非线性信息[13]。
核主成分的计算步骤[8]为:
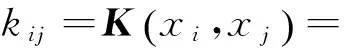
(5)
其中:i,j=1,2,…,l;K满足Mercer定理。
3)将核矩阵进行修正[14],使其中心化:
K′=K-IK-KI+IKI
(6)
4)计算核矩阵K′/l的特征值(λ1,λ2,…,λl),以及特征值所对应的特征向量(v1,v2,…,vl)。
5)用斯密特正交法对特征向量(v1,v2,…,vl),进行正交化得正交特征向量:(α1,α2,…,αl)。
6) 此时样本x的核主成分的结果为:
(7)
其中j=1、2、…、l、λk为第k个主成分的特征值。
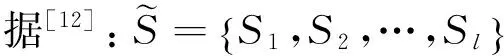
3.3基于核主成分的元素组合异常分析
选取多项式核函数
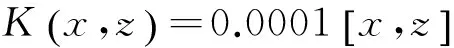
(8)
进行核主成分分析,计算得到核主成分特征值、贡献率和累计贡献率结果如表3所示。
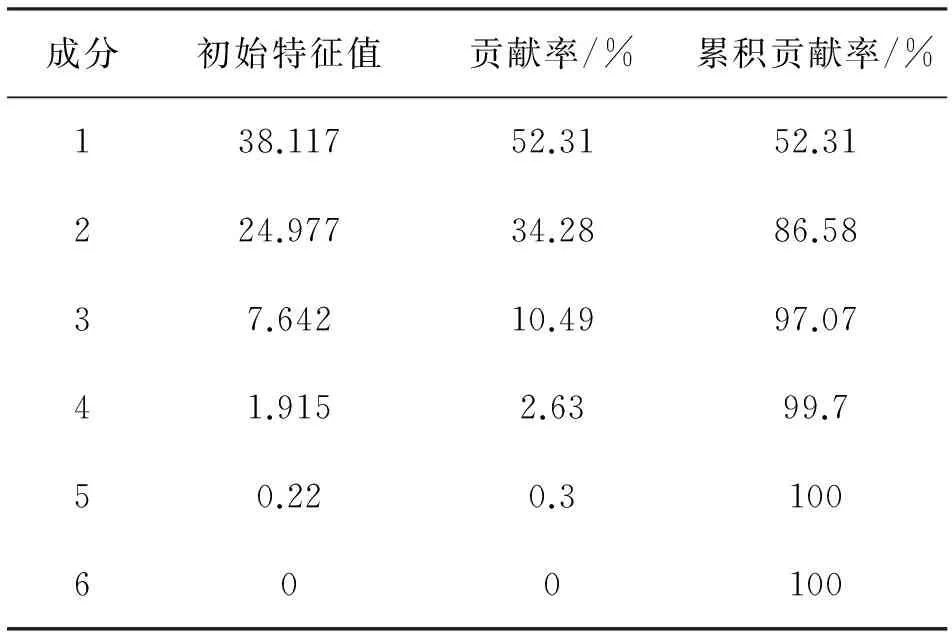
表3 核主成分分析特征值、贡献率和累计贡献率
由表3可知,第一主成分的贡献率达到52.31%,前两个主成分的累计贡献率为86.58%,涵盖了数据的大部分信息量,降维效果明显。利用式(7)计算出核主成分,如表4所示。
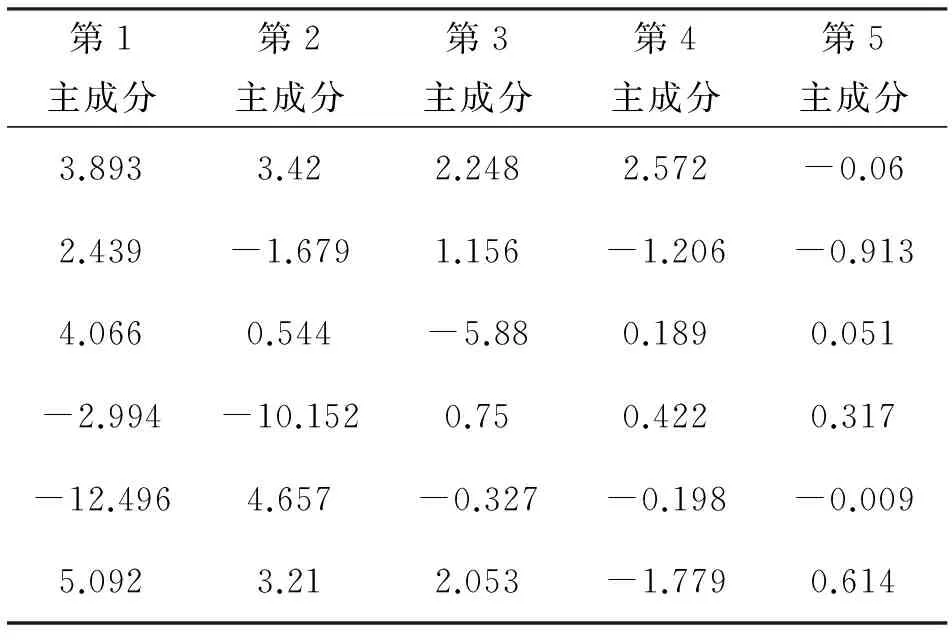
表4 核主成分分析结果
3.4核主成分与主成分的对比分析
将核主成分和主成分的综合变量的平均值加n倍标准差来确定化探数据异常分带序列,生成化学元素组合异常等值线图(图1~图2)。对比核主成分与主成份分析的异常区域可以看出,核主成分的异常区域分布更加集中。这对指导找矿提供了更加科学的依据,提高了找矿效率,圈定的异常在后期工作中有较好的发现,因此,利用核主成分分析方法对于优选成矿具有更好的效果。
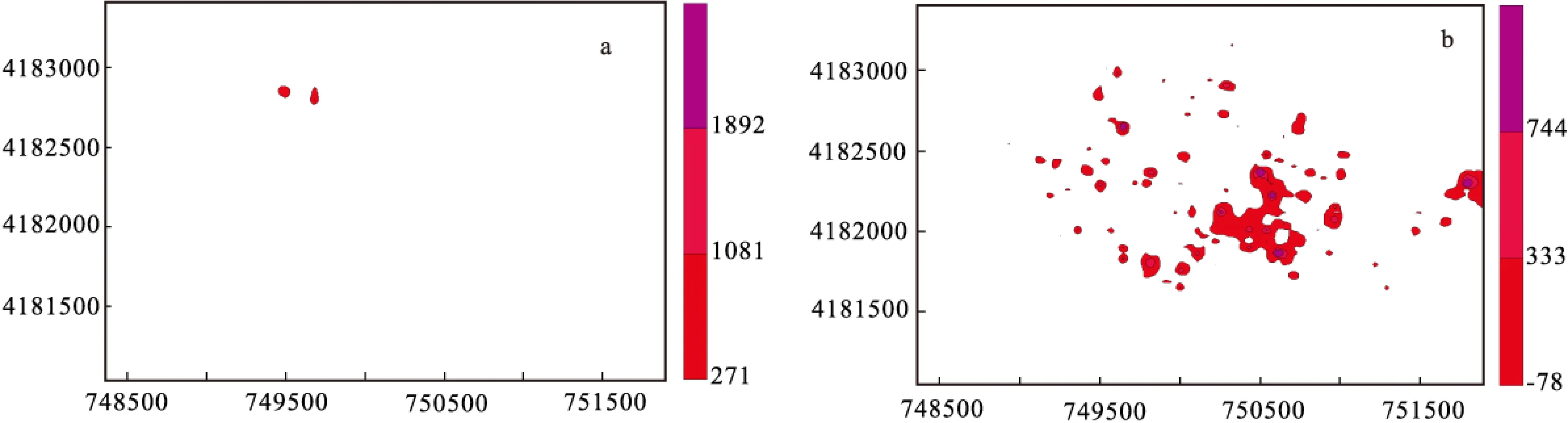
图1 核主成分元素组合异常等值线图Fig.1 Element combination anomaly contour maps generated by kernel principal component analysis(a) 第一主成分;(b) 第二主成分
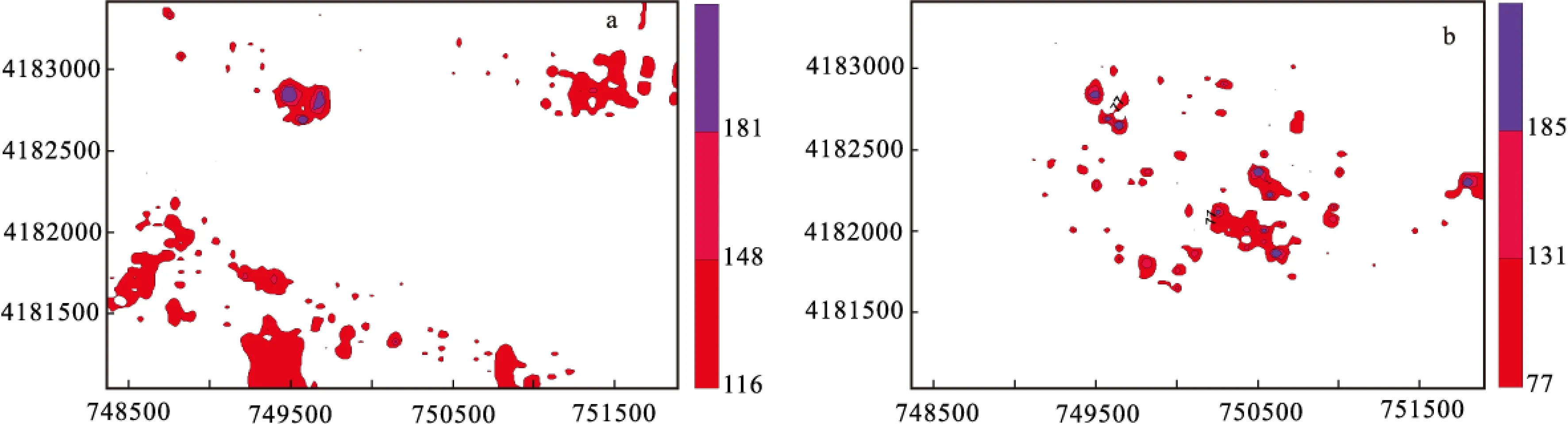
图2 主成分元素组合异常等值线图Fig.2 Element combination anomaly contour maps generated by principal component analysis(a) 第一主成分;(b) 第二主成分
4 结 论
通过核主成分分析对青海省大柴旦的化探元素数据进行分析,将核主成分分析结果与主成分分析结果进行对比分析,得出以下结论:
1)核主成分分析前两个主成分累计贡献率高达86.58%,而主成分分析前两个主成分累计贡献率只有54.37%,核主成分的降维效果相对较好。
2)核主成分分析在主成分分析的基础之上,考虑数据的非线性信息,获得数据的高阶特征,相比主成分分析能够获取更充分的信息,同时,从核主成分元素组合异常等值线图可以看出,核主成分析圈定的异常区域分布更加集中,更能凸显地球化学元素的异常分布,所圈定的异常区域与后期实际工程验证结果吻合,说明核主成分分析在圈定元素组合异常方面能取得更好的效果。
[1]于林松,邱成贵,刘伟. 青海省北部绿草山地区化探元素组合分类信息探讨[J]. 山东国土资源, 2014, 30(02): 50-53.
YU L S, QIU C G, LIU W. Discussion on Geochemical Elements Classifing Information in Lvcaoshan Mountain in North of Qinghai Province[J]. ShangDong Land and Resources, 2014, 30(02): 50-53.(In Chinese)
[2]刘桂阁,李艳秋,常春郊,等. 区域化探数据处理的综合异常法研究[J]. 黄金科学技术, 2012, 20 (04): 67-69.
LIU G G, LI Y Q, CHANG C J, et al. Research on Comprehensive Anomaly Method of Regional Geochemical Exploration Data Processing[J]. Gold Science and Technology, 2012, 20 (04): 67-69(In Chinese)
[3]庞河清,匡建超,王众,等. 核主成分分析与支持向量机模型在储层识别中的应用[J]. 物探与化探,2012,(36)6:1001-1005.
PANG H Q,KUANG J C, WANG Z, et al.The Application Of a KPCA-AVM Model To Reservoir Indentification [J]. Geophysical and Geochemical Exploration, 2012, (36)6: 1001- 1005. (In Chinese)
[4]葛新民,范卓颖,范宜仁,等. 基于核主成分—小波能谱分析的复杂储层油水界面预测[J]. 中南大学学报,2015,(46)5:1747-1753.
GE X M, FAN Z Y, FAN Y R, et al. Oil/water contact prediction of complex reservoir using kernel principal component analysis and wavelet power spectrum analysis[J]. Journal of Central South University, 2015,(46)5:1747-1753. (In Chinese)
[5]肖慧,刘苏东,黄小燕,等. 基于核主成分的神经网络集合预报建模研究[J]. 计算机仿真,2010,27(12):163-166.
XIAO H, LIU S D, HUANG X Y, et al. A study on neural network ensemble forecast model based on kernel principal component Analysis[J]. Computer simulation, 2010,27(12):163-166. (In Chinese)
[6]陈斌,陆从德,刘光鼎. 基于核主成分分析的时间域航空电磁去噪方法[J].地球物理学报,2014,57(1):295-302.
CHEN B, LU C D, LIU G D. A denoising method based on kernel principal component analysis for airborne time domain electromagnetic data[J]. Chinese Journal of Geophysics, 2014,57(1):295-302. (In Chinese)
[7]徐彬. 金铜矿化探数据分析及成矿预测研究[D].成都:成都理工大学,2014.
XU B. Data processing in geochemical exploration and metallogenic prognosis of gold and copper ore: with the northern margin of the Qaidam Basin Qaidam Mountain Chaoliben Tavan Tolgoi area as an example [D].Chengdu:Chengdu University of Technology,2014. (In Chinese)
[8]李洁. 基于核主成分降维的RBF网络降水预测[J]. 柳州师专学报, 2012,27(1):111-117.
LI J. On RBF Network Precipitation Forecast Based on Kernel Principal Component Dimension Reduction[J]. Journal of Liuzhou Teachers College, 2012,27(1):111-117. (In Chinese)
[9]杨道军,钱新,钱瑜,等. 核主成分分析法在生态经济可持续发展评价中应用[J]. 环境科学与技术,2007,12:91-93+122.
YANG D J, QIAN X, QIAN Y, et al.. Application of Kernel Principal Component Analysis in Evaluation of Sustainable Development of Ecological Economy[J]. Environmental Science & Technology, 2007,12:91-93+122. (In Chinese)
[10]吴今培. 基于核函数的主成分分析及应用[J]. 系统工程, 2005, (23) 2: 117-120.
WU J P . Principle component analysis and application based on kernel function[J]. systems engineering, 2005, (23) 2: 117-120. (In Chinese)
[11]向小东,宋芳. 基于核主成分与加权支持向量机的福建省城镇登记失业率预测[J].系统工程理论与实践,2009,(29)1:73-80.
XIANG X D, SONG F. Forecasting of the urban registered unemployment rate in Fujian province based on kernel principal component analysis and weighted support vector machine[J]. Systems Engineering -Theory & Practice, 2009,(29)1:73-80. (In Chinese)
[12]郭秀峰,任贺宇.基于核主成分分析和RVM的传感器故障诊断算法设计[J]. 自动化测试技术, 2014,22(3) :709-712.
GUO X F, REN H Y. Design of Fault Diagnosis Algorithm for Sensor Node Based on Kernel Principal Component Analysis and RVM[J]. Computer Measurement & Control, 2014,22(3) :709-712. (In Chinese)
[13]韦振中. 基于核主成分分析的特征提取方法[J]. 广西工学院学报,2006, (17)4:27-31.
WEI Z Z. Feature extraction based on Kernel Principal Component Analysis[J]. Journal of Guangxi University of Technology, 2006, (17)4:27-31. (In Chinese)
[14]徐义田,王来生,崔文善,等. 核主成分分析(KPCA)在企业经济效益评价中的应用[J]. 数学的实践与认识,2006(01):35-38.
XU Y T, WANG L S, CUI W S,et al. Application of the Kernel Principal Component Analysis in Comprehensive Evaluation of Enterprise Economic Results[J]. Mathematics in Practice and Theory, 2006(01):35-38. (In Chinese)
The application of kernel principal component analysis to the anomaly delineation of geochemistry element association
HUANG Zhi-qiang1, REN Hong-fei1, LIANG Fang-min1, WEI Ji-zu1,DUAN Chang-sheng*2,3
(1.Geological brigade 6 in Bureau of geology and mineral resources of nonferrous metal ,Henan province471002,China;2.Chengdu University of Technology,Chengdu610059,China;3.Institute of Geological and Mineral Exploration in central and south Jiangxi Province,Nanchang330029,China)
Geochemical element as an important data source of metallogenic prediction, the abnormal analysis is often the basis for the next step prospecting work, and is an important technical means to confirm prospecting targets. In this paper , taking Qinghai province Dachaidan town along the southern slope of the Chaidamu mountain area as the research region, carried out by 1: 10000 soil geochemical measure to analysis a total of Au, Cu, Pb, Zn, As, Sb six elements, and using kernel principal component to analysis geochemical anomalous element assemblage, and then compared with principal component analysis. Results can be seen from the application that the dimension reduction effect of kernel principal component is better than principal component analysis. Besides, from the unusual contour map it can be shown that the distribution of abnormal area is more concentrated by using kernel principal component analysis, and Element combination anomalies of delineation is with good correspondence between the space of known deposits. It declare that kernel principal component delineate abnormal combination of elements can be better recognized geochemical element combination anomalies .
principal component analysis; kernel principal component analysis; anomaly delineation; geochemistry
2016-05-20改回日期:2016-06-08
中国地质调查局地质矿产调查评价专项(资[2014] 01-015-018);国家高技术研究发展计划(863计划)项目(2009AA06Z108)
黄志强(1971-),男,硕士,高级工程师,主要从事水文地质及岩土工程, E-mail:835104143@qq.com。
段长生(1974-),男,博士,主要从事电磁法正演模拟和反演成像,E-mail:49119428@qq.com。
1001-1749(2016)04-0560-06
P 595
A
10.3969/j.issn.1001-1749.2016.04.19

