区间直觉模糊数密度加权算子及其决策应用

杜迎雪, 常　娟, 刘卫锋

(郑州航空工业管理学院 理学院，河南 郑州 450015)



区间直觉模糊数密度加权算子及其决策应用

杜迎雪, 常娟, 刘卫锋

(郑州航空工业管理学院 理学院，河南 郑州 450015)

在多属性决策中，当属性值为区间值直觉模糊数时，考虑属性信息分布疏密程度，研究了区间值直觉模糊集数据聚类的问题，提出了新的算子——线性区间值直觉模糊数密度加权平均中间算子(IIFDWA)和积性区间值直觉模糊数密度加权平均中间算子(IIFDWGA)，统称区间值直觉模糊密度加权算子.最后,将IIFDWA算子和WAA算子结合应用到多属性群决策问题中.

多属性决策；区间直觉模糊数；区间直觉模糊数密度加权算子；聚类

多属性决策是现代决策理论的重要组成部分，它在工程设计、经济管理、军事等诸多领域有着广泛的应用.信息集成算子是多属性决策研究的一个核心问题，许多学者对其进行了深入研究.Yager[1]于1988年提出了有序加权平均(OWA)算子；Chiclana等[2]和Xu等[3]将OWA算子进行推广，提出了有序加权几何平均(OWGA)算子；陈华友等[4]提出了有序加权调和平均(OWHA)算子.但是，这些集成算子没有考虑属性值分布的疏密程度.在多属性决策中，属性值分布是不均匀的，所以关注数据疏密程度的信息非常必要.为此，易平涛等[5-11]提出了实点型密度算子、区间数密度算子、三角模糊数密度算子、直觉模糊密度算子、语言信息密度算子等其他密度算子,并将这些算子与AA算子、WAA算子、OWA算子、Min算子、Max算子等结合，应用到多属性决策中并取得了更好的决策结果.

在上述研究的基础上，继续研究区间直觉模糊数集的数据聚类问题，并提出了一种简单且有效的聚类方法.然后，提出了线性区间值直觉模糊数密度加权平均算子和积性区间值直觉模糊数密度加权平均算子，统称区间值直觉模糊密度加权算子.将线性区间值直觉模糊数密度加权平均算子和WAA算子结合，得到了一种信息集结算子——线性区间直觉模糊数密度加权算数平均算子 (IIFDWA).最后,将该算子应用在多属性群决策中.

1　预备知识

定义1[12]设X为给定论域，则X上的区间值模糊集是一个映射X→Int([0,1])，这里Int([0,1])代表[0,1]上所有闭子区间的集合.

论域X上所有区间值直觉模糊集记作IVFS(X).

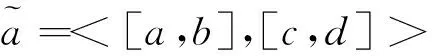
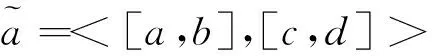
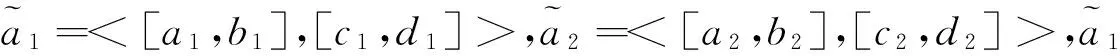
下面将区间直觉模糊集的隶属度期望值和可能度进行聚类.

2　区间值直觉模糊数的聚类

步骤(1)：令计数器r=0，A′=A.

步骤(3)：令r=r+1，A′=A′-Cr-1，若A′=φ，则聚类结束，否则转入步骤(2).

3　密度加权向量

密度权重反映了决策者对各组信息规模的偏好程度.文献[6]、[8]和[9]通过主观赋权法或主客观相结合的方法来确定密度权重，下面提出一种密度权重客观赋权方法.

按照元素个数从多到少的顺序对A1,A2,…,Al进行降序排列，得到序化后的聚类组.为了方便，仍记为A1,A2,…,Al，各组元素个数满足kj≥kj+1(j=1,2,…,l).

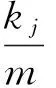
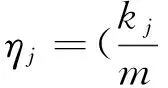
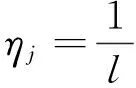
4　区间直觉模糊数密度算子

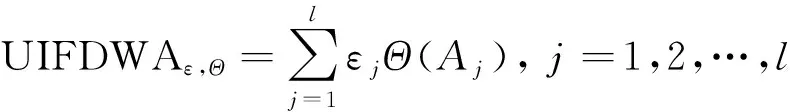
则称UIFDWA为线性区间直觉模糊数密度加权平均中间算子，也称为IIFDWA算子.若

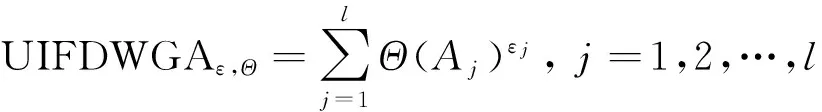
则称UIFDWGA为积性区间直觉模糊数密度加权平均中间算子，也称为IIFDWGA算子.

其中，密度加权向量为ε=(ε1,ε2,…,εl)T，Θ(Aj)为已有的信息集结算子.将UIFDWA算子和IIFDWGA算子统称为区间直觉模糊数的密度算子.

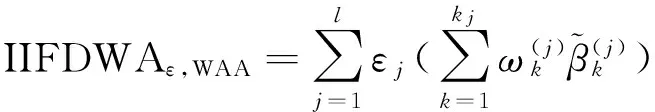
称函数UIFDWAε,WAA为线性区间直觉模糊数密度加权算术平均算子，也称为IIFDWAε,WAA算子.

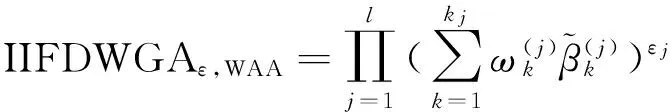
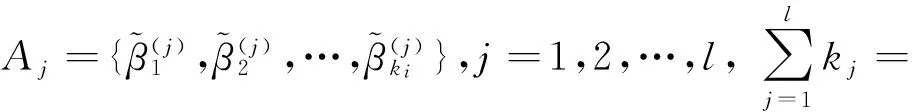
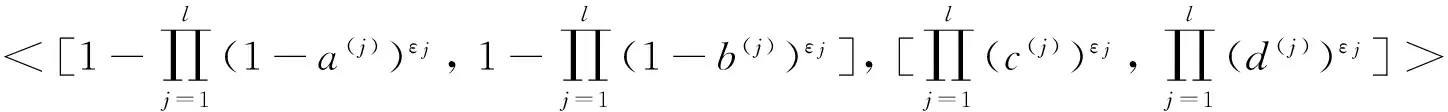
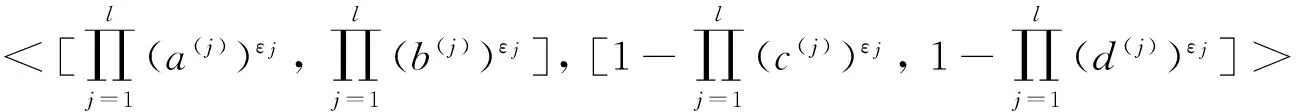
区间直觉模糊数密度中间算子也可以与Max算子、Min算子、OWA算子等合成为新的信息集结算子，这里不一一赘述.

5　决策应用

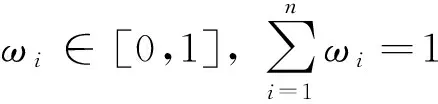
区间值直觉模糊密度算子的多属性决策方法步骤如下：

步骤(1) 将决策矩阵A=(aij)m×n的每一行根据区间值直觉模糊集聚类方法进行聚类；

步骤(3) 利用区间值直觉模糊密度算子对每行进行集结, 得到αi=IIFDM(ai1,ai2,…,am).

步骤(4) 计算每个αi的得分函数值，如果得分函数值s(αi)相等，需要计算精确函数值H(αi)；

步骤(5) 根据得分函数值s(αi)和精确函数值H(αi)的大小进行排序；

例2某单位在对干部进行考核选拔时，首先制定了6项考核指标：思想品德(G1)，工作态度(G2)，工作作风(G3)，文化水平和知识结构(G4)，领导能力(G5)，开拓能力(G6).指标权重向量为ω=(0.2,0.1,0.25,0.1,0.15,0.2)T.然后，由群众推荐并评议，确定了5位候选人.假设每个候选人在各指标下评估信息，经过处理后可表示为区间直觉模糊数，如表1所示.

表1　决策矩阵

(1)根据聚类方法，计算每个区间值直觉模糊数所对应的隶属度期望值和非隶属度期望值，见表2.

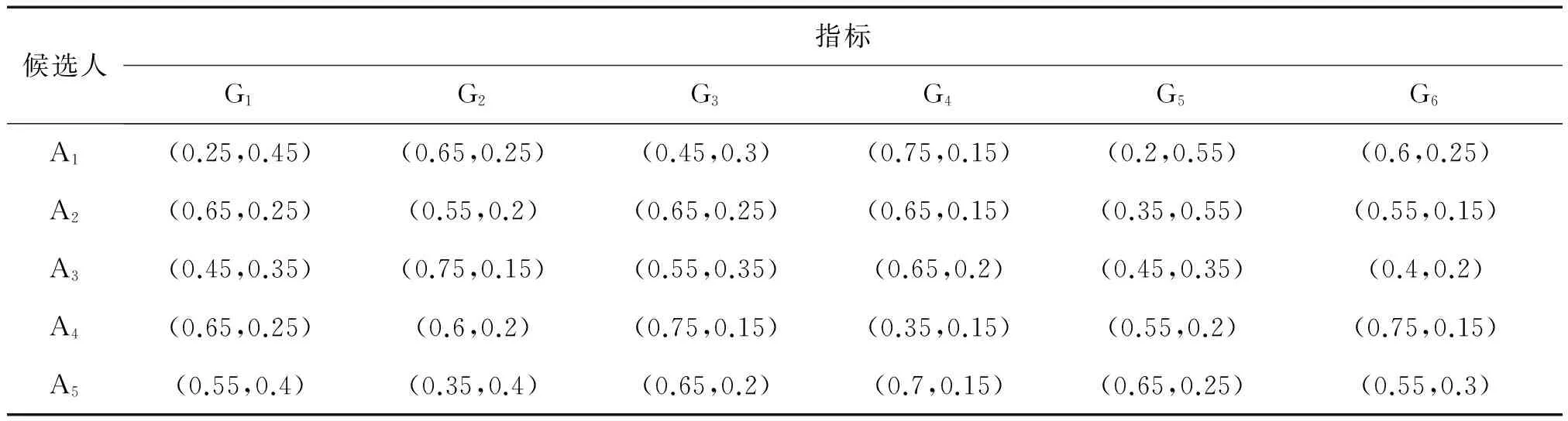
表2　隶属度与非隶属度的期望值

根据上述对进行分类，得到聚类组如下：

A1的分组为 B1={x12,x13,x16}，B2={x11,x15}，B3={x14}，

A2的分组为B1={x21,x22,x23,x24,x26}，B2={x25}，

A3的分组为B1={x31,x33,x35,x36}，B2={x32}，B3={x34}，

A4的分组为B1={x42,x44,x45}，B2={x42,x46}，B3={x41}，

A5的分组为B1={x53,x54,x55}，B2={x51,x56}，B3={x52}，

其中，xij为表1中的区间直觉模糊数.

(2)密度加权向量的确定.

假设决策者对信息没有偏好,求得每个聚类的密度加权向量分别为

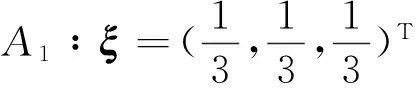
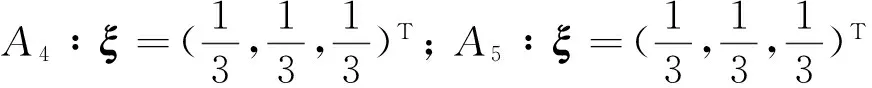
(3)利用区间值直觉模糊密度算子对每行进行集结，得到候选人的综合属性值.

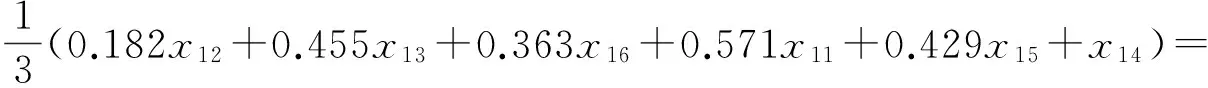
<[0.491 2,0.624 5],[0.206 5,0.333 3]>=α1.

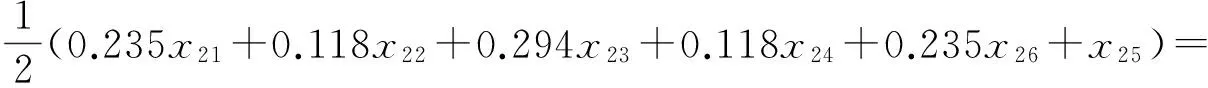
<[0.437 7,0.537 1],[0.268 6,0.395 0]>=α2.

<[0.586 5,0.696 4],[0.131 6,0.281 6]>=α3.

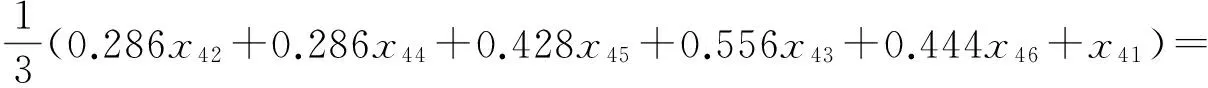
<[0.595 8,0.708 3],[0.126 0,0.252 1]>=α4.

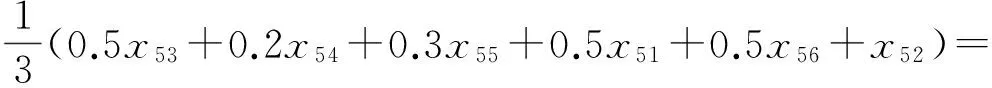
<[0.480 8,0.595 1],[0.208 4,0.395 5]>=α5.

(4)计算每个αi得分函数值,s(α1)=0.288 05,s(α2)=0.155 6,s(α3)=0.434 85,s(α4)=0.463,s(α5)=0.236.

(5)按得分函数值s(αi)的大小进行排序,显然s(α4)>s(α3)>s(α1)>s(α5)>s(α2).

[1]YAGERRR.Onorderedweightedaveragingaggregationoperatorsinmulti-criteriadecisionmaking[J].IEEETransactionsonSystems,ManandCybernetics:partB,1998(18):183-190.

[2]CHICLANAF,HERRERAF,HERRERAE.Theorderedweightedgeometricoperator:propertiesandapplications[C]∥Proceeding8thInternationalConferenceonInformationProcessingandManagementofUncertaintyinKnowledgeBasedSystems:Madrid:[s.n.].2000:985-991.

[3]XUZS,DAQL.Theorderedweightedgeometricaveragingoperator[J].InternationalJournalofIntelligentSystems,2002(17)：709-716.

[4]陈华友，刘春林，盛昭瀚.IOWHA算子及其在组合预测中的应用[J].中国管理科学，2004,12(5):35-40.

[5]易平涛，郭亚军，张丹宁.密度加权平均算子在多属性决策中的应用[J].控制与决策，2007,22(5)：515-519.

[6]易平涛，郭亚军，张丹宁.意见分歧特征下多评价结论协商组合方法[J].东北大学学报(自然科学版)，2006，27(12):1289-1392.

[7]易平涛，郭亚军.多元密度集结算子及其性质分析[J].系统管理学报,2008,17(4):401-408.

[8]易平涛，郭亚军.广义实型密度加权平均中间算子及其应用[J].系统工程学报,2010,25(2):190-195.

[9]易平涛，高立群，郭亚军.基于多元密度集结算子的组合评价方法[J].系统工程与电子技术，2009，31(12):2882-2887.

[10]易平涛，李伟伟，郭亚军,等.诱导密度算子及其性质分析[J].系统管理学报，2011，20(5):527-532.

[11]易平涛.多元信息密度集结算子理论及应用[M].北京：科学出版社，2012.

[12]张小红，裴道武，代建华.模糊数学与Rough集理论[M].北京：清华大学出版社，2013.

[13]LIUXW,CHENLH.OnthepropertiesofparametricgeometricOWAoperator[J].InternationalJournalofApproximateReasoning,2004(35)：163-178.

[14]LIUXW.AgeneralmodelofparameterizedOWAaggregationwithgivenornesslevel[J].InternationalJournalofApproximateReasoning,2008(48)：598-627.

Interval valued intuitionistic fuzzy number density weighted operator and its application in decision making

DU Yingxue, CHANG Juan, LIU Weifeng

(School of Science, Zhengzhou University of Aeronautics,Zhengzhou 450015, China)

In multiple attribute decision-making when the attribute value is interval valued intuitionistic fuzzy numbers, we consider the density degree of attribute information distribution, the interval valued intuitionistic fuzzy set data clustering problem. We propose new operator: linear interval valued intuitionistic fuzzy number density weighted averaging middle operator (IIFDWA) and the product of interval value intuitionistic fuzzy number density weighted averaging middle operator (IIFDWGA), which is referred to as the interval valued intuitionistic fuzzy density operator. Finally, the IIFDWA operator and the WAA are applied to the multiple attribute group decision making problems.

multi-attribute decision-making; interval valued intuitionistic fuzzy numbers; Interval valued intuitionistic fuzzy number density operator; clustering

2016-04-06

国家自然科学基金(11501525)；河南省基础前沿研究计划项目(152300410126)；河南省教育厅科学技术研究重点项目(14A630017)；郑州航空工业管理学院青年科研基金(2014113001)

杜迎雪(1979-)，女，河南许昌人，讲师，主要从事应用数学研究.

C934

A

1674-330X(2016)03-0075-05