混合策略下的理性交换协议模型

丁洪，彭长根，邝青青

（1. 贵州大学理学院，贵州 贵阳 550025；2. 贵州大学密码学与数据安全研究所，贵州 贵阳550025）

混合策略下的理性交换协议模型

丁洪1，2，彭长根1，2，邝青青1，2

（1. 贵州大学理学院，贵州 贵阳 550025；2. 贵州大学密码学与数据安全研究所，贵州 贵阳550025）

在小额支付的交换协议中，通过TTP保证协议公平性所需代价往往高于协议本身价值，在这种情况下，理性交换协议是一种合适的选择。应用扩展式博弈混合策略理论对交换协议进行了建模，引入熵函数对交换过程中的公平性进行了描述；在保证过程公平性原则的前提下，运用混合策略纳什均衡概念形式化定义了理性公平性，并在此模型基础上构造了一个新的理性交换协议；对协议的可追究性、理性公平性进行了证明，结果表明该协议能达到混合策略纳什均衡。该协议无须可信第三方，实现了理性公平性并对惩罚值进行了优化，具有更好的适应性。

理性交换协议；混合策略；过程公平；纳什均衡

中文分类号：TP309

1　引言

交换协议被广泛应用在电子合同签署、电子邮件认证和网络支付服务等领域，如何保证交换过程中各方参与者的公平性是交换协议的一个重要问题，目前，主要依赖于公平交换原则和理性交换原则来解决。传统的公平交换协议通常以可信第三方（TTP，trusted third party）或复杂的通信为代价来保证公平性的实现，可信第三方容易成为瓶颈。理性交换不需要可信第三方，在实现理性公平性的同时提高了效率，因此理性交换逐渐成为研究热点。在微支付协议中，保证强公平性的代价往往高于支付协议本身的价值，从而强公平性不再适用于这类协议，而理性交换能提供更合适的解决方法。

1998年，Asokan［1］首次将博弈论应用到公平交换协议的分析设计中，同年 Syverson［2］首次提出了理性交换的概念，即在交换过程中，参与者的不诚实行为可能会对其他参与者的利益造成损失，但是参与者不会因不诚实行为而获利。换言之，理性交换不能够完全保证公平性，但理性参与者没有理由偏离协议。2001年，Buttyan等［3］运用博弈论的方法给出了公平性的形式化定义，基于扩展式博弈对交换协议进行了建模并对Syverson协议进行了分析。针对Syverson协议中的不足，Alcaide等［4～6］应用不完全信息动态博弈理论，在交换协议中引入信念，建立了贝叶斯博弈下的理性交换协议模型，使理性交换更加符合现实应用环境。在文献［7］中，作者基于极大熵原理设计了一个新的理性交换协议，并对协议的安全性和公平性进行了证明。上述研究成果都只对交换协议的结果公平性进行了讨论，并未涉及过程公平性的分析。而本文考虑用信息论中的熵理论［8］对过程公平性进行描述，并探讨过程公平原则下的理性公平性。

本文应用扩展式博弈下的混合策略［9］对理性交换协议进行建模，给出此模型下的混合策略纳什均衡定义；通过引入熵理论对过程公平性进行描述，给出过程公平性的定义；在过程公平性原则下，利用博弈树对整个交换过程进行分析并给出协议的可追究性［10］、理性公平性的证明。结果表明该协议能达到混合策略纳什均衡。协议交换过程无须可信第三方，该协议实现了理性公平性并对惩罚值进行了优化，具有更好的适应性。

2　理性交换协议的混合策略模型

博弈论是研究决策问题的理论。在博弈过程中，参与者会极力猜测对方如何选择，同时又不想让对方猜到自己的选择，在这样的情况下，参与者往往会随机选择自己的策略。混合策略解释了一个参与者对其他参与者所采取行动的不确定性，它描述了参与者在给定信息下以某种概率分布随机地选择不同的行动或策略。可以通过引用熵对这样的不确定性进行描述。

在小额支付协议中，选择可信第三方来保证公平性所需的代价往往高于支付协议本身。在这种情况下，理性交换协议是一种合适的选择。而协议参与者进行信息交互的过程可以看作一个混合策略扩展式博弈过程，因此可以利用混合策略扩展式博弈理论对其进行建模。

2.1基础知识

1）混合策略

4）混合策略Nash均衡

2.2混合策略下的交换协议模型

下面将一个交换协议记为π，其执行的过程看作一个混合策略扩展式博弈进行的过程，则可以将交换协议描述为与扩展式博弈类似的七元组其中各元素的含义如下。

1）T：参与者集合。

4）P：参与者函数，用于计算非终点行动序列的下一个参与者。表示为对于任意非终点行动序列表示非终点行动序列q后的下一个参与者。

在对收益值进行计算的过程中，加入一个惩罚函数 F。在协议执行的每一轮中，只要参与者采取某种不诚实行为，就在他的收益值上减去相应的惩罚函数。在计算最终收益时将每一轮的惩罚值都算入收益结果中。

2.3混合策略下的理性公平性

定义3过程公平性原则。在协议执行过程中，若每个参与者在每个自己的可选行动集上的策略熵函数相等，即则该交换协议是过程公平的。

定义4混合策略Nash均衡。将有2个参与者的交换协议记为π′，将交换协议看为一个博弈，2个参与者分别为A和B，参与者的混合策略集分别记为若一个交换协议是混合策略Nash均衡公平的，则其存在一个混合策略组合满足

定义 5若一个交换协议在保证过程公平的前提下，能满足混合策略Nash均衡公平性，则称该协议为一个理性交换协议。

3　一种新的理性交换协议

3.1理性交换协议的构造

在以上的混合策略博弈模型的基础上，构建一个新的理性交换协议。假设进行通信的网络是可靠的，使用的加密方法是安全的，在保证过程公平的基础上，通过对收益函数进行调整，最终达到混合策略Nash均衡点，从而实现理性公平交换。

协议中有2个参与者A、B，A是商家，B是顾客。他们要交换的物品分别为假设他们用于交换的物品是等价的，即若协议正常执行，则参与者A、B的收益均为0。协议中用到弱秘密承诺函数（）w k，在一定的时间内，该函数无法破解。构造的协议如图1所示。

图1　理性交换协议交互过程

步骤2参与者B能观察到参与者A选择发送消息的概率分布，为了保证过程公平性，B采取与A相同的概率分布选择自己要发送的消息。假设参与者B是诚实且理性的，他可以选择发送的信息为

3.2理性交换协议的分析

下面从正确性、可追究性、公平性的角度对以上的理性交换协议进行分析。首先，分析了在混合策略下该理性交换协议的正确性；其次，用 Kailar逻辑对该协议进行了可追究性分析；最后，在过程公平性的原则下，基于博弈树对整个协议过程进行了描述，探寻了其混合策略Nsah均衡的存在性。

1）正确性

定理 1当交换协议正常执行完毕时，若协议主体A和B分别能够获得所交换的物品和，则上述基于混合策略下的理性交换协议是正确的。

证明通过协议的执行过程，可以看到，当协议完成后，参与者A能够获得消息并且 A可以利用自己的私钥通过解密算法获得经过一定的时间后，通过弱秘密承诺函数得到从而通过计算得到想要交换的商品

综上，当协议正常执行完毕时，各方参与者都能得到自己想要交换的商品itemA、itemB，即该混合策略下的理性交换协议是正确的。

2）可追究性

可追究性要求任何交易方必须为自己的行为负责，Kailar逻辑是专门针对电子商务可追究性进行分析的逻辑。其有如下基本原理。

用Kailar逻辑对上述协议进行形式化分析，若协议能满足一定的目标，则说明该协议在Kailar逻辑下满足可追究性。

定理 2在给定的初始状态假设下，该协议在Kailar逻辑下具有可追究性。

证明根据Kailar逻辑的定义，该协议保证可追究性必须满足的目标如下。

对于协议目标的推导有关的部分语句解释如下。

引入如下初始状态假设。

根据上述假设，利用Kailar逻辑进行如下推理。

当B收到消息①时，可得

由假设A3和签名原理得

再由假设A5和推断原理得

即满足G2。

当A收到消息②时，可得

由假设A1和签名原理得

在由假设A4和连结原理得

最后，由假设A6和推断原理得

即满足G1。

同理可证目标G3、G4能被满足。

因此，该协议在Kailar逻辑下具有可追究性。

3）公平性

根据上述建立的模型，利用博弈树对整个协议过程进行描述，如图2所示。

第二轮由参与者B开始选择行动。参与者B不能够区分A发送的消息是还是但是，B能够观察到A在可选行动集上的概率分布。此时参与者B的信息集为了达到过程公平，即参与者B不想让参与者A通过自己的行动推测到更多的信息，B选择以和A相同的概率分布选择自己的行动。此时在上的混合策略为，混合策略熵函数若参与者B选择行动，则博弈终止；若B选择第二轮结束进入第三轮，双方受益待定。

下面分析此交换协议的公平性。在博弈过程中，每个参与者会极力猜测对方如何选择，同时又不能让对方猜到自己的选择，为了使对方猜不透自己的选择，会随机选择自己的策略，即以一定的概率分布去选择自己的策略。通过分析，可以知道如下信息。

参与者A的纯策略集为

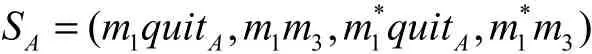
相应的混合策略为

参与者B的纯策略集为

相应的混合策略为

则可以得到如图3所示的收益矩阵。

图2　交换协议的博弈树描述

图3　收益矩阵

下面讨论在什么条件下混合策略组合

为混合策略Nash均衡。

在过程公平的原则下，为了保证每一轮中的混合策略熵函数不变，假设θ=α=β。所以，参与者 A在混合策略组合下的期望收益为

当参与者B选择混合策略σB时，A选择各个纯策略的期望收益为

同理，可以对参与者B在混合策略

下的期望收益进行讨论。

当参与者 A选择混合策略σA时，参与者 B选择纯策略m2、quitB的期望收益为

通过以上分析可以看到，在所构造的新的理性交换协议中，惩罚值并非越大越好。参与者遵守协议的概率与惩罚值和交换物品本身的价值之比有关。在这样的情况下，可以通过对惩罚值的设定控制参与者遵守协议的概率分布，从而更好地促使参与者遵守协议。

3.3实例分析

表1　成本与选择概率之间的关系

可以看到，随着商家给出折扣的升高，顾客B在得到实惠的同时，所面临风险的不确定度也在增大。此时商家的报价越接近商品的实际价值，则协议正常执行的概率就越大。而这时若随意改动惩罚值，则有可能找不到满足条件的θ。那么，原有的协议博弈在没有均衡解的情况下，很难保证协议的正常进行。而对于惩罚值的设定，并非越高越好。在所提出的模型中，过高的惩罚值反而会降低θ最大值的取值，让商家望而却步，从而降低了商家诚信参与协议的概率。

4　结束语

本文在假设加密方法安全、网络通道可靠的前提下，引入熵理论对协议交换过程中的不确定性进行描述，进而给出过程公平的定义，并在保证过程公平的原则下，应用扩展式博弈下的混合策略理论对理性交换协议进行建模。结合所建模型和博弈论中混合策略Nash均衡的定义，本文对理性交换协议做了形式化的定义，并构造了一个新的理性交换协议。而当网络不一定可靠以及过程不一定严格公平时，如何建立一个基于扩展博弈的协议博弈模型，在这样的模型中交换协议是否依然满足理性公平将是进一步研究的方向。

［1］ASOKAN N. Fairness in electronic commerce［D］. Waterloo：University of Waterloo，1998.

［2］SYVERSON P. Weakly secret bit commitment：applications to lotteries and fair exchange［C］//The 11th IEEE Computer Security Foundations Workshop. c1998：2-13.

［3］BUTTYAN L. Building blocks for secure services：authenticated key transport and rational exchange protocols［D］. Lausanne：Ecole Polytechnique Federale de Lausanne，2001.

［4］ALCAIDE A，ESTEVEZ-TAPIADOR J M，HERNANDEECASTRO J C，et al. An extended model of rational exchange based on dynamic games of imperfect information［C］//International Conference on Emerging Trends in Information and Communication Security. c2006：396-408.

［5］ALCAIDE A. Rational exchange protocols［D］. Leganés：Universidad Carlos III de Madrid，2008.

［6］ESTEVEZ-JAPIADOR J M，ALCAIDE A，HERMANDEZCASTRO J C，et al. Bayesian rational exchange［J］. International Journal of Network Security，2008，7（1）：85-100.

［7］吕桢，彭长根，刘海. 基于极大熵原理的理性公平交换协议［J］.计算机应用研究，2014，31（2）：563-567. LV Z，PENG C G，LIU H. Rational fairness exchange protocols based on maximum entropy principle［J］. Application Research of Computers，2014，31（2）：563-567.

［8］陈运. 信息论与编码［M］. 北京：电子工业出版社，2007. CHEN Y.Information theory and coding［M］. Beijing：Publishing House of Electronics Industry，2007.

［9］朱·弗登博格，让·梯若儿. 博弈论［M］. 黄涛，译. 北京：中国人民大学出版社，2010. FUDENBERG D，TIROLE J. Game theory［M］. Translated by HUANG T. Beijing：China Renmin University Press，2010.

［10］王可心，韩芳溪. Kailar逻辑推理中初始状态假设［J］. 大连理工大学学报，2003，43（1）：193-196. WANG K X，HAN F X. Initial state assumptions in Kailar logic reasoning［J］. Journal of Dalian University of Technology，2003，43（1）：193-196.

Rational exchange protocol model based on mixed strategy

DING Hong1，2，PENG Chang-gen1，2，KUANG Qing-qing1，2

（1. College of Science，Guizhou University，Guiyang 550025，China；2. Institute of Cryptography & Data Security，Guizhou University，Guiyang 550025，China）

In the exchange of micropayment protocol，the cost of ensuring fairness by TTP is higher than the value of protocol，in this case the rational exchange protocol is a appropriate choice. Exchange protocol was modeled by extensive mixed strategy game and the entropy function was introduced to discuss the fairness in the process of exchange. In addition，the rational fairness was formally defined by using the concept of mixed strategy Nash equilibrium under the principle of the fairness in the process，and on the basis of this model to construct a new rational exchange protolcol. The protocol's accountability and rational fairness were proved，the results show that the proposed protocol can achieve mixed stratrgy Nash equilibrium. Without the participation of the trusted third party，the protocol can achieve rational fairness and optimize the penalty values，it is beautifully adapted to the real environment.

rational exchange protocol，mixed strategy，process fairness，Nash equilibrium

A

10.11959/j.issn.2096-109x.2016.00016

2015-11-11；

2016-01-09。通信作者：彭长根，peng_stud@163.com

国家自然科学基金资助项目（No.61262073）；全国统计科学研究计划基金资助项目（No.2013LZ46）；贵州省统计科学研究课题基金资助项目（No.201511）

Foundation Items：The National Natural Science Foundation of China（No.61262073），The National Statistical Scientific Research Project（No.2013LZ46），The Guizhou Provincial Statistical Science Research Project（No.201511）

丁洪（1991-），女，贵州安顺人，贵州大学硕士生，主要研究方向为密码学理论与工程。

彭长根（1963-），男，侗族，贵州锦屏人，博士，贵州大学教授、博士生导师，主要研究方向为密码学、信息安全。

邝青青（1988-），男，贵州安顺人，贵州大学硕士生，主要研究方向为密码学理论与工程。