冲击响应谱与经典冲击试验等效计算方法
杨 博,陈立伟,冯 伟,张 冰(1. 北京强度环境研究所,北京 100076;2. 天津航天瑞莱科技有限公司,天津 300462)
冲击响应谱与经典冲击试验等效计算方法
杨 博1,2,陈立伟1,2,冯 伟1,2,张 冰1,2
(1. 北京强度环境研究所,北京 100076;2. 天津航天瑞莱科技有限公司,天津 300462)
产品即使在试验室里通过了经典冲击试验环境,在实际使用环境中还有损坏。因此简单采用经典冲击作为检测条件的试验规范已经不能满足使用需求。另外,试验中,给定的波形量级与脉宽往往超出电动振动台或冲击台的性能范围,阻碍了试验的顺利进行。基于等效冲击试验原理,采用冲击响应谱(SRS)代替经典冲击。运用改进的递归数字滤波法编制经典脉冲的冲击响应谱计算程序,实现了经典冲击与冲击响应谱的等效计算。算例和试验表明,方法合理可行。
经典冲击;冲击响应谱;等效冲击
引言
产品在使用过程中会受到冲击载荷的作用。为了考核、评定产品在冲击作用下的电性能、机械性能及结构强度,进一步提高可靠性,须对产品进行冲击试验。冲击试验一般分为经典冲击和冲击响应谱两种。经典冲击一般有半正弦波、梯形波和锯齿波三种,实践证明,部分产品试件即使在试验室里通过了用经典冲击即半正弦、梯形波和锯齿波做的冲击试验,在野外和实际环境中还有损坏;或者在试验室里没有通过经典冲击试验环境,但在实际使用环境中却未见异常。因此简单采用经典冲击作为检测条件的试验规范已经不能满足使用需求。随着试验技术的发展,冲击响应谱试验规范在越来越多的被提及和使用。目前在动力学环境试验中,用冲击响应谱试验代替经典冲击试验来模拟试验件遭受的各种冲击环境也是冲击试验技术的发展趋势,GJB 150A中明确规定只有证明测量数据在经典脉冲的容差内,才允许采用后峰锯齿脉冲与梯形脉冲,其他均以冲击响应谱作为瞬态冲击的试验标准。和经典波形的冲击相比,冲击响应谱试验研究冲击的目的不仅研究冲击波本身,而且重点关注冲击作用与系统的效果,研究冲击对系统的损伤,并且冲击响应谱试验可以更真实的模拟冲击环境,很好的解决了传统经典冲击对产品施加的过冲击,对系统的预检作用也更准确更安全;而且冲击响应谱试验对冲击脉冲的类型和产生冲击的方法不做严格的要求,试验的灵活性较大。
另外,对于部分产品,需要依照之前标准对产品施加的脉冲持续时间长或冲击峰值加速度幅值大的经典冲击试验条件,而电动振动台系统或冲击台系统受设备性能参数的限制,不能实现此类检测试验环境。通过将经典冲击转化为冲击响应谱,很好的解决此类问题,并且冲击响应谱曲线将更能再现其真实的工作环境。目前国内对等效冲击条件的转换研究较少。
1 等效试验原则
1.1冲击响应谱的定义
冲击响应谱(SRS)描述了在冲击载荷作用下一系列有阻尼单自由度系统(SDOF)最大响应绝对值同该系统固有频率之间的关系,为频域内提供了基于冲击载荷下的响应估计值[1]。冲击响应谱与冲击载荷的傅里叶频谱不同,傅里叶频谱研究冲击载荷本身在频域的能量分布属性,它只是冲击载荷频域中通过傅里叶变换的展开,不涉及任何机械系统的响应。即使冲击响应谱与傅里叶频谱两者都是频率的函数,但两者所表达的内容有本质的不同。
1.2等效基本原理
冲击试验是为了考核试验件在冲击载荷作用下环境适应性和结构完好性,从损伤原理上讲,冲击试验可以简单定义为一种强度试验,不考核产品的疲劳强度,没有传统意义的应力循环次数的定义,因此Miner疲劳损伤理论[2] [3]在冲击试验中并不适用。
在试验件进行冲击试验时,应使试验室冲击环境作用下试件的损伤及故障模式与实际使用过程中冲击环境所产生的影响相当。这里提到的损伤及故障模式包含试验件的结构强度、结构完整性,试验件的功能等方面。冲击试验的等效关系基于冲击响应,冲击响应可用最大位移响应、最大速度响应、最大加速度响应相等来实现。在试验室实际应用中,用最大加速度响应来实现等效环境便于应用,因此可以说:如果试验件在冲击作用下的最大加速度响应相等,则可认为冲击脉冲对试验件的损伤也相当[4]。
2 计算方法
2.1冲击响应谱的数值计算方法—改进的递归数字滤波法
冲击响应谱的数值计算方法可以分为早期和目前使用两大类。早期的数值解法有直接积分法,FFT变化法,递推法和递归数字滤波法,目前比较成熟的冲击响应谱的数值解法是由Smallwood提出的改进的递归数字滤波法。该方法舍弃了常用的激冲不变的滤波器模型,设计了一种新颖的斜坡不变模型。其计算方法如下[5][6]:
设单自由度系统基础加速度输入U(t)的采样值为Uk,k=0,1,…,N。
单自由度系统的绝对加速度响应为Xk,k=0,1,…,N。则有:
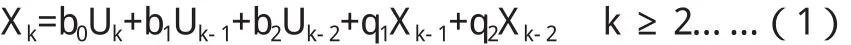
式中:
b0=1-exp(-D)sin(E)/E
b1=2exp(-D)[sin(E)/E-cos(E)]
b2=exp(-D)[exp(-D)-sin(E)/E]
q1=2exp(-D)cos(E)
q2=-exp(-2D)
D=ζ ω△t
E=ωd△t

△t─采样间隔
ζ─ 系统阻尼系数
2.2算例
GJB 150与GJB 150A均对没有测量数据时飞行器设备的功能性冲击与坠撞安全冲击的试验条件进行定义,如表1和表2所列,该条件在MIL-STD-810F中也有体现。
采用改进递归数字滤波法计算两半正弦冲击环境的冲击响应谱,Q因子取10,图1(a)、(b)为计算冲击响应谱和与之对应的目标谱曲线。
一个完整的冲击响应谱试验条件一般包括频率范围、斜率、拐点频率、冲击量级。
1)频率范围的选取
试验条件的频率范围一般根据试验件的结构决定,综合考虑试验件的工作频率范围。但是频率范围需要包含冲击响应谱曲线中缓冲区,放大区与等冲区,由试验件的固有频率与冲击脉冲的持续时间决定。
2)斜率的选取
冲击响应谱试验条件斜率k为冲击响应谱试验曲线中上升段斜率,单位取dB/oct,计算方法如公式(2):
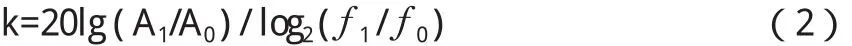
f0,f1─ 冲击响应谱起始频率,拐点频率;
A0,A1─ 起始频率、拐点频率处的加速度量值
在由经典冲击计算出的冲击响应谱中任一频率点处的斜率计算方法见公式(3):
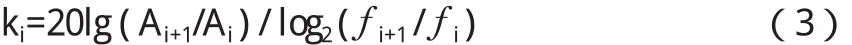
fi,fi+1─ 起始频率,与之相邻点频率;
Ai, Ai+1─ 起始频率、与之相邻频率处的加速度量值
起始段一般包含经典冲击计算冲击响应谱的缓冲区与放大区,图2给出了计算冲击响应谱起始段斜率曲线。从该图可以看出,在初始段区域任一点的斜率随着频率的增加而减小,起始段频率处斜率变化不大,越靠近放大区衰减的越快,因此等效目标谱斜率的选取应根据试验条件频率范围初始频率附近的斜率,能更好的包络冲击试验的最大响应。GJB 150A中斜率的选取与此原则一致,表3、4的两个试验条件k=6 dB/oct,计算冲击响应谱的起始频率为k=5.86 dB/oct。
3)拐点的选取
对于经典脉冲冲击等效的冲击响应谱目标谱,拐点的选取要避开放大区对试验件在低频段的过试验,使试验冲击环境更合理有效的模拟真实冲击环境。
图3为计算冲击响应谱不同频率处的斜率变化量,即△ ki=ki+1-ki,通过分析发现拐点的取值为斜率变化量最大的频率处。

表1 飞行器设备功能性冲击与追撞安全冲击试验条件(GJB 150)

表2 飞行器设备功能性冲击试验条件(GJB 150A)
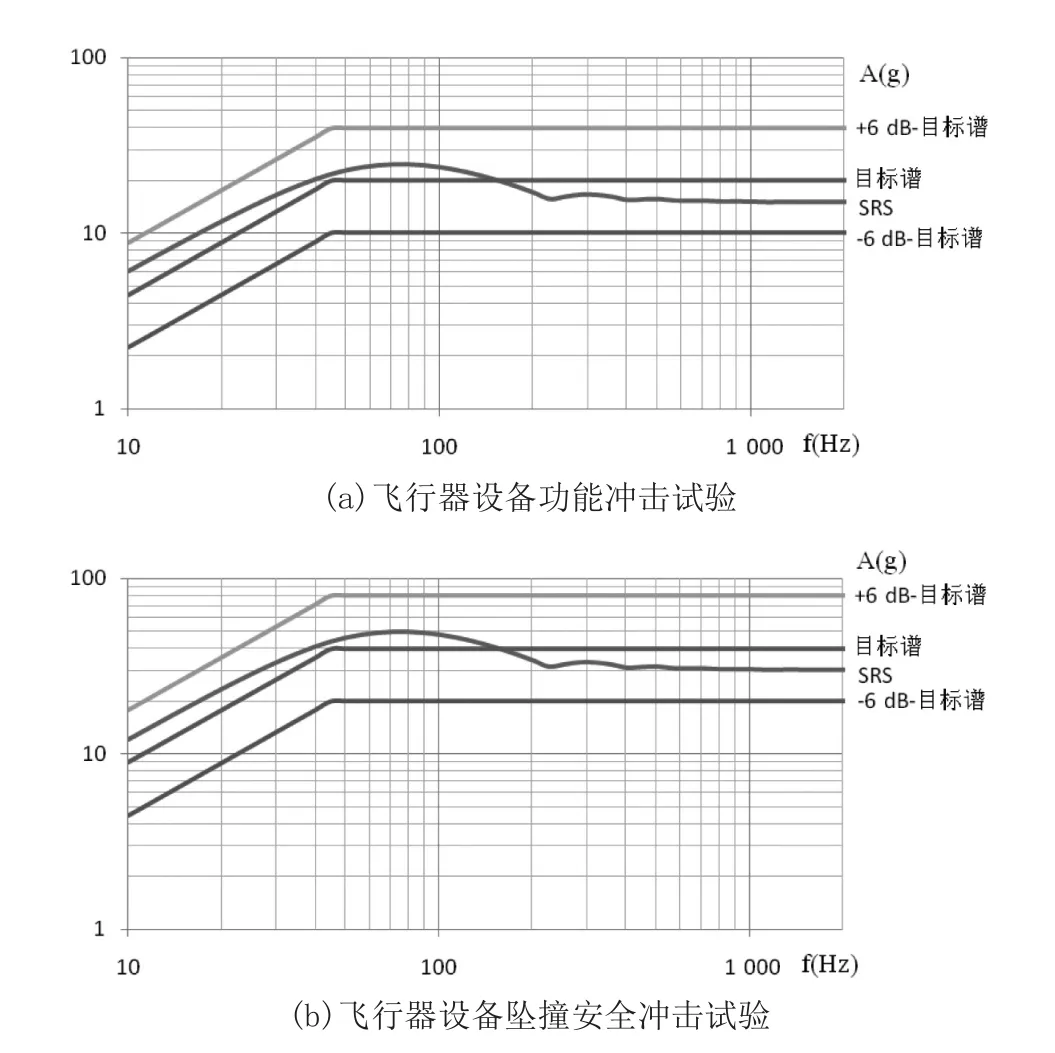
图1 GJB 150半正弦脉冲计算冲击响应谱与GJB 150A冲击响应谱目标谱
4)冲击量级
冲击量级为冲击响应谱中平直段加速度,平直段的加速度量值的选取决定对试验件力学环境考核的严酷程度。若其量值选取放大区的峰值响应加速度,则会造成在高频段对试验件的严重过实验;若其量值选取等冲区的峰值响应加速度,则会造成在低频段对试验件的考核出现欠试验。综上考虑,半正弦脉冲的冲击响应谱对应的等效冲击响应谱目标谱的冲击量级取半正弦冲击的放大区峰值响应加速度与等冲段的峰值响应加速度的平均值较为合适,如表3所示。
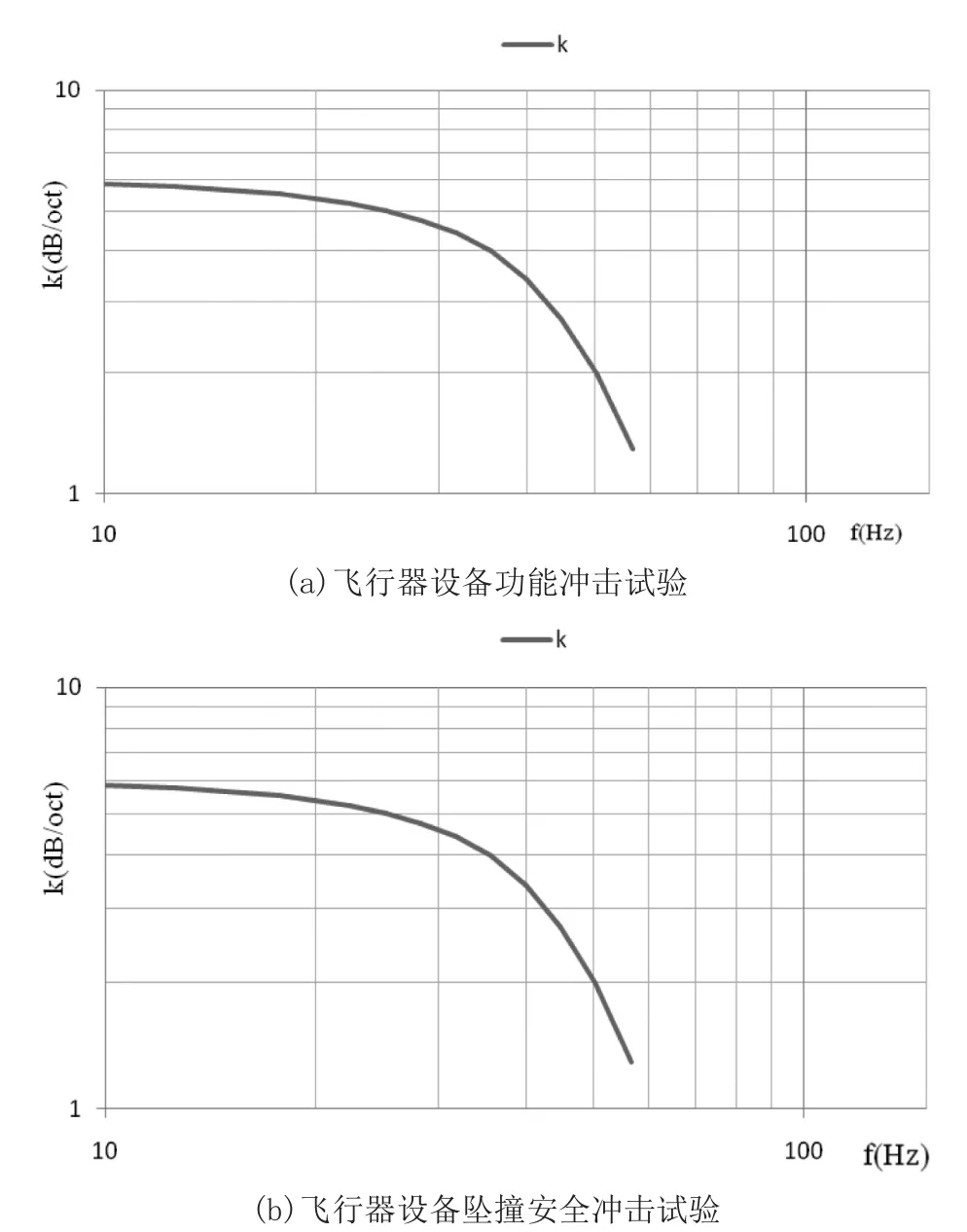
图2 半正弦脉冲计算冲击响应谱起始段斜率
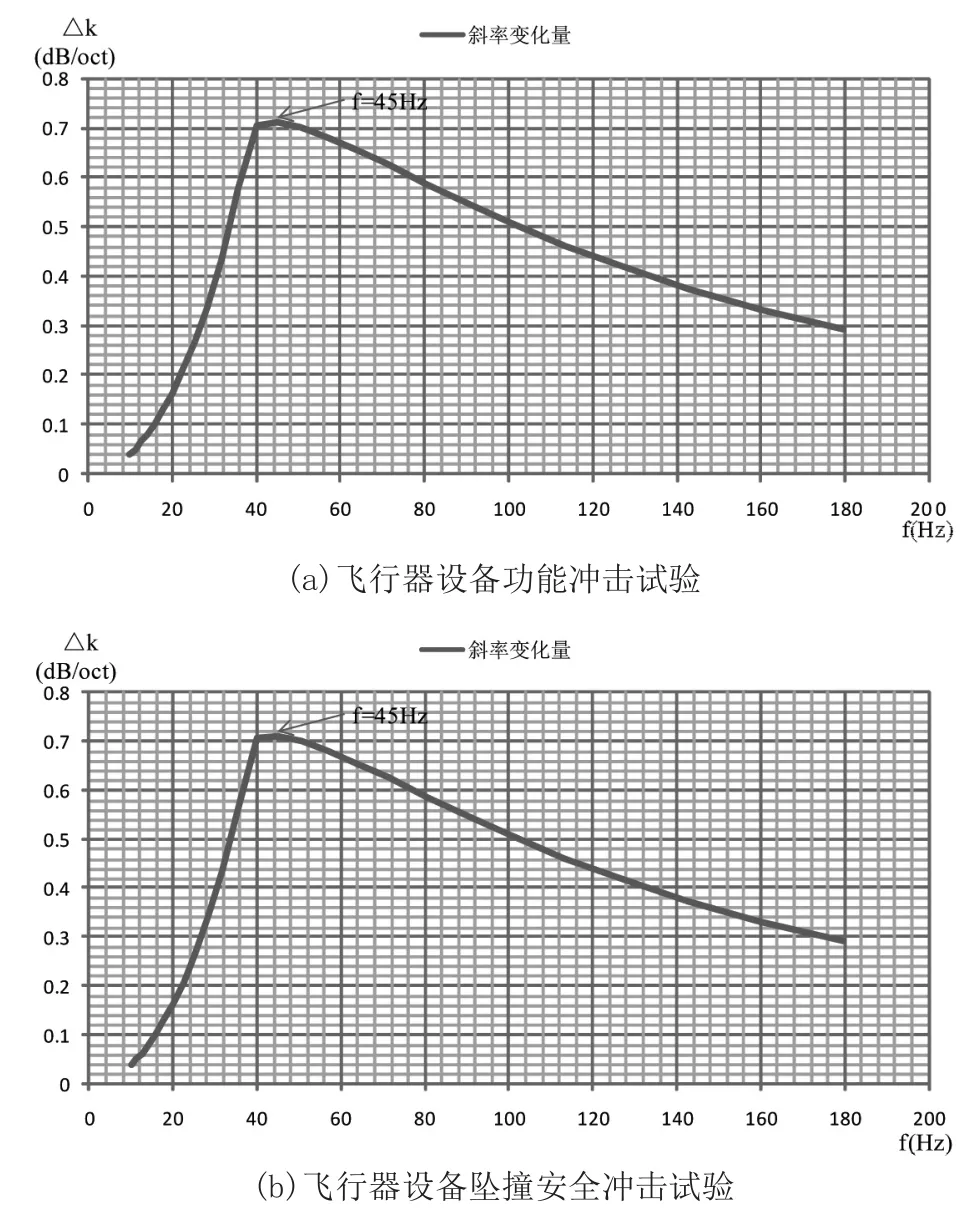
图3 半正弦脉冲计算冲击响应谱起始段斜率变化量
3 试验验证
某冲击试验条件为半正弦脉冲,A=1 260 g,D=0.4 ms,为某试验标准中经典冲击试验条件。目前的电动振动台或冲击台均不能模拟此冲击条件。为了实现对产品进行此类冲击环境的考核,应用本文提出的计算方法计算其等效的冲击响应谱,并在摆锤式冲击台上实现此冲击环境。
步骤1:改进递归数字滤波方法计算该经典脉冲的冲击响应谱,见图4。
步骤2:拐点
步骤3:斜率
冲击响应谱初始频率段斜率见图6,计算冲击响应谱的起始频率为k=6 dB/oct。
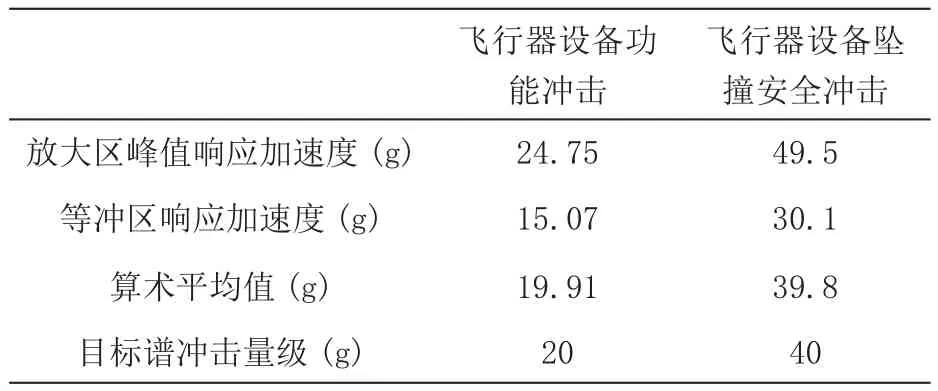
表3 冲击响应谱试验冲击量级
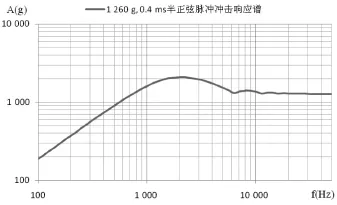
图4 半正弦脉冲冲击响应谱
步骤4:冲击量级
冲击量级的选取为放大区峰值响应加速度与等冲区响应加速度的算术平均值。
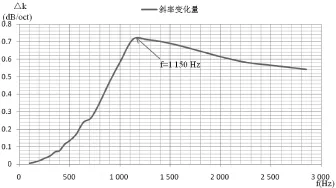
图5 半正弦脉冲冲击响应谱起始段斜率变化量
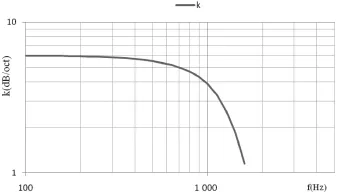
图6 半正弦脉冲冲击响应谱起始段斜率

表4 冲击响应谱试验冲击量级
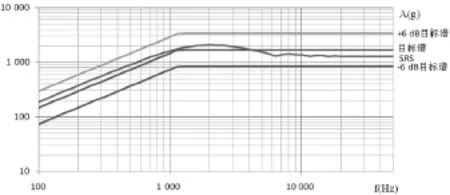
图7 计算冲击响应谱与目标谱
计算冲击响应谱与经过等效转化后的冲击响应谱目标谱如图7所示,由该图可以看出,半正弦脉冲冲击响应谱能很好的包络在得出的目标谱的±6dB容差限范围内。
4 结束语
冲击响应谱试验技术是冲击试验的发展方向。目前,美国等发达国家的冲击响应谱技术比较成熟,以美军标MIL-STD-810F为代表的冲击试验规范要求只有证明测量数据在经典脉冲的容差内,才允许采用后峰锯齿脉冲与梯形脉冲,其他均以冲击响应谱作为瞬态冲击的试验标准。而我国冲击响应谱技起步较晚,目前仅在GJB 150A中规定了某些特定的试验采用冲击响应谱技术,大部分冲击试验还沿用GJB 150中的半正弦脉冲、后峰锯齿脉冲。对于没有实测数据而采用冲击试验标准的大量级经典冲击试验条件,可以考虑采用此方法进行等效转化。而对于已经证明的测量数据为经典脉冲的试验条件,采用此冲击等效计算方法的合理性还需要进一步验证。
随着冲击响应谱试验技术与试验装置和软件在国内的普及和推广,用冲击响应谱试验代替经典冲击将成为一种趋势,将会有很大的发展空间。
[1]胡志强等. 随机振动试验应用技术[M]. 北京:中国计量出版社,1996.12.
[2]力学环境实验技术编著委员会.力学环境实验技术[M] .西安:西北工业大学出版社, 2003.
[3]冯睿,王宗峰. 冲击试验的等效试验[J].试验技术与试验机, 2007 (01): 41-43+57.
[4]李蓓蓓.冲击响应谱的规律[J].包装工程, 2004(01): 12-13+29.
[5]骞永博.冲击响应谱试验技术研究[D] .西安:西北工业大学, 2007.
[6]David O. Smallwood, An Improved Recursive formula for Calculating Shock Response Spectra, Shock and Vibration Bulletin No. 44, Part 3, pp 43-56,Aug. 1974.
Research on Equivalence Experimentation of SRS Test and Classical Shock Test
YANG Bo1,2, CHEN Li-wei1,2, FENG Wei1,2, ZHANG Bing1,2
(1. Beijing Institute of Structure and Environment Engineering, Beijing 100076;2. Tianjin Aero-space Relia Technology Co., Ltd., Tianjin 300462)
Although most specimens pass the classical shock test, it also will make mistake in actual situation. Therefore, if simply adopting classical shock test as the test conditions, this test specification can't meet the use requirements any more. In some classical shock tests, the experimental conditions always exceed the test range of electro-dynamic shakers, which bring many difficulties to our work. Based on the equivalence experimentation on shock test, this paper puts forward using SRS test instead of classical shock test. A computation program about SRS is written based on improved recursive formula. Finally, the paper summarizes the approach to fix SRS test conditions equivalence to classical shock test.
classical shock; SRS; shock equivalence
V216.5
A
1004-7204(2016)04-0011-05
杨博(1986-),男,山东菏泽人,硕士,工程师,研究方向:结构强度、振动与可靠性。

