星形映照的新子族与Roper-Suffridge延拓算子
王朝君,崔艳艳,朱思峰
(周口师范学院数学与统计学院,河南 周口 466001)
星形映照的新子族与Roper-Suffridge延拓算子
王朝君,崔艳艳,朱思峰
(周口师范学院数学与统计学院,河南 周口 466001)
在Reinhardt域上及复Banach空间单位球上讨论了星形映照的一类新子族,即复数λ阶殆星映照.证明了几类推广的Roper-Suffridge延拓算子保持复数λ阶殆星映照的不变性,从而能够在多复变数空间的不同区域中构造复数λ阶殆星映照,所得结果推广了已有的结论.
星形映照;殆星映照;Roper-Suffridge算子
1 预备知识
单复变几何函数论中有许多优美的结论,例如单叶全纯函数的增长、掩盖定理等.然而在将这些结论推广到多复变数空间的过程中,人们发现即便是“在单位圆盘上全纯单叶函数展开式的系数的模是有界的”这样的基本结果,在多复变数中也不成立.后来人们考虑对映照加以几何上的限制,从而讨论具有特殊几何形状的双全纯映照,例如星形映照、凸映照、螺形映照等. 目前对于星形映照和凸映照已经有了许多很好的结论,近年来许多学者开始讨论他们的子族.[1-7]
2010年,Bălăeti和Nechita[8]引入了Cn中单位球上星形映照的新子族:复数λ阶殆星映照的定义.2013年,赵燕红[9]将复数λ阶殆星映照的定义推广到Reinhardt域及复Banach空间单位球上,研究了复数λ阶殆星映照与Loewner链的关系,得到了复Banach空间单位球上复数λ阶殆星映照的解析特征.然而在多复变数空间中很难找到具体的复数λ阶殆星映照的例子,但是若借助Roper-Suffridge算子[10],则可以由单复变中的复数λ阶殆星函数构造出许多多复变数空间中的复数λ阶殆星映照.
本文主要讨论Reinhardt域上及复Banach空间单位球上复数λ阶殆星映照在一些推广的Roper-Suffridge算子下的不变性.文中用D表示单位圆盘,B表示复Banach空间X中的单位球.
定义1[9]设Ω⊂Cn是有界星形圆形域,其Minkowski泛函ρ(z)除去一个低维流形域外一阶可导.令λ∈C,Reλ≤0,f是Ω上的正规化局部双全纯映照,若
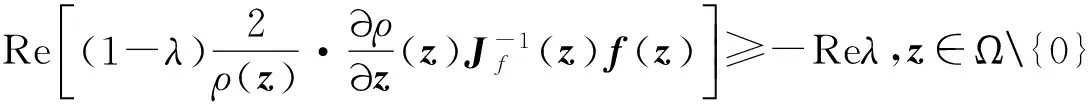

定义2[9-10]设f:B→X是一个正规化局部双全纯映照.若λ∈C,Reλ≤0且Re{(1-λ)Tx[(Df(x))-1f(x)]}≥-Reλ‖x‖,x∈B{0},则称f是B上的复数λ阶殆星映照.
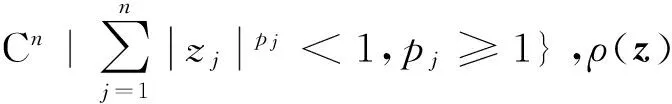
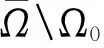
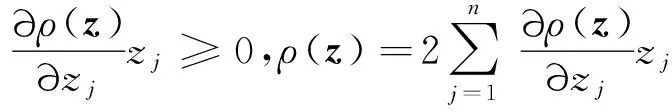
2 主要结论及其证明.

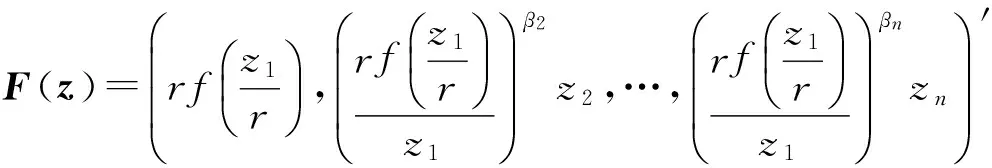
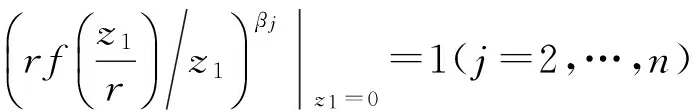

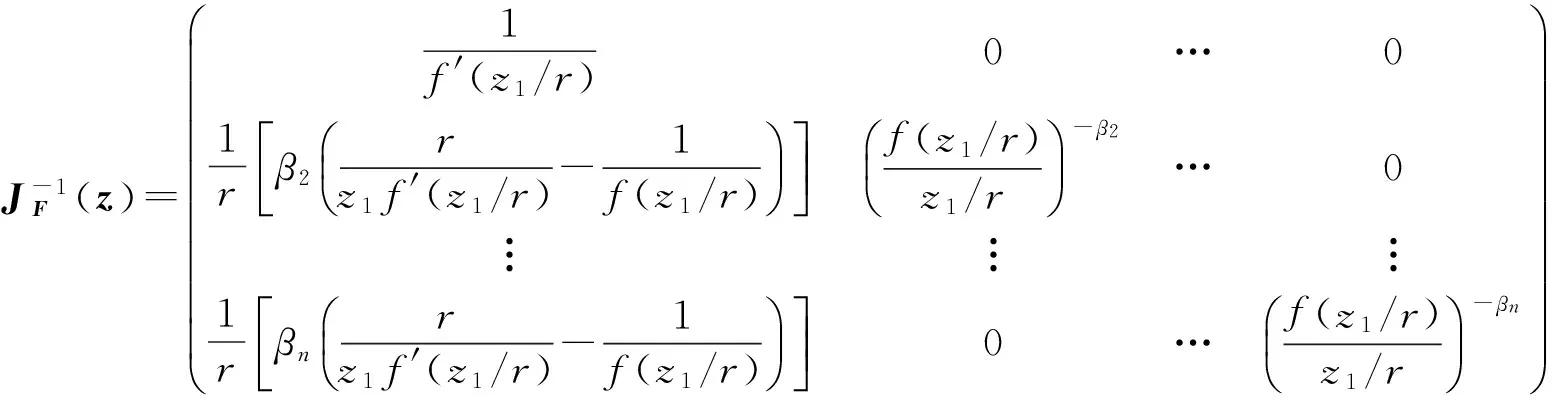
则
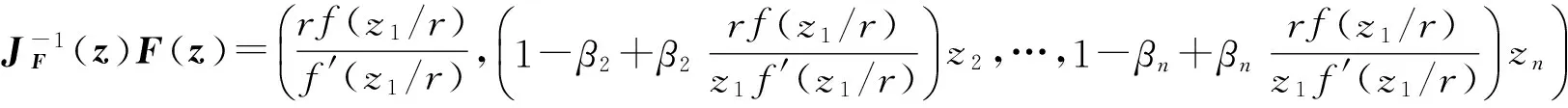
由引理1知
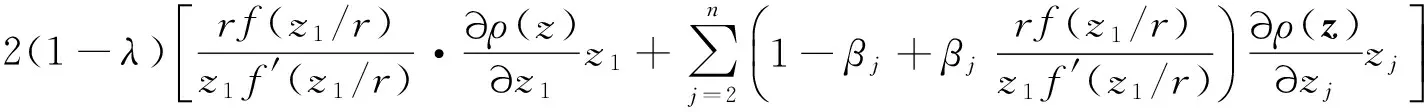
由于f是D上的复数λ阶殆星函数,则
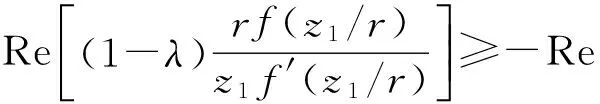
(1)
由(1)式及引理2知
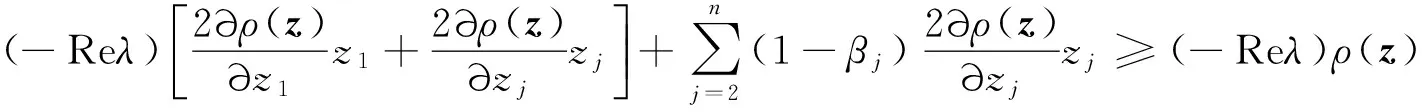
定理得证.

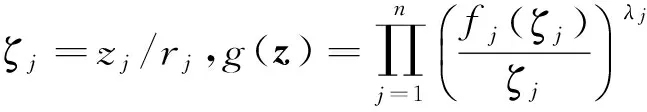

由于fj是D上的复数λ阶殆星函数,


从而 Jg(z)z+g(z)≠0.又显然F(0)=0,JF(0)=I,故F(z)是Ω上的正规化局部双全纯映照,且
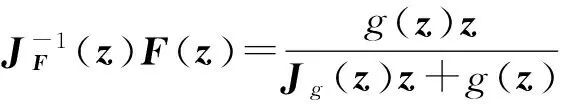
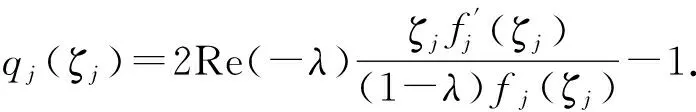

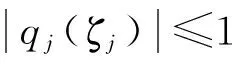

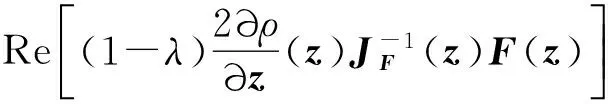

证明与定理2同理可得,这里不再赘述.
定理4设f是D上的复数λ阶殆星函数,β1=1,βj∈[0,1](j=2,…,n-1).则
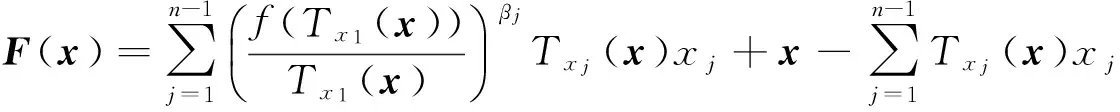
证明由文献[14]可知F(x)是复Banach空间单位球B上的正规化双全纯映照,且

由于f是D上的复数λ阶殆星函数,则
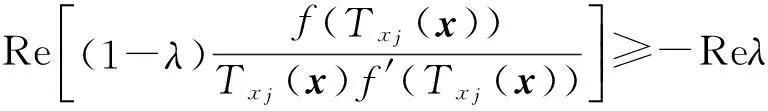
从而
Re{(1-λ)Tx[(DF(x))-1F(x)]}=
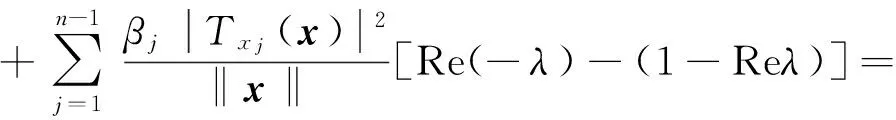
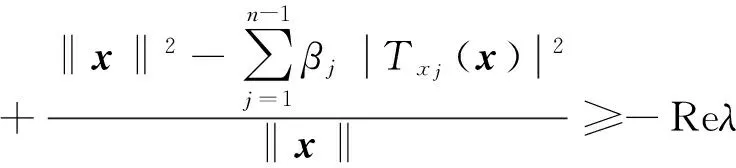
由定义2知定理得证.
[1]FITZGERALD C H,THOMAS C R. Some bounds on convex mappings in several complex variables[J]. Pacific J of Math,1994,165:295-320.
[2]BARNARD R W,FITZGERALD C H,GONG S. The growth and 1/4-theorem for starlike mappings inCn[J].Pacific J of Math,1991,150:13-22.
[3]龚升.多复变数的凸映照和星形映照[M].2版.北京:科学出版社,2003:182-227.
[4]崔艳艳,刘爱超. 一类强α次殆星形映照的增长和掩盖定理[J]. 东北师大学报(自然科学版),2014,46(1):17-21.
[5]冯淑霞,刘太顺,任广斌.复Banach空间单位球上几类映射的增长掩盖定理[J].数学年刊,2007,28A(2):215-230.
[6]徐庆华,刘太顺.正规化双全纯映照的增长和掩盖定理[J].数学年刊,2009,30A(2):213-220.
[7]王建飞.Cn中一类星形映射子族的增长定理及推广的Roper-Suffridge算子[J].数学年刊,2013,34A(2):223-234.
[8]BAlAETI C M,NECHITA V O. Loewner chains and almost starlike mappings of complex orderλ[J].Carpathian J Math,2010,26(2):146-157.
[9]赵燕红.复Banach空间单位球上的复数λ阶殆星映射[D].金华:浙江师范大学,2013.
[10]ROPER K A,SUFFRIDGE T J. Convex mappings on the unit ball of Cn[J]. J Anal Math,1995,65:333-347.
[11]刘名生,朱玉灿.有界完全Reinhardt域上推广的Roper-Suffridge算子[J].中国科学A辑,2007,37(10):1193-1206.
[12 ]闫春燕.Roper-Suffridge 算子与Loewner链[D].开封:河南大学,2008.
[13]刘小松.多复变数几何函数论中某些双全纯映照子族的性质[D].合肥:中国科学技术大学,2004.
[14]崔艳艳,王朝君.复Banach空间上推广的Roper-Suffridge延拓算子[J].数学杂志,2014,34(3):515-520.
(责任编辑:李亚军)
New subclass of starlike mappings and Roper-Suffridge extension operators
WANG Chao-jun,CUI Yan-yan,ZHU Si-feng
(Mathematics Department,Zhoukou Normal University,Zhoukou 466001,China)
A kind of new subclass of starlike mappings,namely almost starlike mappings of complex orderλ,on Reinhardt domains and on the unit ball in complex Banach spaces is studied. From the definitions,it is proved that some generalized Roper-Suffridge operators preserve the invariance of almost starlike mappings of complex orderλ,thus it can construct almost starlike mappings of complex orderλon different domains in several complex variables. The results extend the existing conclusion.
starlike mappings;almost starlike mappings;Roper-Suffridge operator
1000-1832(2016)03-0021-04
2015-03-30
国家自然科学基金资助项目(11271359,U1204618);河南省科技厅科技发展计划项目(102400450003);周口师范学院青年基金资助项目(zknub3201608);河南省高等学校重点科研项目(17A110041).
王朝君(1981—),男,硕士,讲师,主要从事多复变函数论及微分方程研究;通信作者:朱思峰(1977—),男,博士,副教授,主要从事复分析研究.
O 174.56[学科代码]110·41
A
[DOI]10.16163/j.cnki.22-1123/n.2016.03.005

