火灾工况下隧道衬砌结构内部温度场分析
于 涛 李雪进 徐晨亮 李炎锋 杨 超
火灾工况下隧道衬砌结构内部温度场分析
于 涛 李雪进 徐晨亮 李炎锋 杨 超
本文运用解析的方法研究了在火灾高温的条件下,城市地下公路隧道的衬砌结构的温度场分布及其发展情况。通过对比已有实验结果、运用数值模拟等方法验证了所建立衬砌内部温度计算公式的准确性。研究结果表明火灾情况下,城市地下公路隧道的衬砌结构表面具有很大的温度恒速率,明确了城市地下公路隧道施加防火保护的必要性。
随着地下交通隧道的迅速发展,人们的生活也变得更加便捷,然而,由于隧道内相对来说比较封闭,所以隧道火灾给人们带来的损失是巨大的。通过对大量的火灾案例进行调查分析得出,隧道内一旦发生火灾,一方面,隧道内人员的安全就会受到严重威胁,另一方面,隧道的衬砌结构的稳定性也会受到火灾高温的影响。衬砌结构内部的温度变化对于结构本身的承载力等性能有着很大的影响,而反过来,结构的承载力对于结构内部温度场的变化的影响很小,所以说,在进行隧道结构防火设计时的首要任务就是结构内部的温度场分析 。
就目前对于隧道衬砌结构的研究而言,主要有三种方法来确定隧道内衬砌结构的内部温度场分布:解析计算,数值模拟和实验研究。但不同方法的计算结果往往产生较大差别,所以有必要对各种计算方法进行总结,并对计算结果进行对比分析。
隧道的火灾场景
对于隧道内的衬砌结构的内部温度场计算的前提条件是隧道内火灾场景的确定。通过进行大量的理论分析以及试验,最后结果表明,升温速率、最高温度以及火灾的持续时间是影响隧道内衬砌结构在火灾中的行为因素。
(1)升温速率
由于隧道内部空间与外界是封闭的,所以说,相比于开放式空间来说,隧道火灾的最为显著的特点就是具有极快的升温速率,一般来说,在短短几分钟内就可达到1000℃甚至更高。隧道内的火灾温升速率的大小与燃烧车辆的类型有关。欧洲的尤里卡系列火灾实验研究了不同类型车辆燃烧时的温升速率,并得出结论:对于初期火灾来说,重型货车的温升速率要比小汽车的温升速率快。在本研究中,考虑到研究对象为城市地下公路隧道,汽车类型主要为小汽车,所以取火灾的温升速率为200℃/ min。
(2)最高温度
对于城市地下公路隧道而言,隧道的衬砌结构内部温度的大小直接影响到衬砌结构本身的性能,所以说,最高温度的选取,是隧道内衬砌结构的防火设计的关键步骤。火灾最高温度同样主要取决于燃烧的车辆类型,对以小汽车为主要交通车辆的城市地下公路隧道,可认为其火灾中达到的最高温度为600℃。
(3)火灾持续时间
所谓火灾持续时间,就是从发生火灾开始,一直到火势被很好地控制结束所持续的时间。通过对隧道火灾进行大量的分析以及参考标准的火灾曲线,把2h作为隧道火灾的一个标准持续时间。
隧道衬砌结构内部温度场分布的确定
解析法计算衬砌结构内部的温度场
衬砌结构的热传导分析
当隧道内有火灾发生时,隧道结构周围的空气被迅速加热形成热气流层,气流层的温度不断升高,导致结构表面因被加热而使得表面温度迅速升高。由于结构的导热作用,热量则会传导至隧道衬砌结构的内部形成不均匀的温度场,而且衬砌结构内部的温度场是一个动态的温度场。
综上所述,可通过建立相应的热传导方程的方法来求解衬砌结构的导热问题。不考虑隧道衬砌结构本身的发热因素,同时考虑到衬砌结构的导热一般只是沿衬砌厚度方向进行,所以可得到衬砌结构的瞬态导热微分方程式为:

式中,λ(T)— 混凝土的导热系数,W/(m·K);
T — 衬砌结构内任意点的温度,K;
ρ(T)— 衬砌结构混凝土的密度,kg/m3;
c (T)— 衬砌结构混凝土的比热容,J/(kg·K);
t — 时间,s。
材料的热工性能的确定
由式(1)可以看出,衬砌结构的热工参数包括导热系数λc、比热容cc以及密度ρc。衬砌结构的材料主要是混凝土,由于混凝土具有较强的热惰性,所以说在火灾状况下的热工参数均是以温度为自变量的函数。
混凝土的导热系数与温度呈负相关性。为了简化计算,根据设计规程Eurocode 2可对混凝土的导热系数进行如下表示:
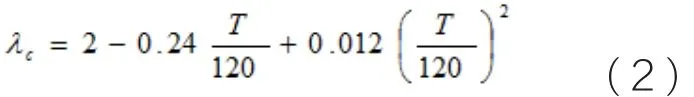
式中,20℃≤T≤1200℃
混凝土的比热容与温度有关且呈正相关性。因此,混凝土的比热容大致在800~1400 J/(kg·K)间变化。按照Eurocode 2的设计规程的规定,混凝土的比热容的计算供热如下:

式中,20℃≤T≤1200℃
混凝土的密度与温度的关系是负相关性。邵军等则按照法国所实施的相关规范,给出了衬砌结构混凝土的密度表达式:

隧道内衬砌结构内表面与热烟气以空气之间存有换热作用,而且受烟气流的流动的影响,换热过程并不稳定。对现有文献中的综合系数的取值进行整理后可以得出,现今普遍采用的综合换热系数的值如表1所示。

表1 综合换热系数h
结构的初始条件和边界条件的确定
初始条件以及边界条件的确定也是求解导热微分方程的关键。初始条件的确定相对来说较为容易,在火灾发生的那一瞬间,衬砌结构处在温度稳定的环境中,所以可假设衬砌结构的温度就是环境温度且是稳定的。故初始条件为:

由于衬砌结构的内侧是与火源接触的一侧,所以说衬砌结构的内侧是第三类边界条件,可表示为式(6)。假设隧道衬砌结构的外侧与岩土之间不存在接触热阻,也就是说是第一类边界条件,表示为(7)式。

式中,Tf—隧道内热烟气流的温度,K;
T0— 衬砌结构的初始温度,K;
h—混凝土与热烟气流间的对流换热系数,W/ (m2·K);
TS— 衬砌外侧岩土体的温度,K。
导热微分方程的计算及结果分析

图1 衬砌结构的内部温度值
为求解上述微分方程,假设混凝土的热工参数λ,c 和ρ以及衬砌结构与热烟气流的对流换热系数都是常数。对于第三类边界条件,上述导热微分方程(1)及第三类边界条件(6)可通过拉式变换进行求解,得到的温度分布为:
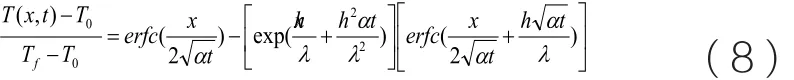

表2 误差函数选摘
选取城市地下道路隧道的内部衬砌结构的厚度为350mm。如此一来,就可由以上条件求得火灾时城市地下公路隧道的衬砌结构内部的温度分布情况,如图1所示,各条曲线为混凝土构件内不同深度处温度随时间的变化曲线。
由此对结果进行分析可得:
(1)在火灾发生后,隧道内的衬砌结构具有较大的温升速率,然而,衬砌结构内部的温度虽然同样升高但却有着较大的滞后性,而且衬砌内部温度低于表面温度。究其原因,这是由于混凝土具有比较小的导热系数,热量传递相对较慢,所以说,衬砌结构的内表温度具有很大的温度梯度,且温度分布极不均匀。
(2)由图1可看到,混凝土表面温度在30min内就达到了300℃以上(对于混凝土结构,认为小于300℃是安全的),事实上,对于实际的城市地下道路隧道而言,火灾的持续时间要在一个半小时以上,隧道内部的衬砌结构的表面温度更是高达400℃。所以说,考虑到衬砌结构的安全性能,必须要在衬砌结构上做些防火隔热措施。

图2 衬砌结构内部温度值随时间变化曲线

图3 表面处温度分布比较

图4 0.05m处温度分布比较
ANSYS模拟研究
为了与上述解析方法计算得到的温度场分布结果进行对比,本文利用ANSYS10.0程序对上述问题记性数值模拟,本次模拟模拟了2h后,不同深度0cm,5cm,10cm,15cm,20cm,25cm,30cm,35cm处温度随时间变化情况。模拟的结果如图2所示。
计算值、模拟值和实验值的对比分析
利用解析方法和ANSYS程序模拟得到城市地下公路隧道衬砌结构温度分布然后与现有的一些实验结果进行对比,如图3、图4所示,其中,红色曲线为排除水分对混凝土温度分布影响后得到的曲线。
对以上对比结果进行分析得到以下结论:
(1)在混凝土表面处,模拟值曲线温度略高于实验值,而且计算曲线开始阶段(5min内)与模拟值吻合较好,而随后有较大差异,其原因是在进行理论计算过程中进行了一些简化,而且认为混凝土材料的热物性参数为一个定值,而实际上其参数是受温度影响较大的。但值得注意的是,两模型具有相同的温度变化规律,这就说明计算所选取的模型是准确的。
(2)在距混凝土表面0.05m深处,实验结果整体上略小于模拟结果,这可归因于两方面因素:第一,实际混凝土构件内水分蒸发吸收部分热量,影响温度随时间变化所致;第二,数值模拟采用的简化理论模型和求解过程的思想导致了模拟结果与实际情况之间不可避免地存在一定差异。然而,从图中两条曲线的对比来看,模拟结果与实验结果还是较为吻合,因此,实验值同样可以验证模拟结果的准确性。
而在混凝土构件内部,理论计算值明显小于实验值,产生这种结果的原因一方面与在计算过程中对理论模型和求解过程的简化有关,另外很重要的一个原因仍然在材料热物性参数取值中,所采取的定性温度偏高所致。即计算过程中材料的热传递能力低于实际情况,导致分析解计算结果温度值低于实测值。
(3)从模拟值,分析解计算值和实验值的对比分析来看,采用数值计算方法的模拟计算值更加接近实际情况,计算结果的准确性较好。而采用解析解计算方法,由于无法避免材料热物性参数随温度变化而非定值对计算结果产生的较大影响,计算结果与实测值出入较大。
(4)分析图3和图4,可以看出随着混凝土内部深度的增加,计算结果与实验测试结果温升曲线的变化趋势是一致的,因此可以证明所选取的解析数学模型的准确性。
(5)三种方法得到的数据结果表明不同深度处温度差较大,易产生较大热应力,破坏结构的安全性和稳定性,因此可以得到结论,在城市地下公路隧道内对混凝土衬砌结构施加防火保护是十分必要的。
结语
本文运用解析法计算了火灾时城市地下道路隧道内衬砌结构的温度场,通过采用数值模拟以及实验值对比的方式验证分析了计算公式的准确性,以及衬砌结构的温度场分布规律。研究成果表明:1)火灾情况下,衬砌结构具有较大的温升速率,衬砌结构的温度会迅速到达其耐火极限,并且过高的温度会严重影响结构的安全性能。2)混凝土的热惰性会使衬砌结构在高温时在表面及内部产生较大的温度梯度,破坏衬砌结构的稳定。3)通过对温度场的计算及分析,结果表明,为了隧道内结构的稳定及安全,必须在衬砌结构上采取保护措施。
于 涛1,2李雪进2徐晨亮2李炎锋2杨 超2
1.中交公路规划设计院有限公司;
2.北京工业大学建筑工程学院
10.3969/j.issn.1001-8972.2016.11.001

