不同采样密度下县域森林碳储量仿真估计

郭含茹， 张茂震,*， 徐丽华， 袁振花， 秦立厚， 陈田阁

1 浙江农林大学 浙江省森林生态系统碳循环与固碳减排重点实验室，临安　311300　　2 浙江农林大学环境与资源学院，临安　311300　　3 濮阳市华龙区科学技术局，濮阳　457001



不同采样密度下县域森林碳储量仿真估计

郭含茹1,2， 张茂震1,2,*， 徐丽华1,2， 袁振花1,2， 秦立厚1,2， 陈田阁3

1 浙江农林大学 浙江省森林生态系统碳循环与固碳减排重点实验室，临安3113002 浙江农林大学环境与资源学院，临安3113003 濮阳市华龙区科学技术局，濮阳457001

采用浙江省台州市仙居县森林资源二类调查样地实测地上部分碳储量数据，结合Landsat TM影像数据，利用序列高斯协同仿真(SGCS)算法、序列高斯块协同仿真(SGBCS)算法，以4种地面采样密度(SD)SD1=0.012%、SD2=0.010%、SD3=0.007%、SD4=0.005%，估计全县森林碳储量及其空间分布，分析不同地面采样密度对区域森林碳储量及其分布格局估计精度的影响。结果表明：1)不同采样密度下SGCS和SGBCS估计的森林碳储量分布趋势相似，SGCS估计在采样密度为SD2时可以满足精度要求，且均值与实测最相符；SGBCS估计受采样密度影响较小，在四种采样密度下均可满足精度要求。2)SGCS、SGBCS估计的不确定性随着采样密度的降低均呈现出整体升高的趋势，增长速率在SD2采样密度时最低，相对SD1分别升高1.08%、-1.71%；当SGBCS算法的采样密度由SD2变为SD3时，样地数的减少对不确定性影响最大，但对区域空间变异格局估计没有实质性影响。3)将采样密度控制在SD2(0.010%) 水平，利用SGCS和SGBCS算法均能得到准确可靠的森林碳储量及其分布信息，同时能节省至少20%左右的森林调查工作量。

序列高斯协同仿真(SGCS)；序列高斯块协同仿真(SGBCS)；森林碳分布；空间变异；不确定性

固碳、减排是减缓全球气候变暖的两个同等重要的方面[1-2]。20世纪90年代后期特别是近年的研究均认为全球森林生态系统正起着CO2汇的作用[3-4]。《京都议定书》中将增加森林碳汇作为CO2减排的一个主要替代方式[5-8]。森林生物量、碳储量估计是森林碳汇计量的基础工作，也是评价森林对减缓全球气候变暖贡献的前提[6、9-10]。森林资源样地调查数据在相当长的时间内依然是最直接、最精确和最可靠的信息来源[11]。由于森林资源调查工作需要投入大量的人力、物力、财力，如何在保证精度的情况下，减少样地调查工作量，就需要对合理的采样密度(SD)进行分析，计算在一定的误差范围内应抽取的样本单元数[12-14]。

本研究采用浙江省台州市仙居县的森林资源二类调查样地实测地上部分碳储量数据，结合与样地尺度较为接近的30 m分辨率Landsat TM影像数据，利用序列高斯协同仿真算法(SGCS)、序列高斯块协同仿真算法(SGBCS)，在原始采样网格的基础上进行抽样，形成不同的采样密度，以探索采样密度对森林碳密度及其空间分布、空间变异格局的影响，并对估计结果的不确定性进行量化，以评价其精度。由于森林碳市场需要各种尺度规模的森林碳汇空间分布信息[15-18]，于是本研究将实验设计为两个尺度层面：1)采样密度对区域尺度碳空间分布信息估计结果的影响，利用SGCS算法实现，空间分辨率30m×30m；2)采样密度对森林碳分布空间估计尺度上推的影响，利用SGBCS算法实现，空间分辨率900m×900m。本研究作为一种对减少地面调查工作量的探索，为森林资源清查工作的展开提供参考。

1　材料与数据准备

1.1研究区概况

台州市仙居县(120°17′ 16″—120°55′ 51″ E，28°28′ 14″—28°59′ 48″ N)地处浙江省东南部(图1)，位于浙江第三大水系——椒江水系的源头，东西长63.6 km，南北宽57.3 km。全县总面积2013.18 km2。丘陵山地面积占总面积的80.6%，平原占11.1%。仙居县属浙东丘陵地带，山系盘桓，溪流切割，低山和丘陵占全县总面积的86.4%。地表分割强烈，河谷切割深邃，海拔范围742—1384.4 m。该县属典型亚热带季风气候，温暖湿润，四季分明，年平均气温17.2℃，年均降雨量1444 mm，年均蒸发量1190 mm，年平均日照时数1786 h。因区域地形、地貌影响，气候垂直分异规律明显。全县林业用地面积1.64583×105hm2。林业用地中，有林地1.53369×105hm2(其中竹林面积占6.73%)；灌木林地6.289×105hm2；未成林造林地2.579×103hm2；无立木林地1.889×103hm2；森林覆盖率77.9%；森林总蓄积5.555×106m3(2008年数据)。

图1　研究区位置和样地分布示意图Fig.1　Location of the study area and the plots distribution

1.2地面样地数据

文章所使用的森林资源数据来源于仙居县2008年森林资源二类调查中的抽样调查数据，共有样地307个。抽样总体为仙居县行政区范围，总体内样地按系统抽样方法进行布设，样地间距2 km×3 km，样地大小为28.28 m×28.28 m，面积0.08 hm2(图1)。野外样地测设由GPS定位，水平位置误差±(5—8) m。样地调查内容包括地貌、海拔、坡向、坡位、坡度、地类、林种、优势树种、平均年龄、平均胸径、平均树高等样地信息和树种、胸径等样木信息。样木起测胸径为5 cm。调查样木分为杉木、马尾松、硬阔、软阔4个树种组。利用浙江省单株立木生物量模型[19]计算地上部分生物量(表1)，求和得到各样地总的地上部分生物量，并根据生物量/碳储量转换系数和样地面积将地上部分生物量换算成碳密度(Mg/hm2)；表1中B表示单株立木生物量(kg)；D表示单株立木胸径(cm)；C表示样地碳密度(Mg/hm2)；i为样木号，j为样地号；0.5为IPCC提供的生物量/碳储量默认转换参数。以下森林碳储量均指单位面积森林地上部分碳储量，即森林碳密度。样地森林碳密度值(表2)介于0—87.005 Mg/hm2之间，平均值15.854 Mg/hm2，标准差16.747 Mg/hm2，变异系数达到1.056，属强变异类型。中位数为10.208 Mg/hm2(表2)，呈现出明显的负偏。

表1　研究区碳密度计算

表2　样本碳密度统计特征

1.3遥感影像数据

文章使用2007年10月仙居县全境Landsat TM影像数据，空间分辨率为30 m×30 m，与样地大小基本吻合。图像经几何校正和辐射校正处理，空间位置误差小于1个像元。利用软件Erdas 9.2提取307个样地所对应的遥感图像6个波段灰度值，即Band1、Band2、Band3、Band4、Band5、Band7。通过波段/波段组合计算得到原始波段、DVI (difference vegetation index)、RVI (ratio vegetation index)、NDVI (normalized difference vegetation index)、SAVI (soil-adjusted vegetation index)、CVI (conventional vegetation index)、EVI (enhanced vegetation index)等光谱值和样地调查数据(碳密度)之间的相关性。

2　研究方法

2.1采样密度设计

(1)

方程式(1)中，SD为采样密度，SN为样地数，A为研究区总面积201318 hm2，a为样地大小 0.08 hm2，A/a表示总体单元数。在保证数据各统计趋势相同的情况下，对原始采样网格进行抽样，依次随机选取样地数的100%、80%、60%、40%，形成4种不同的采样密度：SD1=0.012%、SD2=0.010%、SD3=0.007%、SD4=0.005%，如表2。样本碳密度的均值随着采样密度的降低大致保持不变，波动幅度小于0.3；中位数总体上呈现降低的趋势，相应的偏度、峰度、标准差、变异系数等统计量均有小幅度提升，与实际情况相符。

2.2区域尺度碳密度及其分布估计

从统计学角度去推断未采样位置可能取得结果的概率，或者得到估计值大于或小于某一阈值的概率，更符合地理研究的客观需要[20]，理论上所得到的观测值不是确定的，而应该是围绕一个特定的数学期望随机变化的正态分布函数。序列高斯协同仿真(sequential Gaussian co-simulation，SGCS)算法正是符合这一思想的随机模拟方法，它是一个基于图像的地统计条件模拟技术，以区域化变量理论为基础，通过量化随机函数的空间关系，得到其条件累积分布函数，随机产生服从该分布的一次模拟。地统计学中，半方差函数用来描述随机函数空间关系，相交的半方差函数可以度量两个随机函数相互的空间相关关系。设变量Z为森林碳储量，则Z(u)为定义在二维空间u处的随机函数，其半方差函数γZZ(h)、空间协方差CZZ(h)通过关于距离h的方程式进行计算：

(2)

(3)

式中,α是变程范围内第α个样本；相距h的两个样本称为一个样本对，N为变程范围内样本对的数量；为了区分样本对中的两个样本数据，分别称为头和尾，m-h和m+h分别为若干个样本对的尾和头数据的平均值。

协同遥感变量,选取与样地森林碳储量之间的相关系数最大的Band3，参与森林碳储量的仿真制图。设变量Y为遥感光谱变量，本研究中为Band3，则Y(u)为定义在二维空间u处的随机函数，那么两个随机函数——森林碳储量Z(u)和Band3Y(u)之间的交叉半方差函数γZY(h)和交叉协方差函数CZY(h)可计算为：

(4)

(5)

式中，mZ-h和mY+h分别为样本对中Z变量和Y变量的平均值。

位置u处的方差σ2(cs)借鉴协同克里格插值的方差计算方法：

(6)

(7)

(8)

概率密度函数积分得到其条件累积分布，并假定这个分布符合正态分布，该分布中的随机数作为待估位置u处的模拟实现。

SGCS算法的运行过程如下：

1)计算并拟合数据的半方差函数，确定该研究区的变程、块金值、基台值等参数；

2)随机选取一个待估位置u，计算以u为中心，变程范围内已知样本数据的均值、方差，确定条件累积分布函数，抽取随机数作为该位置的一次模拟实现；模拟值作为已知数据参加后续模拟；

3)根据随机路径依次访问各像元，由以该像元为中心的变程范围内的已知数据(包括之前的模拟值)重新建立条件累积分布函数，随机抽样，产生模拟值；

4)重复2、3步骤，直到所有像元都得到一个随机模拟值，完成该区域化变量在研究空间上的一次完整模拟实现；

(9)

SGCS算法保证了在变程范围内，模拟值加入已知数据集后仍符合原始的累积分布，方差不变。方法中的两处随机：1)随机选取第一个模拟位置并选用随机路径；2)在条件累积分布函数中随机抽取一个数作为模拟值。由于SGCS模拟过程中前一个随机模拟值被加入到下一次模拟条件中，所以选用随机路径可以最大程度降低随机误差的积累。若模拟依次进行，下一个位置的估计用到上一个位置的模拟值，随机误差被逐渐扩大。另外，搜索半径内由随机得到的点的个数设有上限，也是为了降低随机误差的逐渐扩大。第二处随机的本质是以概率统计理论方法为基础的一种计算方法，将抽样得到的随机数作为该问题的解。

2.3森林碳分布空间估计的尺度上推

大区域森林碳分布信息通常采用1km×1km或更低分辨率来表达，基于实测样地数据和遥感数据进行大区域森林碳分布制图，需通过尺度上推实现。序列高斯块协同仿真(SGBCS)由SGCS算法发展而来，用以实现尺度上推，输入高分辨率遥感影像和地面实测样地数据，可直接输出低分辨率的碳分布信息。将低分辨率的像元大小称为块，由m个高分辨率图像的像元组成，本研究块的大小为900 m×900 m(与1km区域尺度相近)，由30×30个分辨率为30 m×30 m的像元尺度上推得到。30×30个像元的均值、方差共同决定一个块的期望条件累积分布函数。利用方程式(7)计算均值；计算块内所有小像元估计值的方差σ2(bcs)(上标bcs是SGBCS的缩写)，必须考虑模拟值的空间自相关[17]：

(10)

式中，Cij是块内第i个像元与第j个像元的协方差。从该累积分布中，随机抽取一个值作为该块的模拟值；在此基础上SGBCS算法比SGCS算法又多进行一次随机模拟，即以待估块为中心，变程范围内的块作为样本，得到(基于块内像元模拟值的)块模拟值的累积分布函数，该累计分布函数的方差、均值按照方程式(6、7)计算得到，随机抽样实现一次块模拟。运行过程如2.1，直到计算出低分辨率像元(块)上的森林碳密度的样本均值图和相应的方差图、概率图，随机模拟200次，块估计值的计算与方程式(9)相同。

2.4验证方法

从碳密度估计值、碳密度分布趋势、不确定性(uncertainty，UC)、空间变异格局4个方面对比分析不同采样密度下样地尺度、区域尺度森林碳密度估计的差异，并检验采样密度对尺度上推的影响。

2.4.1不同采样密度的空间预测准确性

(11)

(12)

采用决定系数(R2)、均方根误差(RMSE)指标来评判不同采样密度下SGCS算法的估计精度，RMSE越小，估计精度越高。Z(u)mea是位置u处实测碳密度，SN为样本数。并且，本研究假定，以实测数据为参照，R2、RMSE升高或降低10%以内，为满足精度(Ac)要求范围:

(13)

式中，x=1,2,3；SD表示在不同采样密度下的R2或RMSE值或不确定性。

然而对于SGBCS碳密度分布估计图，并没有利用采样点来检验其估计精度，而是将30 m×30 m分辨率SGCS碳密度估计值视为真值，在900 m×900 m分辨率SGBCS碳密度分布图上随机选取300个点，使其大体均匀分布在整个研究区内，计算其与相应真值的R2、RMSE。另外，SGBCS实现了尺度上推，在已有的研究中，大多将尺度上推之后的影像与转换前的影像信息进行相关性比较，以检验尺度结果的可靠性。本研究通过随机选取的300个点SGCS、SGBCS估计值之间的相关性，来评价采样密度对尺度上推的影响。

2.4.2不确定性的量化及空间变异格局

Bourennane等[21]指出标准差(Std.Dev.)分布图可以用来评价在空间预测不确定性方面的表现，在保证空间预测准确性的同时，标准差越小，空间预测不确定性越小。本研究中SGCS、SGBCS算法最终以200次模拟值的均值作为估计值，200次模拟值的标准差即为估计过程中的不确定性量化值，在输出森林碳密度分布图的同时可获得估计值的标准差图。不确定性的变化速率q可用来判定降低采样密度对空间预测精度的影响程度：|q| 越大表示采样密度对不确定性影响越大。标准差与均值的比值称为变异系数(Var.coef.)，可以反映该位置的变异特征，本研究用变异系数图来体现空间变异格局。

(14)

式中，x=1,2,3；此处，SD表示在不同采样密度下的不确定性。

2.4.3逐像元对比

为了更加清晰、直观的对比不同采样密度下的空间预测结果，在研究区南北方向上做了一条横断线，条带的宽度与像元大小保持一致，使其尽量横跨所有典型的用地类型，提取此横断线上各像元的不确定性及空间变异特征。

3　结果与分析

3.1半方差函数拟合

本研究中针对同一研究区的不同采样密度样地数据进行半方差函数拟合时，采用相同的块金值、变程等参数，将随机变异控制在40%—60%之间，拟合的变程为5460 m。SGCS、SGBCS算法利用变程范围内已知的样地和光谱数据来预测待估位置碳密度值(图2)。

图2　半方差函数拟合曲线Fig.2　Semi-variance fitting curve

3.2碳密度及其分布估计

4种不同采样密度的实测样地数据结合Landsat TM影像Band3光谱数据，分别进行200次SGCS、SGBCS，得到分辨率为30 m × 30 m(图3)、900 m × 900 m的森林碳密度分布(图4)。

图3　序列文斯协同仿真算法(SGCS)森林碳密度估计图Fig.3　Sequential gaussian co-simulation (SGCS) forest carbon density estimate map

对比不同采样密度的SGCS、SGBCS结果发现：1)不同采样密度的森林碳分布估计结果具有相似的趋势，均为四周高、中心低，高值区域集中在研究区的西南部；中心低值区域的范围随着采样密度的降低有扩大趋势。2)若将四种采样密度的估计结果叠加进行对比还可以发现即使相对于整个研究区而言碳分布整体趋势相似，但仍存在细微差别，这与随机抽样选取的样地分布有关，采样位置的差异直接影响碳密度估计结果及其分布情况(图3,图4)。以研究区西南区域(图3-SD1中虚线范围内)为例，随着采样密度的降低，碳密度的估计结果受变程范围内已知样地影响的程度逐渐加剧，待估位置的属性值模仿已知位置的属性值，从而减弱了其所在区域的差异，使得原本低/高值位置受周围高/低值样地的影响被高/低估。这种现象在40%样地数的仿真结果中表现尤为明显。为了检验这种现象的产生是否完全归因于40%样地数的采样密度过低，在保证样地碳密度各统计特征相似的情况下，重新随机抽取了60%的样地数进行仿真，两次仿真的结果相差很大(图5)；由此可见，均匀的采样密度是得到可靠的分布信息的前提。

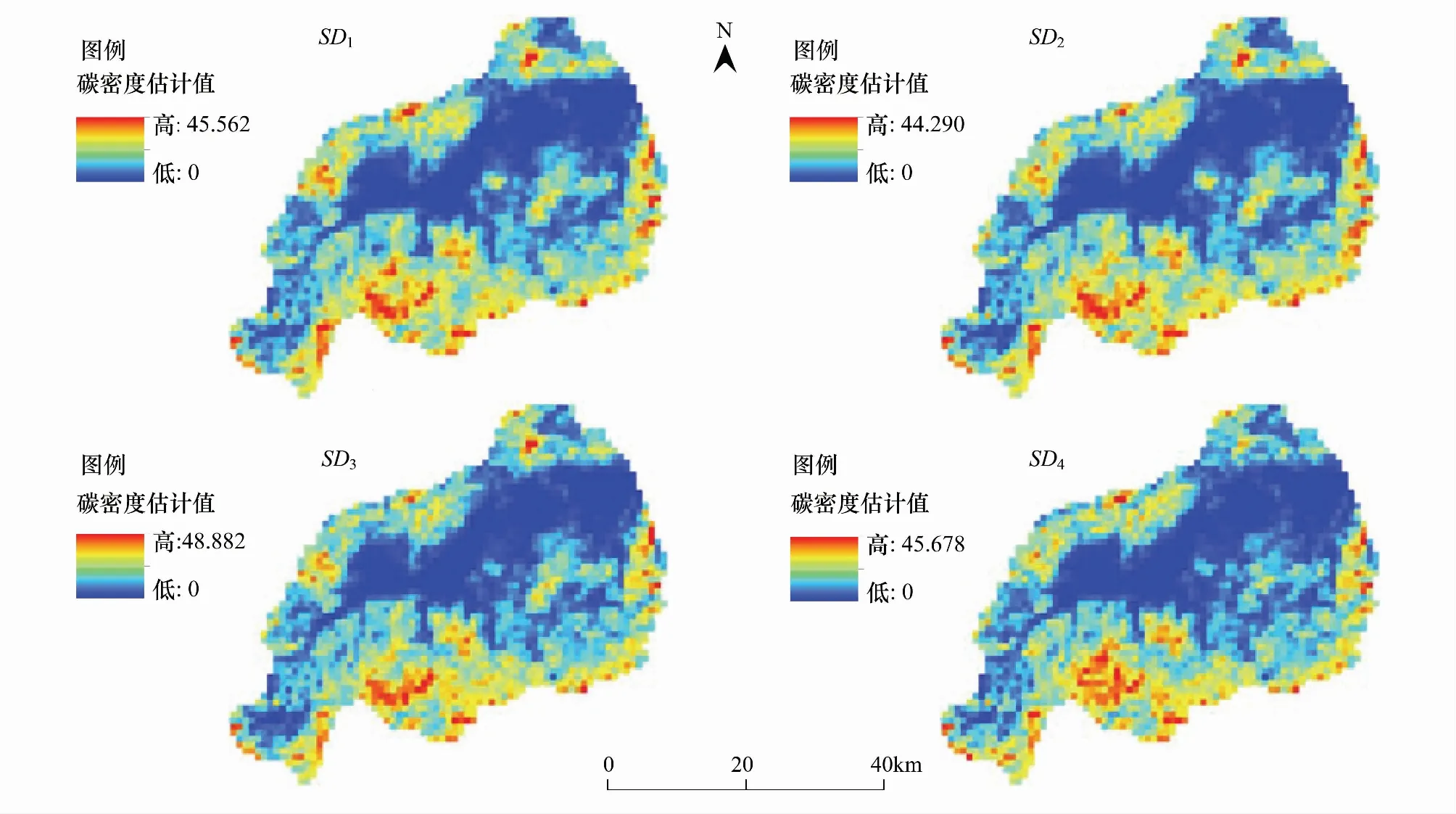
图4　序列高斯块协同仿真(SGBCS)森林碳密度估计图Fig.4　Sequential gaussian block co-simulation (SGBCS) forest carbon density estimate map

图5　不同采样密度的样地分布情况及对估计结果的影响Fig.5　Plots distribution in different sampling density and its influence on the estimated results

不同采样密度的碳密度SGCS估计，R2分别为0.666、0.634、0.600、0.576(P< 0.01)；以该结果作为真值，碳密度SGBCS估计的R2分别为0.871、0.867、0.857、0.853(P< 0.01)。可以认为基于SGBCS的尺度上推至少保留了SGCS碳密度估计结果的85%；随着采样密度的降低，SGCS结果与SGBCS结果之间相关性有减弱的趋势，但在采样密度降低了60%的情况下，相关性水平仅降低了0.018。随着采样密度的降低，R2减小，RMSE增大，估计精度呈降低趋势。如图6，SGCS算法的R2分别减小5.97%、10.45%、13.43%，RMSE分别增大7.36%、15.50%、23.32%；在SD2采样密度下满足精度要求。SGBCS算法的R2分别减小0.46%、1.61%、2.07%，RMSE分别增大1.79%、5.55%、9.30%；在4种采样密度下均可满足精度要求。可见，采样密度的降低对基于SGBCS算法尺度上推的影响较小，若使用SGBCS算法进行区域尺度碳密度估计，可适当降低对采样密度的要求；然而对SGCS碳密度估计的影响不可忽略，采样密度仅在SD2时可达到精度要求。

图6　不同采样密度的估计精度Fig.6　Estimate accuracy in different sampling density

3.3不确定性及空间变异格局

随着采样密度的降低，SGCS的不确定性有升高的趋势，分别为：0—23.09、0—23.34、0—23.89、0—24.63；且不确定性增长的速率逐渐增大，分别为1.08%、2.36%、3.10%，增长速率在采样密度=SD2时最低，SD3时为SD2时的2倍，SD4时增长速率最大，此时估计结果的不确定性增加了6.67%(图7)。不同采样密度的SGBCS不确定性差异较小，按照采样密度由大到小分别为0—14.61、0—14.36、0—14.71、0—14.86，不确定性最大值的波动幅度在0.5以内；随着采样密度的降低，SGBCS的不确定性先出现降低的趋势又回升至更高，变化速率分别为-1.71%、2.44%、1.02%，在采样密度=SD2时增长为负，不确定性达到最低，SD4时不确定性增长了1.71%(图7)。由此可见：四种采样密度对SGCS估计结果不确定性的影响均在精度要求范围内；对基于SGBCS算法的尺度上推不确定性的贡献不大，然而在采样密度由SD2变为SD3时，不确定性的增长速率急速上升，此时样地个数的减少对其影响程度最大。

图7　不同采样密度估计结果的不确定性Fig.7　The uncertainty of the estimation in different sampling density

按照采样密度由大到小，SGCS结果的变异系数分别为：0—14.078、0—14.081、0—14.084、0—14.073；SGBCS结果的变异系数分别为：0—13.826、0—13.881、0—14.004、0—13.573。由此可见：基于SGCS、SGBCS算法的森林碳密度估计，其空间变异格局几乎不受采样密度的影响。

以上结果足以表明：在可控的误差范围内，适当降低采样密度，利用SGCS、SGBCS算法，可以得到准确可靠的不同尺度森林碳密度及其空间分布信息。SGCS、SGBCS的森林碳密度估计值均在SD3采样密度时达到最高70.635Mg/hm2、48.882 Mg/hm2；SGCS的不确定性在SD2时增加速率最小，SGBCS的不确定性在SD2时达到最低，由SD2变为SD3时样地个数的减少对不确定性影响程度最大；不同采样密度下SGCS、SGBCS的森林碳密度空间变异格局均保持在相当水平；由此可推断：采样密度在SD2、SD3之间一定存在一个最优值，使SGCS、SGBCS估计精度可靠的同时不确定性维持在一个较低水平，这个最优的采样密度仍需进一步深入探索。

3.4逐像元对比

逐像元提取横断线上各像元的不确定性及空间变异特征，由北至南依次排序，同一位置处不同采样密度、不同尺度进行对比(图8)。结果表明：1)SGCS、SGBCS结果的趋势一致，剧烈的空间变异发生在碳密度及其不确定性较低的区域，尺度上推后碳密度空间变异程度减弱，但变异对比度加剧。各采样密度的空间变异特征吻合度比不确定性的更高，表明空间变异格局的估计受采样密度的影响相对较小。2)对比同一位置处不同采样密度的不确定性，可以发现，SD1、SD2吻合度较好，且比SD3、SD4两种采样密度时估计不确定性小；但图8中虚线环范围内的像元例外，可能是由于处于林地与城镇居民聚集区交汇的位置，出现异常现象。城镇居民聚集区碳密度几乎为零，若碳密度为零，则运算过程中会对分母做非零处理，于是会出现该位置不确定性很小而变异系数很大的情况。

图8　不同采样密度SGCS、SGBCS不确定性及空间变异特征Fig.8　Uncertainty and spatial variability in different sampling density

4　结论

(1)不同采样密度下基于SGCS和SGBCS的森林碳分布图基本格局相似。随着采样密度的降低，基于SGCS算法的森林碳密度值的估计范围有增大的趋势，在本研究的4种采样密度下，采样密度为SD3时，碳密度估计值范围0—70.635Mg/hm2，与实测碳密度范围最为接近，其次是SD4时0—69.485 Mg/hm2，但两种采样密度的估计结果均不能满足精度要求；SD2采样密度下的碳密度估计值达到精度要求，其碳密度估计范围为0—67.485Mg/hm2，且均值为15.425 Mg/hm2，与实测碳密度平均值15.854 Mg/hm2最相符。SGBCS估计受采样密度影响较小，在4种采样密度下均可满足精度要求，采样密度的降低对基于SGBCS算法尺度上推没有实质性影响。

(2)SGCS、SGBCS估计的不确定性随着采样密度的降低均呈现出整体升高的趋势，增长速率在SD2采样密度时最低，相对SD1分别升高1.08%、-1.71%；基于SGBCS算法的尺度上推不确定性受采样密度的影响较小，然而在采样密度由SD2变为SD3时，不确定性的增长速率急速上升，样地数的减少对不确定性影响最大。采样密度的降低均对区域空间变异格局估计没有实质性影响。

(3)利用SGCS、SGBCS和森林资源清查样地进行森林碳储量及其分布估计，可以适当降低对采样密度的要求。本研究区试验表明，在现有二类调查水平上减少20%的样地数仍能保证数据精度，得到准确可靠的仙居县县域森林碳储量及其分布信息。但对样地的选取与分布要求较高，需要考虑选择各种覆盖类型，且样地的布设要相对均匀。

5　讨论

目前区域森林植被碳储量估计研究领域面临着两大挑战：(1)如何精准地量化森林植被碳的空间格局和分布，以及从点测量尺度上推到更大的国家、区域和全球尺度上[16]。(2) 由于存在数据不准确、方法不得当以及对碳、植物、土壤三者之间的生理过程和关系的理解的差距，从而使森林碳汇的估计存在不确定性[16]。因此，对碳的管理和决策的质量高低是受森林碳估计中包含的不确定性影响的，所以迫切需要去提高估测技术、数据质量和最终的森林碳估计图的质量。

近年来，仿真算法在反映局部特征、再现森林碳分布信息以及量化不确定性等方面的独特优势已被大量研究证实：2004年，冯益明、唐守正等应用序列指示条件模拟算法模拟森林类型空间分布，指出该方法可以作为获得森林类型分布图的有效途径[22]；2011年，沈希等采用一元二次非线性回归和序列高斯协同仿真算法分别模拟森林地上部分碳密度及其分布，表明序列高斯协同仿真较一元二次非线性回归在估计区域森林碳空间分布上有明显优势[23]；Wang和Zhang 等人进一步发展了基于协同仿真算法的尺度上推森林碳制图的方法——块协同仿真算法(SGBCS)[16-17、24]，并建立了不确定性从输入数据到输出结果的一个传播模型。本研究在前人基础上运用序列高斯协同仿真(SGCS)、序列高斯块协同仿真(SGBCS)算法分析了采样密度对县域森林植被地上部分碳储量估计及尺度上推的影响。

目前大量针对森林碳储量估计的研究只在某一采样密度下进行，对不同采样密度下森林碳储量估计精度的研究极少有报道。通常认为，在较大的采样密度下，误差较小[25-27]；然而地面样地调查工作劳动强度大、成本高、周期长，一味增大采样密度从经济学角度考虑是不可取的。且谢邦昌[28]曾指出，随着采样密度的增加，抽样误差随之减小，但在一定阶段后，趋于稳定；非抽样误差随之增大；该研究结果表明，一味增大采样密度并不会使总体误差持续减小。所以一定存在某一合适的采样密度，可以在满足精度要求的同时降低投入的成本。2014年张茂震等人[29]证实，无论是全部样地还是减少一半的样地，利用SGCS算法估计的森林碳储量总体均值均在抽样估计置信区间以内；且一半样地数得到的成本效益优于使用全部样地的结果，但究竟使用多少样地使得成本效益最优，文中并未给出明确的结论。本研究对其研究结果进一步深化，尝试4种不同采样密度的SGCS、SGBCS算法的碳密度估计，从碳密度取值范围、空间分布、不确定性、空间变异等方面评价了采样密度对估计精度的影响，最终得出结论：在现有二类调查水平上减少20%的样地数仍能保证数据精度，得到准确可靠的仙居县县域森林碳储量及其分布信息。

文章中仍存在以下几点不全面的地方：

(1) 在包括样地实测、生物量经验模型估算、遥感影像协同变量选取、仿真估计等一系列生物量/碳储量估计过程中，任何一个环节都存在不同程度的不确定性，这些不确定性或累加，或抵消或产生复杂的相互作用，这都是目前不确定性研究领域所未能探明的问题，也是学者们关心的研究热点。本文所涉及到的仅仅是仿真估计过程中的这部分不确定性，以此来评价降低采样密度对仿真估计精度的影响，由于研究条件限制，未能对上述各部分的不确定性进行阐明分析。

(2) 文中结果表明，SGCS、SGBCS的估计结果，在SD2、SD3之间均发生剧烈的变化，可以推断采样密度在SD2、SD3之间一定还存在一个最优值，这个最优的采样密度仍需进一步深入研究。另外，针对本研究区来说，降低采样密度可以得到较好的仿真/块仿真结果的原因可能是研究区空间一致性较好，对于其他地形地貌类型的研究区，甚至更大区域，降低采样密度是否同样能有较好的结果仍需进一步探索。

(3) 本研究以随机抽样的方式降低采样密度，容易造成样地分布不均匀，若能结合样地属性抽取样地，如结合不同地类所占面积比例进行系统抽样，可能会取得更好的估计结果。

[1]冯朝元. 森林碳汇与区域森林保护. 湖北林业科技, 2012, 174: 42-48.

[2]鲁丰先, 张艳, 秦耀辰, 陈真玲, 王光辉. 中国省级区域碳源汇空间格局研究. 地理科学进展, 2013, 32(12): 1751-1759.

[3]Keeling C D, Chin J E S, Whorf T P. Increased activity of northern vegetation inferred from atmospheric CO2measurements. Nature, 1996, 382: 146-149.

[4]方精云, 朴世龙, 赵淑清. CO2失汇与北半球中高纬度陆地生态系统的碳汇. 植物生态学报, 2001, 25(5): 594-602.

[5]吕景辉, 任天忠, 闫德仁. 国内森林碳汇研究概述. 内蒙古林业科技, 2008, 34(2): 43-47.

[6]周隽, 王志强, 朱臻. 全球气候变化与森林碳汇研究概述. 陕西林业科技, 2011, (2): 47-52.

[7]何英, 张小全, 刘云仙. 中国森林碳汇交易市场现状与潜力. 林业科学, 2007, 43(7): 106-111.

[8]谢本山, 李峰, 王涛. 森林碳汇在低碳经济中的作用. 现代农业科技, 2010, 23: 205-506.

[9]李顺龙. 森林碳汇经济问题研究. 哈尔滨: 东北林业大学[D], 2005.

[10]续珊珊, 姚顺波. 森林碳汇研究进展. 林业调查规划, 2011, 36(6): 21-25.

[11]刘安兴. 浙江省森林资源动态监测体系方案. 浙江林学院学报, 2005, 22(4): 449-453.

[12]陈光, 贺立源, 詹向雯. 耕地养分空间差值技术与合理采样密度的比较研究. 土壤通报, 2008, 39(5): 1007-1011.

[13]吕康梅, 张一鸣, 于涛. 北京市森林资源固定样地调查体系研究. 林业资源管理, 2009, (2): 43-48.

[14]罗仙仙. 森林资源综合监测相关抽样技术理论与应用研究[D]. 北京: 北京林业大学, 2010.

[15]刘畅, 李凤日, 贾炜玮, 甄贞. 基于局域统计量的黑龙江省多尺度森林碳储量空间分布变化. 2014, 25(9): 2493-2500.

[16]Wang G X, Oyana T, Zhang M Z, Adu-Prah A, Zeng S Q, Lin H, Se J Y. Mapping and spatial uncertainty analysis of forest vegetation carbon by combining national forest inventory data and satellite images. Forest Ecology and Management, 2009, 258: 1275-1283.

[17]张茂震,王广兴,周国模,葛宏立,徐丽华,周元中. 基于森林资源清查、卫星影像数据与随机协同模拟尺度转换方法的森林碳制图. 生态学报, 2009, 29(6): 2919-2928.

[18]张维成, 田佳, 王冬梅, 丁国栋, 孟东霞. 基于全球气候变化谈判的森林碳汇研究. 林业调查规划, 2007, 36(5): 18-22.

[19] 沈楚楚. 浙江省主要树种(组)生物量转换因子研究[D]. 临安: 浙江农林大学, 2013.

[20] 赵彦锋, 孙志英, 陈杰. Kriging插值和序贯高斯条件模拟算法的对比分析. 地球信息科学学报, 2010, 12(6): 767-776.

[21]Bourennane H, King D, Couturier A, Nicoullaud B, Mary B, Richard G. Uncertainty assessment of soil water content spatial patterns using geostatistical simulations: an empirical comparison of a simulation accounting for single attribute and a simulation accounting for secondary information. Ecological Modeling, 2007, 205(3): 323-335.

[22]冯益明, 唐守正, 李增元. 应用序列指示条件模拟算法模拟森林类型空间分布. 生态学报, 2004,24(5):946-952.

[23]沈希, 张茂震, 祁祥斌. 基于回归与随机模拟的区域森林碳分布估计方法比较. 林业科学, 2011,47(6):1-8.

[24]Wang G X, Zhang M Z, Gertner G Z, Oyana T, McRoberts R E, Ge H L. Uncertainties of mapping aboveground forest carbon due to plot locations using national forest inventory plot and remotely sensed data. Scandinavian Journal of Forest Research, 2011: 1-14.

[25]陈光, 贺立源, 詹向雯. 耕地养分空间差值技术与合理采样密度的比较研究. 土壤通报, 2008, 39(5): 1007-1011.

[26]魏士忠, 窦宏海, 刘学东, 李艳春. 立木调查中样地的面积、数量与抽样精度的关系. 河北林果研究, 2013, 28(1): 41-43.

[27]Mueller T G, Pierce F J. Soil carbon maps: Enhancing spatial estimates with simple terrain attributes at multiple scales. Soil Sci. Soc. Am. J., 2003, 67 (1): 258-267.

[28]谢邦昌(原著). 张尧庭，董麓(改编). 抽样调查的理论及其应用方法. 北京: 中国统计出版社, 1998: 1-11.

[29]张茂震, 王广兴, 葛宏立, 徐丽华. 基于空间仿真的仙居县森林碳分布估算. 林业科学, 2014, 50(11): 13-22.

Simulation of regional forest carbon storage under different sampling densities

GUO Hanru1,2, ZHANG Maozhen1,2,*, XU Lihua1,2, YUAN Zhenhua1,2, QIN Lihou1,2,CHEN Tiange3

1ZhejiangProvincialKeyLaboratoryofCarbonCyclinginForestEcosystemsandCarbonSequestration,ZhejiangAgricultureandForestryUniversity,Lin′an311300,China2SchoolofEnvironmental&ResourceSciences,ZhejiangAgricultureandForestryUniversity,Lin′an311300,China3HualongDistrictScience&TechnologyBureauofPuyang,Puyang457001,China

Forest inventory data still represent the most direct, accurate and reliable source of information over a long period. Given the substantial labor, material and finances required, we need a reasonable sampling density (SD) to reduce the workload of field investigation.SDis a key issue on the accuracy and cost of estimation. A minimum number of sample plots given certain accuracy requirements is the most economical solution for spatial estimation of forest carbon. At present, most research on forest carbon storage is only valid for a particularSD. Studies of estimation accuracy at different sampling densities are rare. Generally, the greater theSD, the smaller the error. However, blindly increasingSDis not desirable and does not continuously reduce total error.

This study is based on Forest Management Inventory-measured aboveground carbon storage data of Xianju County for Taizhou (Zhejiang Province), and Landsat Thematic Mapper imagery of 30 m × 30 m resolution. Using sequential Gaussian co-simulation (SGCS) and sequential Gaussian block co-simulation (SGBCS) algorithms, a geostatistical image-based conditional simulation technique was used to map and analyze uncertainty of natural resources and environmental systems during recent years. We explored the effect ofSDon forest carbon and its spatial distribution estimates, uncertainties, and spatial variability at fourSDlevels, i.e.,SD1=100%,SD2=80%,SD3=60%, andSD4=40% of total plots. Because the international forest carbon market needs various scales of spatial distribution, we designed two scale levels: 1) the impact of differentSDson the spatial distribution of carbon estimation at regional scale, using the SGCS algorithm with spatial resolution 30 m × 30 m; and 2) the impact of differentSDson upscaling for regional forest carbon estimation, using the SGBCS algorithm with spatial resolution 900 m × 900 m. This study is an attempt to reduce the investigation workload and provides a reference for implementation of a forest resource inventory.

The results show the following. 1) Under differentSDs, SGCS and SGBCS had the same distribution trends in estimation of forest carbon density. SGCS estimation was able to meet accuracy requirements when forSD2, carbon density was 0—67.485 Mg/hm2with mean 15.425 Mg/hm2, consistent with the measurement. SGBCS carbon density estimation was less influenced bySD, allSDscould meet the accuracy requirements, and a smallerSDhad no substantial impact on upscaling. 2) Uncertainty of the SGCS and SGBCS estimation had overall rising trends, and the increase rate was smallest forSD2. ForSD1, uncertainty of SGCS and SGBCS estimation increased by 1.08% and decreased by -1.71%, respectively. Uncertainty of carbon density estimation by SGBCS was less influenced bySD. WhenSDwas changed fromSD2toSD3, it reduced the plot number, resulting in the greatest impact on uncertainty of SGBCS estimation.SDhad less contribution to estimation of the spatial variability. 3) Estimation of forest carbon storage and its distribution with the SGCS/SGCBS algorithms could reduce the requirement ofSDappropriately. Not only were we able to obtain reliable estimation information, but we could also reduce the workload of the forest survey by at least 20% forSDat theSD2level (about 0.010% of total regional area).

sequential Gaussian co-simulation (SGCS); sequential Gaussian block co-simulation (SGBCS); forest carbon distribution; spatial variability; uncertainty

国家自然科学基金项目(30972360, 41201563)；浙江省林业碳汇与计量创新团队项目(2012R10030-01)

2014-12-27; 网络出版日期:2015-10-30

Corresponding author.E-mail: zhangmaozhen@163.com

10.5846/stxb201412272587

郭含茹, 张茂震, 徐丽华, 袁振花, 秦立厚, 陈田阁.不同采样密度下县域森林碳储量仿真估计.生态学报,2016,36(14):4373-4385.

Guo H R, Zhang M Z, Xu L H, Yuan Z H, Qin L H, Chen T G.Simulation of regional forest carbon storage under different sampling densities.Acta Ecologica Sinica,2016,36(14):4373-4385.