庐山重力短基线场初值测定
邢乐林 王林海 孙少安 玄松柏 汪 健 谈洪波
1 中国地震局地震研究所(地震大地测量重点实验室),武汉市洪山侧路40号,430071 2 中国地震局地壳应力研究所武汉科技创新基地,武汉市洪山侧路40号,430071
庐山重力短基线场初值测定
邢乐林1,2王林海1,2孙少安1,2玄松柏1,2汪健1,2谈洪波1,2
1中国地震局地震研究所(地震大地测量重点实验室),武汉市洪山侧路40号,430071 2中国地震局地壳应力研究所武汉科技创新基地,武汉市洪山侧路40号,430071
利用FG5绝对重力仪对庐山基线场的3个基点和九江地震台的1个基准点进行绝对重力测定,使用7台CG-5相对重力仪对24个基点和1个基准点进行2个往返闭合测量。基于绝对重力控制解算的结果表明,基点点值精度均优于±5.0 μGal,相邻各段段差精度均优于±3.0 μGal。该基线场初值测定方法是一种崭新和现代的方法,具有科学意义和经济效益。
基线场;标定;绝对重力测量;相对重力测量
随着绝对重力观测技术的发展,绝对重力控制下的相对重力联测解算为基线场的初值测定提供了一条崭新的途径。始建于1985年的庐山重力短基线场由24个基点沿庐山北山公路布设而成[1-3],部分测点(1、2、7、10、13和21)目前已遭严重破坏,需进行升级改造。2011年,中国地震局地震研究所联合陕西省地矿局第二综合物探大队对其进行踏勘和选埋。本文尝试联合FG5绝对重力仪与CG-5相对重力仪对庐山短基线场进行初值测定。结果表明,基线场各基点点值精度均优于±5.0 μGal。
1 测量概况
庐山短基线场位于九江市庐山风景区,由24个基点和4个绝对点构成,如图1所示。庐山位于长江南岸,东临鄱阳湖,广布湖泊、河流、峰峦与坡地,地貌特征呈现多样化,为断块结构。
2015-01-07~12中国地震局地震研究所使用7台CG-5相对重力仪(SN:207、217、221、231、511、834和845)和1套FG5绝对重力仪(SN:232)对庐山短基线场进行测量。其中4个绝对点(引点位于九江地震台,其他3个位于基点)利用FG5绝对重力仪进行绝对重力测定,同时利用2台CG-5相对重力仪进行重力垂直梯度测定,以便将绝对重力值归算至地面,为相对重力联测提供起算基准;相对重力联测则利用7台CG-5相对重力仪,对24个基点进行2个往返闭合测量。
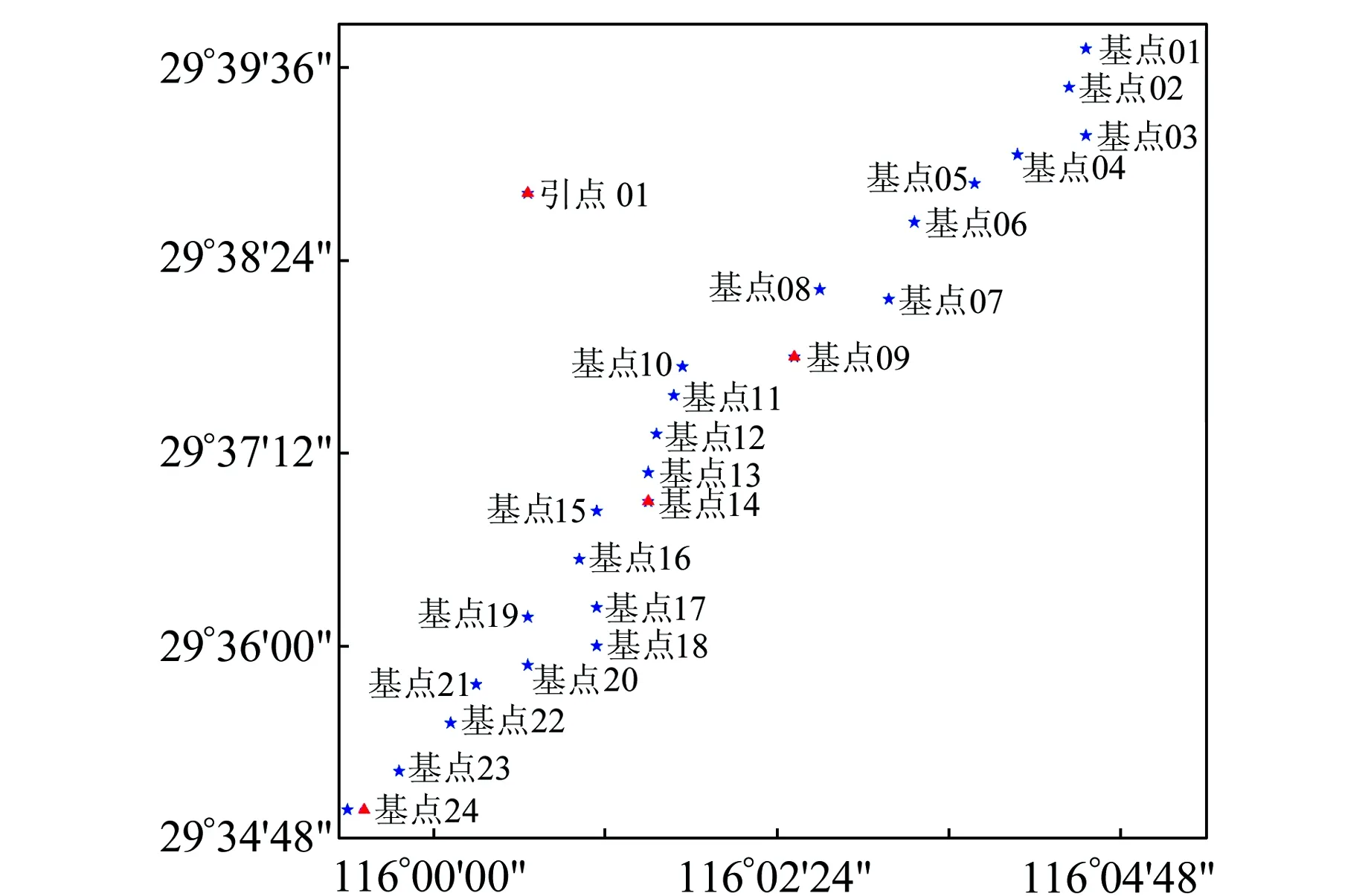
图1 庐山基线场测点分布Fig.1 The distribution of the stations at Lushan gravimeter scale calibration field
2 数据处理及结果
FG5绝对重力仪的标称精度优于5 μGal,且不同仪器之间的较差为1~2 μGal,不存在明显的系统偏差[4-5]。使用FG5绝对重力仪进行4个点的绝对重力测量,每次观测至少25 h,每h测量1组,每组100次下落,每台仪器在每个测站的有效落体数不少于2 400次,各组重力值标准差要求优于±5 μGal。利用2台CG-5相对重力仪进行重力垂直梯度测量。为保证测量结果的精度,在每个测站上地面与130 cm高度处至少进行5个高-低-高或低-高-低的往返闭合测量。
为了得到高精度的地面绝对重力值,利用g9绝对重力测量数据处理软件对加速度进行改正,包括大气压力、极移、梯度归算和潮汐等改正,结果见表1。
重力网平差中,绝对点观测结果以5.0 μGal精度定权;相对重力联测由于各台CG-5重力仪的性能和精度不一致,观测值的权重按仪器观测资料确定。对各台仪器联测观测值的权以15.0 μGal精度定权,根据试算结果定出其后验中误差mN0,以此精度重新定权作整体平差,进行2~3次迭代后可获得精度趋于稳定的结果。平差后各基点重力值、段差及其精度见表2。

表1 绝对点重力值
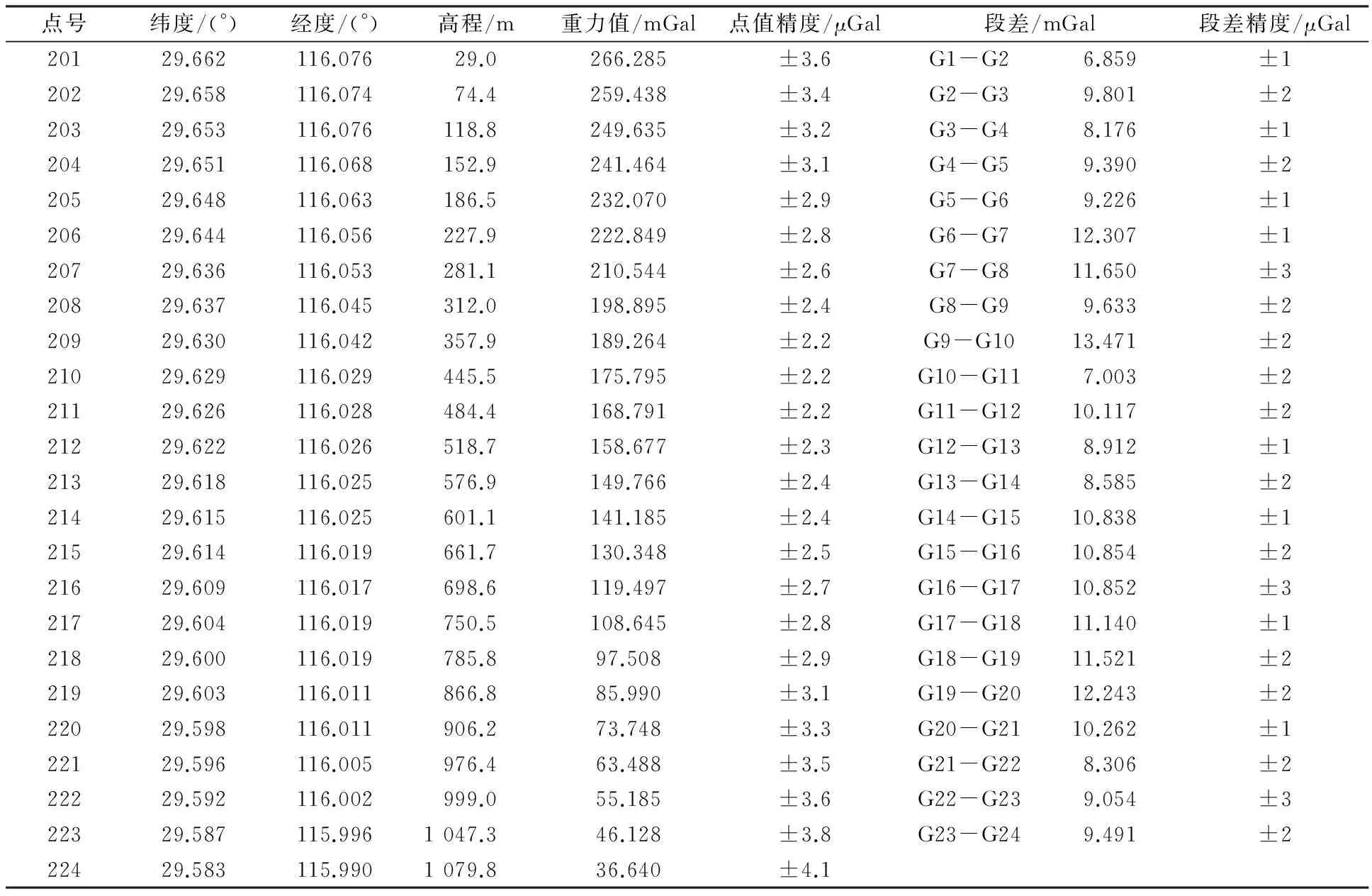
表2 庐山基线场各测站重力值及相邻测站间重力段差结果
3 结果比较与分析
3.1结果比较
由表2可见,平差后24个基点的重力值精度均优于±5.0 μGal,平均精度为±3.0 μGal;各测段段差精度均优于±3.0 μGal,优于设计精度±5.0 μGal。2000联测与本次观测结果的比较见表3和图2。13个测段中,绝对值最大变化为40.0 μGal,最小为4.0 μGal,平均为18.8 μGal,其中10个测段的变化值均在±20.0 μGal范围内。尽管庐山短基线场地质条件稳定,但存在一定的构造运动、地球物理事件(如2005-11-26九江MS5.7地震)以及基点附近的地形、地物变化等,均会引起重力变化。
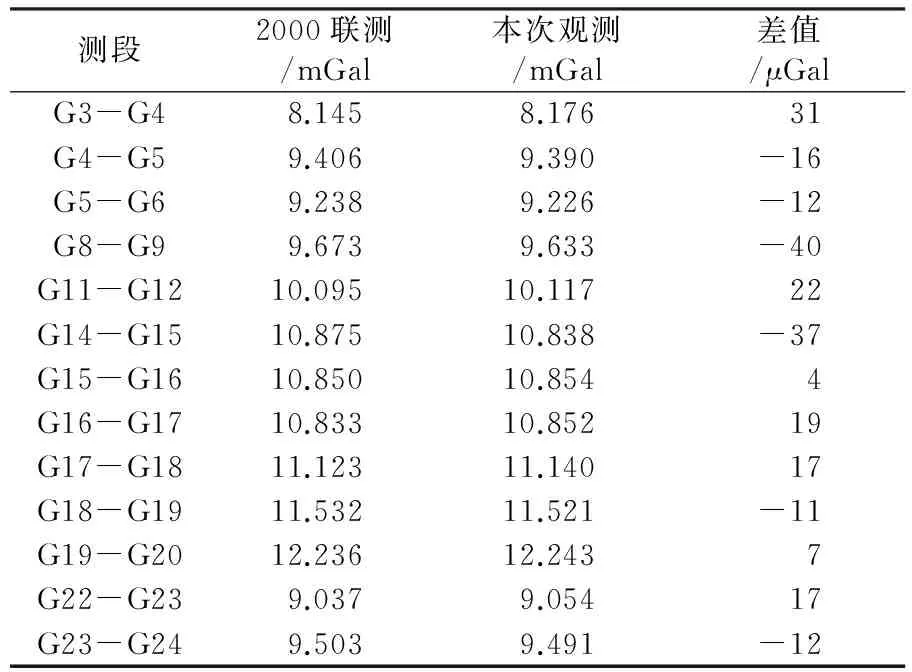
表3 庐山基线场相邻测站间重力段差观测结果的比较
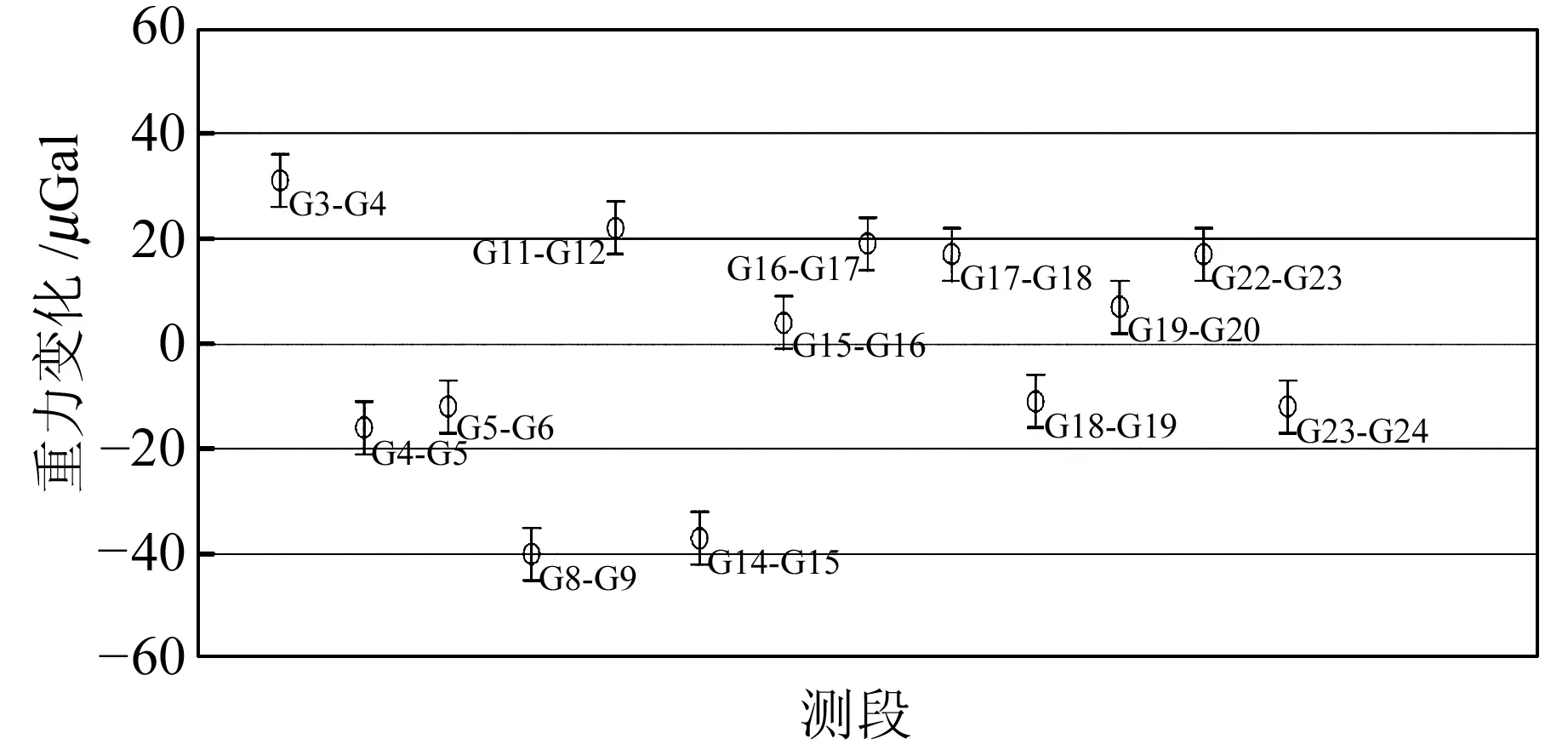
图2 庐山基线场相邻测站间重力段差观测结果的比较Fig.2 Comparison between observations of gravity differences at adjacent stations of Lushan gravimeter scale calibration field
3.2变化分析
地球系统质量分布的时空变化会产生时变重力场,能够反映各种地球动力学过程或地球物理事件,如构造运动、活动断裂孕震过程、地球自转变化、冰川均衡调整和气候变化过程伴随的地表质量变化等。在历次重力观测数据处理中,都考虑了重力固体潮、大气压力、海潮负荷和极移等改正,故基线场基点重力点值变化主要受构造运动、陆地水储量等因素影响。2005-11-26基线场周边发生5.7级地震,势必会对该地区造成一定程度的永久性重力变化。但由于无位错模型,本文无法给出其具体影响量级及大小[6]。构造运动包括同震引起的重力变化影响会对基线场产生同步效应,但地震对山体产生的影响,如塌方等会引起地物变迁并造成局部质量再分布,会影响基点间的重力段差。
为模拟该区域物质再分布引起的地表负荷重力效应,依据经典的表面负荷理论[7-8],重力负荷函数和负荷质量分布函数的全球卷积积分公式为:
(1)
式中,δg为负荷导致的地面测站(λ,θ)在t时刻的重力变化,S为整个地球表面,Gg(ψ)为重力负荷格林函数,P(λ′,θ′,t)为积分面元dS在t时刻的负荷压力,(λ′,θ′)为积分面元的经度和纬度。对陆地水储量而言,负荷压力P(λ′,θ′,t)为水密度与等效水高的乘积,即负荷面密度。
本文利用水文地球物理模型计算地表负荷重力变化。使用全球陆地数据同化系统(GLDAS)提供的Noah_0.25_M格网月数据(http://disc.sci.gsfc.nasa.gov/hydrology/data-holdings),其融合了来自地面和卫星的观察数据,提供最优化、近实时的地表状态变量[9]。将GLDAS提供的0.25°×0.25°格网点处的积雪数据以及1~4层的土壤水分数据综合起来得到该处总的水储存含量,然后扣除均值得到水储量的变化值。地球表面质量负荷引起的重力变化可以通过上述格林函数积分求得。
以基线场区域中心为计算点,计算自2009年以来的重力时间变化序列及年变率。由图3可以看出,陆地水储量引起的重力变化振幅为-5~5 μGal,年变率为-0.5 μGal/a。可见,与气候紧密相关的陆地水储量变化,对重力场的季节变化、年变化以及长期变化均有影响。地表垂直形变、基点附近山体和地物变迁等因素,也会对基线场基点重力值或相邻点重力差值造成影响。值得说明的是,庐山基线场由于庐山风景区道路改造过程中部分基点完全遭到破坏,其他保存完好的2000联测基点附近及周边地物变迁也较为严重,直接影响了基点附近的质量再分布以及局部环境。测段G8-G9和G14-G15的变化将近40 μGal,对于地质条件稳定的庐山基线场来讲,这是由2013年道路施工改造和建设引起的地物变迁造成的。因此,本次重新标定获得基线场初值是十分必要的。
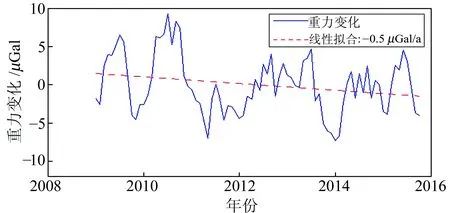
图3 陆地水储量引起的重力变化Fig.3 Gravity changes due to continental water storage
3.3效能评估
高精度基线场的建立,主要用于检测LCR、Burris和CG-5等类型相对重力仪的性能,包括一次项系数、动态零漂率和动态观测精度等技术指标的检验[10-11]。 其中一次项系数为短基线标定结果,庐山基线场的最大段差为200 mGal,无控制解算与控制解算结果差异约为60 μGal,如图4所示,则标定精度能够达到0.03%。若测区量程在该基线场覆盖范围,则可满足技术指标要求,否则还应进行重力长基线标定。
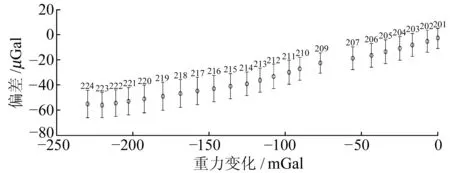
图4 无控制解算结果与控制解算结果的差值Fig.4 Gravity differences between the results by using datum controlled and without controlled
4 结 语
本文采用基于绝对重力控制的相对重力联测模式,建立了高精度的庐山短基线标定场。结果表明:1)4个基点的绝对重力测量结果精度优于±5.0 μGal;2)重力网平差后24个基点的重力点值精度均优于±5.0 μGal,平均精度为±3.0 μGal;3)各相邻测段段差精度均优于±3.0 μGal;4)2000联测与本次观测结果相比较(13个测段),绝对值最大变化为40.0 μGal,最小为4.0 μGal,平均为18.8 μGal,其中10个测段的变化值均在±20.0 μGal范围内。
庐山重力基线场初值测定结果表明,与以往的基线场测定方法相比,基于绝对重力控制的相对重力联测方法具有可行性强、精度高、测量方便和经济效益高的优点。
[1]刘冬至. 绝对与相对重力同步比测中的拉科斯特重力仪标定[J]. 地壳形变与地震, 1998, 18(1): 88-94(Liu Dongzhi. Calibration of LaCoste-Romberg Gravimeter in Absolute and Relative Gravimetric Conjunction[J]. Crustal Deformation and Earthquake, 1998, 18(1): 88-94)
[2]Torge W, Roder R H, Schnull M,等. 重力仪垂直标定基线(武汉)[J]. 地壳形变与地震, 1988, 8(2): 124-133(Torge W, Roder R H, Schnull M, et al. Gravimeter Calibration Line Wuhan, China[J]. Crustal Deformation and Earthquake, 1988, 8(2): 124-133)
[3]刘冬至, 王晓权, 邢灿飞, 等. 《2000国家重力基本网》短基线的检定与分析[J]. 大地测量与地球动力学, 2002, 22(4):
61-65(Liu Dongzhi, Wang Xiaoquan, Xing Canfei, et al. Verification and Analysis of Short Calibration Lines of 2000 National Gravity Network[J]. Journal of Geodesy and Geodynamics, 2002, 22(4): 61-65)
[4]Xing L L, Li H, Li J C, et al. Comparison of Absolute Gravity Measurements Obtained with FG5/232 and FG5/214 Instruments[J]. Geo-Spatial Information Science, 2009, 12(4):307-310
[5]邢乐林,申重阳,李辉,等. 欧洲绝对重力仪比对观测(ECGS’07)[J]. 地球物理学进展,2009,24(6):2 054-2 057(Xing Lelin, Shen Chongyang, Li Hui, et al. European Comparison of Absolute Gravimeters (ECGS’07)[J]. Progress in Geophysics, 2009, 24(6):2 054-2 057)
[6]Sun W K,Okubo S. Surface Potential and Gravity Changes Due to Internal Dislocations in a Spherical Earth- II. Application to a Finite Fault[J]. Geophys J Int, 1998, 132(1):79-88
[7]Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics and Space Physics, 1972,10(3):761-797
[8]Xu J Q, Sun H P. Deformation Response of a Snrei Earth to Surface Loads and Tidal Forces[J]. Chinese J Geophys,2003, 46(3): 465-477
[9]Rodell M,House P R,Jambor U,et al. The Global Land Data Assimilation System[J]. Bull Am Meteorol Soc,2004,85(3):381-394
[10]邢乐林,李辉,夏正超,等. CG-5 重力仪零漂特性研究[J].地震学报,2010,32(3):369-373(Xing Lelin, Li Hui, Xia Zhengchao, et al. Study on Zero Drift Characteristics of CG-5 Gravimeter[J]. Acta Seismologia Sinica,2010,32(3):369-373)
[11]梁伟锋,刘芳,祝意青,等. 重力仪一次项系数对重力场动态变化的影响研究[J]. 大地测量与地球动力学,2015,35(5):882-886(Liang Weifeng, Liu Fang, Zhu Yiqing, et al. Research on the Effect of One Degree Term of Chromatic Polynomial of Gravimeter on Gravity Dynamic Change[J]. Journal of Geodesy and Geodynamics, 2015,35(5):882-886)
Foundation support:Director Fund of Institute of Seismology, CEA, No. IS201326130; Special Fund for Earthquake Research of CEA,No.201508006, 201308004.
About the first author:XING Lelin, PhD,associate researcher, majors in gravity observation and data processing,E-mail:xinglelin@163.com.
Determination of Gravity Values for Lushan Short Gravity Calibration Baseline
XINGLelin1,2WANGLinhai1,2SUNShaoan1,2XUANSongbai1,2WANGJian1,2TANHongbo1,2
1Key Laboratory of Earthquake Geodesy, Institute of Seismology, CEA, 40 Hongshance Road, Wuhan 430071, China 2Wuhan Base of Institute of Crustal Dynamics,CEA, 40 Hongshance Road, Wuhan 430071, China
Using the FG5 absolute gravimeter, absolute gravity values are determined at three base gravity sites in Lushan and one datum site in Jiujiang seismic station to determine the Lushan calibration baseline.Further, twenty-five sites are determined using seven CG-5 relative gravimeters with two return measurements. The results show that the accuracy of gravity values at all of the base sites is better than ±5.0 μGal.The application of FG5 absolute gravimeter along with several relative gravimeters to construct short calibration baselines is a new and modern approach which has scientific significance as well as economic value.
baseline; calibration; absolute gravity measurements; relative gravity measurements
2016-03-26
邢乐林,博士,副研究员,主要从事重力观测及数据处理研究,E-mail:xinglelin@163.com。
10.14075/j.jgg.2016.09.001
1671-5942(2016)09-0753-04
P312
A
项目来源:中国地震局地震研究所所长基金(IS201326130);中国地震局地震行业科研专项(201508006,201308004)。

