海洋垂直重力梯度异常的计算及其在地形反演中的应用

欧阳明达 　孙中苗　翟振和　刘晓刚

1　地理信息工程国家重点实验室，西安市雁塔路中段1号，710054 2　西安测绘信息技术总站，西安市西影路36号，710054 3　西安测绘研究所，西安市雁塔路中段1号，710054



海洋垂直重力梯度异常的计算及其在地形反演中的应用

欧阳明达1,2孙中苗1,3翟振和1,3刘晓刚1,3

1地理信息工程国家重点实验室，西安市雁塔路中段1号，710054 2西安测绘信息技术总站，西安市西影路36号，710054 3西安测绘研究所，西安市雁塔路中段1号，710054

将测高重力异常、局部大地水准面和垂线偏差作为输入数据，计算海洋垂直重力梯度异常。以中西太平洋海域作为研究对象，对垂直重力梯度异常和海底地形的相关性进行分析，在20～200 km波段范围内利用梯度异常推估海底地形。结果表明，反演地形的相对精度在7.14%左右，在多海山地区精度较差。

垂直重力梯度异常；海底地形；导纳理论；重力异常

海底地形反演计算多基于空间重力场和深度数据在一定波段内高度相关的理论。Wang[1]提出可以采用垂直重力梯度异常进行海底地形反演，以得到独立于重力异常的海底地形模型。Wessel等[2]认为，垂直重力梯度异常能够放大短波信号，抑制长波信号，Moho面以下的密度差异和岩石圈有效弹性厚度等参数对海面垂直重力梯度异常的影响远小于对大地水准面和重力异常的影响。吴云孙等[3]将基于频域向下延拓的方法应用于垂直重力梯度异常反演南中国海海底地形模型的计算中，但结果并不理想。Kim等[4]在椭圆形海山模型假设的基础上，利用垂直重力梯度异常和非线性反演方法对全球的海山分布进行研究。胡敏章等[5]基于高斯海山模型，采用垂直重力梯度异常反演海底地形，并研究了地壳密度、岩石圈有效弹性厚度及截断波长对反演结果的影响，通过实测数据得到了高分辨率、高精度的海深模型。之后，胡敏章等[6]给出了垂直重力梯度异常和海底地形起伏之间的函数关系，并通过研究地壳均衡现象和高次项的影响量级发现，垂直重力梯度异常在中短波段(100～200 km)表现较优，并据此联合垂直重力梯度异常和船测海深数据，构建全球75°S～70°N的1′×1′海底地形模型。

本文利用卫星测高重力异常、大地水准面和垂线偏差计算垂直重力梯度异常，基于垂直重力梯度异常和海底地形的导纳关系，将中西太平洋海域作为研究对象，开展地形反演计算。考虑到垂直重力梯度异常具有放大短波信号的效果，引入低通/高通滤波器进行抑制。

1　基本原理

垂直重力梯度∂g/∂h分为正常和异常两个部分:

(1)

式中，γ为正常重力，Δg为重力异常。异常部分的计算有以下3种方法。

1)利用空间重力异常Δg表示：

(2)

式中，R为地球平均半径，θ′为计算点元P和流动点元的地心余纬，λ′为地心经度，Δg为P点的重力异常，l为计算点元P(R,θ,λ)到流动点元的距离。

2)利用局部大地水准面N表示：

(3)

式中，G为全球平均重力值，N为大地水准面起伏，φ为计算点的地心纬度(φ=π/2-θ)。该方程以大地水准面起伏N的一阶、二阶水平方向导数表示。

3)利用垂线偏差的子午分量ξ和卯酉分量η表示：

(4)

式中，|2GN/R2|≤0.05 E，可以忽略。

以115°～119°E、13°～17°N海域为例，利用已有模型计算垂直重力梯度异常，使用到的输入数据包括：1)重力异常，DTU10GRAV模型，1′分辨率；2)大地水准面，利用DTU10MSS(平均海水面)和DTU10MDT(瞬时海面地形)模型得到，1′分辨率。3)垂线偏差，IGG2006_DOV模型，2′分辨率。

式(2)中，被积函数随距离的增加而迅速减少，只需将积分扩展到计算点的邻近即可[7]，令重力异常积分半径为500 km；式(3)中，令计算点周围10′×10′的大地水准面数据作为起算；式(4)中，令计算点周围5′×5′的垂线偏差作为起算。图1给出了利用重力异常计算的垂直重力梯度异常模型，其反映了中高频的海底地形信息，突出的海山、宽阔的海底平原等反映出了明显的地形特征。

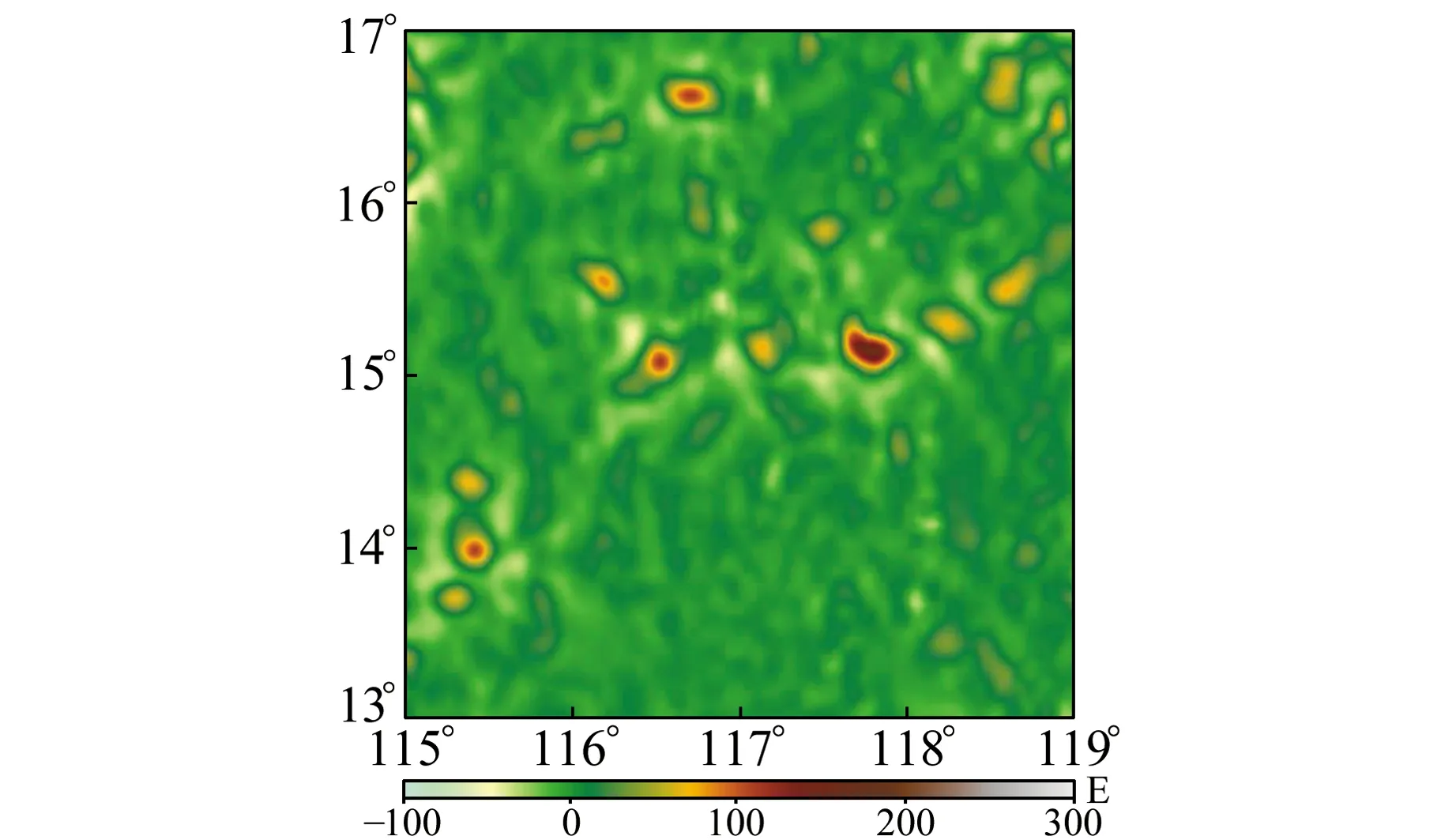
图1　SIO垂直重力梯度异常模型Fig.1　The gravity gradient anomalies model published by SIO

将本文反演模型与斯克里普斯海洋研究所(SIO)发布的垂直重力梯度异常进行比较。将采用式(2)～(4)计算的梯度异常模型分别定义为模型1、模型2和模型3。表1给出了垂直重力梯度异常模型与SIO发布的异常模型的差异。大地水准面反映的是重力场长波特性(更平滑)，垂线偏差反映的波长也大于空间重力异常，表1中结果的不同精度对应不同重力场数据反映的梯度异常波长段信息，波长越长，精度越差，对梯度异常模型的贡献就越小；波长越短，垂直重力梯度异常模型越精细，精度越高，对梯度异常模型的贡献越大。模型比较结果的中误差在±11.747 E内，采用大地水准面数据得到的异常模型精度较低，采用重力异常数据得到的异常模型精度较高，且仅耗时4 min左右。

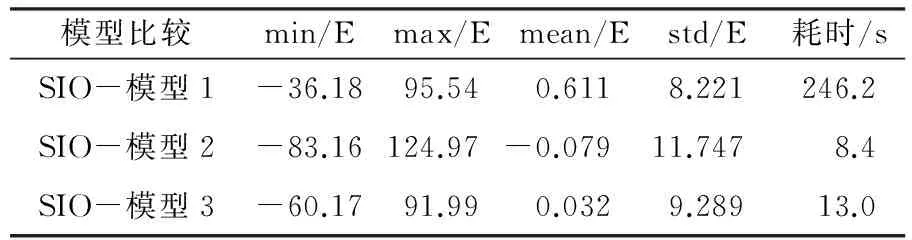
表1　垂直重力梯度异常与SIO模型的差异

2　海底地形/梯度异常导纳及相关性分析

胡敏章等[6]给出了频率域内垂直重力梯度异常和海底地形之间的响应函数关系式：

(5)

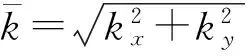
(6)

式中，g为平均重力加速度，D为岩石圈的挠曲刚度，其与岩石圈的有效弹性厚度Te有关：

(7)

式中，υ为岩石圈的泊松比，E为弹性模量。

r的最小二乘解可以写为：

(8)

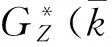
图2为垂直重力梯度异常和海底地形的相关关系图。可以看出，在波长段30～500 km，两者的相关关系大于0.5(本文反演波长段在20～200 km)。顾及地壳均衡导纳的影响会增加计算量，但不会提高计算精度[6]，因此，本文在构建海底地形模型时，不考虑地壳均衡的影响。

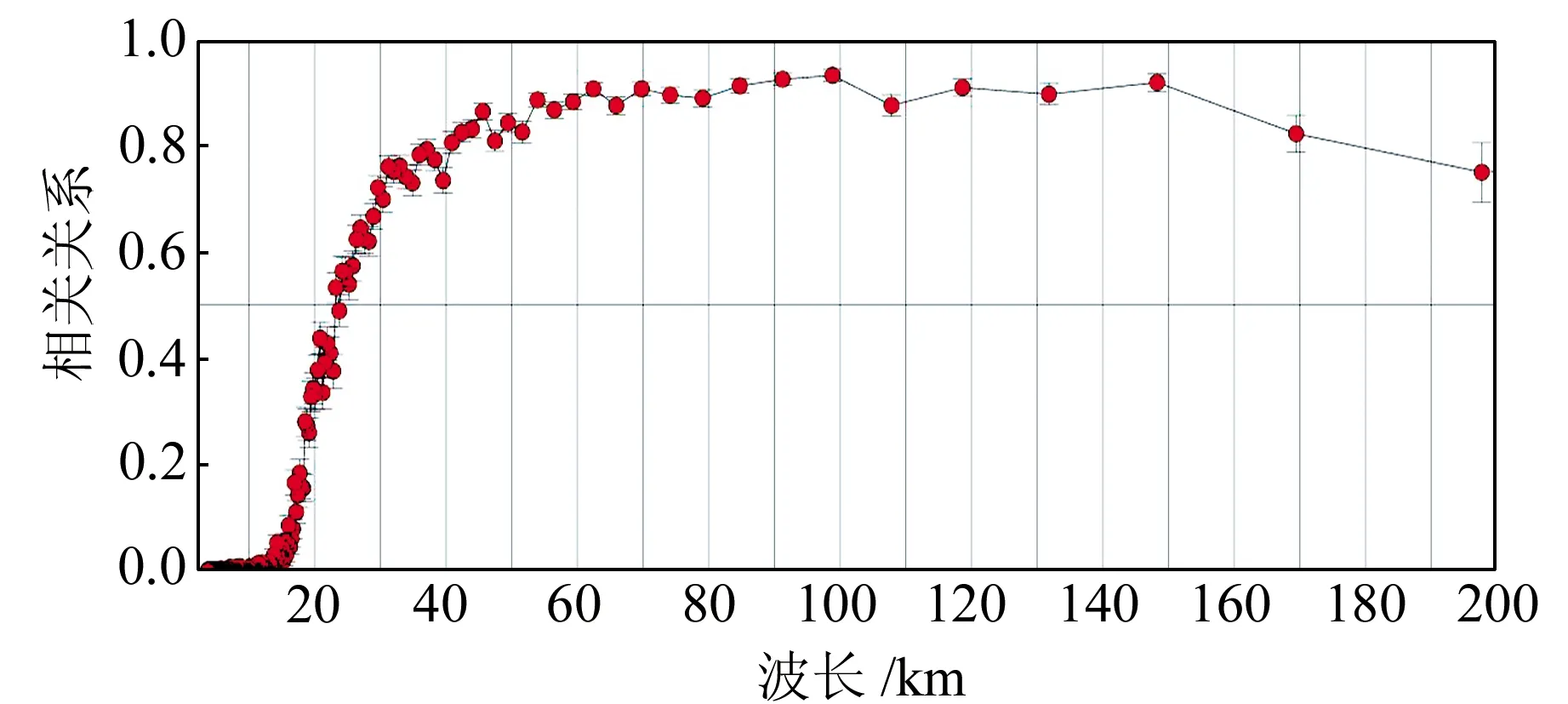
图2　垂直重力梯度异常与海底地形的关系Fig.2　The correlation between the bathymetry and gravity gradient anomalies

3　结果及讨论

3.1计算过程

以中西太平洋海域为研究对象，其上分布有众多的海山、海丘，经纬度范围为150°～170°E、10°～18°N。海域内的船测水深分布见图3，垂直重力梯度异常见图4。梯度异常模型由测高重力异常算得，由于部分点位的船测水深存在粗差，因而必须先进行粗差剔除。将剔除粗差后剩余船测点的2/3作为水深控制点，1/3作为检核点，控制点和检核点不重复，且在海域内均匀分布。垂直重力梯度异常衰减过快，在20～200 km波段内对地形信息敏感。图5为垂直重力梯度异常法的计算流程，构建步骤如下。

图3　船测航迹Fig.3　Distribution of shipborne tracks

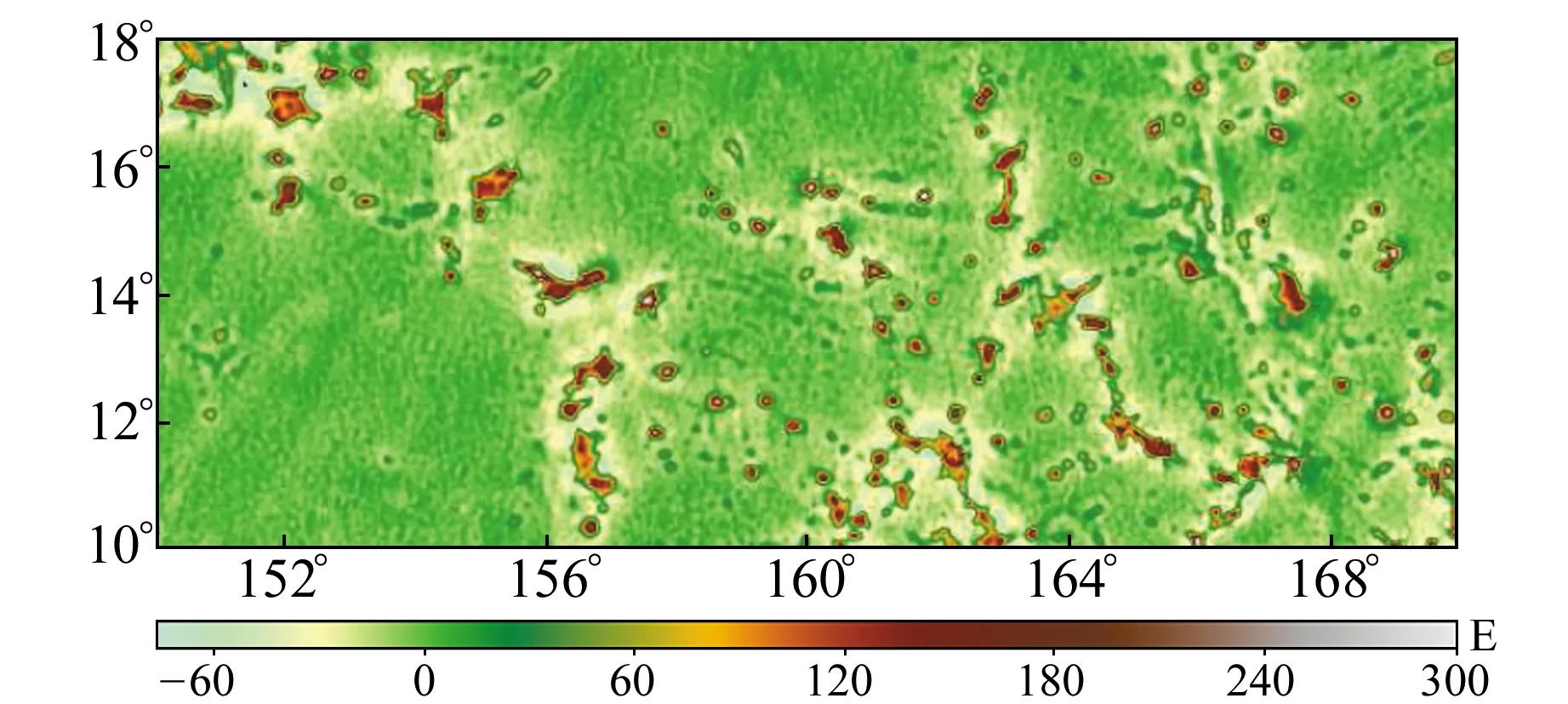
图4　垂直重力梯度异常Fig.4　The vertical gravity gradient anomalies

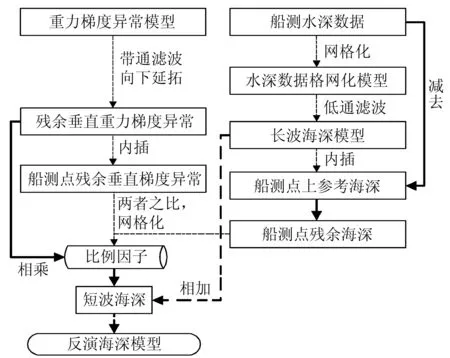
图5　垂直重力梯度异常法计算流程图Fig.5　The bathymetry predicting procedure

1)将船测水深数据格网化，采用低通滤波得到大于200 km波长的长波海底地形。重力异常经20～200 km的带通滤波、向下延拓等处理后，获得反演波段内的垂直重力梯度异常。

2)比例因子通过离散船测点确定。在船测点上对长波海底地形内插计算后，从实测水深值中减去此长波值，得到船测点上的残余海深。在船测点上对反演波段内的垂直重力梯度异常模型内插计算，得到离散的残余梯度异常值。离散的残余海深和残余梯度异常值之比即为比例因子，剔除其中的粗差，并将其格网化，即可得到比例因子格网(图6)。比例因子格网的确定是该方法的关键，其受离散船测点数量和分布等的影响较大。

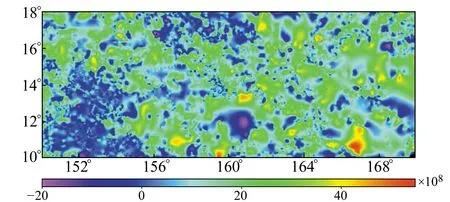
图6　比例因子Fig.6　The proportion factors

3)比例因子格网与反演波段内的垂直重力梯度异常之积即为残余的海深格网，将长波海底地形和残余海深格网叠加得到海底地形(图7)。

图7　海底地形模型Fig.7　The bathymetry model

3.2精度评定

表2给出了本文反演模型与ETOPO1、GEBCO、SIO和GINA模型的精度统计结果。可以看出，采用垂直重力梯度方法得到的反演模型精度略低。表3给出了反演模型在不同水深层的精度反演结果。可以看出，随着水深层的向上变化，模型精度不断降低。将检核点上的精度比较结果与实际水深之比定义为相对精度，图8给出了点位上相对精度的绝对值大小。可以看出，在多海山和海礁的地区，相对精度较差。

3.3粗差分析

将相对精度大于40%的点定为粗差。图9给出了粗差点的位置分布，共计659个，约占总数的1.42%。可以看出，粗差点主要集中在右侧海域，该部分海域地形起伏变化剧烈，对反演模型精度造成了很大影响。

图8　检核点相对精度的绝对值统计Fig.8　Statistic of absolute values of relative precision of check points

模型min/mmax/mmean/mstd/mRMS/mETOPO1-3754.375744.6024.13352.126.87%SIO-3745.465580.402.59257.255.02%GEBCO-3744.685647.146.24267.475.22%GINA-3737.35620.73-14.83300.145.86%本文模型-3413.064881.82142.46365.707.14%

表3　检核点精度的水深分层统计及比较

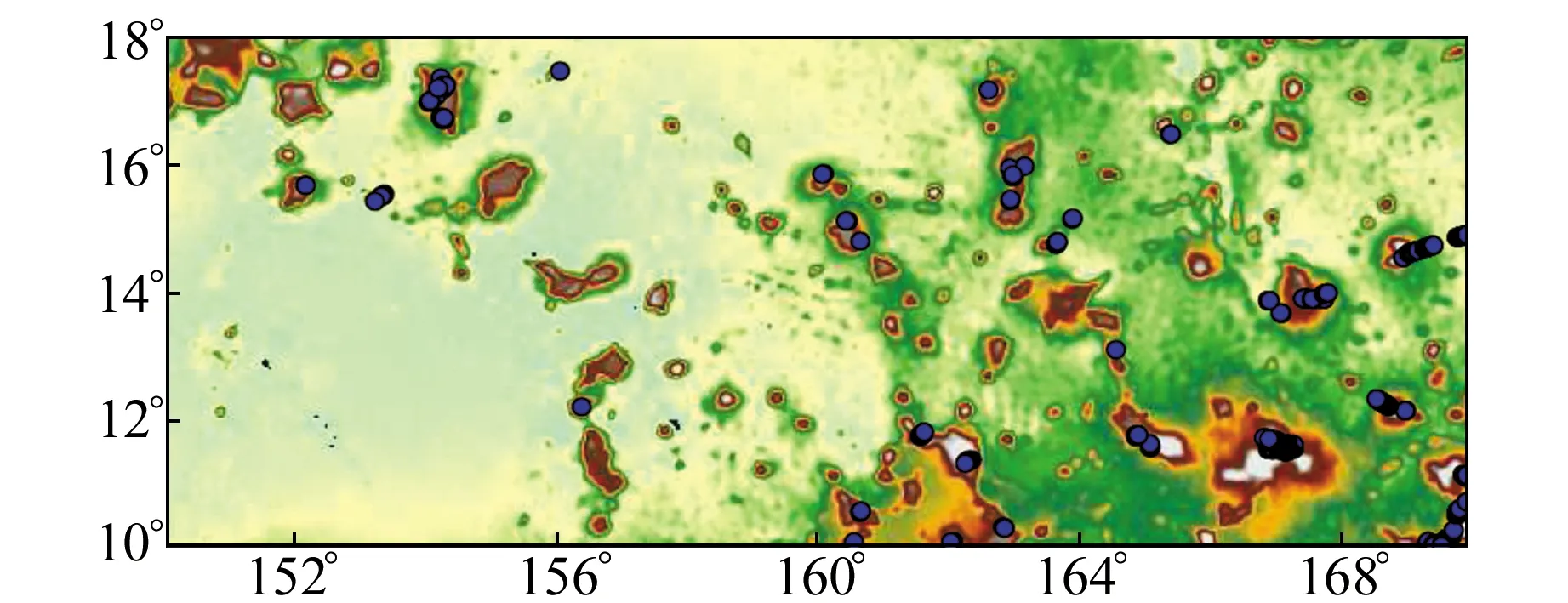
图9　检核点粗差分布Fig.9　The distribution of grass error points

4　结　语

1)将测高重力异常、局部大地水准面和垂线偏差作为输入数据可以得到垂直重力梯度异常，采用重力异常得到的梯度异常模型精度较高。

2)梯度异常反演海底地形的关键在于比例因子的确定，计算比例因子需要足够数量和分布状况良好的船测点作为控制，从而使残余海底地形和波段内梯度异常保持良好的线性关系。

3)采用梯度异常反演海底地形模型结果可靠，方法简便，不涉及复杂地球物理参数的求取，其相对精度为7.14%左右，略低于国际上现有的公开发布的地形模型。其中，浅海海域地形精度低于深海海域，多海山、海礁、海沟等地形的海域精度低于地形平坦的海域。

[1]Wang Y M. Predicting Bathymetry from the Earth Gravity Gradient Anomalies[J].Marine Geodesy, 2000, 23(4):251-258

[2]Wessel P,Lyons S.Distribution of Large Pacific Seamounts from Geosat/ERS-1:Implication for the History of Intraplate Volcanism[J]. Journal of Geophysical Research:Solid Earth, 1997,102(B10): 22 459-2 2475

[3]吴云孙,晁定波,李建成，等. 利用测高重力梯度异常反演中国南海海底地形[J].武汉大学学报：信息科学版,2009,34(12):1 423-1 425(Wu Yunsun, Chao Dingbo, Li Jiancheng, et al. Recovery of Ocean Depth Model of South China Sea from Altimetric Gravity Gradient Anomalies[J]. Geomatics and Information Science of Wuhan University, 2009,34(12):1 423-1 425)

[4]Kim S S,Wessel P. New Global Seamount Cencus from Altimetry Derived Gravity Data[J].Geophysical Journal International,2011,186(2):615-631

[5]胡敏章,李建成,李大炜.利用垂直重力梯度异常反演海底地形[J].大地测量与地球动力学,2012,32(5):95-98(Hu Minzhang, Li Jiancheng, Li Dawei. Bathymetry Prediction from Vertical Gravity Gradient Anomalies[J]. Journal of Geodesy and Geodynamics, 2012,32(5):95-98)

[6]胡敏章,李建成,邢乐林.由垂直重力梯度异常反演全球海底地形模型[J].测绘学报,2014,43(6):558-565(Hu Minzhang, Li Jiancheng, Xing Lelin. Global Bathymetry Model Predicted from Vertical Gravity Gradient Anomalies[J]. Acta Geodaetica et Cartographica Sinica,2014,43(6):558-565)

[7]Heiskanen W A, Moritz H. Physical Geodesy[J]. Bulletin Géodésique, 1967, 86(1): 491-492

Foundation support:National Natural Science Foundation of China,No,41304022; Open Fund of State Key Laboratory of Geo-Information Engineering, No.SKLGIE2015-M-1-2.

About the first author:OUYANG Mingda, assistant engineer, majors in geodetic data processing, E-mail: oymd6666@163.com.

The Calculation of Vertical Gravity Gradient Anomalies and Its Application in Bathymetry Inversion

OUYANGMingda1,2SUNZhongmiao1,3ZHAIZhenhe1,3LIUXiaogang1,3

1Stake Key Laboratory of Geo-Information Engineering,1 Mid-Yanta Road, Xi’an 710054,China 2Xi’an Division of Surveying and Mapping,36 Xiying Road, Xi’an 710054,China 3Xi’an Research Institute of Surveying and Mapping,1 Mid-Yanta Road, Xi’an 710054,China

Altimeter gravity anomalies, geoid and vertical deflection are used to calculate oceanic vertical gravity gradient anomalies. The correlation between the gravity gradient anomalies and bathymetry is analyzed. Taking islands in Midwest Pacific Ocean as examples, the bathymetry model is inversed in 20～200 km wavelength; results show that the relative precision of the bathymetry model is 7.14%. In seamount distributed areas, the relative precision is lower.

vertical gravity gradient anomalies; bathymetry; admittance theory; gravity anomalies

2015-09-21

欧阳明达，助理工程师，主要研究方向为大地测量数据处理，E-mail：oymd6666@163.com。

10.14075/j.jgg.2016.09.004

1671-5942(2016)09-0766-04

P223

A

项目来源：国家自然科学基金(41304022)；地理信息工程国家重点实验室开放基金(SKLGIE2015-M-1-2)。