一种顾及GNSS系统间偏差的伪距单点定位方法

徐龙威　刘　晖　刘玉洁　舒　宝　张　明　钱　闯

1　武汉大学卫星导航定位技术研究中心，武汉市珞喻路129号，430079 2　河南省遥感测绘院，郑州市黄河路8号，450003



一种顾及GNSS系统间偏差的伪距单点定位方法

徐龙威1刘晖1刘玉洁2舒宝1张明1钱闯1

1武汉大学卫星导航定位技术研究中心，武汉市珞喻路129号，430079 2河南省遥感测绘院，郑州市黄河路8号，450003

对系统间偏差的成分和影响因素进行分析，发现各项改正后残余误差对系统间偏差估值的影响可归结为与卫星编号和广播星历更新相关。提出一种新的顾及参与解算卫星构成的系统间偏差估计方案，新方案能够在仅有4颗多模GNSS卫星可见时提供可靠的位置服务。

多模GNSS；系统间偏差；卫星编号；定位

对于常规导航用户，观测条件较差导致大量观测误差被系统间偏差(inter system bias, ISB)吸收[1-2]，ISB的稳定性变弱。Montenbruck等[3]在分析CONGO网络测站性能时，首次提出GPS/Galileo测距码ISB，并从理论上证明ISB与接收机和测距码的类型有关。Torre等[2]利用实测数据分别基于精密轨道和广播星历分析ISB的变化规律，证明了ISB与接收机类型相关的特性。文献[4-5]利用ISB短时间内变化不大的特性，将在可见卫星充足历元求得的ISB作为已知参数，引入可见卫星不足历元进行系统间的偏差补偿，减少观测模型中未知参数的个数，在损失一定精度的条件下实现了GPS/GLONASS双系统仅4颗星的定位解算。由于不同卫星观测误差的差异明显且会被ISB吸收，所以不同卫星参与解算会得到不同的ISB估值。因此，在进行系统间偏差补偿时，顾及当前历元可见卫星的观测误差，能够减少Cai等[4]提到的精度损失。

1　系统间偏差构成和影响因素

多模GNSS时空基准和信号硬件延迟等因素的差异都会导致系统间偏差，可利用伪距观测方程对系统间偏差的构成和影响因素进行推导:

(1)

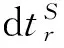
时空转换后，常规伪距单点定位误差模型为：

V=HX+L

(2)

式中，δx、δy、δz为接收机真实坐标与近似坐标之差，dtsys_GR、dtsys_GC、dtsys_GE为以GPS为基准与其他GNSS系统的接收机钟差参数之差，即系统间码偏差。此时多种观测误差会导致ISB的估值包含时间系统间偏差、轨道误差、卫星钟差、对流层延迟、多路径、接收机硬件延迟以及观测噪声之差等。Montenbruck等[6]对GNSS广播星历偏差进行分析，广播星历SSIRE在m级，同一时刻不同卫星广播星历偏差不同，且GLONASS卫星广播星历误差受星历更新影响具有明显周期性。大气延迟和多路径效应主要与卫星信号传播路径相关，可以理解为与卫星编号相关。另外，GLONASS卫星频率不同，导致不同卫星的信号接收机硬件码延迟不同[7]，也可被当作与卫星编号相关。卫星观测值的各项观测误差都会影响系统间偏差估计，这些误差都可以视为与卫星编号相关且短时间内变化不大。因此，在估计ISB时顾及卫星编号能够明显提高估值对当前历元的适应性。

ISB的分析基于伪距单点定位数学模型，对流层延迟采用Saastamoinen模型改正，电离层采用消电离层组合(GPSL1/L2，GLONASSL1/L2，BDSB1/B2，GalileoE1/E5a)，实验分析均基于GPST。下文中，G代表GPS，R代表GLONASS，C代表BDS，E代表Galileo。

2　系统间偏差特性分析

2.1GPS作为参考系统合理性分析

本文以GPS为基准系统。不同的GPS卫星参与解算会对ISB估值造成影响，因此，本文利用不同数目的GPS卫星参与解算，分析其对ISB估计的影响。如图1所示(以G-RISB为例)，不同数目的GPS卫星参与解算，ISB估值差异在5ns以内。随着参与解算的GPS卫星数目的减少，观测模型的稳健性减弱，ISB稳定性也随之变差。参与解算的GPS卫星为随机选取，其他系统可见卫星全部参与解算。总之，不同颗数的GPS卫星参与解算对ISB估值的影响远小于ISB估值的量级。

图1　GPS卫星对ISB的影响Fig.1　The influence of GPS satellite to inter system bias

2.2系统间偏差特性分析

选取6个不同类型接收机的MEGX跟踪站(表1)2013-11-25的观测数据，截止高度角设置为10°，采样间隔30s。

从图2～4可以看出，ISB与接收机类型相关。对于GLONASS(图2)，ISB比较稳定，24h变化区间在15ns以内，与时间相关性很强，相邻两个历元差异很小。但ISB经常出现跳跃，且发生时刻均为GLONASS广播星历更新时刻，可知广播星历更新是ISB的重要影响因素。

表1　MEGX站接收机类型以及兼容系统

图2　不同类型接收机获得观测值的G-R ISB估值Fig.2　G-R ISB estimates for different types of receiver observations

从图3看出，所有测站的ISB估值相邻历元间差异很小，CUT0和MAL2的ISB稳定性较强。这两个站ISB稳定性好的主要原因是其可见BDS卫星大于6颗，ISB估值为多颗卫星观测值的加权平均，卫星数越多稳定性越好。BRUX仅能观测到3颗左右BDS卫星，导致其ISB稳定性较差。

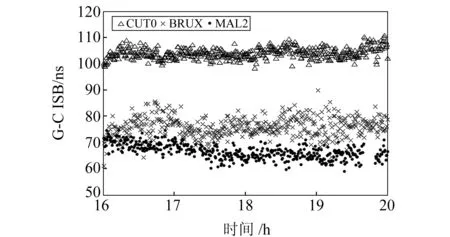
图3　不同类型接收机获得观测值的 G-C ISB估值Fig.3　G-C ISB estimates for different types of receiver observations

如图4，目前Galileo在轨卫星较少，导致G-E ISB稳定性略差，不同接收机间的ISB差异也十分明显。

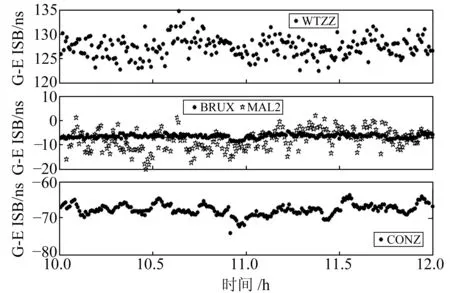
图4　不同类型接收机获得观测值的G-E ISB估值Fig.4　G-E ISB estimates for different types of receiver

2.3单颗卫星对ISB影响分析

对单颗卫星ISB的分析见图5～7。单颗卫星的ISB估计方法与系统间ISB估计方法类似。以1颗GLONASS卫星的ISB为例，所有GPS卫星+1颗GLONASS卫星解算获得该颗GLONASS卫星的ISB。

由图5可知，GLONASS卫星ISB变化与时间相关，具有明显的周期性，且与广播星历更新时间相符。与下文其他GNSS系统相比，不同卫星对应的ISB差异更明显，R14与R08对应的ISB相差20 ns左右。这主要是由于GLONASS采用频分多址技术，不同的卫星信号频率不同，导致接收机硬件延迟差异。

图5　不同GLONASS卫星G-R ISB(GOP6站)Fig.5　G-R ISB for different GLONASS satellites(GOP6 station)

图6为不同BDS卫星ISB变化规律，较差稳定且无明显周期性，但与时间的相关性明显，星历历元估值差异在3 ns以内。当卫星高度角较低时，ISB与卫星高度角的相关性非常明显，这主要是由于BDS码偏差的作用。

图6　不同BDS卫星G-C ISB (CUT0站)Fig.6　G-C ISB for different BDS satellites(CUT0 station)

如图7所示，不同的Galileo卫星ISB相差不大，单颗卫星ISB在固定区间内随机分布，稳定性优于GLONASS和BDS，变化范围一般在10 ns以内。观测时段GPST 00:00～02:00之间，ISB出现剧烈跳动是由E20卫星观测噪声造成。单颗Galileo卫星ISB未出现类似GLONASS的周期性波动，也未出现类似BDS的与高度角相关变化。但目前Galileo卫星过少，广播星历播发稳定性不足，许多时段的广播星历卫星信号群延差改正参数(BGD)均不可用。

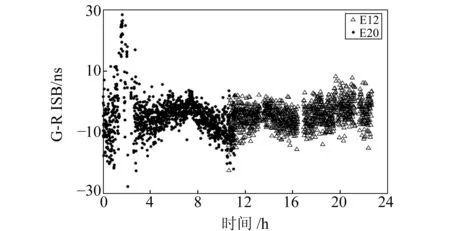
图7　不同Galileo卫星G-E ISB(MAL2站)Fig.7　G-E ISB for different Galileo satellites (MAL2 station)

3　ISB在定位中的应用

3.1可见卫星不足条件下多模组合单点定位

多模组合单点定位通常采用增加钟差参数的方法处理，最少需要3+n颗(n为参与解算的GNSS系统种类)可见卫星才能实现定位解算。实时低精度导航用户的定位环境比较复杂，经常出现卫星信号被遮挡，导致只有少数卫星可见。此时，通常利用ISB短时间内的稳定性，将基于观测值充足历元求取的ISB作为先验值，引入观测模型以减少未知参数个数，实现卫星数不足条件下的单点定位。然而不同的卫星参与解算会得到不同的ISB估值，此时的ISB先验值不适用于当前历元。基于本文提出的ISB估计方法，利用一个存储下来的历史历元观测值，分别求取当前观测值不足历元可见卫星与GPS系统间的ISB，并用于当前历元定位。

3.2实验分析

利用6个MGEX跟踪站(表1)2013-11-25的观测数据，设计3种实验方案，并根据方案要求随机选取相应颗数的卫星观测值。

方案1：随机选取4颗GPS卫星进行单点定位；方案2：随机选取来自多系统的4颗卫星，引入不考虑卫星号的ISB进行定位；方案3：随机选取来自多系统的4颗卫星，引入顾及卫星号的ISB进行定位。

方案1中，随机选取参与解算的GPS卫星。方案2和方案3中，CUT0、MAL2和BRUX站为在当前历元可见卫星中随机选取1颗GPS、1颗GLONASS、1颗BDS和1颗Galileo卫星。GOP6、CONZ和WTZZ站不能接收到BDS测距信号，于是随机选取2颗GPS、1颗GLONASS和1颗Galileo卫星。设置存储历元每5 min更新一次，截止高度角10°，历元间隔30 s， PDOP阈值40。方案2根据历史历元中所有观测值求取的ISB进行改正。方案3为求取当前历元可见卫星对应的ISB，并改正当前历元相应的观测值，在求取ISB时，历史历元中所有GPS观测值均参与解算。

表2为上述3种方案24 h定位结果。可以看出，方案3定位精度最高。

表2　定位偏差RMS统计

4　结　语

影响ISB的各项误差源均可看作与卫星编号相关，因此提出一种基于卫星编号的ISB估计方案。以GPS为参考系统，利用不同类型接收机的观测数据估计ISB，发现不同卫星参与解算ISB估值存在明显差异。最后，将顾及卫星号和广播星历更新的ISB估计方案应用于可见卫星不足时的伪距单点定位，其精度明显改善，且适用于多种类型接收机。

[1]徐龙威，刘晖，张明，等.不同截止高度角多模GNSS组合单点定位性能分析[J]. 大地测量与地球动力学,2015,35(6)：987-991(Xu Longwei, Liu Hui, Zhang Ming, et al. Performance Assessment of Multi-GNSS Single Point Positioning with Different Cut-off Elevation Angles[J]. Journal of Geodesy and Geodynamics,2015, 35(6):987-991)

[2]Torre A D, Caporali A. An Analysis of Intersystem Biases for Multi-GNSS Positioning[J]. GPS Solutions, 2015, 19(2): 297-307

[3]Montenbruck O, Hauschild A, Hessels U. Characterization of GPS/GIOVE Sensor Stations in the CONGO Network[J]. GPS Solutions, 2011, 15(3): 193-205

[4]Cai C S, Yang G. A Combined GPS/GLONASS Navigation Algorithm for Use with Limited Satellite Visibility [J].Journal of Navigation, 2009, 62(4): 671-685

[5]Angrisano A, Gaglione S, Gioia C. Performance Assessment of GPS/GLONASS Single Point Positioning in an Urban Environment[J]. Acta Geodaetica et Geophysica, 2013, 48(2): 149-161

[6]Montenbruck O, Steigenberger P, Hauschild A. Broadcast Versus Precise Ephemerides: A Multi-GNSS Perspective[J]. GPS Solutions, 2015, 19(2):321-333

[7]张雪. GNSS系统时间偏差监测精度改善及评估[D].西安：中国科学院国家授时中心,2014(Zhang Xue. Research on the Accuracy Improvement and Assessment of GNSS System Time Offset Monitoring[D]. Xi’an：National Time Service Center, CAS, 2014)

Foundation support:National Key Research and Development Program of China, No.2016YFB0800405

About the first author:XU Longwei, PhD candidate, majors in multi-GNSS navigation and positioning, E-mail：xlw_ltu2012@163.com.

A Multi-GNSS Pseudorange Positioning Method with Inter System Bias

XULongwei1LIUHui1LIUYujie2SHUBao1ZHANGMing1QIANChuang1

1GNSS Research Center, Wuhan University, 129 Luoyu Road, Wuhan 430079, China 2Institute of Remote Sensing and Surveying and Mapping of Henan Province, 8 Huanghe Road, Zhengzhou 450003, China

In this paper, with the derivation of code observation equation, the structure and influence factors of inter system bias are analyzed. We discover that all factors for low precision navigation can be treated as related to satellite number. A new inter system bias parameter estimation solution is proposed. Finally, the new solution is applied to multi-GNSS positioning, providing reliable positioning information for real-time low precision users when only 4 multi-GNSS satellites are visible.

multi-GNSS; inter system bias; satellite number; positioning

2015-09-18

徐龙威，博士生，主要研究方向为多模GNSS导航定位，E-mail： xlw_ltu2012@163.com。

10.14075/j.jgg.2016.09.013

1671-5942(2016)09-0813-04

P228

A

项目来源：国家重点研发计划(2016YFB0800405)。