高考数学的四种审题方法

于真灵

高考数学的四种审题方法

于真灵

波利亚解题的四个步骤：弄清问题、拟定计划、实现计划、代入回顾。其中的弄清问题即审题。审题是解题的基础和关键，一切解题的思路、方法、技巧都来源于认真审题。本文给出高考数学的四种审题方法，供老师们复习参考。

方法一：审视隐含，想周全

审题指导

又f（log2a）=f（|log2a|），且f（x）在［0，+∞）上单调递增，所以|log2a|≤1⇒-1≤log2a≤1，解得2，故选C。

点评有的数学题条件并不明显，而是寓于概念、存于性质或含于图中，审题时，就要注意深入挖掘这些隐含条件和信息，从而在解题时避免因忽视隐含条件而出现错误。

方法二：审视结构，定方案

例2△ABC中角A，B，C的对应边分别为a，b， c，满足，则角A的取值范围是（ ）。

审题指导

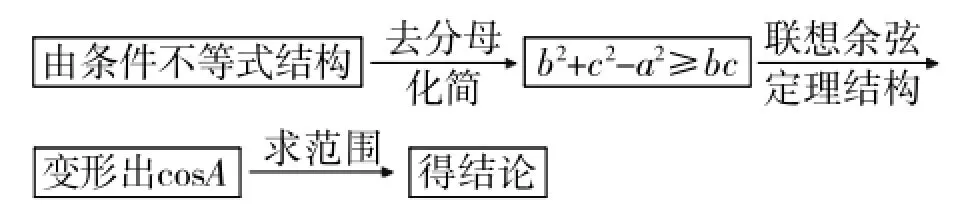
点评数学问题中的条件和结论很多都是以数式的结构形式进行搭配和呈现的。在这些问题的数式结构中，往往都隐含着某种特殊关系。认真审视数式的结构特征，对数式结构进行深入分析，加工转化，可以寻找到突破问题的方案。

方法三：审视图形，抓特点

例3（2015·北京理5）某三棱锥的三视图如图所示，则该三棱锥的表面积是（ ）。

审题指导

简解作出三棱锥的示意图如图，在△ABC中，作AB边上的高CD，连接SD。在三棱锥S-ABC中，SC⊥底面ABC，SC=1，底面三角形ABC是等腰三角形，AC=BC，AB边上的高CD=2，AD=BD=1，斜高。

所以S表=S△ABC+S△SAC+S△SBC+S△SAB=×2×2+×1××1××2×= 2+，故选C。

点评在一些高考数学试题中，问题的条件往往是以图形的形式给出，或将条件隐含在图形之中，因此在审题时，要善于观察图形，洞悉图形所隐含的特殊的关系、数值的特点、变化的趋势，抓住图形的特征，利用图形所提供的信息解决问题。

方法四：审视图表（数据），找关联

例4（2015·全国卷Ⅱ17）某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了20个用户，得到用户对产品的满意度评分如下：

A地区：6273819295857464 537678869566977888827689

B地区：7383625191465373 648293486581745654766579

（1）根据两组数据完成两地区用户满意度评分的茎叶图，并通过茎叶图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）；

（2）根据用户满意度评分，将用户的满意度从低到高分为三个等级：

满意度评分　低于70分　70分到89分　不低于90分满意度等级　不满意　满意　非常满意

记事件C：“A地区用户的满意度等级高于B地区用户的满意度等级”，假设两地区用户的评价结果相互独立。根据所给数据，以事件发生的频率作为相应事件发生的概率，求C的概率。

审题指导

简解

通过茎叶图可以看出，A地区用户满意度评分的平均值高于B地区用户满意度评分的平均值；A地区用户满意度评分比较集中，B地区用户满意度评分比较分散。

（2）记CA1表示事件：“A地区用户的满意度等级为满意或非常满意”；

CA2表示事件：“A地区用户的满意度等级为非常满意”；

CB1表示事件：“B地区用户的满意度等级为不满意”；

CB2表示事件：“B地区用户的满意度等级为满意”，

则CA1与CB1独立，CA2与CB2独立，CB1与CB2互斥，C=CB1CA1∪CB2CA2。

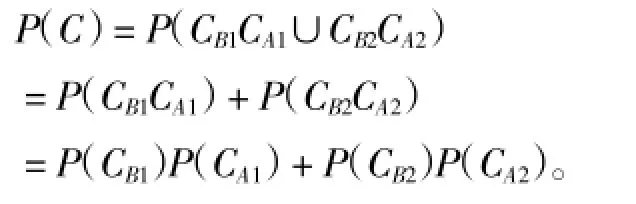
由所给数据得CA1，CA2，CB1，CB2发生的频率分别为，故，，。

点评题目中的图表、数据包含着问题的基本信息，也往往暗示着解决问题的目标和方向。在审题时，要认真观察分析图表、数据的特征和规律，找到其中的内在联系，为解决问题提供有效的途径。

（作者单位：绥宁县第一中学）