基于混合蛙跳算法的软硬件划分方法*

卢　晨，毛乐乐，黄　勇

(广西民族大学，a.信息科学与工程学院;b.网络与信息化管理中心，广西 南宁　530006)



基于混合蛙跳算法的软硬件划分方法*

卢晨a，毛乐乐a，黄勇b

(广西民族大学，a.信息科学与工程学院;b.网络与信息化管理中心，广西 南宁530006)

软硬件划分问题是嵌入式系统软硬件协同设计的关键问题，划分结果的好坏直接影响着系统性能的优劣.将软硬件划分问题转化成0-1背包问题，提出了一种基于混合蛙跳算法求解软硬件划分问题的方法.该方法在求解软硬件划分问题的过程中，不断地寻找更优可行解，逐渐达到搜索全局最优解，使得系统的软硬件实现总代价最小.实验结果表明，该方法能很好求解软硬件划分问题，所应用算法的收敛速度明显优于对比算法.

软硬件协同设计；软硬件划分；混合蛙跳算法；启发式算法

0　引言

嵌入式系统设计中，系统组件功能可由软件或硬件实现，软件实现具有成本低、配置灵活的优点，但执行速度慢；硬件实现执行效率高，功耗小，但成本高[1].早期的嵌入式系统规模小，功能简单，设计人员凭借经验实现软硬件划分在一定程度上可以满足设计需求.随着嵌入式系统应用需求的日益增长，系统较之前更为庞大复杂，设计周期也越来越短，科学合理的软硬件划分方法显得尤为重要.因此，软硬件划分成为嵌入式系统软硬协同设计中的首要问题，其主要目标是如何兼顾系统的性能和成本，达到两者的最佳结合.

近年来，国内外已经对关于软硬件划分的问题进行了大量的研究，软硬件问题已经被证明为NP问题[1-3]，已有的解决方法主要有两类算法：精确算法和启发式算法.精确算法有整数线性规划、动态规划算法等规划类方法，这类算法没有明确的目标函数，约束条件多，计算时间复杂度较高，计算时间会很长，一般用于较小规模的划分问题，当问题规模较大时，并不适用.启发式算法可广泛应用于求解规模较大的划分问题，例如遗传算法(GA)[4]，量子遗传算法(QGA)[5]，混合量子遗传算法(HQGA)[6]，粒子群优化算法(PSO)[7-8]等智能优化算法.其中，混合蛙跳算法[9-10]是一种新兴的基于群智能的亚启发式智能优化算法, 该算法具有概念简单，参数少，计算速度快，全局搜索寻优能力强，易于实现的特点.目前，尚未看到利用混合蛙跳算法求解软硬件划分问题的研究工作.

为便于求解软硬件划分问题，首先将划分问题转换成标准0-1背包问题，然后利用混合蛙跳算法求解0-1背包问题，从而实现对软硬件划分问题的求解，最后通过实验证明该方法的有效性和可行性.

1　软硬件划分问题的数学模型

1.1软硬件划分问题

求解软硬件划分问题时，通常使用无向图来描述任务流图.

定义1R={R1，R2，…，Rn}代表划分系统的所有任务节点集合,其中Ri表示第i个任务节点，其中i=1,2,…,n.图中的一个节点就是对应划分系统的一个任务，每个节点包含其软件、硬件代价信息.

定义2系统总代价由软件代价和硬件代价组成，即系统总代价为软件代价与硬件代价之和.

定义3软硬件划分问题中x=(x1,x2,…,xn)是划分系统任务流图的一个可行解，代表对系统的一种划分，xi∈{0,1}，xi=1代表Ri由软件实现，xi=0代表Ri由硬件实现，其中i代表第i个节点, i=1,2,…,n.

定义4划分系统中的任务可由软件实现，也可由硬件实现，但不可同时由软件和硬件实现.

在软硬件划分中将原节点集合R={R1,R2,…,Rn}划分为两个子集，即Q=(Rh,RS)，其中Rh∪RS=R且Rh∩RS=Φ.其中Rh表示任务节点交由硬件实现，RS表示任务节点交由软件实现.

系统划分后总的软件代价、硬件代价分别表示为公式(1)、公式(2).

(1)

(2)

软硬件划分问题：给定一个任务流程图以及软件代价函数s(x)硬件代价函数h(x)和约束C，求解软硬件划分，在满足SR≤C情况下，使得HR最小，即软件在约束范围内使得硬件的代价消耗最小.

x=(x1,x2,…,xn)是划分系统进行划分后的一个可行解，xi=1表示Ri由软件实现，xi=0表示Ri由硬件实现，经过划分后的系统硬件代价h(x)、软件代价s(x)可以分别表示为公式(3)、公式(4).

(3)

(4)

式中si与hi分别表示第i个任务节点交给软件和硬件实现所花费的代价.

将软硬件划分问题形式化描述为公式(5).

(5)

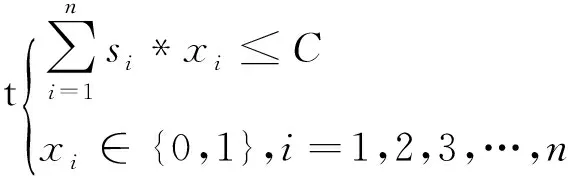
将公式(5)简单变形后得公式(6).

(6)

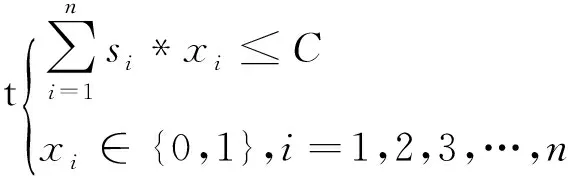
1.20-1背包问题

0-1背包问题(KnapsackProblem)是一种组合优化的NP问题.给定多个重量和价值不同的物品和一个背包，从不同重量和价值的物品中选择装入容量有限的背包使得装入背包中物品的总价值最大.在选择装入背包的物品时，对每种物品i只能选择装入背包或不装入背包，不允许将物品i部分装入背包，也不允许将物品i多次装入背包，在背包问题中假设物品的重量是wi>0,其价值为vi>0，背包的容量为k>0，xi∈{0,1}，当xi=1时表示物品装入背包，否则不装入背包，使得背包所装入的物品重量小于一个背包的容量，即wi*xi≤k,而且要使得背包所装入物品的价值尽量最大化，即使得V=vi*xi达到最大，形式化描述如公式(7).

(7)

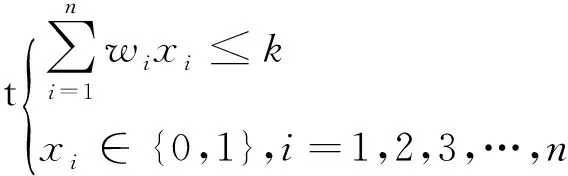
显然，式(7)与式(6)可以进行等价的变换，即将软硬件划分问题的硬件代价hi，软件代价si，约束参数c分别对应0-1背包问题中的物品价值bi，物品重量wi，背包容量k，则说明软硬件划分问题可以看成0-1背包问题进行解决.于是解决0-1背包问题的算法也可以应用到软硬件划分问题.

2　混合蛙跳算法

2.1算法原理

混合蛙跳算法[9](SFLA)是由EusuffM.M和Lansey提出的一种亚启发式群智能进化算法，它的执行过程模拟了一群青蛙在湿地中跳动觅食的自然界元进化行为.该算法的原理为种群中每只蛙代表一个解，湿地代表解空间，在算法的初期，一群蛙被分成m个规模为n的子群，不同的子群.根据适应度值大小找到组内位置最好和最差的青蛙，位置最差的蛙采用一定的进化方法，首先用子群最好的个体与最差的个体产生新的个体，对最差蛙的位置进行调整，可视为一次跳跃，如果新的子个体的适应度比父代个体优，则子个体替代父代个体，否则利用全局最优的个体与最差的个体产生新的个体，可视为再次跳跃，如果新的子个体的适应度比父代个体优，则子个体替代父代个体，否则将随机产生新个体替代最差的个体.在达到预先定义的局部搜索迭代次数之后，这一过程不断重复直到预先定义的收敛条件得到满足.

2.2算法描述

设SFLA算法的第t代种群P(t)的规模为N，分为m个规模为n的子群为Pk(t)(1≤k≤m)，N=m*n，每一只青蛙的个体表示为xi(t)=(xi1(t)，xi2(t),…,xid(t))，(l≤j≤d)其中下界为L=(l1,l2,l3,…,li)，上界为U=(u1,u2,…,ui)，(1≤i≤N)，设xb(t)和xw(t)分别为子群pk(t)的最优个体和最差个体，xg(t)为种群p(t)的全局最优个体，令temp=(y1,y2,…,yd)为一临时向量，R1为(0,1)中的一个随机数，R2为(0,1)中的一个随机数，c1,c2为(1,2)的一个随机数，w为1.17.算法的实现流程如下：

Step1：参数初始化.确定蛙群的数量、种群以及每个种群的青蛙数.

Step2：随机产生初始蛙群，计算各个蛙的适应值.

Step3：按适应值大小进行降序排序并记录全局最优解xg(t),子群最优解xb(t)和最差解xw(t).

Step4：根据种群P(t+1)个体f(temp.a[i])的值降序重新排列，重新构成子群Pk(t+1)(1≤k≤m)并对其进行评估，更新子群中的xb(t+1),xw(t+1), xg(t+1).

Step5：输出xg(t).

3　仿真实验

实验环境为32位Windows7，CPU：Intel(R)Core(TM)i5-3470，RAM：4.00GB，所使用的编程语言为C++.

由于嵌入式系统软硬件划分问题可以建模转换成0-1背包问题，那么应用于0-1背包问题的测试基准同样适用于软硬件划分问题.本文分别给出3个实例，其中实例1、2选自文献[12]，实例3选自文献[7].

实例1i=10，c=269，硬件代价hi={55,10,47,5,4,50,8,61,85,87}，软件代价si={95,4,60,32,23,72,80,62,65,46}.

回溯算法和e-近似算法[11]可解得到最优值295，蚁群算法则要迭代100多次以后可得到最优解，运行人工萤火虫群算法[12]，迭代20次后得到最优解，运行混合群算法，迭代2次就可以得到最优解.与蚁群算法对比结果如图1所示：

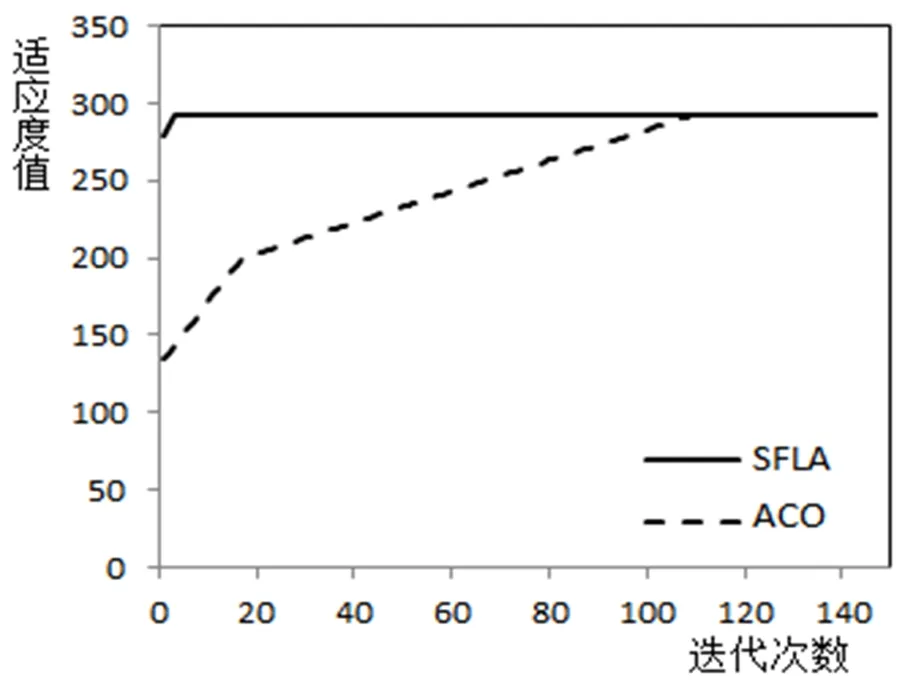
图1　SFLA与ACO算法收敛性图

实例2i=20，c=878，硬件代价hi={92,4,43,83,84,68,92,82,6,44,32,18,56,83,25,96,70,48,14,58}，软件代价si={44,46,90,72,91,40,75,35,8,54,78,40,77,15,61,17,75,29,75,63}

回溯算法解得最优值为1024，e-近似算法解得近似值1018，蚁群算法和蜂群算法可得到的最好解为1024，文献[7]采用蚁群算法求解，经过200次迭代得最优解为1024.运行蜂群算法，60次迭代后可得最好解为1024，采用本文提出的混合蛙跳算法只需28次迭代即可得到最优解1024.与蜂群算法的对比结果如图2所示：

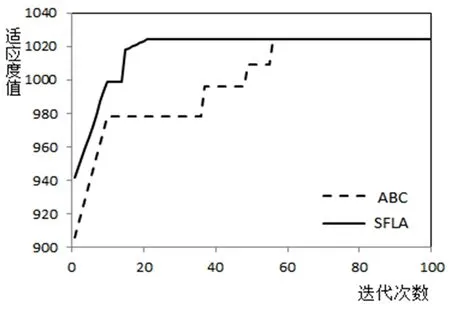
图2　SFLA与ABC算法收敛性图

实例3i=20，硬件代价hi={91,2,43,83,84,85,65,96,87,8,49,30,19,58,87,26,95,74,43,12,51}，软件代价si={41,42,93,74,95,46,77,38,9,50,79,48,77,16,65,14,73,22,71,60}，对比粒子群算法和混合蛙跳算法得如表1所示.

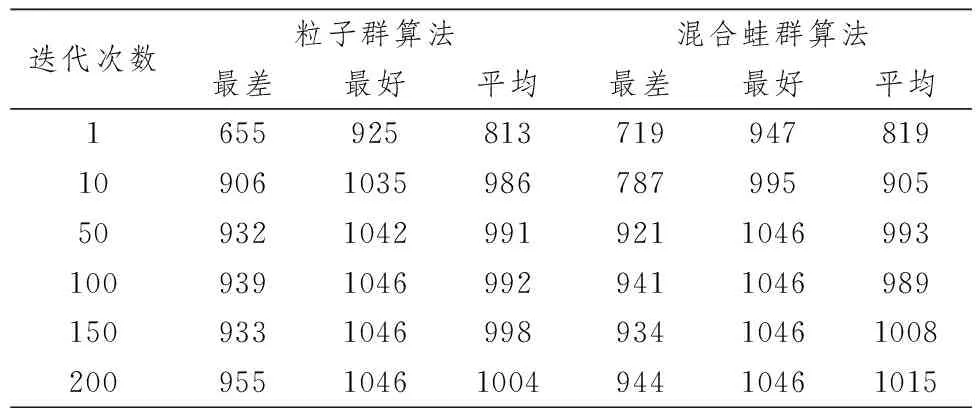
表1　不同方法在实例3上的统计结果

对比表1中的统计数据可以得出，迭代次数范围在1～100之间，运用粒子群算法和混合蛙跳算法求得0-1背包问题最优值相近，迭代次数为100～200范围内，混合蛙跳算法求得的0-1背包问题最优值明显优于粒子群算法.

4　结语

借鉴解决0-1背包问题的思路，结合混合蛙跳算法的优势，本文提出了一种基于混合蛙跳算法求解软硬件划分问题的新方法.实验表明，该方法具有可行性和有效性，在工程实际中有一定的应用价值.下一步的研究工作是进一步改进该算法，拓宽该算法的应用领域.

[1]P.Arato, S.Juhasz, Z.A.Mann. Hardware- software partitioning in embedded system design[A].WISP2003,Budapest,Hungary,Septem-ber 2003:197-222.

[2]R. K. Gupta. Co-synthesis of hardware and software for digital embedded systems[D].PhD thesis, Stanford University, December 1993.

[3]R.Ernst,J.Henkel,T.Benner.Hardware-software co-synthesis for micro-controllers[J]. IEEE Design Test Comput.1993,10(4):64-75.

[4 ]刘功杰，张鲁峰，李思昆.遗传算法在软硬件划分中的应用[J].国防科技大学学报.2002,24(2):64-68.

[5] 邹谊，庄镇泉，李斌.基于量子遗传算法的嵌入式系统软硬件划分算法[J].电路与系统学报,2004,9(5):1-7.

[6]R.Guo,B.Li,Y.Zou,Z.Zhuang. Hybrid quan turn probabilistic coding genetic algorithm for large scale hardware-software co-synthesis of embedded system [J].IEEE Congress on Evolutionary Computation,2007:3454-3458.

[7]FARMAHINI-FARAHANIA,KAMALA,FAKHRAIESM,etal.HW/SW partitioning using discrete particle swarm[C]//Proceed-ingsofthe 17thACM Great Lakes Symposium on VLSI. NewYork:ACM Press, 2007: 359- 364.

[8]刘安,冯金富,梁晓龙,等. 基于遗传粒子群优化的嵌入式系统软硬件划分算法[J] .计算机辅助设计与图形学报, 2010,22(6):927-933.

[9]胥枫,张桂珠,赵芳,等,一种具有领导机制的混合蛙跳优化算法[J].计算机应用研究, 2014(7).

[10]赵洋，单娟.二进制混合蛙跳算法秋季0-1背包问题[J].计算机工程与应用，2010，46(35):39-44.

[11] MA Qiang，YOUNG E F Y．Voltage island-driven floor planning[C]//Proc of IEEE/ACM International Conference on Computer-Aided Design．Piscataway: IEEE Press，2007: 644-649．

[12]程魁，马良.0-1背包问题的萤火虫群优化算法[J].计算机应用研究，2013(4):993-995.

[责任编辑苏琴]

[责任校对黄招扬]

Hardware/Software Partitioning based on Shuffled Frog Leaping Algorithm

LU Chena，MAO Le-lea，HUANG Yongb

(a.CollegeofInformationScienceandEngineering;b.NetworkandInformationManagementCenter,GuangxiUniversityforNationalities,Nanning530006,China)

Hardware and software partitioning is a key problem in the co-design of hardware and software of embedded system, which affects the performance of the system. In this paper, we present a new method based on shuffled frog leaping algorithm(SFLA) for solving the hardware/software partitioning problem, which is formulated as a 0-1 knapsack problem. The SFLA algorithm can keep looking for more optimal feasible solution, and gradually to search the global optimal solution, which makes the minimal total cost of hardware and software development. Experimental results show that our method is feasible for the hardware/software partitioning, and has much better convergence rate than the contrast algorithms.

hardware/software co-design; hardware/software partitioning; shuffled frog leaping algorithm; heuristic algorithm

2015-10-20.

广西高校科学技术研究重点项目(2013ZD021)；广西民族大学2015年研究生教育创新计划项目(gxun-chxs2015097).

卢晨(1991-)，女，江西赣州人，广西民族大学硕士研究生，研究方向：可信系统验证与分析、网络与信息安全；毛乐乐(1989-)，男，河北衡水人，广西民族大学硕士研究生，研究方向：大规模集成电路验证.

TP302

A

1673-8462(2016)02-0073-04