人民币汇率收益率厚尾性研究*

吴慧慧

(岭南师范学院 数学与计算科学学院，广东 湛江　524048)



人民币汇率收益率厚尾性研究*

吴慧慧

(岭南师范学院 数学与计算科学学院，广东 湛江524048)

以2005年7月22日至2015年12月30日的美元兑人民币汇率的每日中间报价作为为研究对象，采用EGARCH模型过滤了收益率序列的非线性特征得到标准化的收益率序列，利用GPD分析方法对标准收益率序列的上下尾部的厚尾性进行了研究.结果表明人民币汇率收益率存在双侧厚尾的风险，且上尾比下尾的尾部风险更大.

人民币汇率收益率;EARCH模型;极值理论;GPD分布法;尾指数

0　引言

金融资产收益率序列的分布往往具有厚尾的特征，表现为超出峰度，即峰度大于正态分布的峰度，超出峰度的存在使得极值事件发生的概率大大增加，从而增加了金融资产的投资风险.进一步认识投资资产具有较大的上厚尾风险还是下厚尾风险对投资组合的选择，资产的定价以及风险管理等等具有重要的实践意义和参考价值：下厚尾风险比较大的金融资产其价格发生下跌的风险较大，多头持有者将面临头寸下跌的风险；上厚尾风险比较大的金融资产价格发生涨幅的可能性较大，多头持有者面临较大的交易对手风险.

对于金融资产收益率厚尾性很多学者做了大量的研究[1-4]，但是对这种厚尾性风险是来自于上厚尾，下厚尾或是双侧厚尾的研究并不多，文章将基于极值理论中广义Pareto分布(GPD)方法对人民币汇率收益率的上下厚尾风险进行实证研究.

1　模型方法介绍

大量研究表明，金融资产的收益率过程一般都存在波动集聚性，条件方差时变性，长记忆性，非对称性等非线性特征，因此，在考察收益率序列的厚尾特征之前有必要使用GARCH类模型对金融资产的收益率序列进行过滤，得到标准化的残差序列，即标准化的收益率序列.对于波动模型的选取，论文选用既放松了对GARCH模型参数非负性约束，又可以反映出杠杆效应的指数GARCH(EGARCH)[5]，相对于其他分布，正态分布具有薄尾的特征，为了不影响原收益率序列的厚尾性，方差方程中条件分布设定为正态分布.EGARCH(1,1)模型方差方程的具体形式设定为：

(1)

其中εt=ztσt，zt～N(0,1),{zt}即为标准化的残差序列，即标准收益率序列.

考察序列{zt}的厚尾性特征，利用极值理论建立尾指数估计量刻画尾分布的肥尾程度，关于尾指数的估计方法主要有块最大值法，广义Pareto分布法(即GPD方法)和Poisson-GPD方法(即POT方法)，论文采用GPD方法进行尾指数估计.

2　GPD模型

广义Pareto分布(GPD)的定义如下：

(2)

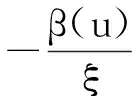
当ξ≥0时，GPD分布是厚尾的，ξ取值越大，说明厚尾性特征越明显[6].

股票和高频外汇收益率，因其存在有限方差，在实证分析中ξ的估计值一般都是小于0.5的[7].

对金融资产的投资者而言，他们更关注的是超过某个门限值u后的金融时序变化情况.

设X1,X2,…,Xn是独立同分布的随机变量，具有相同的分布函数F(x)，对于门限值u，对于超出量Yi=Xi-u的分布为

Fu(y)=P(X-uu)

(3)

超过门限值u的尾部分布可以表示为

1-F(x)=(1-F(u))(1-Fu(y))

(4)

根据历史模拟法，若样本容量为n，且门限值u充分大，则假设Nu表示样本中超过门限值u的样本数量，则

(5)

Pickands研究表明[8]，若门限值u充分大，则Fu(y)～Gξ,β(u)(y)

(6)

对于充分大u，超过门限值u的尾部分布可近似表示为

(7)

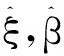
关于门限值u的选择，在实证分析中一般根据QQ散点图，样本均值超过数(MME)散点图和Hill散点图三者结合起来进行确定.

QQ散点图一般是与指数分布进行比较，相对于正态分布的薄尾特征，指数分布具有中等厚度的尾部.关于QQ散点图可参考彭作祥(2006)[9]37-39.

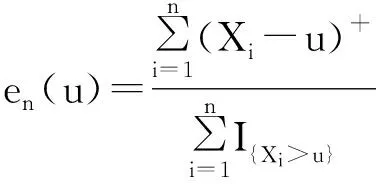
若MME散点图近似为门限u的增函数，则初步估计为厚尾分布，反之，若MME表现近似为水平或向下的直线，则初步估计为薄尾分布.

Hill散点图是根据尾指数ξ的Hill估计量得到的：

(8)

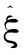
3　实证研究

3.1样本数据的选取及简单分析

2005年7月21日我国人民币汇率形成机制由紧盯美元的固定汇率制改为以市场供求为基础的、顶住一揽子货币的浮动汇率制度.文章选取从2005年7月22日至2015年12月30日间每个外汇交易日美元兑人民币中间牌价作为研究对象，数据来源于国家外汇管理局.

收益率的计算采用对数收益率的形式，汇率中间价序列{Pt}取对数之后进行一阶差分得到序列{Rt}：

Rt=100×(lnPt-lnPt-1)

(9)

对人民币汇率收益率的统计分析，采用的统计量为均值、最大值、最小值、标准差、偏度系数、峰度系数、Jarque-Bera统计量，结果如表1所示，图1为收益率序列的时序图.

表1　收益率的基本统计特征

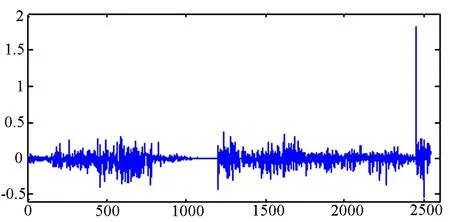
图1　收益率R的时序图

由表1知人民币汇率收益率偏度系数为4.7272，因此收益率数据的分布不是围绕均值对称分布的，存在一定的右偏性；峰度为90.8899，显著的大于正态分布的峰度，存在超额峰度，因此数据的分布显著的存在厚尾的特征；J-B统计量相应的p值为0，说明收益率序列显著的拒绝正态分布的原假设.

由图1可知，汇率收益率波动性从2006年开始逐渐增加，这是我国汇率制度改为浮动汇率制度的结果，到2008年10月份汇率的波动幅度大幅上升，这可能是由于全球金融危机的爆发引起的.2009年到2010年的6月份，汇率的波动幅度相对比较小，但是其后，汇率的波动一直维持着比较大的波动幅度，通过对时序图的分析可知，收益率R的波动存在着明显的集聚特征.

3.2样本数据的处理

由表1所得的收益率的基本特征都是基于收益率序列是独立且同为正态分布的假设下给出的结果，忽略了收益率序列本身的一些非线性特征，如波动过程的集聚性，收益率序列的长记忆性等.所以通过峰度这一简单的统计量去衡量收益率序列的厚尾特征，有可能会高估收益率厚尾风险.论文使用EGARCH (1,1)模型剔除收益率序列的非线性特征得到标准化的收益率序列.

由于GARCH类模型只使用于平稳性数据建模，故首先对收益率序列进行ADF检验，由于收益率序列的均值为-0.0088，故假定收益率序列在0附近波动，ADF统计回归方程中不含常数项和时间趋势项，得到ADF统计量的值为-39.3618，相应的p值为0，故认为收益率序列是平稳的.因此可以使用EGARCH模型对序列进行拟合.

软件Eviews 6.0可得方差方程参数估计的结果如表2：

表2　EGARCH模型估计结果

注：括号内为相应参数估计值的p值

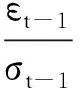
根据模型估计的结果可以得到汇率收益率的标准化残差，即标准化的收益率序列{zt}.

3.3厚尾性检验

论文使用GPD方法对时序的上尾指数和下尾指数进行估计和检验.首先确定门限值u：

由图2中图(a)可知序列的分布上尾相对于指数分布具有显著的厚尾特征，由图(b)可知，在门限值1.5～1.75附近，曲线近似为向上倾斜的直线，进一步通过图(c)发现，在门限值1.715附近，形状参数表现相对稳定，故上尾指数的门限值取为1.715.

同理，由图3(a)可知序列{zt}的分布下尾相对于指数分布也具有显著的厚尾特征，由图(b)可知，在门限值1.8～1.9附近，曲线近似为向上倾斜的直线，进一步通过图(c)发现，在门限值1.842附近，形状参数表现相对稳定，故下尾指数的门限值取为1.842.

门限值确定之后就可以对GPD分布进行参数估计，表3为上尾和下尾参数估计的结果：

表3　参数估计的结果

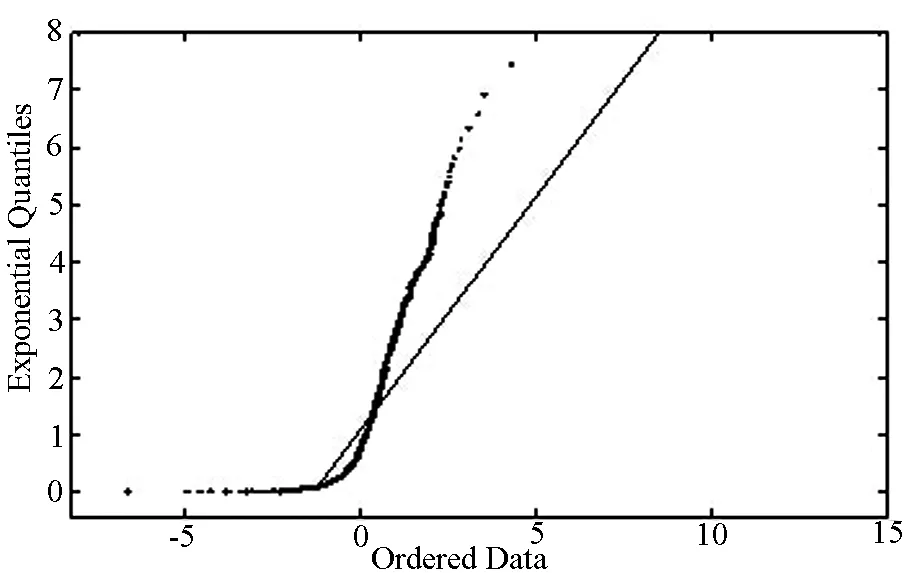
(a) QQ图(与指数分布指数)

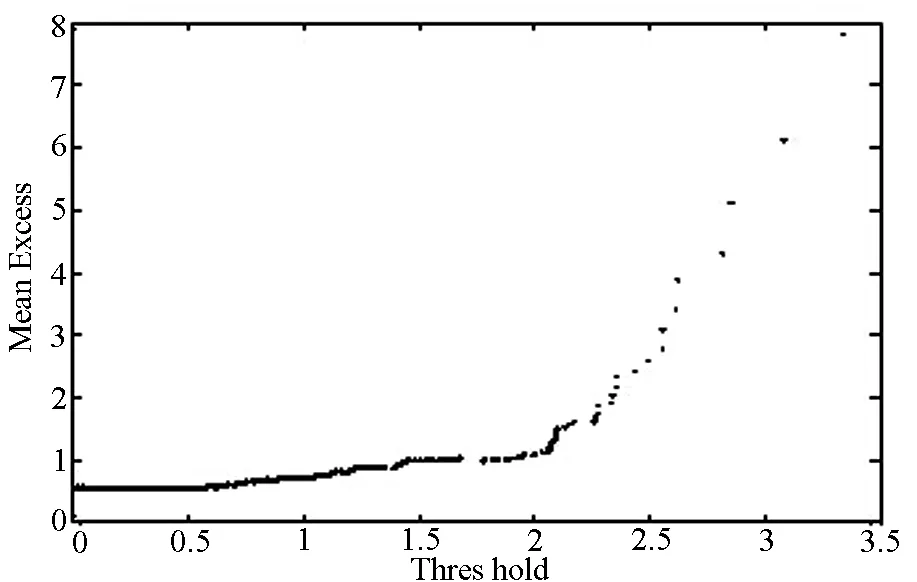
(b) MME散点图

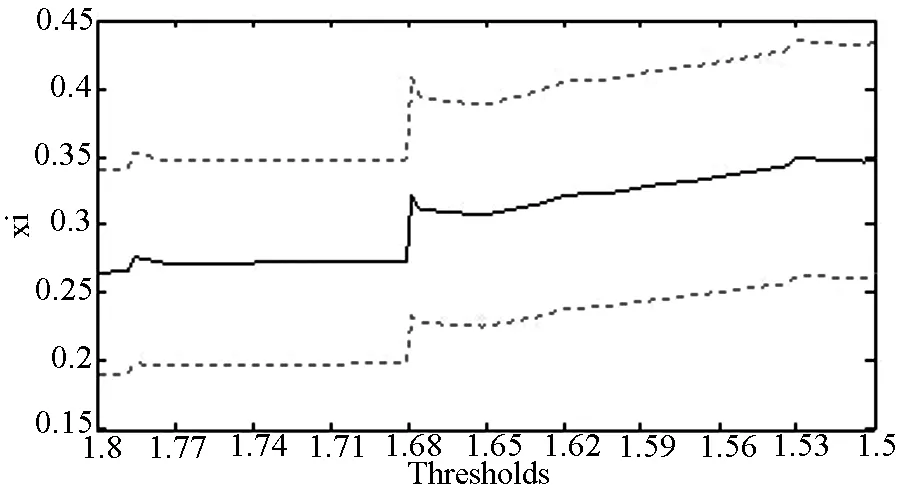
(c) Hill散点图

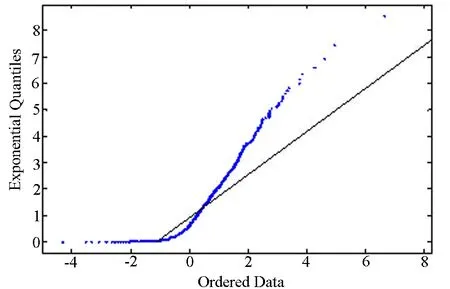
(a) QQ图(与指数分布函数)

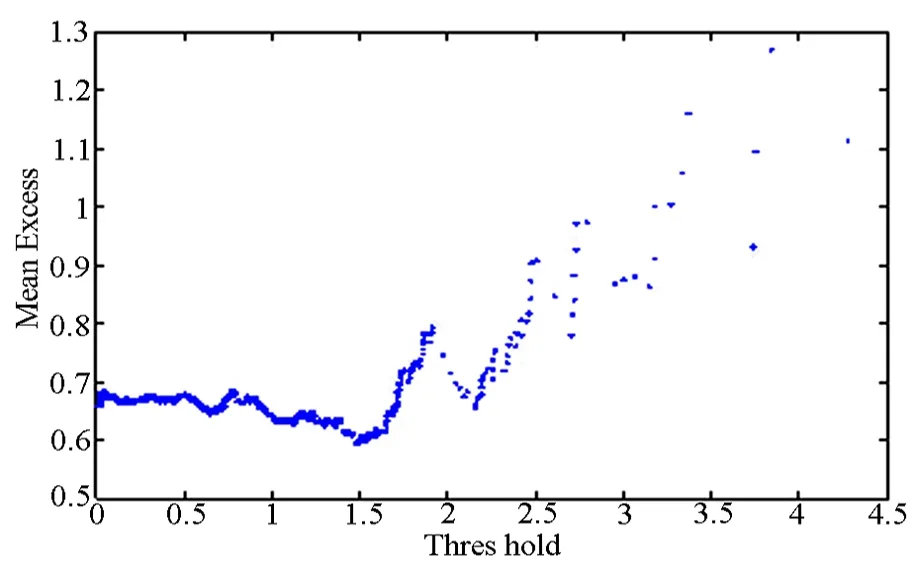
(b) MME散点图

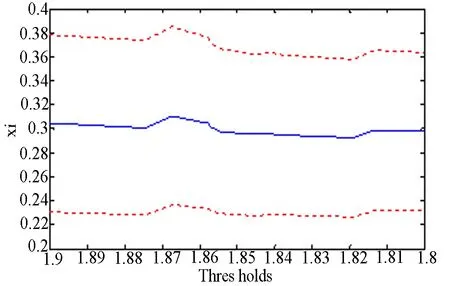
(c)Hill散点图

从估计结果可以看出，序列{zt}的上尾和下尾的形状参数ξ都是显著的大于0的，进一步说明了序列的上尾和下尾都存在厚尾性特征.

关于参数估计的检验，论文采用截断分布拟合、尾分布拟合、残差拟合来完成.

图4和图5分别是时序上尾和下尾模型诊断的检验结果，由图可知参数估计的结果比较理想，且下尾参数估计的结果相对更好.

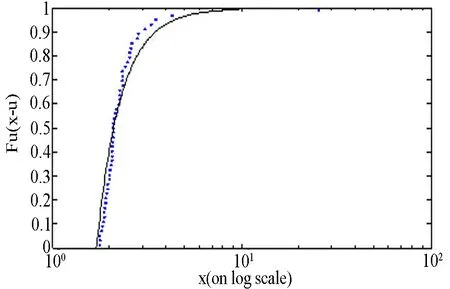
(a) 截断分布拟合检验

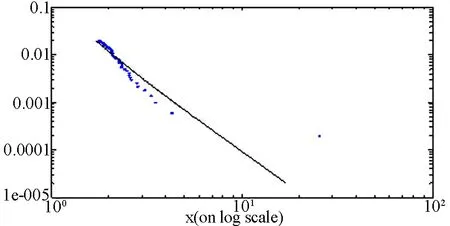
(b) 尾分布拟合检验

(c) 残差QQ检验

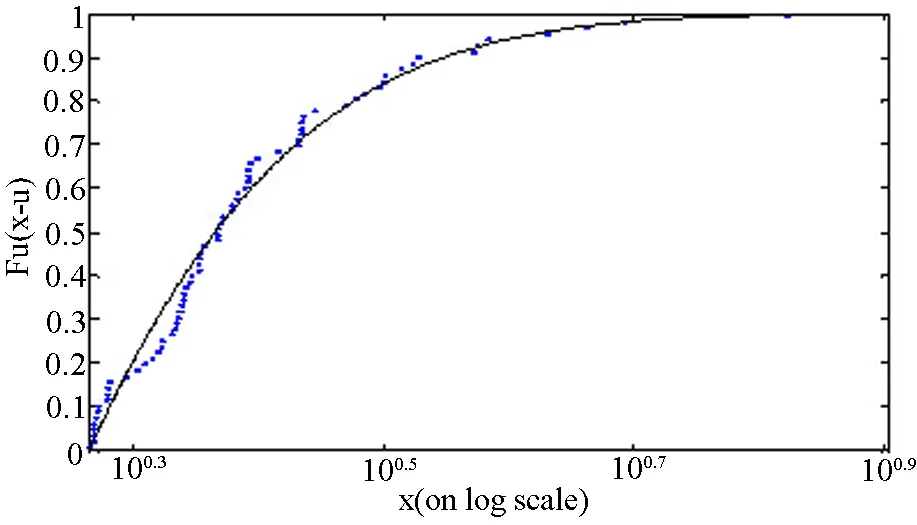
(a) 截断分布拟合检验

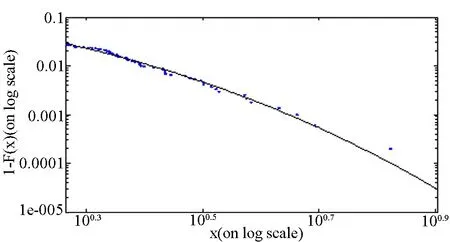
(b) 尾分布拟合检验

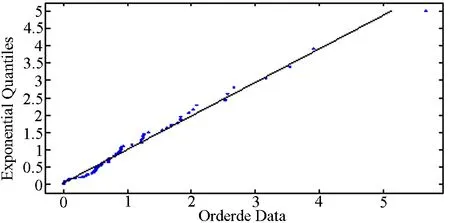
(c) 残差QQ检验

4　结语

人民币汇率标准化收益率存在双厚尾的风险，这说明在剔除了汇率收益率过程中的波动集聚性和杠杆效应等非线性特征之后，人民币汇率标准化收益率出现大幅上涨或大幅下跌的可能性均高于基于正态分布的预测，对于人民币汇率的投资者，无论是做多头还是空头都面临着较大自身风险和交易对手风险.

同时，上尾比下尾的尾部更厚，说明人民币汇率上涨的可能性要大于下跌的可能性，这也与人民币相对于美元贬值的趋势相一致.

[1] 王宗润，吴伟韬，陈超，等. 人民币汇率风险的测度[J] .统计与决策，2009,283(7)：118-120.

[2] 郭燕湄，廖昕，彭作祥. 沪深股市厚尾特征及VAR估计[J] . 西南师范大学学报，2012,37(5):102-106.

[3] Mcneil A J. Estimating the Tail of Loss Severity Distrubution Using Extreme for Insurance and Finance[M] .Berlin：Springer，1997.

[4] Mcneil A，FREY R. Estimating of Tail-related Risk Measures for Heterocedastic Financial Time Series: An Extreme Value Approach[J]. Journal of Emipircal Finance,2000,7(3-4)：271-300.

[5] Nelson D B. Conditional Heteroskedasticity in Asset Returns：A New Approach[J]. Econometrica. 1991,59(2).

[6] 桂文林，韩兆洲，潘庆年. POT模型中GPD“厚尾”性及金融风险测度[J] .数量经济技术经济研究，2010,(1)：107-118.

[7]Ramazan Gencay，Faruk Selcuk . EVIM：A Soft Package for Extreme Value Analysis in MATLAB [J]. Studies in Nonlinear Dynamics and Econometrics, 2001,5(3):213-239.

[8] Pickands J. Statistical inference using extreme order statistics [J]. The Annals of Statistics, 1975(3):119-131.

[9]彭作祥. 金融时间序列建模分析[M] .成都：西南财经大学出版社，2006：37-39，46-48.

[责任编辑苏琴]

[责任校对黄招扬]

A Study on l Heavy Tailed Characteristic of RMB Exchange Rate Return

WU Hui-hui

(SchoolofMathematicsandComputerScience，LingNanNormalUniversity，Zhanjiang524048,China)

The paper make the middle of the daily quotation of the RMB exchange rate against the dollar from July 22, 2005 to December 30, 2015 as the research object, used EGARCH model to filter the nonlinear characteristics of the rate return and get the standardized return series. And then studied the thick tail of the upper and lower tail by GPD analysis method .The result showed that the RMB exchange rate return had double thick tail risk, and the upper thick tail risk was greater.

RMB exchange rate return; EGARCH model; Extreme value theory; GPD distribution; Tail index

2016-03-18.

岭南师范学院校级自然科学青年项目(编号：QL1409).

吴慧慧(1987-),女,山东菏泽人,硕士,岭南师范学院讲师，研究方向：金融数学与金融工程.

F832

A

1673-8462(2016)02-0068-05