溴化锂溶液在亲水水平圆管表面降膜流动的数值模拟

吉　鸽　吴嘉峰　陈亚平　纪光菊

(东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)(东南大学能源与环境学院, 南京 210096)



溴化锂溶液在亲水水平圆管表面降膜流动的数值模拟

吉鸽吴嘉峰陈亚平纪光菊

(东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)(东南大学能源与环境学院, 南京 210096)

为了研究润湿性对水平管外降膜流动性能的影响,基于有限元法建立二维两相流模型,模拟了溴化锂水溶液在水平圆管外亲水表面不同润湿性(静态接触角0°～60°)的降膜流动过程;探究了液体在不同润湿性的水平圆管外壁铺展成膜的瞬态特性;分析了稳定后液膜厚度和液膜表面速度的分布特征．结果表明:当水平管外壁润湿性降低或静态接触角增加时,液体在水平管外铺展成膜所需的时间增加,液膜最前端液体的堆积量增大;达到稳定状态后液膜厚度沿周向呈先减小后增大,液膜速度沿周向呈先增大后减小的变化趋势;液膜最小厚度或最大速度位于周向角120°左右;根据液膜厚度沿周向角分布模拟值与实验数据的比较结果,对Nusselt液膜厚度表达式进行了修正．

润湿性;降膜;水平圆管;瞬态特性;液膜厚度

水平管外降膜流动以其传热温差小、传热效率高、设备成本低等特点,被广泛应用于制冷、海水淡化、化学、石油加工、脱盐等工业领域[1]．

早在1916年,Nusselt[2]对降膜流动进行了理论研究;Hou等[3]在实验的基础上,考虑了管间距对水平圆管外降膜流动特性的影响;何茂刚等[4]实验探究了水平管外降膜流动的液膜最薄点的位置;Killion等[5]研究了在重力作用下水平管外降膜流动管间流形的变化;Bustamanate等[6-7]实验观察了水平矩形管外降膜及管间液滴的流形变化,并数值模拟了溴化锂溶液在降膜流动过程中的传热传质特性．

溴化锂浓溶液降膜吸收水蒸气的过程集流动、吸收、传热于一体,是目前吸收式制冷研究的热点之一．汪磊磊等[8]实验研究了溴化锂溶液液滴在水平管间的形成过程,提出了不同溶液流量下液滴的发展预测曲线;Kyung等[9]将溴化锂溶液在水平管束间的降膜流动分为水平管外降膜、水平管底端液滴的形成和管间流动3个区域,模拟分析了3个不同区域的吸收特性;易哲宇等[10]进行了溴化锂溶液在管排和V形丝网填料交替结构中流动的可视化实验．

为了探究润湿性对瞬态降膜吸收过程的影响,本文建立二维两相流模型,模拟了溴化锂溶液在不同润湿性的水平管外壁的降膜流动过程,分析了润湿性的变化对液膜铺展的瞬态特性和达到稳定状态后液膜厚度的影响．

1　数值模拟方法

1.1模型描述和数学建模

为了使模拟结果具有普遍性和实用性,气相选用40 ℃的干饱和水蒸气,液相选用入口参数为40 ℃、质量分数为60%的溴化锂水溶液,对水平圆管外降膜流动过程进行模拟．选用80 mm×30 mm的矩形作为模拟区域,如图1(a)所示．水平管的外径为φ25 mm,为了减少计算内存和节省计算时间,根据对称性原理对模型的半流域进行模拟,在模型的左上侧开一个1 mm的狭缝作为溶液入口,溶液入口至管子上沿的距离为5 mm．溴化锂溶液从左上侧的狭缝进入模拟区域后,在重力和惯性力的作用下冲刷水平管,在水平管外铺展成一层液膜,溶液达到模拟区域底部后从最下端的出口流出．

采用水平集方法建立二维两相流模型,对溶液在水平管外的降膜流动过程进行模拟分析.水平集函数可表示为[11]

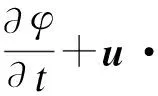
(1)

式中,φ为水平集界面函数,在0～1之间取值,φ=

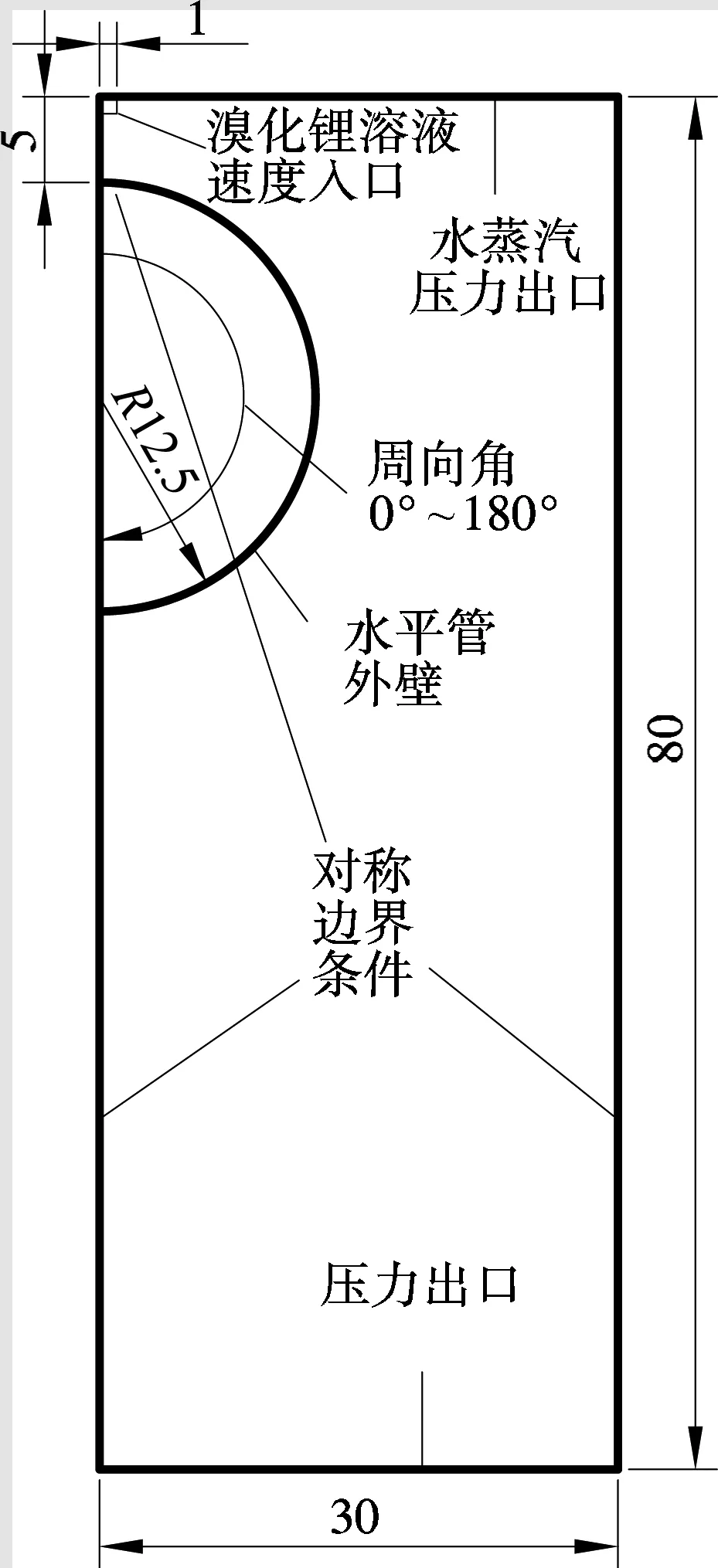
(a) 计算模型和边界条件(单位:mm　(b) 二维网格分布

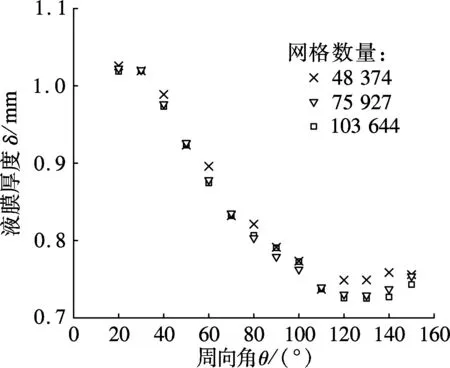
(c) 不同网格数量下液膜厚度随周向角的变化

0为水蒸气相,φ=1为溴化锂溶液相,φ=0.5为溴化锂溶液和水蒸气的界面;u为速度矢量;γ为初始化参数,可根据界面移动速度和收敛性进行调整;εls为界面厚度控制参数,用于控制液相和气相界面的厚度．速度场u可以通过求解动量方程和质量方程获得．

流场中溴化锂溶液和水蒸气可以作为不可压缩流体进行模拟,动量方程和质量方程为

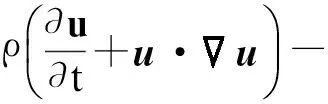
(2)

(3)

式中,ρ和μ分别为密度和动力黏度;P为压力;Fst为表面张力;g为重力加速度．

采用函数φ对界面处的密度和动力黏度进行平滑处理,在界面处

ρ=ρv+(ρl-ρv)φ

(4)

μ=μv+(μl-μv)φ

(5)

式中,下标v表示水蒸气相;l表示溴化锂溶液相．

表面张力Fst的计算式为

(6)

式中,σ为溴化锂溶液的表面张力系数;I为单位矩阵;n为界面法向向量,即

(7)

χ为界面不为0的函数,用下面的表达式计算:

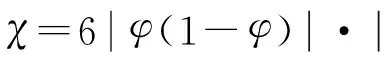
(8)

通过求解质量方程和动量方程得出速度场,将速度场代入水平集函数求出φ,就可以得到不同时刻溴化锂溶液相和水蒸气相的界面,进而得出溴化锂溶液在水平管外的分布．

1.2边界和初始条件

温度为0 ℃、质量分数为60%的溴化锂溶液采用速度入口,入口的平均速度为0.35m/s,入口处溴化锂溶液的体积分数为1．水蒸气相采用压力入口,入口的表压为0Pa,模型的左侧和右侧为对称边界．水平管外壁为润湿壁面,壁面的静态接触角在0°～60°范围内变化,通过改变壁面静态接触角来调整水平管外壁的润湿性．在模拟区域的最下端采用表压为0Pa的压力出口．模拟区域的体积力为重力,重力的方向与溴化锂溶液的流动方向一致．

在初始时,水蒸气布满了整个模拟区域,溴化锂溶液以入口速度0.35m/s、体积分数为1进入模拟区域,在重力和惯性力的作用下向下流动．

此外,当0 ℃、质量分数为60%的溴化锂溶液以0.35m/s的平均速度从1mm的狭缝流入模拟区域时,水平管外单侧单位长度溴化锂溶液的质量流量Γ为0.6kg/(m·s),液膜雷诺数和伽利略数分别为

(9)

(10)

以雷诺数Re和伽利略数Ga为准则数的光滑水平圆管管间流型膜状流的判别式为[12]

Re>2.008Ga0.22

(11)

此时可以得出Ga=7.94×107,Re=369.2.

由于Re>2.008×(7.94×107)0.22=109.8,可见算例的管间流型位于膜状流区,避免了液膜断裂、流型不稳定等因素对管外液膜厚度造成的波动．Nusselt[2]的经典解也假设了液膜的管间流型为膜状流,故本文选用管间流型为膜状流可以将模拟结果与Nusselt解进行分析比较．

1.3网格划分和模型校验

采用三角形网格对模拟区域进行离散化处理,为了提高计算过程的收敛性和计算精度,对溴化锂溶液入口、水平管外壁附近、水平管下端预测溶液会流过的区域和模型出口进行了加密,模型的网格分布如图1(b)所示．在网格划分的基础上,采用有限元法对水平集函数、动量方程和质量方程进行了求解．

为了检验计算结果对网格的依赖性,分别选取数量为48 374,75 927和103 644的网格,模拟了相同边界条件下溴化锂溶液的降膜流动过程,图1(c)为达到稳定状态后3种不同网格数量下液膜厚度δ沿周向角θ的分布．当网格数量超过75 927后,网格的疏密对模拟结果的影响不大,故选用网格数量为75 927进行后续计算．

2　结果分析

2.1液体铺展成膜的瞬态特征

溴化锂溶液通过管子上方的狭缝进入计算流域后,在重力和初始速度的作用下向下流动,接触到水平管外壁后沿壁面流动,在壁面上铺展成膜．图2为水平管外壁润湿性不同时液体铺展成膜的

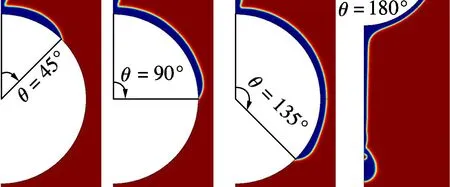
(a) 静态接触角ψ=0°

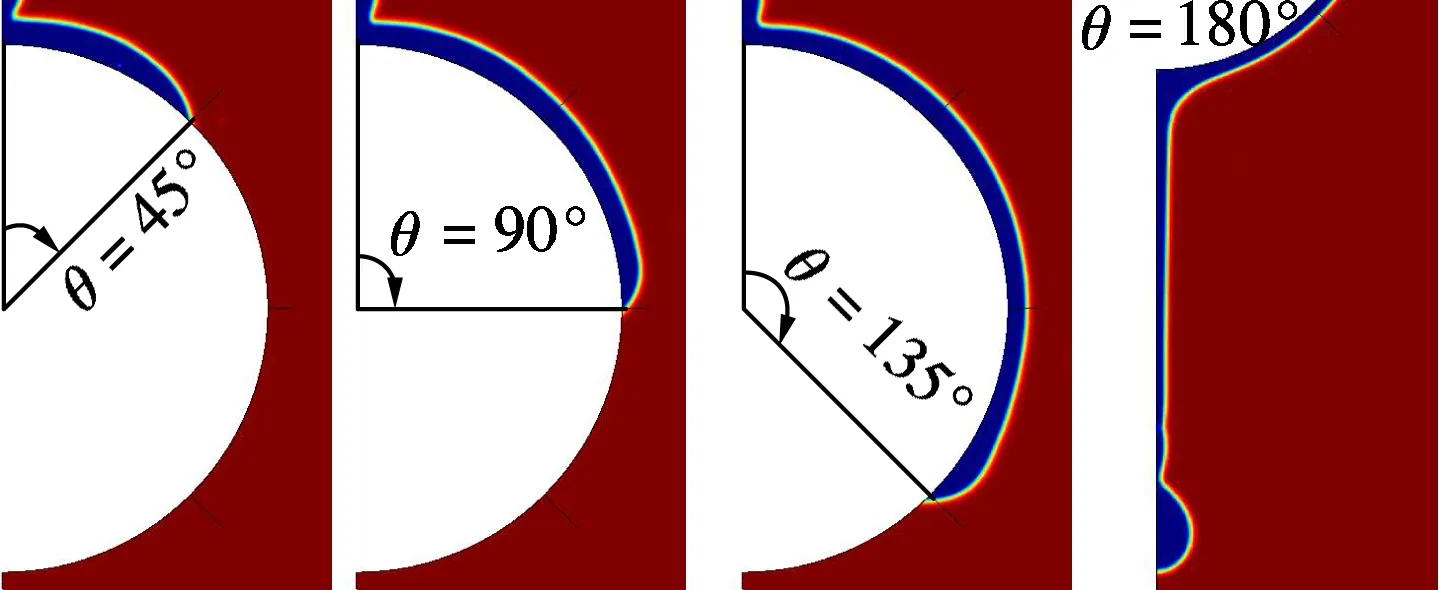
(b) 静态接触角ψ=20°

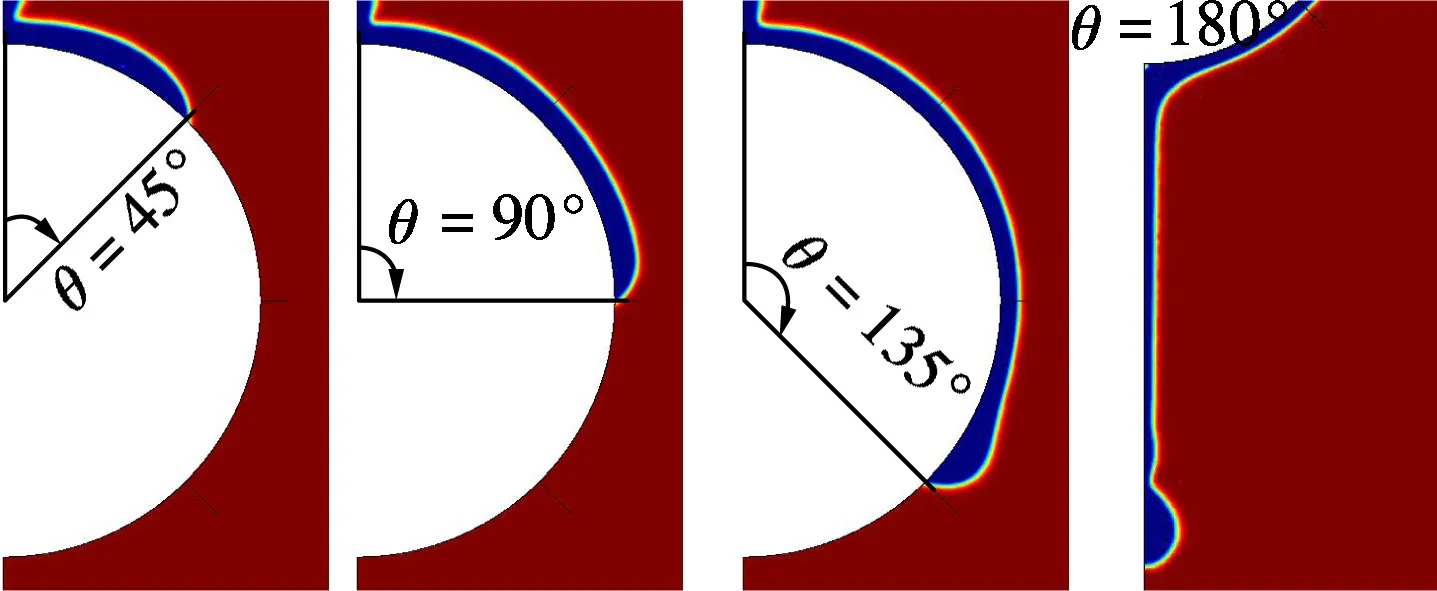
(c) 静态接触角ψ=40°

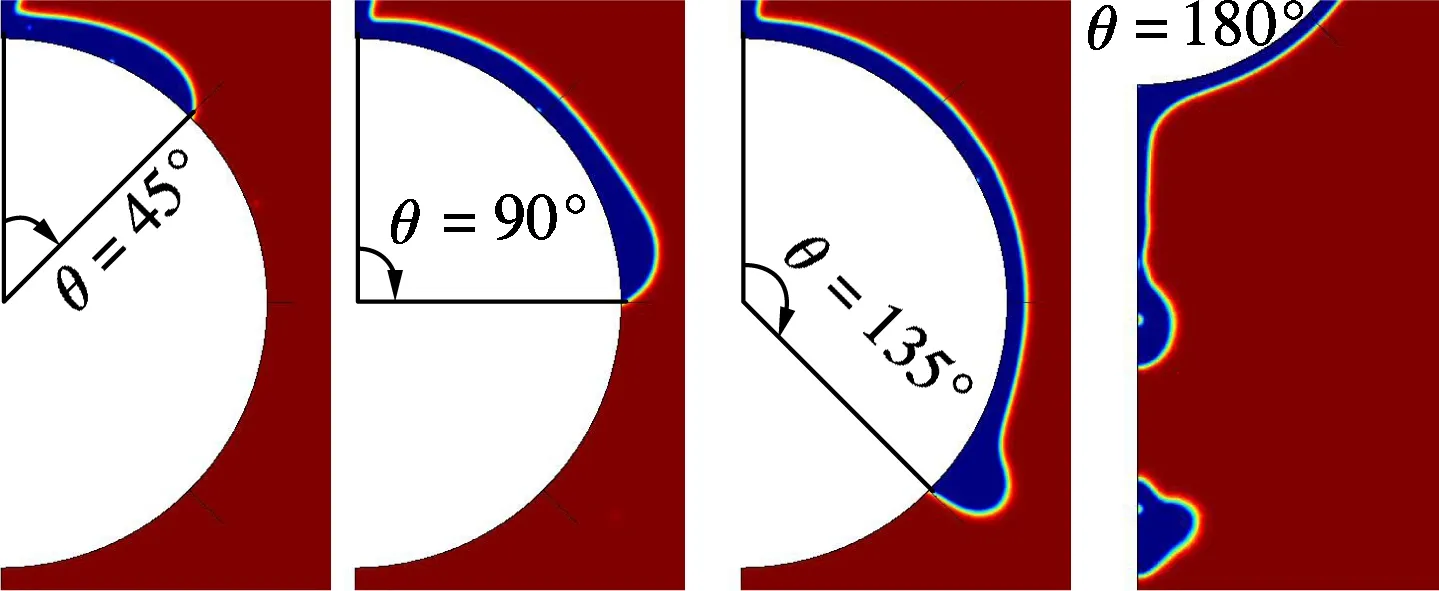
(d) 静态接触角ψ=60°

瞬态局部特征．图中，蓝色部分表示溴化锂水溶液,红色部分表示水蒸气．

由图2可见, 水平管外壁的静态接触角ψ增大或润湿性减弱时, 液膜最前端液体的堆积量增加,而且同一润湿性下,液膜前端液体的堆积量随着周向角θ的增加而增大．液膜铺展的速度也与水平管外壁静态接触角的大小有关,静态接触角增加时,液膜的铺展速度减慢,图2中静态接触角为60°和0°时液膜铺展到周向角135°处所需的时间分别为0.115和0.1 s．

2.2润湿性对布液形态的影响

通过模拟发现,水平管外液膜的前锋线与管外壁固液接触线之间的夹角随着水平管外壁静态接触角和周向角的不同而发生变化,液膜最前端的液气接触线与固液接触线之间的夹角是液膜与壁面接触的一个瞬态角度,定义为动态前进接触角α．不同静态接触角ψ下液体铺展成膜时α角随周向角θ的变化如图3(a)所示．静态接触角相同时,随着周向角θ的增加,液膜在铺展过程中的α角逐渐增大,静态接触角为60°时,周向角160°处与20°处的α角相差35°左右．在同一周向角处,随着静态接触角ψ的增加,液膜的α角逐渐增大,周向角越大,静态接触角的变化对α角的影响也越大．α角与液膜最前端液体的堆积量呈正相关,α角越大,液体在铺展成膜时液膜最前端的堆积量越大．

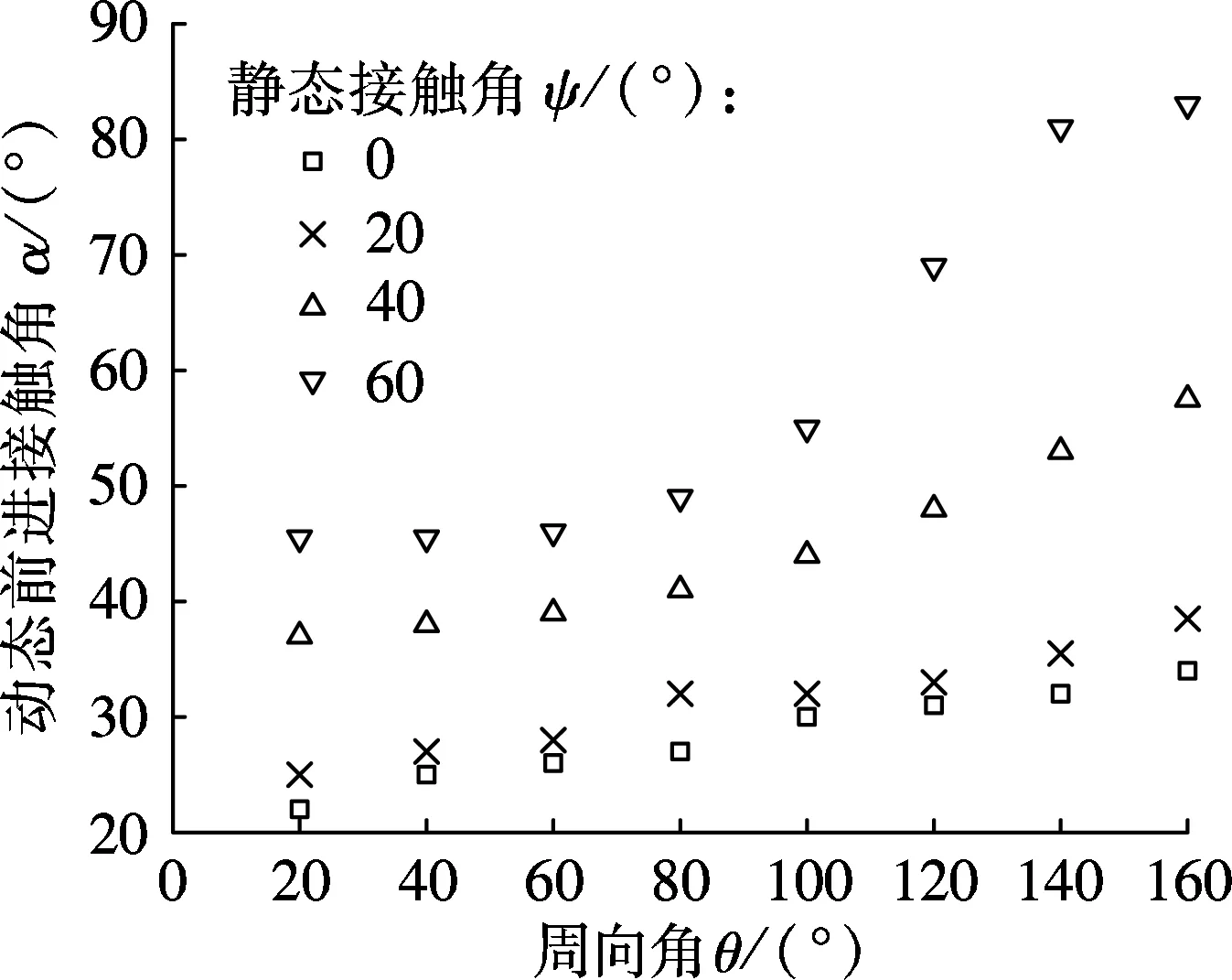
(a) 动态前进接触角α

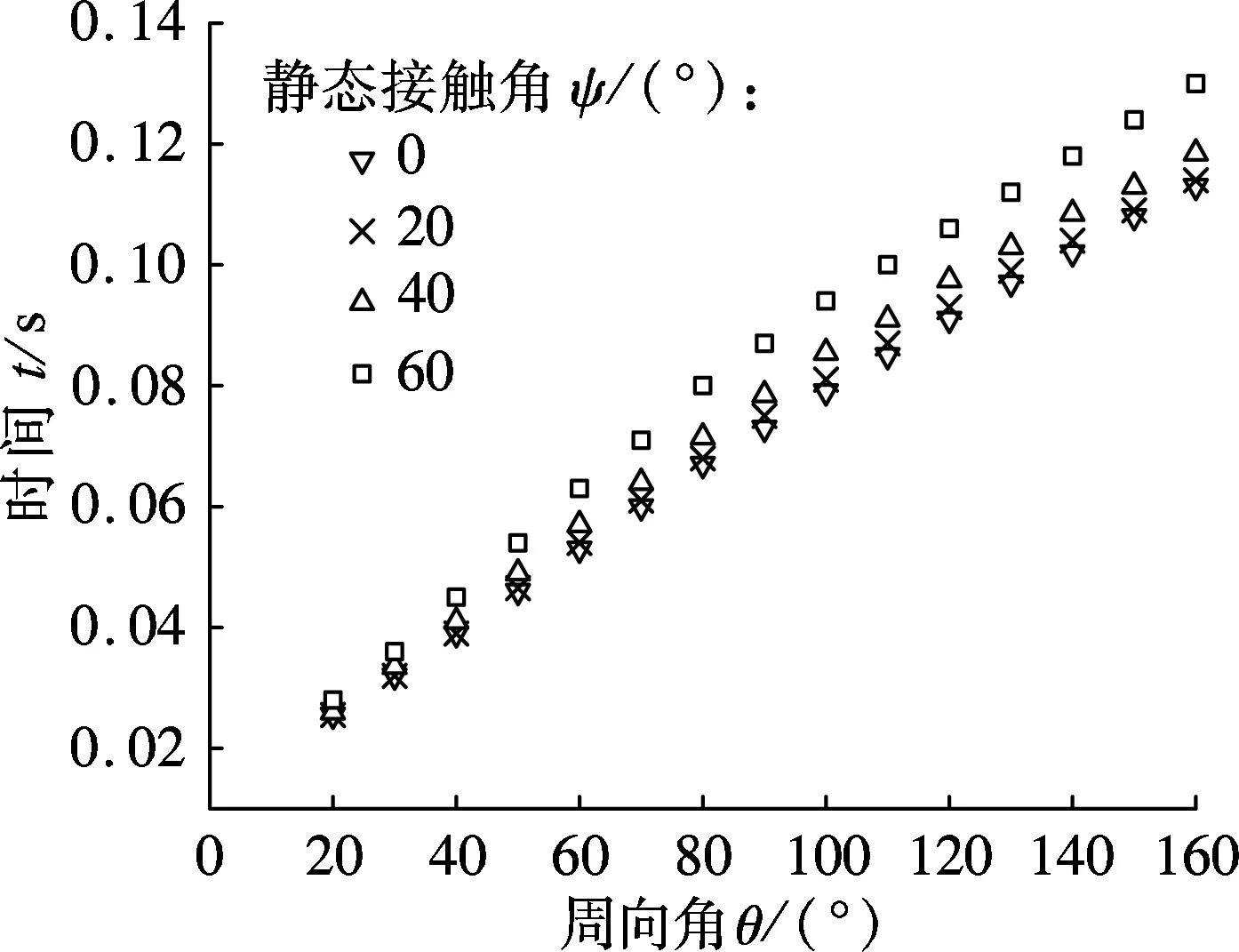
(b) 液膜铺展所需时间

水平管外表面不同静态接触角下液膜铺展所需的时间t随周向角θ的变化关系如图3(b)所示．静态接触角越大,液膜铺展到同一周向角处所需的时间越长,在其他条件相同的情况下,水平管外表面的静态接触角分别为0°和60°时液膜铺展到周向角160°处所需的时间分别为0.113和0.13 s．周向角越大,润湿性的变化对液膜铺展时间的影响越大．

溴化锂溶液接触到水平管最顶端后逐渐在水平管外表面铺展成膜,液膜先随着时间波动,最终达到稳定状态．图4为水平管外壁静态接触角ψ分别为0°和60°时不同时间点液膜厚度δ随周向角θ变化的瞬态值．溴化锂溶液在液膜铺展时间为0.125和0.145 s时，在水平管外壁铺展成完整液膜，在液膜铺展时间为0.180和0.200 s时，液膜厚度趋于稳定.当ψ=0°时,刚铺展成的液膜较厚,随着铺展时间的增加液膜逐渐变薄,最终达到稳定状态．当ψ=60°时,刚在水平管外壁铺展成的液膜厚度没有明显的分布规律,随着时间的推移,液膜厚度逐渐波动并趋于稳定．

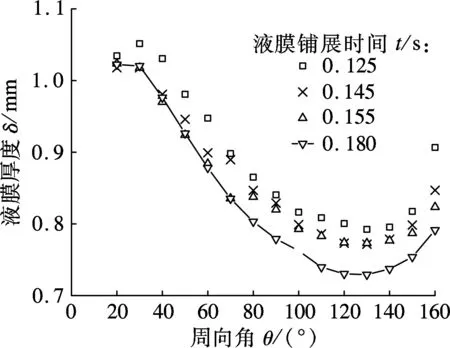
(a) 静态接触角ψ=0°

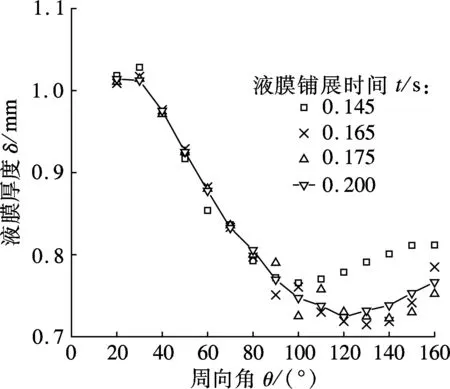
(b) 静态接触角ψ=60°

水平管外壁的静态接触角越大,刚铺展成的液膜厚度分布与达到稳定后的液膜厚度分布越接近,液膜从瞬态到稳定状态的过程中液膜厚度的波动幅度越小.由图4可以看出,当静态接触角为0°时，溴化锂溶液在液膜铺展时间为0.155 s后，只有上半周的液膜厚度趋近稳定状态,而当静态接触角为60°时液膜已几乎全部趋近稳定．

2.3稳态后液膜厚度和液膜表面速度分布

当溴化锂溶液在管外完全铺展成膜且管间流型趋于稳定后,在同一周向角处每隔20 ms读取一次液膜厚度值,3次读取的液膜厚度值误差在0.05 mm范围内时,认为液膜达到稳定状态,并将3次取值的平均值作为稳定后该周向的液膜厚度．图5(a)为静态接触角0°～60°范围内液膜厚度δ沿周向角θ的分布情况．

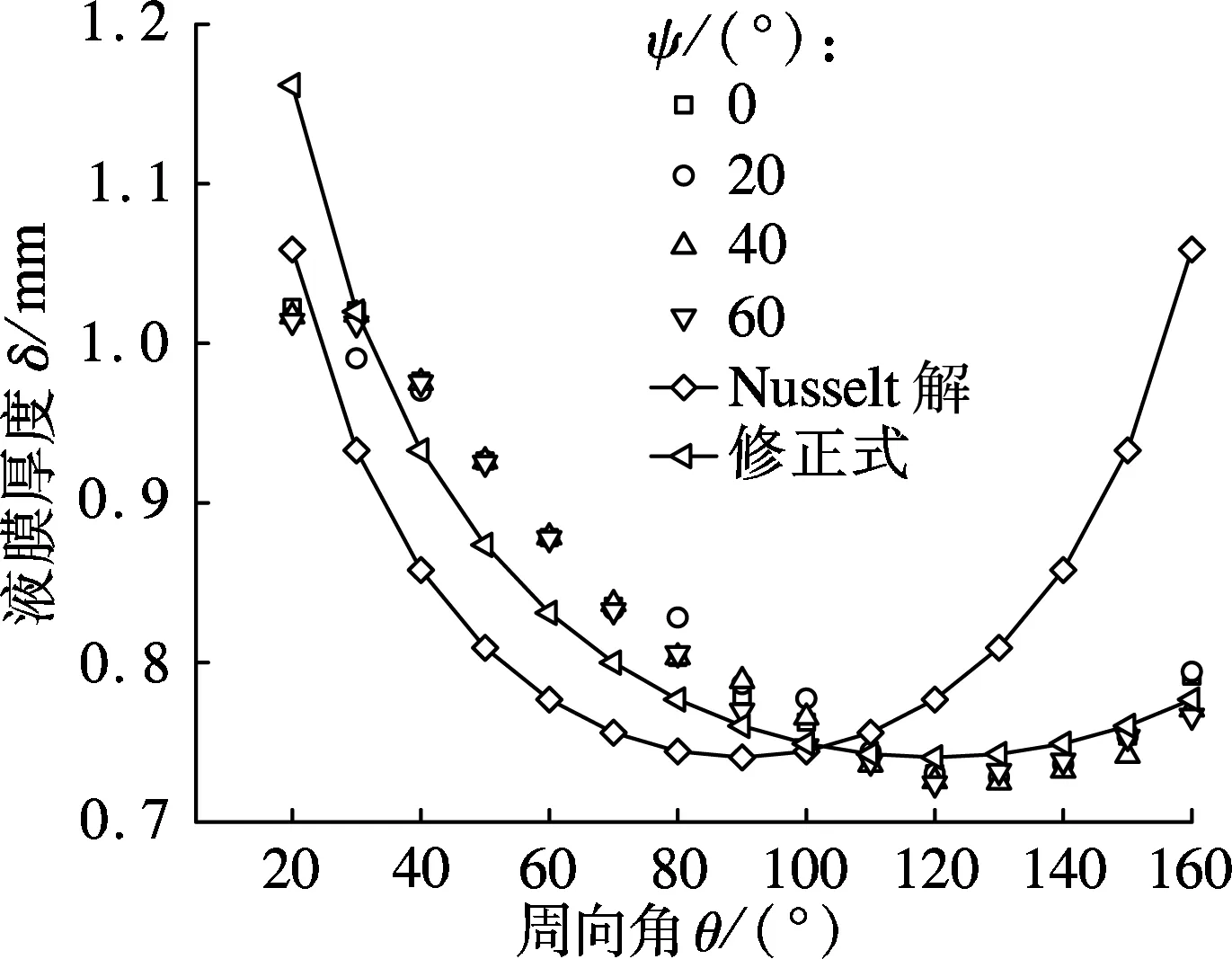
(a) 修正结果与模拟值对比

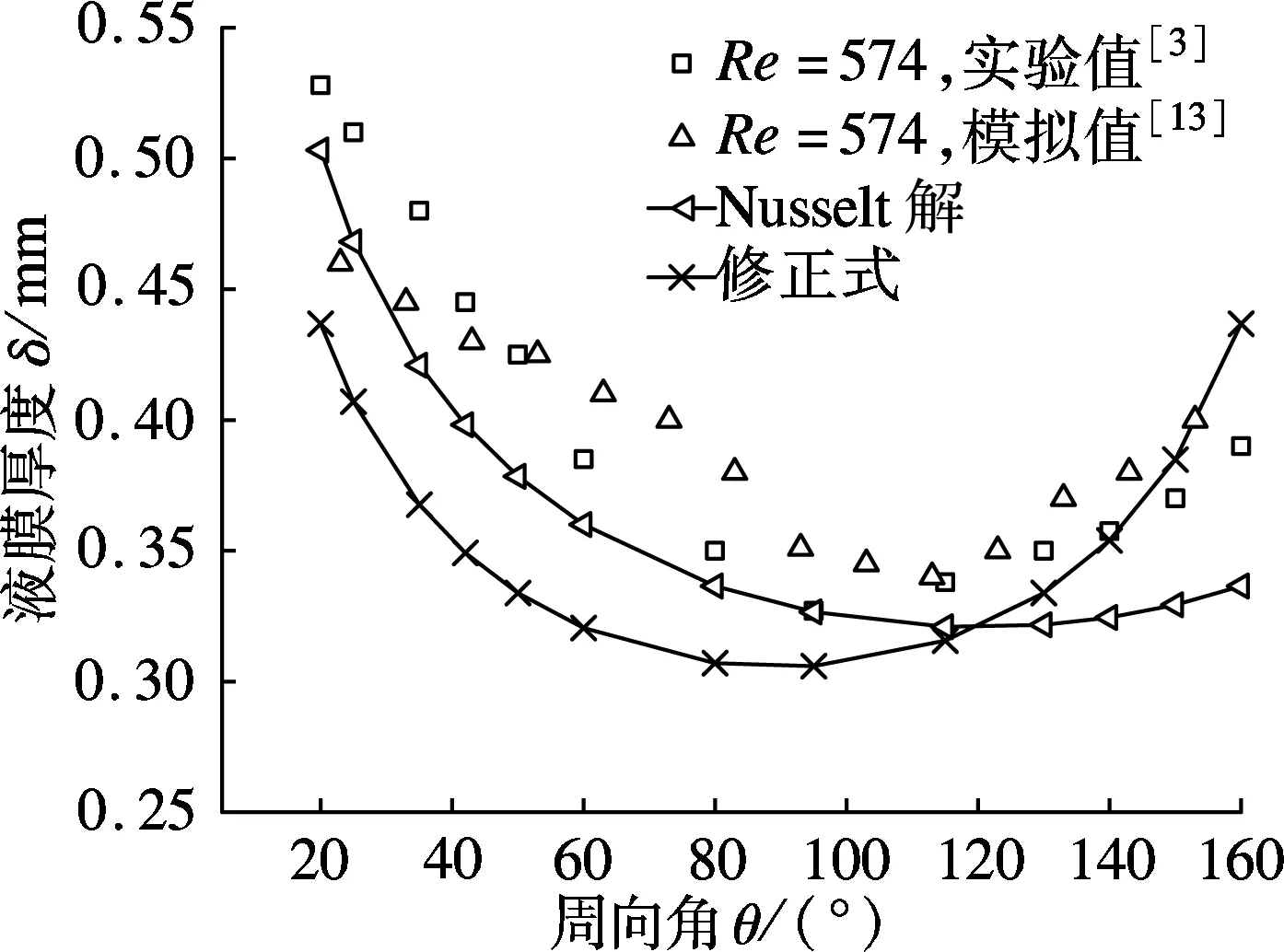
(b) 修正结果与文献[3,12]结果对比

Nusselt[2]在假设液体流动形式为连续的膜状流及忽略了动量对降膜影响的条件下,得出了经典液膜厚度表达式

(12)

由图5(a)可见,同一周向角处水平管外壁静态接触角对稳态液膜厚度的影响不大;液膜厚度沿周向角呈先减小后增大的趋势,这与Nusselt液膜厚度表达式得出的结果基本一致,但由于Nusselt解[2]中忽略了动量对降膜流动的影响,得出的液膜厚度沿周向角呈上下对称的分布趋势,在实际模拟过程中受动量对降膜流动的影响,液膜厚度沿水平管圆周的分布是非对称的[3-4,13]．根据模拟结果,在Nusselt液膜厚度表达式的基础上,考虑动量对液膜厚度的影响,采用周向角θ乘以0.75的方法对液膜厚度表达式进行了修正,即

(13)

图5(a)为不同静态接触角下液膜厚度δ随周向角θ的变化的模拟值、修正表达式(13)及Nusselt解(12)计算结果的比较.由图可见,修正表达式综合考虑了水平管下半周的液膜厚度小于上半周液膜厚度、液膜厚度最小值位于周向角120°左右等特点，因而能够更精确地预测液膜分布.图5(b)为修正表达式(13)所计算的液膜厚度、文献[3]的实验值、文献[13]的模拟值以及Nusselt解的结果比较,可见修正表达式比Nusselt解更接近实验和模拟值．

图6为达到稳定状态后液膜表面速度随周向角θ的变化关系．在周向角120°处,液膜表面速度达到最大值．然后，因重力的切向分力不足以克服黏滞力,故速度逐渐减小．

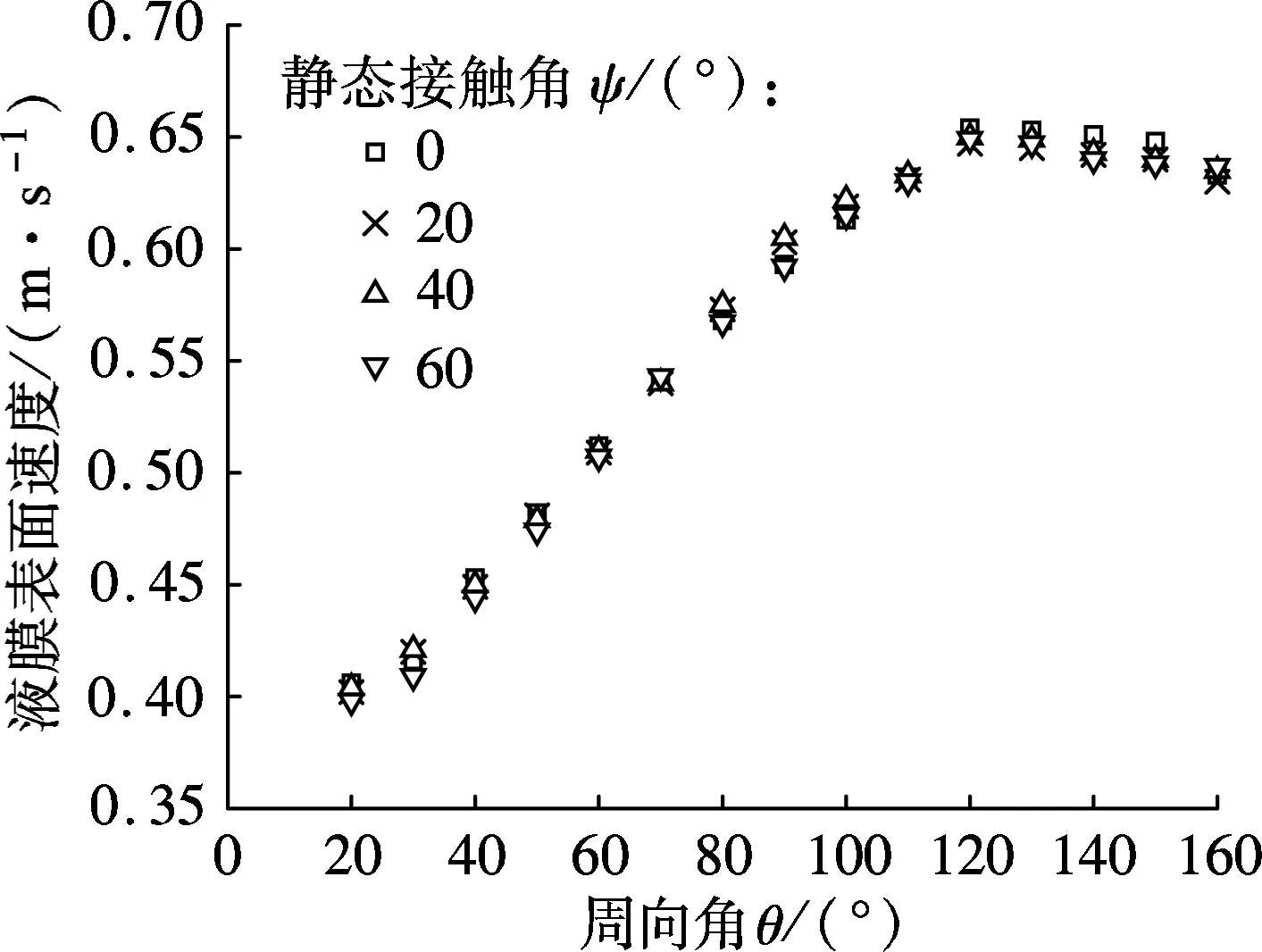
图6　不同静态接触角下液膜表面速度沿周向角变化

3　结论

1) 当水平管外壁的润湿性降低或静态接触角增加时,布液速度减慢,液体铺展成膜所需的时间延长,液膜最前端液体的堆积量增大,不利于降膜吸收；水平管外壁的润湿性越强,溶液在降膜吸收过程中的传热传质性能越好．

2) 在亲水表面范围内,水平管外壁的润湿性越弱,刚铺展成的液膜在达到稳定的过程中厚度的波动幅度越小,润湿性仅影响液膜铺展的瞬态特征,达到稳定后润湿性对液膜厚度和液膜表面速度的影响不大;液膜厚度沿周向角呈先减小后增大的趋势,液膜表面速度和液膜厚度呈相反的变化趋势,液膜最薄处和液膜表面速度最大处均在周向角120°左右．

References)

[1]沈胜强, 梁刚涛, 刘晓华, 等. 水平管降膜蒸发器传热特性研究 [J]. 工程热物理学报, 2012, 33(8): 1391-1394.

Shen Shengqiang, Liang Gangtao, Liu Xiaohua, et al. Heat transfer characteristics in horizontal-tube falling film evaporators [J].JournalofEngineeringThermophysics, 2012, 33(8): 1391-1394. (in Chinese)

[2]Nusselt W. Die oberflächenkondensation des wasserdampfes zeitschr [J].VereinDeutscherIngenieure,1916, 60(2): 541-546, 569-575.

[3]Hou H, Bi Q C, Ma H, et al. Distribution characteristics of falling film thickness around a horizontal tube [J].Desalination,2012, 285: 393-398. DOI:10.1016/j.desal.2011.10.020.

[4]何茂刚, 范华亮, 王小飞, 等. 水平管外降膜流动的膜厚测量和数值模拟 [J]. 西安交通大学学报, 2010, 44(9): 1-5.

He Maogang, Fan Hualiang, Wang Xiaofei, et al. Experimental study and numerical simulation on falling film thickness outside a horizontal tube [J].JournalofXi’anJiaotongUniversity, 2010, 44(9): 1-5. (in Chinese)

[5]Killion J D, Garimella S. Gravity-driven flow of liquid films and droplets in horizontal tube banks [J].InternationalJournalofRefrigeration, 2003, 26(5): 516-526. DOI:10.1016/s0140-7007(03)00009-4.

[6]Bustamanate J G, Garimella S. Dominant flow mechanisms in falling-film and droplet-mode evaporation over horizontal rectangular tube banks [J].InternationalJournalofRefrigeration, 2014, 43: 80-89.

[7]Subramaniam V, Garimella S. Numerical study of heat and mass transfer in lithium bromide-water falling films and drops [J].InternationalJournalofRefrigeration, 2014, 40: 211-226.

[8]汪磊磊, 由世俊, 王书中, 等. 水平管间溴化锂溶液滴状降膜流动分析 [J]. 天津大学学报, 2010, 43(1): 37-42. DOI:10.3969/j.issn.0493-2137.2010.01.007.

Wang Leilei, You Shijun, Wang Shuzhong, et al. Analysis of LiBr solution droplet falling film flow between horizontal tubes [J].JournalofTianjinUniversity, 2010, 43(1): 37-42. DOI:10.3969/j.issn.0493-2137.2010.01.007. (in Chinese)

[9]Kyung I, Herolda K E, Kang Y T. Model for absorption of water vapor into aqueous LiBr flowing over a horizontal smooth tube [J].InternationalJournalofRefrigeration, 2007, 30(4): 591-600. DOI:10.1016/j.ijrefrig.2006.11.001.

[10]易哲宇, 吴嘉峰, 陈亚平, 等. 管排与V形丝网填料交替结构中液膜流动可视化实验 [J]. 东南大学学报(自然科学版), 2015, 45(3): 497-502. DOI:10.3969/j.issn.1001-0505.2015.03.015.

Yi Zheyu, Wu Jiafeng, Chen Yaping, et al. Visualization study on liquid film flow pattern in tubes and V-shaped mesh alternating structure [J].JournalofSoutheastUniversity(NaturalScienceEdition), 2015, 45(3): 497-502. DOI:10.3969/j.issn.1001-0505.2015.03.015. (in Chinese)

[11]Bashir S, Rees J M, Zimmerman W B. Simulations of microfluidic droplet formation using the two-phase level set method [J].ChemicalEngineeringScience, 2011, 66(20):4733-4741. DOI:10.1016/j.ces.2011.06.034.

[12]Hu X, Jacobi A M.Theintertubefalling-filmmodes:Transition,hysteresisandeffectsonheattransfer [M]. Urbana, Illinois, USA: Air Conditioning and Refrigeration Center Press, 1995: 42-45.

[13]Qiu Q G, Zhu X J, Mu L, et al. Numerical study of falling film thickness over fully wetted horizontal round tube [J].InternationalJournalofHeatandMassTransfer, 2105, 84: 893-897. DOI:10.1016/j.ijheatmasstransfer.2015.01.024.

Numerical simulation of falling film flow of aqueous lithium bromide solution over hydrophilic horizontal round tube

Ji GeWu JiafengChen YapingJi Guangju

(Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education, Southeast University, Nanjing 210096, China)(School of Energy and Environment, Southeast University, Nanjing 210096, China)

In order to study the effect of wettability on falling film configuration over horizontal round tube, a two-dimensional two-phase flow model was developed based on the finite element method (FEM) to simulate the falling film configuration of aqueous lithium bromide over hydrophilic horizontal round tube with different wettabilities (static contact angle from 0° to 60°). The transient behaviors of film flow process and the distributions of steady film thickness and velocity along horizontal tube were analyzed in detail. The results show that when the static contact angle increases or the wall wettability decreases, the time spent on film spreading prolongs and the accumulation quantity of the liquid at the forefront of the film increases. The film thickness first decreases and then increases along the circumferential tube surface in the steady-state, while the velocity of the film first increases and then decreases along the circumferential tube surface, the film with the minimum thickness or the maximum velocity appears around circumferential angle of 120°. According to the comparison results between the simulation and the experimental data of the film thickness on a horizontal round tube, a modified correlation based on Nusselt theoretical formula is suggested.

wettability; falling film; horizontal round tube; transient characteristic; film thickness

10.3969/j.issn.1001-0505.2016.04.013

2015-12-21.作者简介: 吉鸽(1992—),女,硕士生;陈亚平(联系人),男,博士,教授,博士生导师,ypgchen@sina.com.

国家自然科学基金资助项目 (51206022, 51276035).

10.3969/j.issn.1001-0505.2016.04.013.

TK124

A

1001-0505(2016)04-0751-06

引用本文: 吉鸽,吴嘉峰,陈亚平，等.溴化锂溶液在亲水水平圆管表面降膜流动的数值模拟[J].东南大学学报(自然科学版),2016,46(4):751-756.