GNSS/INS紧组合算法实时性改进与嵌入式验证

章红平　 常　乐　 汪宏晨　 牛小骥　 高周正,2

(1武汉大学卫星导航定位技术研究中心, 武汉 430079)(2武汉大学测绘学院, 武汉 430079)(3武汉大学科学技术发展研究院, 武汉 430079)



GNSS/INS紧组合算法实时性改进与嵌入式验证

章红平1常乐1汪宏晨3牛小骥1高周正1,2

(1武汉大学卫星导航定位技术研究中心, 武汉 430079)(2武汉大学测绘学院, 武汉 430079)(3武汉大学科学技术发展研究院, 武汉 430079)

针对GNSS/INS实时紧组合导航系统中存在的GNSS数据延迟以及组合更新解算耗时过长的问题,基于Kalman滤波理论,提出了一种在完成了滞后的观测更新后将误差状态向量一步转移到当前时刻的Kalman滤波数学模型.为了验证改进模型的有效性,首先,在Windows平台上,利用车载实测GNSS观测数据和IMU观测数据对比分析了使用改进模型解算与标准Kalman模型解算在GNSS信号中断时段内的导航误差,分析结果表明,2种模型的导航误差相当,说明了改进模型对时间延迟处理的正确性.然后,在DSP硬件平台上,基于改进模型实现了GNSS/INS实时紧组合导航系统,并进行了车载测试,实测结果表明:相对于标准Kalman模型,所提出的改进模型能够在保障紧组合导航系统精度的前提下,将输出导航结果的时间延迟减少到最小,保障了组合导航结果的实时性.

GNSS/INS紧组合;算法实时性;DSP;Kalman滤波

基于全球导航卫星系统(global navigation satellite system,GNSS)和惯性导航系统(inertial navigation system,INS)的组合导航是目前最具有应用价值的组合模式之一,特别是基于GNSS原始观测量和INS数据的紧组合.在该组合模式下,即使在可见卫星不足以单独进行GNSS解算时,仍可有效利用有限的GNSS观测数据和INS数据通过Kalman滤波进行紧组合解算,得到可靠的导航信息[1].因此,GNSS/INS紧组合在工程中得到了越来越广泛的应用.

然而,GNSS/INS紧组合实时应用中,观测数据时间延迟会导致当前时刻观测数据无法实时获取,组合解算时间延迟会导致观测数据无法及时处理,这2个问题直接影响GNSS/INS紧组合系统的实时性能.目前,时间延迟的解决策略主要采用增广状态方法[2]和基于新息重组理论[3-4]建立最优滤波器.其中,增广状态方法会增加状态维度,使得计算量增大;而新息重组的方法,需要建立多个观测方程,如果有多步延迟,则不利于对Kalman滤波器的灵活拓展与应用.而且这些方法只能解决观测数据传输延迟,不能解决计算延迟问题.GNSS/INS实时紧组合算法主要分为机械编排-Kalman预测以及组合更新2部分,前者一般可以在IMU(inertial measurement unit)采样间隔内完成计算;后者则比较耗时,普通嵌入式处理器中无法在IMU采样间隔内及时完成,且GNSS观测数据基本上是从商业接收机板卡中获取,观测数据传输会有一定的延迟,导致Kalman滤波的观测更新计算不能及时完成.这种情况下,如果使用标准Kalman滤波算法,需要将后续IMU观测数据缓存起来不处理,等待观测更新完成才进行下一步计算,这会造成组合导航结果输出的阻塞和延迟,影响系统的实时性能.针对这个问题,本文提出了适用于GNSS观测数据延迟及组合更新计算延迟的Kalman滤波数学模型,并在Windows平台及DSP(digital signal processor)嵌入式硬件平台上对该模型的计算精度和实时性进行了验证和分析.

1　GNSS/INS实时紧组合模型

1.1GNSS/INS实时紧组合数学模型

由于IMU采样率大于GNSS接收机采样率,因此当GNSS观测数据不可用时,GNSS/INS紧组合利用IMU数据通过INS机械编排来更新状态参数中的位置、速度和姿态信息.紧组合系统中,系统状态参数x由INS误差状态和GNSS接收机时钟误差共同组成,可以表示为[1]

(1)

式中,δrn,δvn,ψ分别表示位置误差、速度误差和姿态角误差;bg,sg分别表示陀螺零偏和比例因子;ba,sa分别表示加速度计零偏和比例因子;δVtR表示接收机钟差误差;δfR表示接收机钟漂误差.

采用Kalman滤波时间更新方程实现状态参数的更新[1],即

xk=Φk,k-1xk-1+Gk,k-1wk-1

(2)

式中,Gk,k-1为系统噪声驱动矩阵;wk-1为系统噪声;Φk,k-1为k-1时刻到k时刻的系统转移矩阵,其值由状态参数的动力学模型决定.本文采用Psi角模型来描述位置、速度和姿态的变化[5],采用一阶高斯-马尔科夫过程描述IMU零偏和比例因子的变化[5],采用随机游走过程描述接收机钟差和钟漂的变化[1].

若GNSS观测数据可用,则利用GNSS观测值与INS推算观测量,以闭环修正模式进行GNSS/INS紧组合Kalman观测更新解算,其观测模型可简单表示为[1]

zk=Hkxk+vk

(3)

式中,vk为伪距、多普勒测量噪声;Hk为设计矩阵;zk为观测向量,可通过计算INS推算的GNSS伪距、多普勒值与GNSS接收机观测的伪距、多普勒观测值之差得到,即

(4)

Vioni-Vtropi-PGNSSi

(5)

(6)

式(3)中的Hk可通过对式(5)、(6)进行线性化得到.

1.2GNSS/INS紧组合时间延迟处理

在实时处理中,为了解决GNSS数据获取不及时以及更新计算耗时较长所带来的等待问题,可以将机械编排-预测以及组合更新分解成具有优先级别的2个独立任务进行.处理时序示意图如图1所示,在GNSS采样时刻保存预测误差协方差矩阵和机械编排解算的导航状态,在该采样时刻GNSS观测数据实际接收到的时刻开始进行组合更新计算.在组合更新计算完成后,还需要将滞后计算出的、反映GNSS采样时刻的状态参数估计量以及状态参数协方差估计量正确转移到计算完成时刻(即当前时刻),以修正当前时刻的惯导误差,输出最优的组合结果.在进行这些处理的过程中,应一直保持优先进行INS机械编排和Kalman预测计算.只要保证机械编排-Kalman预测在IMU采样间隔(如5 ms)内完成,以及Kalman观测更新计算在GNSS采样间隔(如1 s)内完成,就能够保证组合导航解算的实时性.

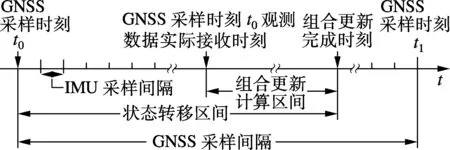
图1　处理时序示意图

1.3状态转移

(7)

根据式(2),并且考虑到Φk+1,k-1=Φk+1,kΦk,k-1,从k时刻迭代到j时刻可以得到

(8)

将式(8)代入式(7),得到

(9)

由式(2)可知,wk-1只影响到xk,所以wi-1(i≥k+1且i≤j)与z1z2…zk不相关,且E(wi-1)=0,因此

(10)

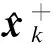
(11)

(12)

(13)

综上,状态转移公式为

(14)

由式(14)可以看出,状态转移可以由累积的状态转移矩阵及状态噪声阵得到,把GNSS采样时刻看作是k时刻,更新计算完成时刻看作是j时刻,利用式(14)可以把k时刻的状态参数更新估计量以及状态参数协方差更新估计量转移到j时刻,进而在更新计算完成时刻进行组合更新.

状态转移矩阵Φ中存在大量零元素,在实时程序中,为了减少计算量,可以对与Φ相关的计算进行专门处理,避免零元素参与乘法运算.

1.4组合更新

采用Kalman滤波进行组合更新解算[6],即

(15)

(16)

在嵌入式系统中,内存资源十分宝贵,为了减少内存开销,本文在嵌入式实时紧组合系统的观测更新中采用了序贯Kalman滤波[8]方式.

2　GNSS/INS实时紧组合系统实现

本文在武汉迈普时空导航科技有限公司高精度定位测姿系统(POS310,IMU主要参数见表1,GNSS板卡型号为Trimble BD982)的基础上,基于TMS320C6747开发了GNSS/INS实时紧组合系统.IMU采样率为200 Hz,GNSS采样率为1 Hz,导航结果输出率为200 Hz,系统设计结构主要有ARM(acorn risc machine)和DSP2个处理器(见图2).ARM负责陀螺仪及加速度计原始数据采集,并利用GNSS板卡提供的1PPS把IMU数据标记上GPS时间标志[9],通过串口向外部和DSP发送带有时间标志的IMU数据,DSP负责实时组合导航的计算.

表1　POS310的IMU主要性能参数

为了实现多任务模式的解算,在DSP中进行了中断优先级和中断嵌套设计[10-12].DSP分为4 kHz定时中断、200 Hz定时中断以及主函数3部分,4 kHz定时中断优先级高于200 Hz定时中断,负责把GNSS,IMU原始数据采集到原始数据环形缓存区[13]中以及把导航结果环形缓存区中的数据通过串口发送到外部;200 Hz定时中断从IMU原始数据环形缓存区中获取IMU观测数据进行机械编排、Kalman预测以及从主函数获取组合更新量进行反馈,再把导航结果存入导航结果环形缓存区中;主函数负责从GNSS原始数据环形缓存区中获取GNSS观测数据进行组合更新计算,并将组合更新量传入200 Hz定时中断.

为了验证算法的实时性能,使用DSP片内计时器统计200 Hz定时中断内从IMU原始数据获取到输出导航结果以及主函数中组合更新的运行时间,并在导航结果中记录输出.

3　实测结果和分析

为了验证GNSS/INS实时紧组合导航系统的性能,本文于2015年9月29日在武汉市文化大道附近进行了2次实际车载测试,每次测试时长约40 min,平均速率为20 km/h,最大速率达38 km/h,测试环境为开阔天空.本次测试使用Trimble Net R9作为静止参考站,基线长度约为16 km,在测试车中搭载本文开发完成的GNSS/INS实时紧组合系统.第1次测试使用本文给出的改进Kalman滤波算法的程序,第2次测试使用标准Kalman滤波算法的程序,同时采集GNSS原始观测数据、IMU原始观测数据以及实时组合导航解算结果.数据分析采用武汉迈普时空导航科技有限公司开发的高精度GNSS/INS组合导航数据处理软件GINS v1.5,使用GINS解算的PPK(post processed kinematic)/INS松组合反向平滑结果作为位置、速度和姿态的参考真值.由于所选路段处于开阔地带,PPK解算均是固定解,在基线小于20 km的情况下,经PPK/INS松组合反向平滑处理后,位置精度为0.05 m,速度精度为0.01 m/s,航向精度为0.02°～0.05°,横滚俯仰精度为0.01°～0.02°,该精度高于常规的GNSS/INS伪距紧组合算法约1个量级以上,因而可以用来评价GNSS/INS实时紧组合导航系统的性能.

3.1延迟处理精度验证

利用采集的原始数据,在Windows平台下采用正向滤波仿真GNSS/INS实时紧组合的方式来验证本文对延迟处理的正确性.对测试时段从GPS历元数260开始到GPS历元数2 660结束,共模拟了14次卫星信号中断,每次中断时长1 min,中断结束后信号恢复2 min,用来恢复状态估计.通过对比在没有延迟GNSS观测数据的情况下,标准Kalman滤波处理方法(方案1)与GNSS观测数据被人为延迟0.9 s的情况下,采用本文提出的改进Kalman滤波处理方法(方案2)在信号中断时段的导航误差,来评估本文方法对时间延迟处理的精度.

2种方案处理的误差曲线如图3和图4所示,图中,ΔPN,ΔPE,ΔPD分别表示位置北、东、地误差,ΔVN,ΔVE,ΔVD分别表示速度北、东、地误差,ΔAR,ΔAP,ΔAH分别表示横滚、俯仰、航向的姿态误差.从图中可以看出,导航误差曲线基本一致.从表2的统计结果来看,方案1和方案2在卫星信号中断期间的导航误差统计值具有很好的一致性,北向位置误差RMS分别为8.490,8.526 m,东向位置误差RMS分别为8.660,8.691 m,地向的位置误差RMS分别为5.698,5.971 m;北向速度误差RMS分别为0.260,0.261 m/s,东向速度误差RMS均为0.309 m/s,地向速度误差RMS分别为0.047,0.049 m/s;横滚姿态误差RMS均为0.033°,俯仰姿态误差RMS均为0.039°,航向的姿态误差RMS分别为0.314°,0.316°.因此可以认为方案1与方案2处理精度一致,验证了本文给出的改进Kalman滤波算法对延迟处理的正确性.

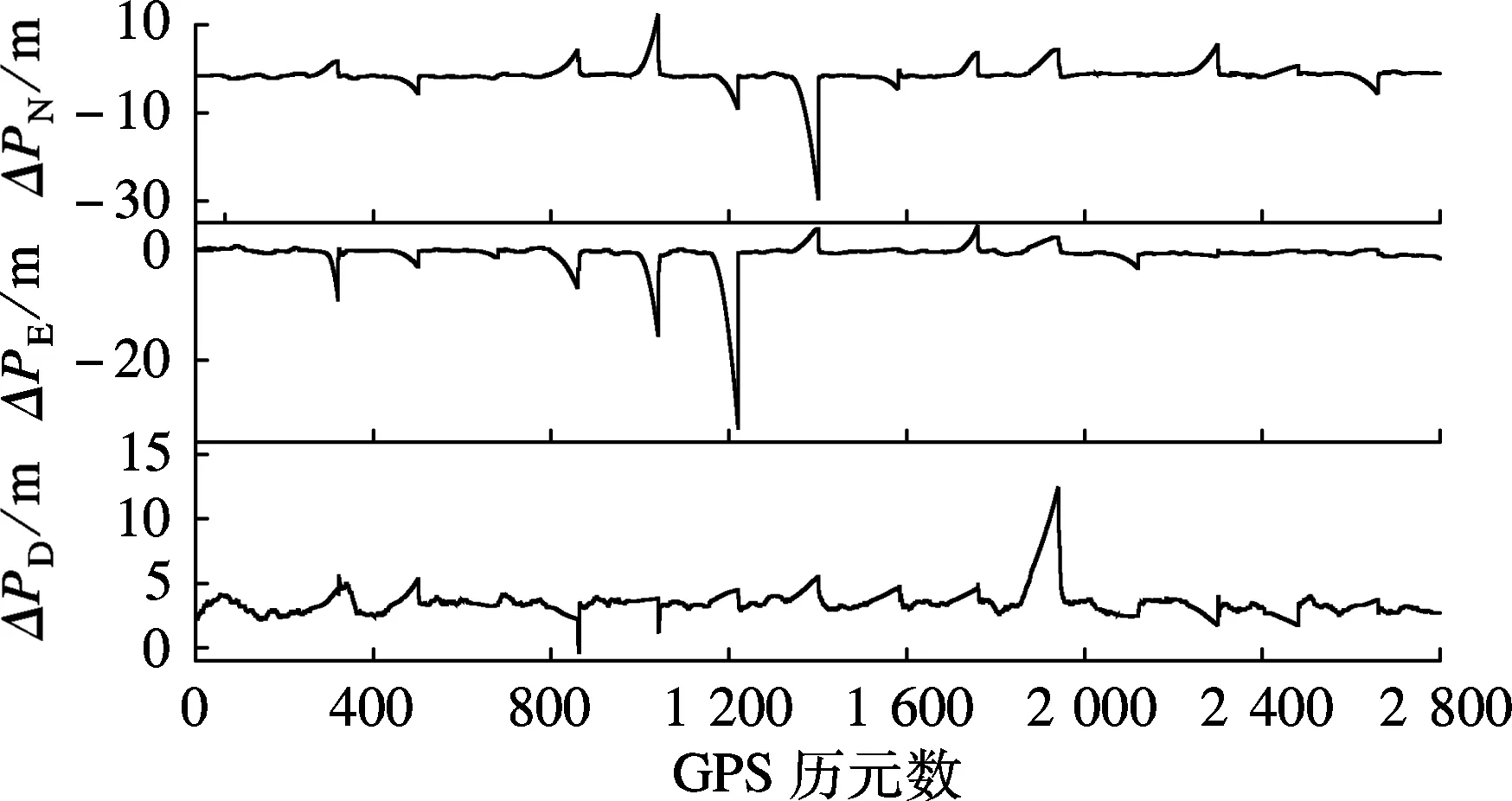
(a) 位置误差

(b) 速度误差

(c) 姿态误差

3.2实时性验证

根据实时记录的计算耗时,绘制出第1次测试的GNSS数据延迟、200 Hz中断计算耗时以及更新计算耗时的频率直方图.从图5可以看出:获取GNSS数据有明显的延迟,大约在56,59以及49 ms,时间延迟的差异可能是观测卫星数目不同以及

(a) 位置误差

(b) 速度误差

(c) 姿态误差

误差项方案1方案2最大值均值RMS最大值均值RMS位置误差/m北向28.7565.7148.49028.7465.8478.526东向31.7365.0488.66031.7305.2068.691地向15.3044.6825.69815.3095.0175.971速度误差/(m·s-1)北向0.8580.1760.2600.8570.1790.261东向0.9610.1810.3090.9610.1840.309地向0.1370.0350.0470.1370.0380.049姿态误差/(°)横滚0.0890.0240.0330.0890.0240.033俯仰0.1050.0310.0390.1040.0300.039航向0.5350.2790.3140.5350.2810.316

导航星历消息数据更新引起的传输数据大小不同所致;200 Hz中断函数的执行时间95%左右的约在0.5 ms,4%左右的约在1.25 ms,少部分约在2.8 ms,没有大于4 ms的部分,因此可以认为中断函数能够在200 Hz中断间隔中执行完毕;组合更新执行时间大部分在45～70 ms,没有大于90 ms的部分.综合图5的统计,可以看出GNSS延迟更新时间大约为150 ms,完全可以在一个GNSS采样间隔内完成组合更新计算.由此看来,本文提出的改进Kalman滤波实时处理方案在实际测试中能够按照设计要求运行,可以满足GNSS/INS实时紧组合系统的实时性要求.

(a) GNSS数据　(b) 200 Hz中断计算

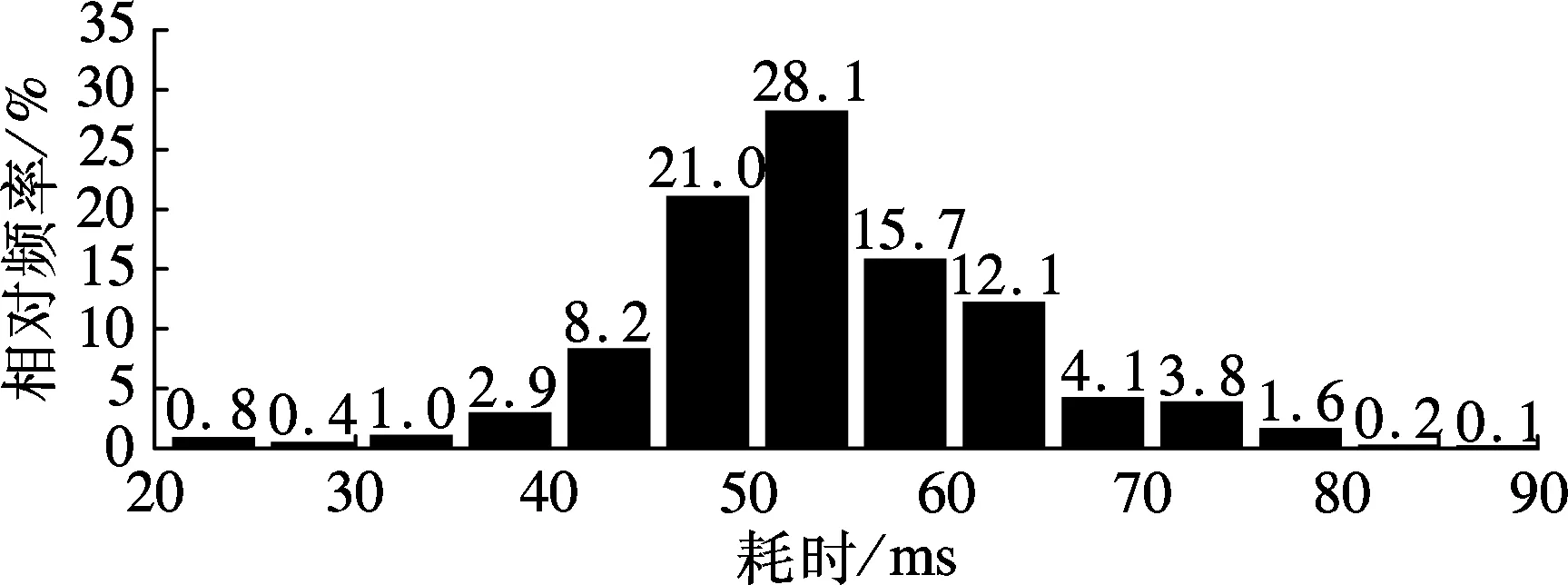
(c) 组合更新计算

从图6可以看出:改进Kalman滤波算法的时间延迟都在5 ms之内,在IMU采样间隔内完成了导航解算,延迟时间大致可以分为2部分：① 延迟较小的部分,完成的是基本机械编排-Kalman预测;② 延迟较大的部分,完成的是要同时处理组合更新量的状态转移以及反馈.标准Kalman滤波算法的时间延迟大部分在100 ms左右,显著大于IMU采样间隔,因而存在严重的时间延迟.相比于标准Kalman滤波计算方式,本文给出的改进Kalman滤波方式有效地减少了时间延迟,确保了实时系统的实时有效性能.

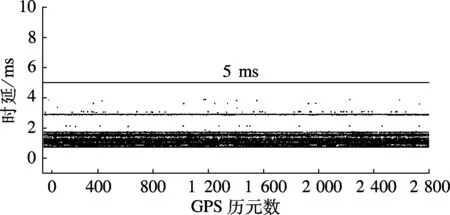
(a) 改进方法

(b) 标准方法

3.3实测精度验证

将第1次测试采集的实时导航结果与参考真值做比较,实时导航误差曲线如图7所示,导航误差统计见表3.从表3的统计结果可以看出,北向、东向、地向的位置误差的标准差分别为0.408,

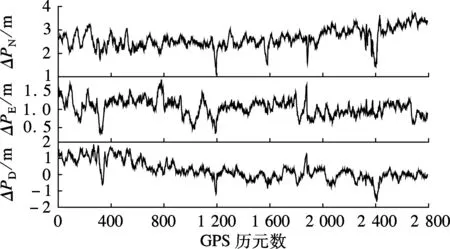
(a) 位置误差

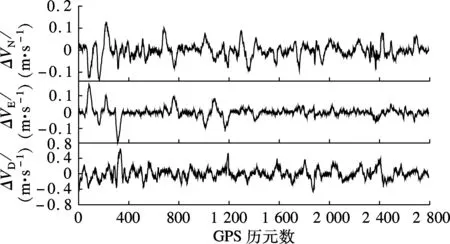
(b) 速度误差

(c) 姿态误差

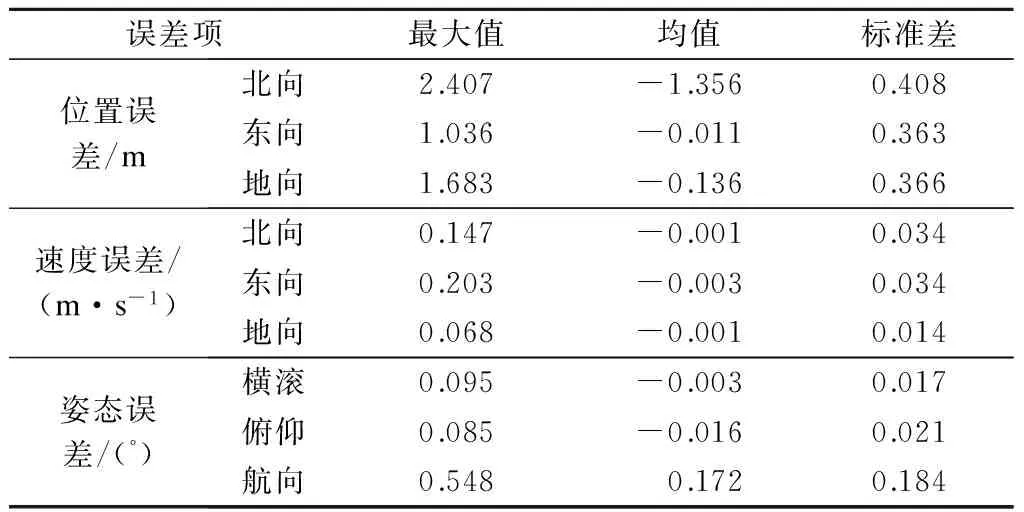
误差项最大值均值标准差位置误差/m北向2.407-1.3560.408东向1.036-0.0110.363地向1.683-0.1360.366速度误差/(m·s-1)北向0.147-0.0010.034东向0.203-0.0030.034地向0.068-0.0010.014姿态误差/(°)横滚0.095-0.0030.017俯仰0.085-0.0160.021航向0.548 0.1720.184

0.363,0.366 m,北向、东向、地向的速度误差的标准差分别为0.034,0.034,0.014 m/s,横滚、俯仰、航向的姿态误差的标准差分别为0.017°,0.021°,0.184°.导航误差均在伪距紧组合理论精度范围内,可以认为运用本文给出的改进Kalman滤波实现的GNSS/INS实时紧组合系统计算精度满足设计要求.

4　结语

本文针对GNSS/INS实时紧组合中存在的GNSS数据获取延迟以及更新计算耗时较长的问题,从Kalman滤波基本原理出发,得到了适用于GNSS观测及更新延迟的Kalman滤波数学模型,并且通过后处理仿真延迟与正常处理做对比,验证了延迟更新处理的正确性.最后,在硬件平台上实现了GNSS/INS实时紧组合系统,实际车载测试表明导航精度及实时性达到了设计要求.

References)

[1]刘川川.基于伪距/多普勒的GPS/INS紧组合算法实现与抗差性能研究[D].武汉:武汉大学卫星导航定位技术研究中心,2012.

[2]王光辉.基于时滞多传感器数据的信息融合滤波[D].哈尔滨:黑龙江大学电子工程学院,2013.

[3]卢晓.观测时滞系统的最优滤波[D].大连:大连理工大学控制理论与控制工程系,2008.

[4]李林林.测量数据延迟下的不完全量测滤波研究[D].南京:南京理工大学控制理论与控制工程系,2012.

[5]Shin Eun-Hwan. Estimation techniques for low-cost inertial navigation[D]. Calgary, Canada: Department of Geomatics Engineering, Calgary University, 2005.

[6]秦永元.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,2000:33-56.

[7]岳俊,何冰.定位坐标分量依赖于卫星高度角的灵敏度分析[J].测绘通报,2014(1):5-8,18. DOI:10.13474/j.cnki.11-2246.2014.0002.

Yue Jun, He Bing. Analysis of the sensitivity-components linked by satellite azimuth in GPS measurement[J].BulletinofSurveyingandMapping, 2014(1): 5-8,18. DOI:10.13474/j.cnki.11-2246.2014.0002. (in Chinese)

[8]孙德波,杨功流,张玉堂.SINS/GPS组合导航序贯滤波算法[J].中国惯性技术学报,2005,13(1):59-63,67. DOI:10.3969/j.issn.1005-6734.2005.01.014.

Sun Debo, Yang Gongliu, Zhang Yutang. Sequential estimation for SINS/GPS integrated navigation [J].JournalofChineseInertialTechnology, 2005, 13(1): 59-63,67. DOI:10.3969/j.issn.1005-6734.2005.01.014.(in Chinese)

[9]刘帅,孙付平,陈坡,等.GPS/INS组合导航系统时间同步方法综述[J].全球定位系统,2012,37(1):53-56.DOI:10.3969/j.issn.1008-9268.2012.01.014.

Liu Shuai,Sun Fuping,Chen Po,et al. A survey of time synchronization solutions in GPS/INS intergrated systems[J].GNSSWordofChina, 2012, 37(1): 53-56. DOI:10.3969/j.issn.1008-9268.2012.01.014. (in Chinese)

[10]Texas Instruments. TMS320C6745/C6747 DSP Technical reference manual[EB/OL]. (2013-03-01)[2014-07-29]. http://www.ti.com/lit/ug/spruh91b/spruh91b.pdf.

[11]Texas Instruments. TMS320C674x DSP CPU and instruction set[EB/OL].(2010-07-10)[2011-08-18]. http://www.ti.com/lit/ug/sprufe8b/sprufe8b.pdf.

[12]Texas Instruments.TMS320C674x DSP megamodule reference guide[EB/OL]. (2010-08-23)[2011-08-16]. http://www.ti.com/lit/ug/sprufk5a/sprufk5a.pdf.

[13]姚章俊,陈蜀宇,卢尧.一种高性能环形缓冲区的研究与实现[J].计算机工程,2012,38(8):228-231. DOI:10.3969/j.issn.1000-3428.2012.08.074.

Yao Zhangjun, Chen Shuyu, Lu Yao. Research and implementation of high-performance ring buffer[J].ComputerEngineering, 2012, 38(8): 228-231. DOI:10.3969/j.issn.1000-3428.2012.08.074. (in Chinese)

Improvement and verification of real-time performance of GNSS/INS tightly coupled integration in embedded platform

Zhang Hongping1Chang Le1Wang Hongchen3Niu Xiaoji1Gao Zhouzheng1,2

(1GNSS Research Center, Wuhan University, Wuhan 430079, China)(2School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China)(3Academy of Science and Technology, Wuhan University, Wuhan 430079, China)

Aiming at the data delay of the global navigation satellite system (GNSS) and too long time consuming problems for Kalman updating existing in the GNSS/INS (inertial navigation system) real time tightly coupled integration system, an improved mathematical model for transferring the error state to the current time in one step after finishing the delayed observation update is proposed based on the Kalman filter theory. In order to verify the effects of the improved model, first, in the Windows platforms, navigation errors during the GNSS signal interruption period of the improved model and the standard Kalman filter model are comparatively analyzed by using the GNSS and the IMU observations of a vehicle testing. The results show that the navigation errors of the two models are similar. So the time delay processing of the improved model is correct. Then, a GNSS/INS real-time tightly coupled integration system based on the digital signal processor (DSP) is developed by using the improved mathematical model and verified by a vehicle testing. The testing results show that compared with the standard Kalman filter model,the improved model can significantly reduce the time delay, thus ensuring the accuracy of the tightly coupled integration system and real-time performance of the system.

GNSS (global navigation satellite system)/INS (inertial navigation system) tightly coupled integration; real-time performance; digital signal processor; Kalman filter

10.3969/j.issn.1001-0505.2016.04.004

2015-11-13.作者简介: 章红平(1977—),男,博士,教授,博士生导师,hpzhang@whu.edu.cn.

国家高技术研究发展计划(863计划)资助项目(2015AA124002)、国家自然科学基金资助项目(41404029).

10.3969/j.issn.1001-0505.2016.04.004.

P228.41

A

1001-0505(2016)04-0695-07

引用本文: 章红平,常乐,汪宏晨,等.GNSS/INS紧组合算法实时性改进与嵌入式验证[J].东南大学学报(自然科学版),2016,46(4):695-701.