利用几何画板软件处理物在水中像的位置*

朱红伟

(宿迁市沭阳如东实验学校　江苏 宿迁　223600)



利用几何画板软件处理物在水中像的位置*

朱红伟

(宿迁市沭阳如东实验学校江苏 宿迁223600)

如何准确处理物在水中像的位置是初中光学知识的难点，常规作图方法较为繁琐．本文将利用几何画板软件，通过构建物像模型经过动态演示后得出像与物的位置关系，并得出相关结论．

几何画板初中物理光的折射虚像

“物在水中像的位置”问题在历年各省市中考卷中时有体现，如何准确判断物像位置是初中光学知识的重难点之一．为此本人查阅了多个文献，发现判断方法各有特点，其中文献[1]先建立折射模型，再通过折射定律及求导公式，得出鱼到水面距离h与像到水面距离h′的关系，并通过类似方法得出侧移d与视角θ的关系，最终得出结论；文献[2]先分析折射特点，并在Excel中进行数据处理，选用4组入射角与折射角数据，后在Word中进行绘图，最终得出鱼在水中像的位置．

笔者认为上述两种方法均存在计算复杂、作图困难、无法动态演示等缺点，结合本人多年使用“几何画板”的经验，认为该软件完全可以通过内置功能准确处理判断鱼像位置，并且可以实现鱼像位置的动态变化，有助于得出科学结论．

“几何画板”是一款美国公司开发后引入中国的教学软件，它具有几何作图、度量测算、参数计算、函数绘图等强大功能，并且课件制作简单，教师只需稍加熟悉就可以制作课件，通过设置函数关系，动态显示物理变量，量化讨论物理过程．本文就以几何画板5.0版为工具，利用其动态显示的特点来构建物像模型，确定物在水中所成像的位置，过程如下.

1　理论推导

现有一光线从水中斜射入空气中(如图1)，令入射角∠SAC、折射角∠GAE分别为α和γ，为方便表达取空气的折射率为1，水的折射率为n(n=1.3)，根据折射定律可知

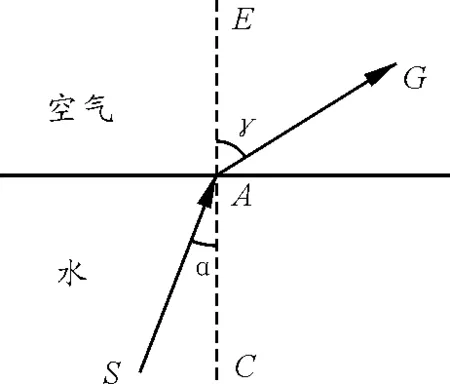
图1　光的折射光路图

讨论：如果已知入射角α，可以求出α的正弦值sinα，那么折射角γ正弦值sinγ=nsinα，因此可以得出折射角γ=arcsin(nsinα)；当求解其他不同介质间的折射时，n值可以变化．

2　课件制作

本文使用软件版本为几何画板5.0版，详细步骤如下：

(1)打开几何画板5.0版，使用线段直尺工具绘制一条水平直线，选中左端点，点击右键选择【属性】→【标签】，设置为M，同理右端点为N，MN即为水与空气的分界面；在MN上任意选取两点，分别标签为A和B，为入射点；

(2)选中A、B两点与线MN，选择菜单【构造】→【垂线】，得到过A，B两点的垂线；选中垂线，选择菜单【显示】→【线型】→【虚线】，这两条线作为法线；

(3)在线MN下方选中一点为物点，标为S；使用自定义工具过S与A，B点作带箭头线段，作为两条入射光线SA，SB；为了便于测量及定义角度，在垂线上各作两点分别位于A点上下方，为C和E，同理B点上下方为D和F(如图2)；

图2　(1)-(3)步最终显示

(4)按顺序选取S，A，C3点，选择菜单【度量】→【角度】，量取∠SAC标签为“入射角αA”；选择菜单【数据】→【计算】，出现“新建计算”界面，选择菜单【函数】→【sin】，再选中“入射角αA”，点击确定，此时显示得入射角的正弦值sin∠SAC，标签为“入射角αA正弦值”(如图3)；相同方法处理光线SB的入射角及正弦值；

图3　窗口“新建计算”界面

(5)选择菜单【数据】→【计算】，出现“新建计算”界面，点击选中“入射角αA正弦值”，在计算界面依次输入“*”、“1.3”，点击确定得到折射角的正弦值“sin∠SAC·1.3”，标签为“折射角γA正弦值”；再次打开“新建计算”界面，选择菜单【函数】→【arcsin】，再选中“折射角γA正弦值”，点击确定，此时显示折射角为“sin-1(sin∠SAC·1.3)”，标签为“折射角γA”；相同方法处理光线SB，得到折射角的正弦值及折射角(以上数据均默认两位小数，如有特殊要求可以选中数值，点击右键打开属性，更改精确度即可)；

(6)双击A点将其作为旋转中心，再选中直线CE，选择菜单【变换】→【旋转】，出现“旋转”界面(图4)，再点击“折射角γA”，点击“旋转”得到一条倾斜直线，将其标签为a；选中直线a，选择菜单【变换】→【反射】，得到直线a相对于直线MN的对称直线，将其标签为b；相同方法处理B点，得到直线c及对称直线d，并将直线a和c隐藏；

图4　窗口“旋转”界面

(7)直线b，d相交于一点为像点，标签为S′；在直线a，c上方分别各选中一点，标签为G和H，G到H即为人的观察范围；使用带箭头线段连接AG与BH，作为两条折射光线；

(8)选中直线b，d将其隐藏，使用线段直尺工具绘制S′到A，B间的线段；选中线段S′A和S′B后更改线型为虚线，这两条线为折射光线的反向延长线；

(9)到此课件制作基本结束，最终效果如图5所示，可以进行一些后期加工，比如通过菜单【显示】调整点与线的类型、颜色等；也可以对无关点C，D，E，F，G，H点进行隐藏，增加课件的简洁度．

图5　最终显示效果图

3　课件演示

在课件中，我们可以通过拉动折射点A，B来调整人的视角，值得注意的是，当人在不同位置时，视角不同，所成像的位置不同，因此本文只选取了3个视角进行分析：

(1)比较图6～8可知，人站在不同位置时，像的位置随视角的变化而变化，但总是在物体的右上方，可总结为像相对于水面变浅，相对于人被拉近；

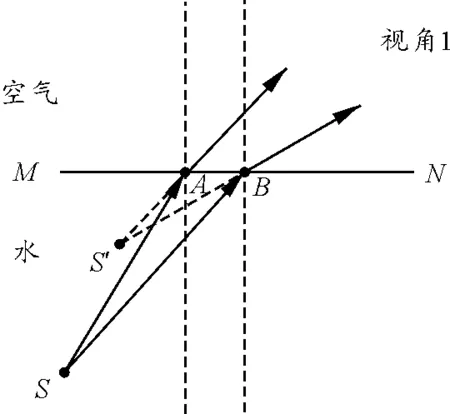
图6　视角1像的位置图

图7　视角2像的位置图

(2)分析图8可知，当人处于物体的正上方时，像也在物体的正上方，但也符合“变浅拉近”规律．

图8　视角3像的位置图

拓展：1)通过课件制作和演示可以发现，当改变入射光线和折射光线方向，就可以模拟演示从水中看岸上景物像的位置变化，由本文可以推导出像变化规律为“变高拉远”；

2)当然也可以通过改变折射率n，演示其他不同介质间物体的成像特点．

4　结语

起初几何画板作为数学工具广为使用，但制作物理课件也同样出色，其课件既可以模拟物理实验又可以进行量化讨论；既是物理实验的延伸，也是定量研究的开始．通过在课件中将物理公式转换为几何函数、将物理图像转换为几何图线、将物理模型转换为数学模型，依托几何画板的众多功能来演示物理实验及解决物理习题．但几何画板也有自身局限性，比如它只能处理具备函数关系的物理知识，无法适用所有物理问题等．同时我们也要清醒地认识到，几何画板只是作为课堂教学的辅助工具，课堂教学还应以学生为主体，不可过分依赖几何画板等信息技术工具而忽略了传统实验等常规教学手段，更应是在传统的教学模式基础上，充分发挥其形象生动、动态变化的特点给课堂增趣、增效，达到培养学生空间想象、科学解题等综合能力的目的．

综上，几何画板功能强大，运用合理可以帮助教师突破教学难点，帮助学生理解学习难点，有助于提高课堂效率．限于个人水平，如有不足之处，请读者批评指正．

1叶玉琴.鱼在哪里.物理教学探讨，2011(9)：62

2王爱红，吴彬彬.用office软件处理鱼在水中像的位置.中学物理，2015(7)：89

2016-04-16)

*系江苏省教育科学“十二五”规划重点课题“大数据视野下通过DIS物理实验激活初中生科学思维的策略与实践研究”，课题编号：E-b/2015/12；宿迁市教育科学“十二五”规划课题，编号：SQ2015GH005；江苏省现代教育技术研究课题“信息技术大环境下苏科版物理实验教学的实践与研究”研究成果之一，编号：40323