C-RAN 中基于Markov模型的小区用户数预测

徐昌彪，朱联军b

（重庆邮电大学 a.光电工程学院； b.通信与信息工程学院，重庆 400065）

C-RAN 中基于Markov模型的小区用户数预测

徐昌彪a，朱联军b

（重庆邮电大学 a.光电工程学院； b.通信与信息工程学院，重庆 400065）

基于排队论和Markov转移模型，对C-RAN（绿色无线接入网）中小区簇所包含所有小区的用户数的变化规律进行预测研究。提出了一种综合考虑历史规律及当前趋势的预测方案，对各小区不同时刻的用户到达率和离开率进行预测。通过求Markov转移模型的瞬态解，得出各小区用户数在不同时刻的统计平均值。在考虑预测误差和系统开销的情况下，求解最优的预测周期。仿真结果表明，较优的预测周期能客观反映实际环境中用户数的变化规律。

绿色无线接入网；马尔科夫转移模型；预测；排队论；最优预测周期；变化规律

0　引 言

通信行业作为全球增长速度最快的行业之一，资源的高效利用已成为关注的焦点。然而现有的资源分配和配置较为低效，虽然在传统的通信网络设计中存在一定冗余，但实际情况并非所有设备都能得到充分的利用。用户移动规律与业务分布的时空变化是影响网络整体通信性能的重要因素。通信中“潮汐效应”［1］会对网络资源造成极大的浪费，其中频谱资源的低效利用最为明显。C-RAN［2］（绿色无线接入网）作为一种较新的网络架构，为各小区协作通信、资源的动态分配提供了条件。在C-RAN中，一个BBU（基带处理单元）通过光纤连接多个RRU（远端射频单元），一个RRU对应一个小区，BBU可对各个RRU进行集中管理与调度，并依据历史数据来预测未来的负载，以对资源进行预分配，CRAN特有的架构体系为本文的研究奠定了基础。为了提高频谱资源利用率，建立一个能反映客观现实的用户移动规律的模型，预测未来各小区人数的变化规律具有重要的现实意义。

1　研究现状

当前，对用户移动模型的研究报道较多。在异构网络中，文献［3］创建了一种基于二维终端速率分类与状态转换的移动模型，并且给出了相应的Markov分析方法。文献［4］运用排队论对游客在公园中因旅游景点的影响而移动进行了研究。文献［5］提出了RRM（无线资源管理）移动模型在WNAN（无线体域网）中的应用，以捕获体域网用户在建筑物间移动时的动态特征。基于统计数据对用户在微蜂窝小区内的驻留时间进行分析，文献［6］得到其概率分布与Pareto分布非常接近。文献［7］提出了一种移动话务的潮汐效应智能化解决方案及基带池资源技术，以提高基站的利用率，降低建网成本和能耗。文献［8］提出一种优先路径室内移动模型，运用Markov模型和最短路径算法对其进行求解。文献［9］基于真实的建筑环境数据，提出了一种复杂三维室内用户移动模型。文献［10］依据C-RAN中的负载需求，采取BBU集中对RRU进行资源分配，资源利用率提高了70%。根据负载的变化规律，文献［11］通过拟合法，将资源的需求拟合成与时间的变化关系，并对其进行资源分配，但没有对引起负载变化的根本原因（用户的有规律移动）进行研究。由现状可知，对C-RAN架构下小区用户数变化的模型研究较少，且很多对用户数的预测研究都是基于当前的趋势进行的，忽略了历史规律这一重要参考依据。

2　基于Markov的小区用户数量变化模型

2.1小区簇的选取

为了简化系统的网络架构和调度过程的复杂度，协作式处理和调度机制应限制在几个小区组成的“小区簇”内进行。小区簇的选取应满足稳定性、相邻性和起伏性的特征。稳定性指用户数量的稳定，是本文研究的前提条件，只有在相对稳定的环境下，即用户数量维持在比较稳定的状态下，后续的资源分配才具有意义。在小区簇中，虽然各个小区用户数均存在峰值，但其时间不一样，相互间具有互补性。假设小区簇内有n个小区，小区m在t时刻的用户数用cellm（t）表示，ALL表示小区簇的总用户数，则小区簇内小区在任意时刻的用户数满足

相邻性是指各个小区物理位置彼此相邻，小区簇内所有小区的RRU数据均通过光纤传输到BBU进行处理，且RRU为分布式部署，BBU部署在小区簇的中心位置。在一个大的范围内，用户数量一般较为稳定，小区簇内所有小区彼此相邻。

起伏性是指单个小区用户数量随时间不断变化。正是由于用户数量的不断变化，才导致通信潮汐效应的存在。

2.2移动模型的建立

在研究小区用户数量变化时，只考虑移动用户在小区簇内流动。因此，cellm（小区m）增加的用户只考虑来自小区簇内的其他小区；同样，减少的用户只考虑流入到小区簇内的其他小区。图1所示为cellm内用户的实际转移模型。

求解上述模型的转移概率较为困难，但本文所研究的用户变化是在一个小区簇中进行，因此可对模型进行简化。将到达率λ和离开率μ看作是各个小区流入到本小区的到达率和从本小区离开到各个小区离开率的累加值，简化移动模型如图2所示。

图1　小区用户转移模型

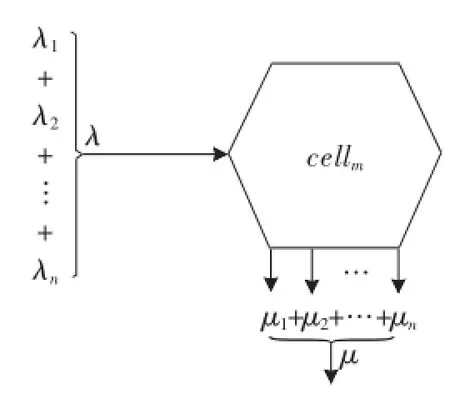
图2　简化移动模型

2.3简化移动模型的Markov分析

以单个小区作为研究对象。假设用户到达和离开小区的时间间隔均服从指数分布，且在同一时刻不可能有两个用户离开，等效于排队模型中有1个服务窗口。本文最佳预测周期作为一个计算周期，以分钟为周期的最小单位，计算不同时刻的用户数，在每次计算时都认为λ和μ是一个定值。为了求出用户数量的变化情况，需要计算出用户的暂态解。模型的用户数量变化满足M|M|1排队模型，其Markov转移过程如图3所示，图中N表示小区中的最大用户数。

图3　用户数变化的Markov转移模型

此建模的目的是通过模型来计算潜在用户数，即通过用户到达小区和离开小区前一时刻的规律和历史同一时间段的规律来预测下一时刻小区用户的数量。假设0时刻系统有i个顾客，在t时刻系统有k个顾客的概率为pik（t），则系统的暂态方程为

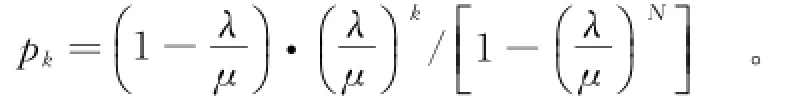
结合实际环境，由于单个小区的最大用户数一般较大，在求解时可近似将上述等式的分母看为1，因此稳态解为

式（2）为线性差微分方程，由于小区用户数的最大容纳值较大，因此其暂态解近似为

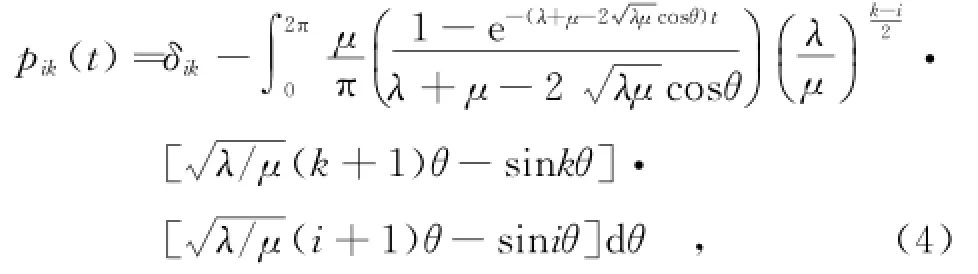
式中，δik为单位序列。当ρ＞1时，瞬态解无法得到相应的理论公式，在仿真时可以运用MATLAB中求解差微分方程的函数进行求解。

2.4λ和μ的求解

小区用户到达率λ和离开率μ的确定是相对关键的部分。在求解λ和μ时，结合单方法预测和组合预测的优点，既考虑历史规律，又考虑当前规律的基础上，提出了一种新的预测方法：基于历史-当前的二次幂递增预测方法，权值因子按两倍关系变化，相隔时间越久，其权值越小，对当前求解值的影响越小。在一个预测周期T内λ和μ是一个定值，假设小区m第x天a到b时段的到达率为λ，且只考虑当前求解时刻的前一周期和前n天的情况，则可以表示为

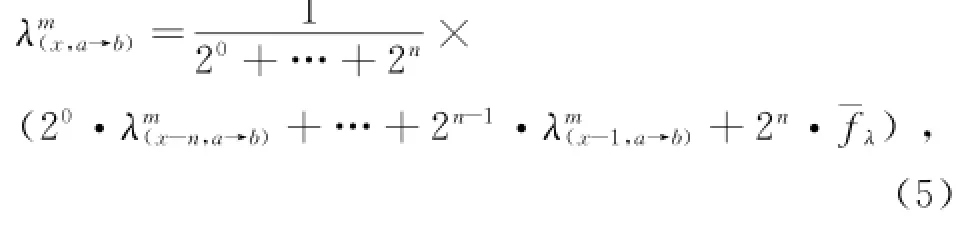
式中，¯fλ为统计平均值，通过小区m第x天前一周期的数据来进行求解，即通过小区m第k天时刻a-T到时刻b-T的数据来求解。计算方法为：a-T 到b-T时间段内各个时刻的到达率已知，以1 min为间隔统计到达小区的人数，假设数据分别为，使用二次拟合曲线，用最小二乘法求解λ关于时间的函数，可表示为

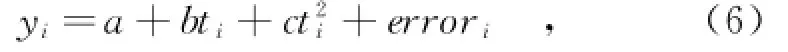
式中，errori为误差项；a、b、c为拟合常数。使用二次拟合是因为在较小的时间间隔内，用户数量的变化趋势几乎满足二次曲线规律。a、b和c满足如下方程：

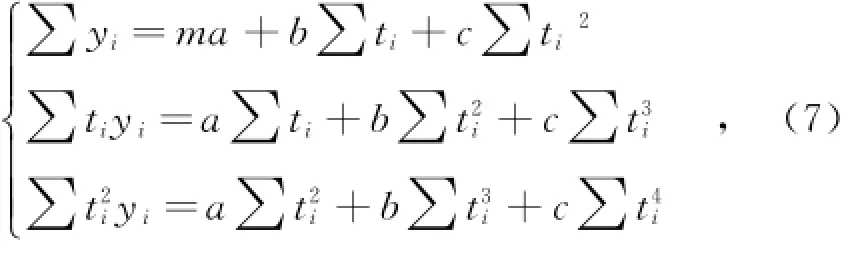
将求得的系数代入式（6），以t为变量，即可求出不同时刻的y值。定义¯fλ的值为

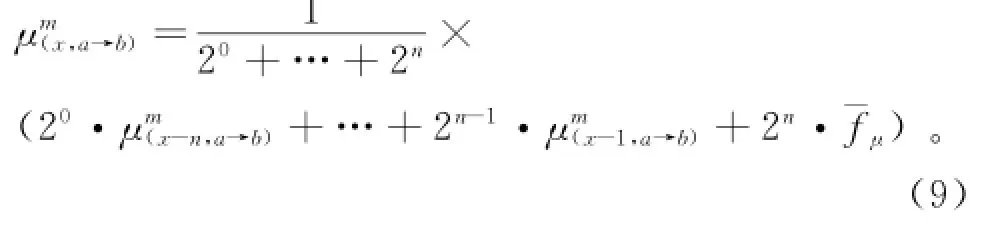
2.5不同时刻用户数量的求解

对于小区m，假设当前的人数为i，最大容纳人数为Max um，小区t时刻的人数为user（t），根据式（4）、（5）和（9），user（t）可表示为

3　仿真验证

采用MATLAB和Microsoft Visual Studio 2005仿真软件进行仿真，为了体现环境中小区用户的流动性，选取较为典型的区域作为仿真研究区域，仿真场景如图4所示。

图4　仿真场景

在求解结果时，n值取为3，即只考虑前3天的历史情况，并将日期分为工作日和节假日，用同类日期的历史数据来计算λ和μ。在求解最佳预测周期时主要考虑系统的开销over（T）和预测误差dev（T），定义预测效益函数为Be（T），表示为

式中，α+β=1，Be（T）越小越好。如要重点考虑系统开销，则使α＞β；如要重点考虑预测误差，则使α＜β。dev（T）的求解如下：假设预测周期为T，将一天内每一分钟的预测值与实际值的方差求和，对不同周期的dev（T）做归一化处理。设小区m在t时刻的预测人数和实际人数分别为user pmre（t）和useramct（t），则小区m的预测累加方差Δm（T）可以表示为

不同周期（周期范围为1～60 min）的dev（T）为其归一化方差，则小区m的devm（T）可以表示为

仿真选择5个小区，dev（T）为5个小区的平均加权值。在考虑开销时，由于空间复杂度几乎相同，因此主要考虑时间复杂度。当T较小时，系统需要不断地计算λ和μ等，占用时间几乎与T成反比。因此over（T）可以表示为

在求解Be（T）时重点考虑系统开销，取α=0.6、β= 0.4。预测误差、系统开销与T的关系如图5所示。

图5 预测误差、系统开销与T的关系

图5中，系统开销和预测误差均为归一化值，系统开销随T的增大而减小。预测误差呈现两边大中间小的趋势，最佳预测周期为10 min左右。当T＜10时，误差随T增加而减小，这是由于突发性会导致预测偏差较大；当T＞10时，滞后性会使误差随T增大而增大。

Be（T）与T的关系如图6所示。由图可知，当α =0.6、β=0.4时，系统的最佳预测周期约为17 min。将本文所提预测方案与AR（自回归）预测方案进行对比，对两个预测方案不同的时段（以1 h为单位，求出每1 min的平均方差）误差的归一化值进行分析，图7所示为两种方案的对比图。由图可知，本文所提预测方案较AR预测在一定程度上提高了λ和μ的预测准确性，进而提高了小区人数预测的准确性，在人数急剧变化的时间段最为明显，如7∶00～8∶00之间。当用户流动较缓慢时，预测误差较小，如夜间时段。

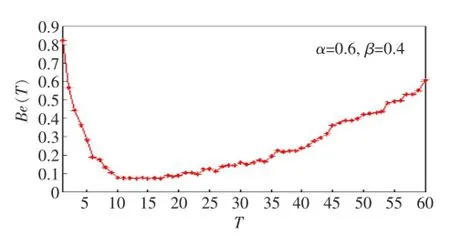
图6　Be（T）与T的关系

图7　方案对比

4　结束语

对整个小区簇内所有小区的用户移动进行研究，建立了用户转移模型，根据历史数据对小区未来的用户数量进行预测。在预测过程中重点求解最佳预测周期，由最佳周期预测小区簇中各个小区未来的用户数变化情况。预测时不仅考虑了历史规律，更着重考虑了用户数量当前的变化趋势，并与AR预测进行对比。本文的研究结论为资源分配提供了理论支撑，资源分配也将是本课题的后续方向。

［1］ 杨璘.绿色无线接入网架构C-RAN研究［D］.北京：北京邮电大学，2011.

［2］ 黄宇红.C-RAN无线接入网绿色演进白皮书［D］.北京：中国移动通信研究院，2010.

［3］ 刘琪，袁坚，山秀明，等.3G/WLAN网络中基于终端移动与业务认知的动态负载均衡机制［J］.计算机学报，2010，（9）：1569-1579.

［4］ Solmaz G，Akbas M，Turgut D.A Mobility Model of Theme Park Visitors［J］.IEEE Transactions on Mobile Computing，2015，14（12）：2406-2418.

［5］ Misra S，Mahapatro J，Mahadevappa M，et al.Random room mobility model and extra-wireless body area network communication in hospital buildings［J］.IET Networks，2014，4（1）：54-64.

［6］ Thajchayapong S，Peha J M.Mobility patterns in microcellular wireless networks［J］.Mobile Computing，IEEE Transactions on，2006，5（1）：52-63.

［7］ 赵亚玲.一种移动话务的潮汐效应解决方案［J］.科技视界，2014，（30）：238-238.

［8］ Ning L，Wang Z，Guo Q.Preferred Route Indoor Mobility Model for Heterogeneous Networks［J］. Communications Letters，IEEE，2014，18（5）：821-824.

［9］ Rose D M，Jansen T，Hahn S，et al.Impact of realistic indoor mobility modelling in the context of propagation modelling on the user and network experience ［C］//EuCAP 2013.Gothenburg，Sweden：IEEE，2013：3979-3983.

［10］Khan M，Alhumaima R S，Al-Raweshidy H S.Reducing energy consumption by dynamic resource allocation in C-RAN［C］//EuCNC 2015.Paris，France：IEEE，2015：169-174.

［11］赵岩琨.LTE系统自优化节能技术研究［D］.北京：北京邮电大学，2012.

Research on the Prediction of the Number of Cell Users Based on Markov Model in C-RAN Network

XU Chang-biaoa，ZHU Lian-junb
（a.School of Optoelectronic Engineering； b.School of Communication and Information Engineering，Chongqing University of Posts and Telecommunications，Chongqing 400065，China）

In this paper，the variation of the number of cell's users within the cluster is studied based on Queuing theory and Markov transition model in C-RAN network.We proposes a prediction scheme to calculate the cell's arriving rate and leaving rate by considering the history regular and the current trend.By solving the transient solution of the Markov transition model，the statistical average of the every cell's users is achieved at different times.Considering the prediction error and the system overhead，the optimal period of the prediction is obtained.The simulation result shows that better prediction period can accurately reflect the variation of the users in the realistic environment.

C-RAN；Markov transition model；predict；queuing theory；the optical prediction period；variation

TN926

A

1005-8788（2016）04-0067-05

10.13756/j.gtxyj.2016.04.020

2016-04-15

国家自然科学基金资助项目（61301124）

徐昌彪（1972-），男，重庆人。教授，工学博士，主要从事未来网络方向的研究。

朱联军，硕士研究生。E-mail：18523854021@163.com