气象因素对沥青路面内部温度的影响及定量分析
谭志远, 李 强,2, 肖标丁
(1.长沙理工大学, 湖南 长沙 410004; 2.道路结构与材料交通行业重点实验室, 湖南 长沙 410004; 3.云南大学 城市建筑与规划学院, 云南 昆明 650091)
气象因素对沥青路面内部温度的影响及定量分析
谭志远1, 李强1,2, 肖标丁3
(1.长沙理工大学, 湖南 长沙410004;2.道路结构与材料交通行业重点实验室, 湖南 长沙410004;3.云南大学 城市建筑与规划学院, 云南 昆明650091)
根据在沥青路面现场试验段获得的路面温度与气象数据,利用聚类分析和逐步回归的方法优选出可以表征路面内部温度变化规律的基本指标,建立沥青路面内部温度与基本指标的多元回归式。预测值与实测值对比分析表明回归公式具有很高的精度,可用于沥青路面内部温度预测。
沥青路面; 内部温度; 气象数据; 聚类分析; 逐步回归
0 前言
我国公路事业发展至今,沥青路面因行车舒适、易于修补和噪音低等特点得到了广泛的应用。但沥青作为典型的温度敏感性材料,其路用性能与力学特性随温度变化而变化,如夏季易出现车辙、推挤等病害,冬季低温时易产生收缩裂缝。此外,沥青路面暴露在野外自然环境中,其内部温度受当地气候(如环境温度、环境湿度、太阳辐射、降雨、风速等)与水文条件的影响。因此,研究各气象因素对路面内部温度的影响具有重要意义。
影响路面温度的因素分为外因与内因两部分:外因主要是气象因素,内因则是指路面材料特性和结构组成等[1]。过去几十年,人们研究路面温度场的方法有理论法和统计分析法。早在20世纪中叶,Barber就用热传导方程计算路面的最高温度[2]。我国严作人[3]、吴赣昌[4]和徐世法[5]、孙立军[6]等学者在理论分析和预测建模也做了大量的研究,并得到不同的路面温度场模型。统计法因模型简单实用、参数便于获取等优点得到了很大的应用[7]。美国SHRP将沥青路面内部20 mm处的温度定义为沥青路面最高温度[8]。本文利用建立小型气象站和在沥青路面内部埋设温度传感器进行监测的方法,在获取大量监测数据的基础上,剔除部分不合理和关联不大的数据,并考虑了部分气象因素对路面温度的累积性和非线性等特点,采用SPSS软件对众多气象参数进行分类和筛选,利用逐步回归方法建立沥青路面内部温度与气象指标的关系。
1 现场监测数据分析与处理
1.1气象因素对路面温度的影响
沥青路面现场试验段监测数据包括:环境温度T、露点Td、环境湿度Ha、雨量R、风速S、太阳辐射瞬时值I、太阳辐射0.5 h累积值Q以及沥青路面内部20 mm深度处的温度T20(取两检测点的均值)。图1为浙江省温州市G104(京福线)永嘉县境内K1869+000的瓯北公路管理站监测点典型的沥青路面内部温度T20与环境温度T、太阳辐射累积值(0.5 h)1 d内的变化曲线。
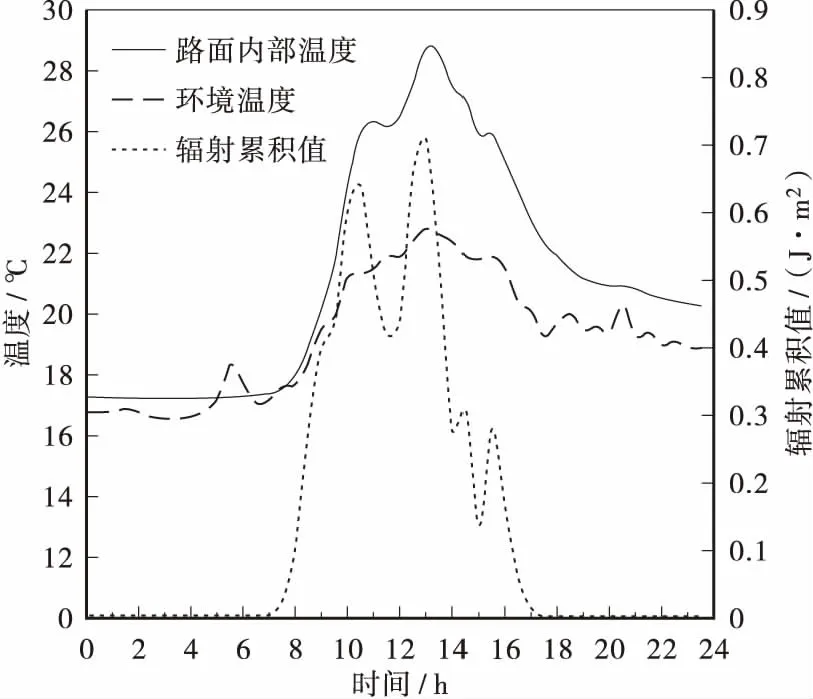
图1 路面内部温度、环境温度和辐射累积值(0.5 h)的变化曲线(温州永嘉瓯北站,2015年11月13日) Figure 1 The change curve of road internal temperature,environment temperature and the cumulative value(0.5 h) of radiation(yongjia station in wenzhou,on Nov 13,2015)
从图中可以看出:沥青路面温度随环境温度和太阳辐射累积值的变化而变化,变化趋势具有一致性,但路面内部温度峰值滞后于环境温度峰值和太阳辐射累积值峰值,也就是环境温度和太阳辐射对沥青路面内部温度T20的影响具有滞后性和累积性的特点,但滞后时间不相同,太阳辐射累积值比环境温度的影响更滞后。
1.2现场监测数据处理
由于现场沥青路面内部埋设的两个温度传感器环境条件基本一致,其观测值应该一致,两者读数互为校核与备份。但由于传感器误差、埋设操作、行车荷载等因素影响,其读数会存在一定的差异。因此,必须通过数据统计分析,剔除不合理的数据,然后取两个路面温度读数的均值作为路面结构内部温度,保证监测数据有效性和可信度。
经过对现场实测数据进行统计分析,两个路面温度传感器实测温度差值符合正态分布,为了保证实测数据置信概率大于95%,剔除两个路面内部温度实测值之差的绝对值≥0.9 ℃的观测数据后,取两测点温度的平均值作为路面内部温度观测值。
一般来说,环境与路面间的温差和风速是影响路面和大气产生热传导和热对流的主要因素,太阳辐射强度、降雨量和环境湿度是影响路面吸收太阳辐射的主要因素。因此,路面温度场的环境影响因素有环境温度、太阳辐射、风速、降雨量、湿度等,但这些环境因素对路面内部温度的影响程度是不一样的。
2 气象因素指标的筛选
上述27个气象参数都有特殊意义,且26个自变量间存在相关性,但由于数据量大且指标数量多,采用26个自变量表征路面温度T20显得非常繁琐。因此,有必要通过分析筛选出基本的气象指标进行表征和分析。
常用的选取基本指标的方法有逐步回归、主成分分析、聚类逐步回归等方法[9]。用逐步回归方法解决多变量问题时,可能会剔除一些显著因子,从而降低数据处理的准确性[10];而主成分分析不能简化变量,只是利用原指标重构后呈不相关的新指标代替原指标,显然不适用于本分析[11];聚类逐步回归法克服了前二者的不足,它能够简化指标同时避免了显著因子被剔除。因此,本文使用聚类分析对26个自变量参数进行分类,再采用逐步回归对各个类别逐步筛选,得出每组类别中效应最显著的指标,从而得到表征路面温度变化的基本指标。
2.1聚类分析
聚类分析可以有效研究事物间的亲疏关系,它包括模糊聚类、动态聚类、系统聚类等,考虑到模糊聚类原理复杂,实际推广较难;动态聚类受经验影响明显,容易被个别数据干扰[12];系统聚类不受经验影响且计算效率较高,具有较高的实用价值[13]。
首先采用5种系统聚类法(最近邻元素法、质心聚类法、组间联接法、组内联接法和中位数聚类法)对上述26个自变量参数进行分类。数据分类结果如下:

Ⅱ类:I、Q0.5、Q1、Q1.5、Q2、Q2.5、Q3、Q3.5、Q4、Q4.5、Q5、Q5.5
Ⅲ类:Ha、R。
但露点Td和风速S具体属于哪种类别,需要进一步分析。本文采用偏相关分析法判别露点Td和风速S与其他参数间的亲疏关系,以确定二者的最终类别。
2.2偏相关分析
先按式(1)求出各参数间的Pearson相关系数,按式(2)求出偏相关系数,去除其余参数的影响。
(1)
(2)
式中:r为变量的相关系数;n为变量数;rpq(k)为控制变量k时,p与q的偏相关系数;rpk为变量p和k的相关系数。
将27个气象参数进行式(1)、式(2)的计算,列举其中一部分参数的偏相关系数见表1。

表1 气象参数偏相关分析Table1 Partialcorrelationanalysisofmeteorologicalparameters参数T20TT0.5T2T2T20.5T22TdHaSIQ0.5Q3.5T201 0.8820.8810.8660.9010.8990.8830.5920.0260.1110.5020.5610.709T0.88210.9990.9910.9860.9850.9770.8710.406-0.0350.2310.2560.383T0.50.8810.99910.9950.9840.9860.9810.8720.409-0.0390.2100.2370.376T20.8660.9910.99510.9760.9800.9860.8740.422-0.0470.1490.1760.342T20.9010.9860.9840.97610.9990.9890.8230.334-0.0070.2760.3060.442T20.50.8990.9850.9860.9800.99910.9940.8250.337-0.0100.2520.2840.435T220.8830.9770.9810.9860.9890.99410.8270.351-0.0170.1850.2160.398Td0.5920.8710.8720.8740.8230.8250.82710.797-0.209-0.024-0.0260.066Ha0.0260.4060.4090.4220.3340.3370.3510.7971-0.341-0.316-0.351-0.343S0.111-0.035-0.039-0.047-0.007-0.010-0.017-0.209-0.34110.2540.2690.244I0.5020.2310.2100.1490.2760.2520.185-0.024-0.3160.25410.9200.741Q0.50.5610.2560.2370.1760.3060.2840.216-0.026-0.3510.2690.92010.824Q3.50.7090.3830.3760.3420.4420.4350.3980.066-0.3430.2440.7410.8241
从表1可以看出:参数间的亲疏关系。露点Td与Ⅰ类参数的偏相关系数都在0.823以上,大于露点Td与Ⅱ类参数的偏相关系数,说明可以将露点归为Ⅰ类;风速S与Ⅰ类、Ⅱ类参数的偏相关系数都较低,因而将风速S归为Ⅲ类,得到的最终的分类见表2。

表2 参数分类结果Table2 Classificationresultsoftheparameters类别气象参数ⅠT、T0.5、T1、T1.5、T2、T2、T20.5、T21、T21.5、T22、TdⅡI、Q0.5、Q1、Q1.5、Q2、Q2.5、Q3、Q3.5、Q4、Q4.5、Q5、Q5.5ⅢHa、R、S
根据系统聚类和偏相关分析可以看出哪几种参数属同类,但无法获得其中哪个参数的效应最显著,得不到最佳组合,所以需要用逐步回归法得到最佳参数组合。
2.3逐步回归
本分析中因变量为路面温度T20,其余气象参数为自变量。利用逐步回归筛选并剔除引起多重共线性的变量,其具体步骤见图2。经过逐步回归,使得最后保留在模型中的解释变量既是重要的,又没有严重多重共线性[14]。
利用SPSS软件的逐步回归分析对26个自变量进行方差贡献排序和检验,将排在前8位的变量逐步回归判别结果见表3。
入选的8个参数中,T2、T2和Td同属于Ⅰ类参数,因此剔除方差贡献最小的Td;Q3.5、Q1和Q5.5同属于Ⅱ类参数,选择方差贡献最大的Q3.5;同理在Ⅲ类参数中选中Ha,故得到表征路面温度规律的4个基本参数:环境温度二次幂T2、前2 h平均环境温度T2、前3.5 h平均太阳辐射累积值Q3.5、环境湿度Ha。
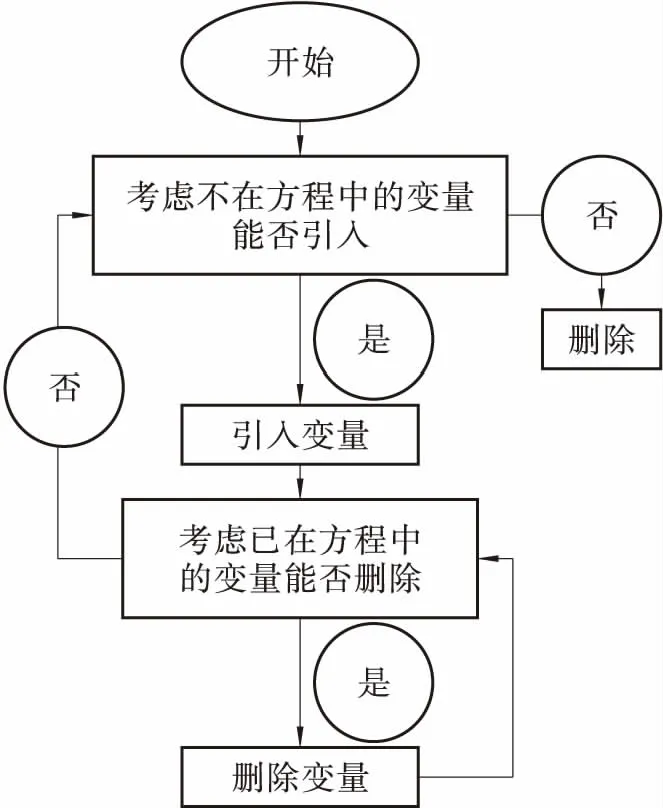
图2 多元逐步回归分析的基本步骤Figure 2 Basic program of the multivariate stepwise regression method
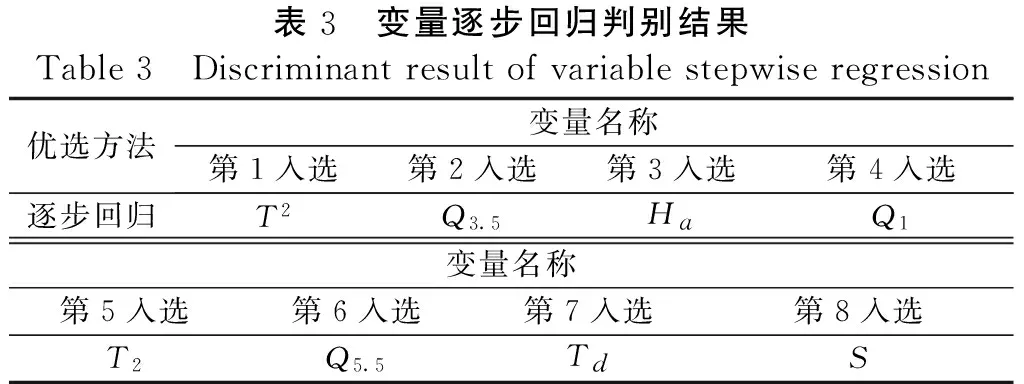
表3 变量逐步回归判别结果Table3 Discriminantresultofvariablestepwiseregression优选方法变量名称第1入选第2入选第3入选第4入选逐步回归T2Q3.5HaQ1变量名称第5入选第6入选第7入选第8入选T2Q5.5TdS
3 气象指标与路面内部温度关系拟合分析
由环境温度二次幂T2、前2 h内平均气温T2、前3.5 h平均太阳辐射累积值Q3.5、环境湿度Ha表征路面内部温度T20可有多种函数表达形式。偏最小二乘回归可以高效解决回归方程中变量间的多重共线性问题,有些类似于主成分分析与典型相关分析的结合,且效果较好。
在SPSS软件中实现多元回归分析时,采用的就是偏最小二乘回归法,其步骤为选路面温度T20为因变量,选择T2、T2、Q3.5、和Ha为自变量,并在回归方法中选择“逐步”,可以得到回归式的回归系数、回归系数的平方、校正回归系数的平方以及回归式的相关系数等,如表4和表5所示。
由以上步骤以及表4、表5可以得出回归式如式(3)所示,回归相关系数R2为0.965。
T20=7.793+0.002T2+9.051Q3.5-0.06Ha+0.892T2
(3)
式中:T20为距路表20 mm深度处的温度,℃;T为当前环境温度,℃;Q3.5为前3.5 h平均太阳辐射累积值,J/m2;Ha为环境湿度,%;T2为前2 h环境温度的平均值,℃。

表4 模型综述表Table4 Modeloverviewtable步骤相关系数RR2R2校正值标准误差估计值变化统计量R2变化值F值df1df2Sig.FChange10.9010.8120.8111.8600.8126534.327115170.00020.9650.9310.9311.1250.1202630.475115160.00030.9710.9440.9431.0180.012335.724115150.00040.9820.9650.9650.8040.021916.853115140.000 注:此逐步回归共四个步骤,每个步骤中被解释变量都是路面温度T20,步骤1中引入的解释变量为环境温度的二次幂T2,步骤2、3、4中依次引入的解释变量为前3.5h平均太阳辐射累积值Q3.5、环境湿度Ha、前2h内平均环境温度T2;F值表示回归分析中的检验统计量,sig.FChange表示显著水平。
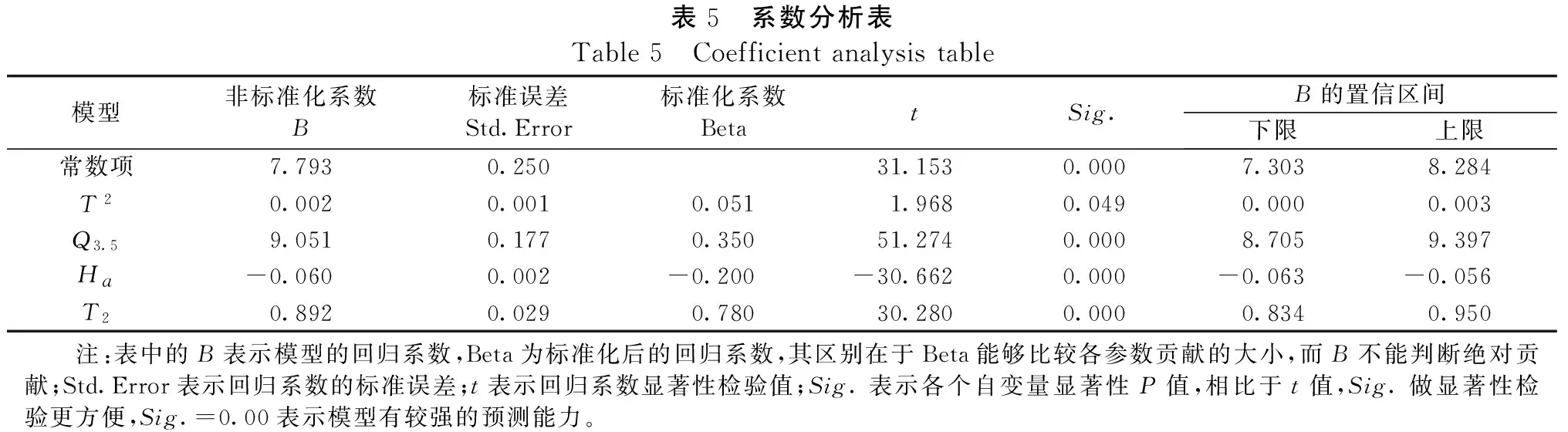
表5 系数分析表Table5 Coefficientanalysistable模型非标准化系数B标准误差Std.Error标准化系数BetatSig.B的置信区间下限上限常数项7.7930.25031.1530.0007.3038.284T20.0020.0010.0511.9680.0490.0000.003Q3.59.0510.1770.35051.2740.0008.7059.397Ha-0.0600.002-0.200-30.6620.000-0.063-0.056T20.8920.0290.78030.2800.0000.8340.950 注:表中的B表示模型的回归系数,Beta为标准化后的回归系数,其区别在于Beta能够比较各参数贡献的大小,而B不能判断绝对贡献;Std.Error表示回归系数的标准误差;t表示回归系数显著性检验值;Sig.表示各个自变量显著性P值,相比于t值,Sig.做显著性检验更方便,Sig.=0.00表示模型有较强的预测能力。
为验证回归式(3)的可靠性,利用式(3)得到的2015年11月13日路面温度预测值T20′与现场沥青路面内部温度实测值T20进行对比如图3所示。
从图3可以看出:预测值与实测值偏差比较小,说明路面温度的预测结果比较可靠。因此,运用本文的方法筛选出来的基本指标合理,建立的回归公

图3 沥青路面温度预测值T20′与实测值T20对比Figure 3 Comparison of asphalt pavement temperature predictive values with actually measured values
式能够准确地表征路面温度的变化规律。
4 结语
① 采用系统聚类分析和逐步回归的方法从气象参数中选出了4个指标,即环境温度二次幂T2、前2 h内平均气温T2、前3.5 h平均太阳辐射累积值Q3.5和环境湿度Ha。分析表明这4个基本气象指标可以全面反映沥青路面深度20 mm处的温度T20变化规律,为沥青路面温度场的研究提供参考。
② 采用偏最小二乘回归法获得的沥青路面内部温度T20与4个基本气象参数间的关系式可准确预估沥青路面内部温度,为沥青路面的结合料选择和老化分析提供依据。
③ 沥青路面内部温度场不仅与气象因素有关,还与路面的结构组成、材料组成等有关,故本文拟合公式的适用性有待进一步验证。
[1]唐娟.海南省气候区划和温度场与沥青路面车辙相关性研究[D].长沙:中南大学,2012.
[2]Barber,E.S.Calculation of Maximum Pavement Temperature from Weather Reports[R]//Highway Research Board,Bulletin 168.Washington D.C.:National Research Council,1957:51-53.
[3]白青波,李旭,田亚护.路基温度场长期模拟中的地表热边界条件研究[J].岩土工程学报,2015,37(6):1142-1149.
[4]张乃计,梁乃兴,朱亚平.影响沥青路面温度场的气象要素分析[J].重庆交通大学学报:自然科学版,2011,30(6):1327-1330.
[5]马正军,谈至明,钱晨.沥青路面面层温度分布规律[J].中国公路学报,2014,27(4):9-15.
[6]孙立军,秦健.沥青路面温度场的预估模型[J].同济大学学报:自然科学版,2006,34(4):480-483.
[7]胡滨,赵毅,张保立.沥青路面温度模型及分析方法比较[J].交通科技与经济,2009(03):46-48.
[8]黄冰,颜可珍,林峰.沥青低温性能评价指标的灰色关联度分析[J].公路工程,2010,35(02):19-22.
[9]韦秉旭,刘斌,刘雄.膨胀土裂隙定量化基本指标研究[J].水文地质工程地质,2015,42(5):84-89.
[10]王志强,柴寿喜,仲晓梅,等.多元逐步回归分析应用于固化土强度与微结构参数相关性评价[J].岩土力学,2007,28(08):1650-1654.
[11]林海明,杜子芳.主成分分析综合评价应该注意的问题[J].统计研究,2013(08):25-31.
[12]范雷,王亮清.唐辉明.节理岩体结构面产状的动态聚类分析[J].岩土力学,2007,28(11):2405-2408.
[13]胡雷芳.五种常用系统聚类分析方法及其比较[J].浙江统计,2007(04):11-13.
[14]盛增荣.城市房地产投资环境评价及实证研究[D].重庆:重庆大学,2006.
The Effect of Meteorological Factors on Asphalt Pavement Internal Temperature and Quantitative Analysis
TAN Zhiyuan1, LI Qiang1,2, XIAO Biaoding3
(1.School of Traffic and Transportation Engineering, Changsha University of Science & Technology, Changsha, Hunan 410004, China;2.Key Laboratory of Road Structure & Material of Ministry of Communications, Changsha, Hunan 410004, China;3.School of City Building and Planning, University of Yunnan, Kunming, Yunnan 650091, China)
According to the monitoring data of the road internal temperature and meteorological in asphalt pavement test section,method of cluster analysis and stepwise regression were utilized for selecting the basic indicators which could characterize the rules of pavement internal temperature and thus establishing the multiple regression equation between basic indicators and asphalt pavement temperature.Comparation of predicted values and measured values showed that the regression formula had a high precision and could be used to forecast the internal temperature of asphalt pavement.
asphalt pavement; internal temperature; meteorological data; cluster analysis; stepwise regression
2016 — 04 — 14
浙江省交通运输厅科技计划项目(2015-2-15)
谭志远(1992 — ),男,湖南双峰人,硕士研究生,主要从事路面结构与新材料的研究。
U 416.217
A
1674 — 0610(2016)04 — 0180 — 04

