静力和撞击力下钢骨混凝土桥墩位移响应研究
张 玲, 张 南, 杨 洋, 张莉杰
(南京工业大学 土木工程学院, 江苏 南京 211816)
静力和撞击力下钢骨混凝土桥墩位移响应研究
张玲, 张南, 杨洋, 张莉杰
(南京工业大学 土木工程学院, 江苏 南京211816)
通过钢骨混凝土桥墩分别在侧向集中荷载和水平撞击荷载作用下的试验,研究了静力作用下配筋方式对桥墩位移的影响;运用动力学方程,采用等效撞击力,建立了动力位移表达式,分析了型钢骨架对桥墩侧向位移的影响;结合静动力位移计算公式,得到了位移放大系数的表达式,包含了桥墩配筋参数、桥墩侧向刚度、桥墩固有频率、撞击持荷时间等主要影响因素。计算所得桥墩位移放大系数与实验结果相比符合较好,研究结果为深入研究钢骨混凝土桥墩撞击动力响应提供了一定的参考。
钢骨混凝土桥墩; 撞击力; 位移响应; 位移放大系数
0 前言
随着我国高速公路工程的迅猛发展,桥梁建设规模也不断增长。不管是跨江河桥梁还是跨线桥梁,都是公路交通运输系统中的瓶颈,它们的安全性能十分重要,但近年来经常发生汽车、船舶等撞击桥墩的事故,造成桥梁损坏、垮塌等严重后果,引起了工程界和学术界的广泛关注。很多学者对桥梁撞击问题从各个角度进行了研究,如桥墩正截面冲击承载力计算[1]、桥梁防撞设计[2]、桥墩抗船撞能力评估[3]等,取得了不少成果。为了探讨桥墩在撞击荷载下的动力响应,本文研究桥墩在静力和撞击力作用下的位移响应,探索静动位移的关系,为研究桥墩动力强度设计提供一定的研究基础。
本文对桥墩模型进行静力加载和动力撞击试验,分别研究静力作用下的位移、动力作用下的位移响应,再将静动响应进行对比,得到动力位移放大系数的计算公式。
1 试验概况
本文试验共设计2根钢筋混凝土桥墩,编号为D-1、D-2,4根钢骨混凝土桥墩编号为D-3~D-6。桥墩模型尺寸及配筋如图1和图2 所示。试验桥墩截面尺寸为200 mm×300 mm,配置4根直径为22 mm的HRB335纵向钢筋,直径为6 mm、间距为200 mm的HPB235箍筋。D — 3、D — 4在钢筋混凝土桥墩内部放置了角钢骨架,桁架上下弦杆和斜腹杆均采用∟30×3角钢,D — 5、D — 6内置槽钢骨架,上下弦杆采用6.3#槽钢,斜腹杆采用直径为16 mm的HRB335钢筋。D — 1、D — 3、D — 5为静力集中加载试验,D — 2、D — 4、D — 6利用摆锤施加水平撞击荷载,通过改变释放高度从而获得不同撞击能量。加载点(撞击点)位置为距承台上边沿400 mm处,在加载点背面放置位移计测试构件在加载过程中的位移。试验如图3所示。
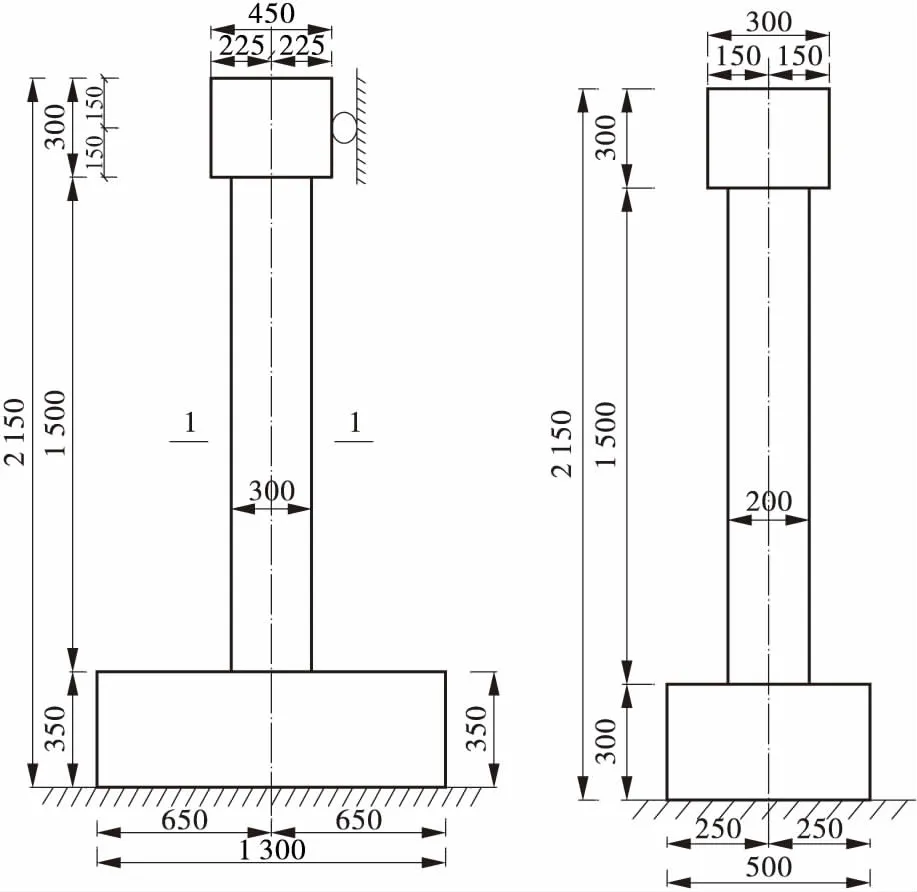
图1 桥墩模型示意图Figure 1 Diagrams of pier model
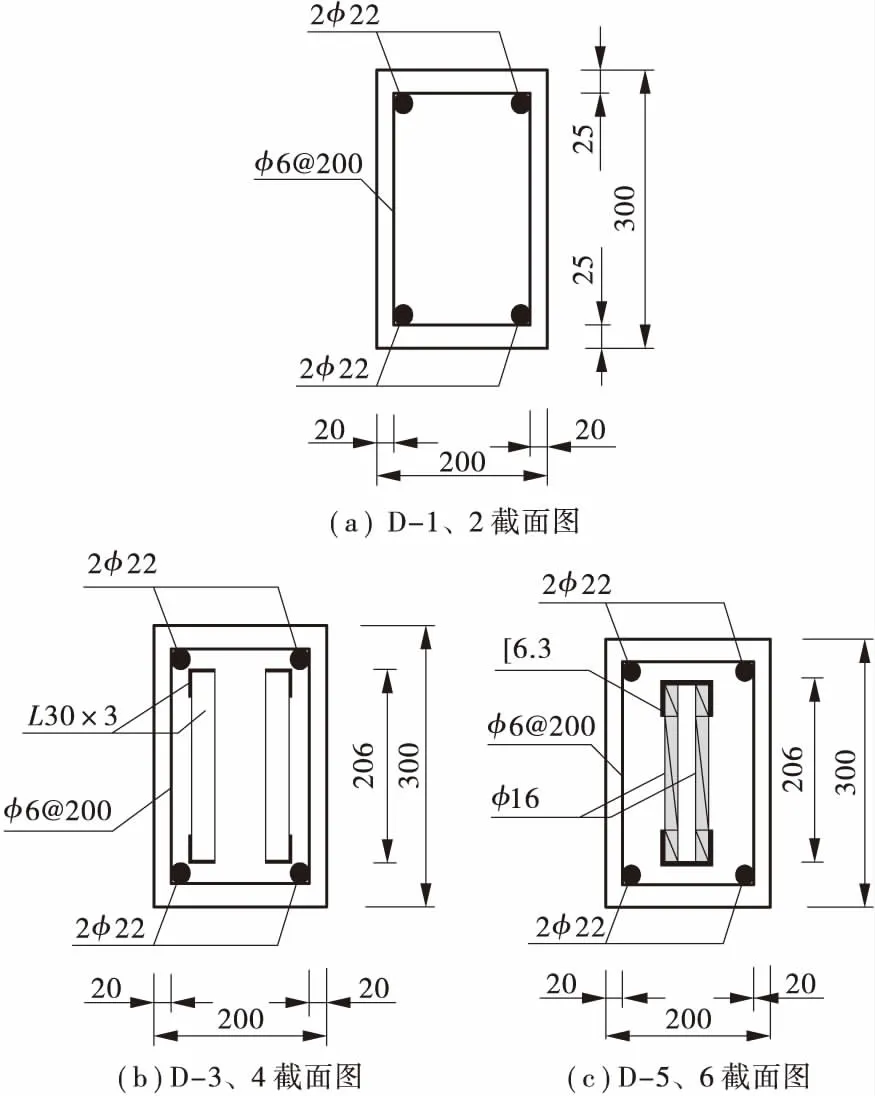
图2 横截面图Figure 2 Cross section diagram

图3 试验图Figure 3 The text figure
2 静力试验位移分析
试件D-1、D-3、D-5为静力加载实验,实验所得的荷载位移曲线如图4所示。由图可知:
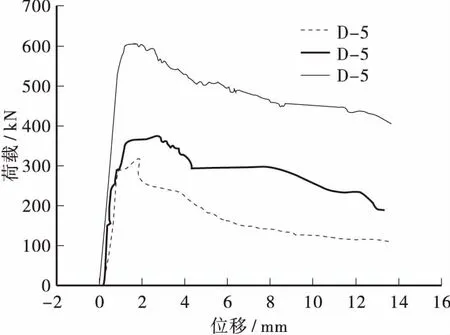
图4 荷载 — 位移图Figure 4 The diagram of load-displacement
① 当水平荷载为0时,侧向位移不为0,这是水平荷载施加前对构件施加了偏心力所致;
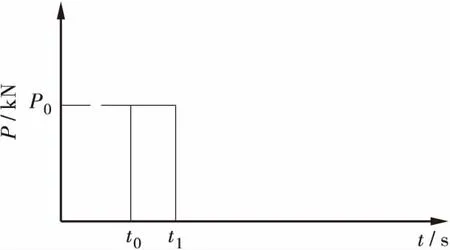
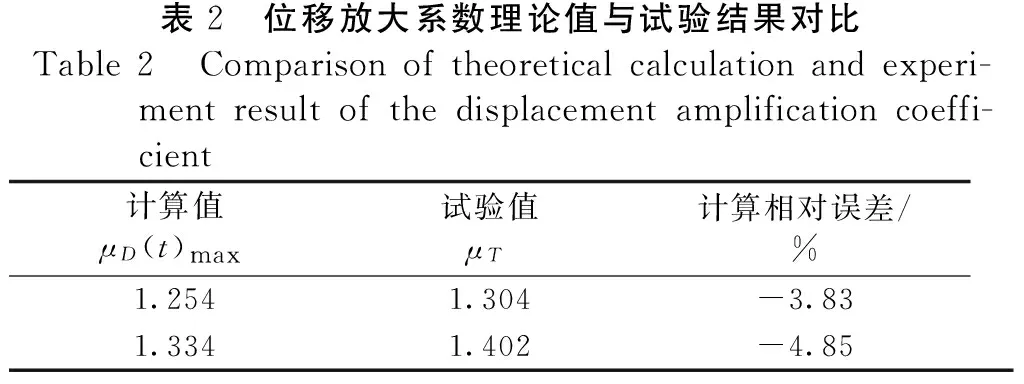
② 桥墩所能承受的极限荷载为PD-1 表1 试验结果Table1 Thetestresults墩号极限荷载/kN配筋率/%抗侧刚度(×105N·mm-1)D-13202.535.14D-33743.676.20D-56064.678.81 结构在瞬态动力作用下的响应,由于次碰撞等效应[4],使得结构内部的受力特性更加复杂,从而影响结构的动力响应,基于这些机理,对桥墩模型在撞击荷载作用下的动态分析,不应再采用静力分析方法。瞬态动力分析,也叫时间历程分析[5],是用来确定结构在随时间变化的荷载下的结构动力响应的方法。本文采用瞬态动力分析法,研究桥墩模型在撞击荷载作用下的动态位移响应。 下面采用运动微分方程法来分析桥墩模型的位移,由参考文献[6]可知:在外力f(t)作用下,单自由度体系的运动方程为: (1) 不考虑桥墩的阻尼作用,方程为: (2) 其中:m为桥墩的质量,k为桥墩的侧向刚度,u为桥墩位移。 ① 假设将撞击力(见图5)等效为阶跃力P0。 图5 阶跃力 — 时间曲线Figure 5 the curve of step force-time 方程为: (3) 由常微分方程理论可知,方程(3)的通解由相应的齐次方程的通解和非齐次方程的任一个特解组成: (4) (5) 因此可以得到最终计算结果: (6) 对式(6)进行参数分析,通过改变桥墩侧向刚度k,桥墩固有频率ω和撞击力P0得到试验桥墩的位移曲线,取前面一段,如图6所示。 图6 桥墩位移计算值分布曲线Figure 6 The calculated value distribution curve of pier displacement 通过图6定性的分析可知:当D — 4、D — 6加入型钢骨架时桥墩的侧向刚度依次增加,在相同撞击能量下,撞击产生的位移均小于钢筋混凝土桥墩D-2所产生的位移,该分析结果符合本文试验的位移测试结果。 ② 假设将撞击力时程曲线等效为三角波函数[7]。 由Duhamel积分可得式(2)的解为: (7) 由于撞击荷载的破坏性巨大,已将它作为结构设计的控制因素。本文将试验所得撞击荷载-时间曲线(见图7)等效为三角波,如图8所示,得: (8) 图7 撞击力 — 时间曲线图Figure 7 the curve of impact force-time 图8 等效力 — 时间曲线Figure 8 the curve of equivalent force-time 将式(8)代入式(7),通过积分得到位移的计算公式为: 定义撞击荷载作用下,桥墩的位移放大系数μD表达式为: (10) 其中:u(t)为三角波撞击力时程下的动态位移;ust为三角波峰值力作用下的静力位移,可表示为: (11) 假设本文试验的桥墩模型为无阻尼系统,位移响应只与桥墩模型的固有频率和所承受撞击力的作用时间有关。通过式(9)~式(11),可得位移放大系数的表达式为: (12) 文献[8]在研究冲击荷载作用下的结构设计方法时,分别求得静、动作用下的位移表达公式,定义λ(t)为动态响应位移与对应峰值力作用下位移的比值,通过分析研究后得到λ(t)的最大值仅与结构的固有频率和撞击力作用时间有关,可表达为: (13) 其中:t1为撞击力达到峰值所用时间,ω0为结构的固有频率。 运用此公式,可得本文位移放大系数最大值的计算公式为: (14) 定义试验位移放大系数计算公式为: (15) 其中:uTmax为试验所得桥墩模型位移时程峰值;uTst为uTmax同工况下撞击力时程峰值作为静力值,再对应静力试验所得静力位移。 某一撞击工况下,测得桥墩模型的位移峰值uTmax为0.639 mm,此时撞击力时程峰值为185 kN; 静力作用下,185 kN对应的静位移为0.49 mm,代入公式(15)可得试验位移放大系数μT为1.3041,另取一个工况,同理可得相应的试验位移放大系数。 将计算值与试验值进行对比,如表2所示。从表2可见,计算结果与试验结果符合较好,计算相对误差小于5%, 表明本文采用的瞬态动力分析方法用于桥墩撞击动力位移响应分析是合理可行的。 表2 位移放大系数理论值与试验结果对比Table2 Comparisonoftheoreticalcalculationandexperi-mentresultofthedisplacementamplificationcoeffi-cient计算值μD(t)max试验值μT计算相对误差/%1.2541.304-3.831.3341.402-4.85 本文在试验的基础上,对钢筋混凝土桥墩和钢骨混凝土桥墩分别在水平静力集中荷载和水平撞击荷载作用下的位移响应进行分析,主要结论有: ① 在试验桥墩内部配置钢骨,能抑制裂缝的产生和发展,使得桥墩的侧向位移减小,且随钢骨形式不同而异,配置槽钢的桥墩比配置角钢的桥墩侧向位移小。 ② 运用动力学方程,将撞击力等效为阶跃力,得到理论计算的位移时程曲线,与实验所得曲线符合较好,这为分析桥墩受到撞击力作用下的位移响应提供了一种可行的方法。在相同撞击能量下,不同类型的钢骨会影响桥墩的动位移响应。 ③ 对动力学方程进行Duhamel积分,结合本文试验的撞击力时程曲线,将曲线简化为三角波函数,得到了位移计算公式,其中包含了撞击力峰值、桥墩固有频率、桥墩侧向刚度、桥墩配钢率、撞击持荷时间等因素的影响。 ④ 分析本文所建立的位移放大系数最大值的表达式,可得影响位移放大系数最大值的主要因素有:桥墩侧向刚度、桥墩固有频率和撞击持荷时间。将本文公式计算出的位移放大系数最大值,与试验求得的结果相比,符合较好,表明本文所建立公式合理,这为进一步研究桥墩侧向荷载下的静力性能与撞击动力响应关系提供了一定的参考。 [1]樊文才,张南,许琦.钢筋混凝土圆形桥墩正截面冲击承载力计算 [J].公路工程,2010,35(1):107-112. [2]卢绍鸿,惠州范和港跨海大桥设计特点 [J].公路工程,2013,38 (3):151-154. [3]钱长根,刘伟庆,方海,等.吴淞江大桥桥墩抗船撞能力评估研究 [J].公路工程,2014,39(6):61-65. [4]田阿利,尹小春.考虑桩-土-锤相互影响的基桩瞬态动力响应 [J].工程力学,2012, 29(11):283-288. [5]贾宏宇,刘作飞,田建柱,等.船舶撞击下的内河框架码头瞬态响应分析 [J].人民长江,2010,41(17):283-288. [6]刘延柱,陈文良,陈立群.振动力学[M].北京:高等教育出版社,1998. [7]阎石,刘蕾,齐宝欣,等.爆炸荷载作用下方钢管混凝土柱的动力响应及破坏机理 [J].防灾减灾工程学报,2011,31(5):477-482. [8]王江,吴德隆.冲击荷载作用下的结构设计方法 [J].导弹与航天运载技术2007 (3):33-37. [9]廖小军.船舶侧向撞击桥梁基础的动力放大系数探讨 [J].公路交通技术,2009 (3):78-82. Research on Displacement Response of Steel Reinforced Concrete Bridge Piers under Static Load and Impact Load ZHANG Ling, ZHANG Nan, YANG Yang, ZHANG Lijie (College of Civil Engineering, Nanjing Tech University of Technology, Nanjing, Jiangsu 211816 China) The effects of the reinforcement ways of steel reinforced concrete bridge piers on their displacements are studied in this work based on the tests in which the piers were loaded under lateral concentrated load and horizontal impact load respectively. The dynamic displacement expression is established by applying equivalent impact force in the kinetic equations, and the influences of section steel framework on the displacement of piers are analyzed. Using static and dynamic displacement formulas, the expression of the amplification coefficients of displacement are obtained, in which the main factors, such as the reinforcement parameters, bridge piers stiffness, natural frequency of bridge piers, actuation duration of impacts, are included. The calculated amplification coefficients are proven to fit the experimental results well. The results of this study provide certain references for further research of dynamic responses of steel reinforced concrete bridge piers under impact force. steel reinforced concrete pier; impact force; displacement response; displacement amplification coefficient 2015 — 10 — 27 国家自然科学基金资助(51278243) 张玲(1989 — ),女,江苏南通人,硕士研究生,研究方向为桥梁结构动力性能。 U 441+.2 A 1674 — 0610(2016)04 — 0037 — 05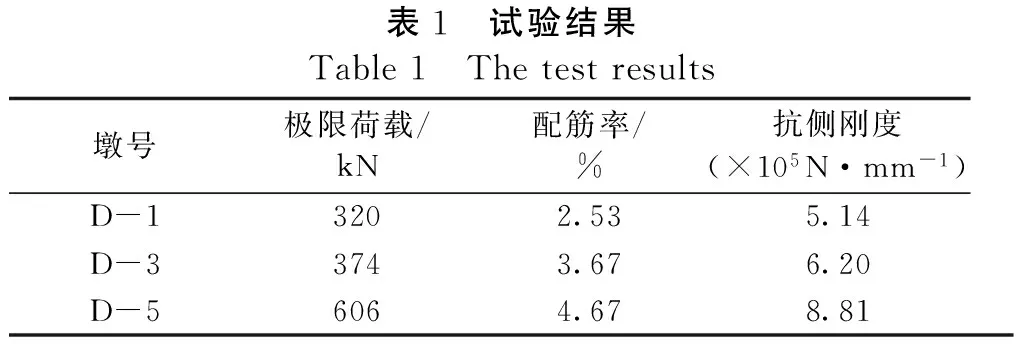
3 动力试验位移分析

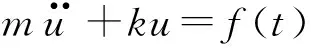
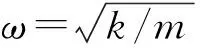
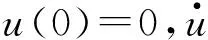
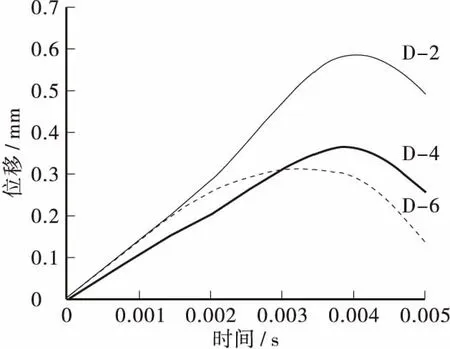
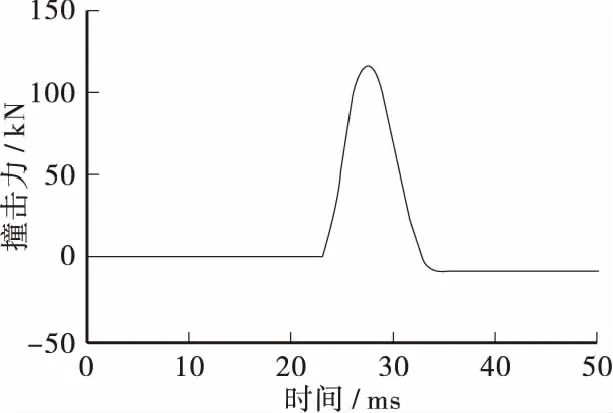
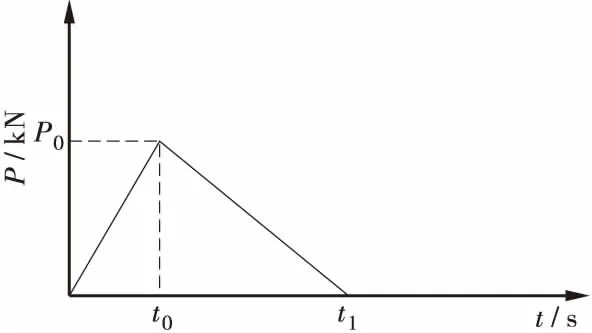
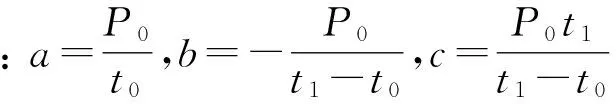
4 动力放大系数研究
5 算例分析
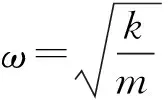
6 结论

