规则波的波浪参数对深水桥墩波浪力的影响分析
左生荣, 谭博夫, 杨吉新
(1.湖北省路桥集团有限公司, 湖北 武汉 430056; 2.武汉理工大学 交通学院, 湖北 武汉 430063)
规则波的波浪参数对深水桥墩波浪力的影响分析
左生荣1, 谭博夫1, 杨吉新2
(1.湖北省路桥集团有限公司, 湖北 武汉430056;2.武汉理工大学 交通学院, 湖北 武汉430063)
针对波浪对深水桥墩的作用,不同波浪参数的形式对深水桥墩波浪力的影响大小和程度各不相同,这就需要对深水桥墩在设计和施工阶段需要采取有效的应对方法。以CFD数值计算的方法为基础,对大直径圆形的深水桥墩在不同波长和波高的三维波浪参数条件下受到的波浪力分别进行了计算,并得到了各自的大小,数值计算结果表明波长和波高的规则的增长,波浪力也基本上呈规则的变化,并且波浪力在墩柱自由水面下垂直深度方向的分布上是逐步减小的,到达某一深度减小为零,同时波长和波高的增加都会扩大波浪力在墩柱上的影响范围。
规则波; 波浪参数; 大尺寸桥墩; 波浪力
1 概述
随着国内跨海大桥的建设迅猛发展,对于桥梁水下结构的桥墩与流体的流固耦合研究取得了长足的进展,目前使用较多的是CFD数值计算方法[1]。在跨海桥梁的环境影响因素中,海浪对桥墩的作用是及其普遍的,其影响也是巨大的,因此对不同形式的波浪对桥墩的作用力的研究显得尤为关键[2]。在理论研究中,规则波的形式是一种常见的形式,通过规则波浪对桥墩的作用来找到波浪力的规律,以此找到跨海大桥桥墩的结构设计的相应的对策。另外,在深水桥墩的承台施工中广泛采用钢围堰的施工形式[3,4],施工中波浪与钢围堰的作用对结构的受力和施工的安全起到非常关键的作用,因此研究不同类型的波浪形式对波浪力的影响规律是非常必要的[5]。
2 CFD数值计算方法介绍
在计算波浪力的各种方法中,CFD数值计算方法是研究波浪和墩柱结构一种行之有效的方法。该方法在近些来得到了迅猛发展,其核心就是依赖于计算机技术、数值计算技术的发展而发展起来的一门学科,该法可以运用强大的计算机仿真系统,可以模拟现实的流体情况,研究其对结构产生的作用[6]。该方法在越来越多的工程应用中得到应用和发展并取得跟理论方法和试验方法较为接近的结果。本文以CFD数值计算方法作为研究波浪与墩柱结构作用的主要手段,通过改变波浪的参数来进行数值计算,再对结果进行分析,找出两者在相互作用过程中的规律,最终找出对结构的安全影响较大的因素。
本文选取的圆形桥墩截面直径D为4.0 m,墩高H为30 m,水深(自由面)20 m,桥墩材料如表1所示。波长是10 m,波高是0.4 m,波浪周期T为2.53 s,数值方法中海水体密度为 1030 kg/m3。传播方向从左至右沿x轴正方向。

表1 圆形墩柱材料参数表Table1 Materialparametertableofcircularpiercolumn参数数值墩柱密度(ρp)/(kg·m-3)2550弹性模量(E)/Pa3.1×1010泊松比(γ)0.2
2.1计算参数设置
在有限元理论上,对于计算域的边界条件一般取无穷远处,但受限于计算条件,一般假定对于流体水槽的计算域的选择一般是假定结构距入口和出口距离都是5D(D表示圆形墩柱体横截面的直径),本模型为了保证流体的运动得到充分的发展,取值的范围是10D[7]。
运用ANSYS workbench中FLUENT模块进行建模计算,水槽的计算域为60 m×40 m×32 m,网格划分如图1,图2所示。

图1 圆形墩柱截面网格示意图Figure 1 Grid schematic diagram of circular pier column section

图2 计算域网格效果整体示意图Figure 2 Schematic of the computational domain grid effect
2.2波浪与圆形墩柱作用
图3给出了一个波浪周期内波浪与大直径圆形墩柱相互作用的的波面变化图,由图可以看出: 波浪从开始出发到波峰和波谷分别经过圆形墩柱时的情况。波浪从左至右沿x轴正方向传播。


图3 某时刻波浪与圆形墩柱相互作用的波面变化图
Figure 3Wave surface change maps of wave and circular pier column interaction at a certain time
2.3大直径圆墩上波浪力分析
通过计算可以求得不同时刻作用在直径4 m圆形墩柱上的波浪力,把水平方向的波浪力绘成如图4所示的波浪力时程曲线。从图中可以看出波浪从开始进入到经过大约5 s后趋于稳定,波浪力的振幅整体上保持在一个稳定的范围内[8]。波峰作用时最大波浪力是23187.9 N,为正值;波谷作用时的最大波浪力是-23880 N,为负值。波浪力的周期与波浪周期基本保持一致[9,10]。
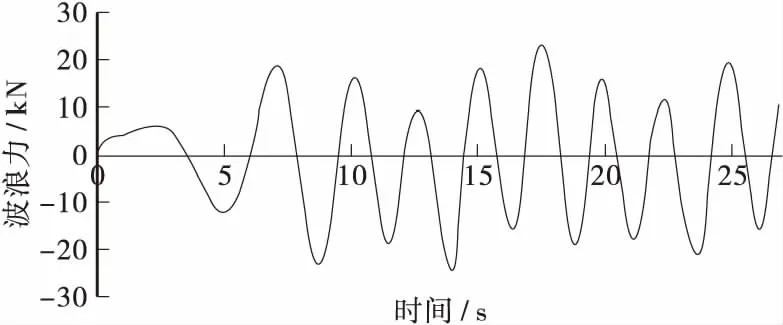
图4 大直径圆形墩柱x方向波浪力时程曲线Figure 4 Time-history curve of X direction wave force on large diameter circular pier column
3 波浪参数对波浪力影响的分析
对于规则线性波浪,波浪参数主要体现在波长和波高上,波长和波高对波浪力大小的影响程度决定波浪参数对墩柱结构设计的重要性。下面分别研究规则波参数中波长和波高的变化对波浪力的影响以及变化规律。
3.1波长对波浪力的影响
为了分析波长对波浪力的影响,在10 m波长的计算基础上,在其它波浪参数不变的情况下分别把波长变为14 m和18 m。然后分别计算其作用在圆形墩柱上波浪力的大小。
波长分别为14 m和18 m时,圆形墩柱受到的水平方向波浪力的时程曲线如图5,图6所示。

图5 波长14 m时水平方向波浪力时程曲线Figure 5 Time-history curve of the horizontal wave force on the wave length of 14 m
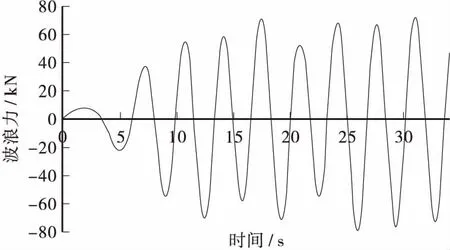
图6 波长为18 m时水平方向波浪力时程曲线Figure 6 Time-history curve of the horizontal wave force on the wave length of 18 m
从图5,图6中可以看出: 波长为14 m时波峰最大波浪力是51993 N,波谷最大波浪力为-51477.3 N;波长为18 m的规则波作用时的波峰最大波浪力是72931.6 N,波谷最大波浪力是-79099.2 N。
通过计算可发现,在其它参数不变的情况下,波长从10 m增加至14 m,波峰的波浪力最大值增加了55.4%,波谷的波浪力最大值增加了53.6%;波长从14 m增加至18 m时,波峰的波浪力最大值增加了40.3%,波谷的波浪力最大值增加了53.7%,波长变化对波浪力的影响是比较显著的,并且同一波长的波峰与波谷的最大波浪力变化率基本保持一致。
由图9可以看出:波长和波浪力的变化关系,波浪力与波长在一定的范围内呈现出线性变化规律。
3.2波高对波浪力的影响
为了分析波高对波浪力的影响,在其它参数不变的情况下,把波高分别增加至0.6 m和0.8 m,然后分别计算其对圆形墩柱产生波浪力的大小。
波高是0.6 m和0.8 m时,作用于墩柱上水平波浪力的时程曲线,见图7,图8。
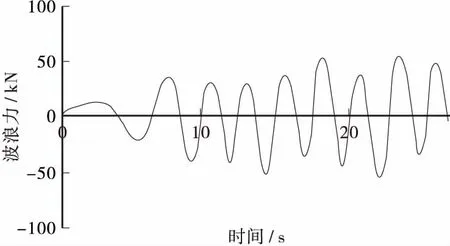
图7 波高0.6 m时水平方向波浪力的时程曲线图Figure 7 Time-history curve of the horizontal wave force on the wave height of 0.6 m

图8 波高0.8 m时波浪力时程曲线图Figure 8 Time-history curve of the horizontal wave force on the wave height of 0.8 m
从图7,图8中可以看出: 当波高为0.6 m时,波峰作用于圆形墩柱的最大波浪力是55317.8 N,波谷作用时最大波浪力是-54663.3 N。相比波高是0.4 m(其它参数不变)时的波浪力,波峰最大波浪力增加了138.6%,波谷最大波浪力增加了128.9%。当波高是0.8 m时,波峰作用于圆形墩柱时的最大波浪力是101553.6 N,波谷作用时最大波浪力是-90282 N。相比波高是0.6 m(在其它条件一致)时的波浪力,波峰最大波浪力增加了83.6%,波谷最大波浪力增加了65.2%。变化规律见图9所示。波浪力与波长在一定的范围内呈现出线性变化规律。
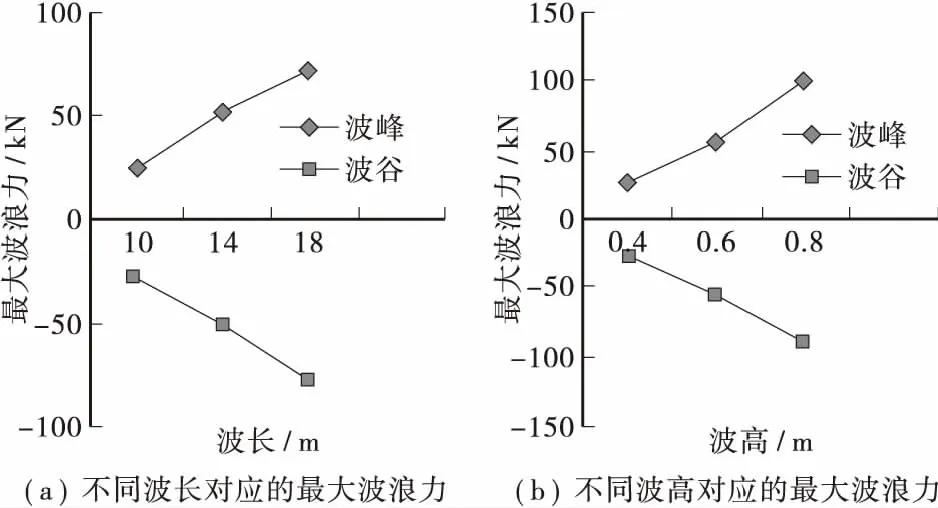
图9 不同波长和波高对应的最大波浪力图Figure 9 The maximum wave graph corresponding to different wave length and wave height
4 波浪力在桥墩深度上的分布规律
选取参数波长是10 m,波高是0.4 m的波浪与圆柱作用时,墩柱上不同深度上对应的波浪力建立如图10、图11所示的坐标系,得到波浪力随深度变化的曲线。
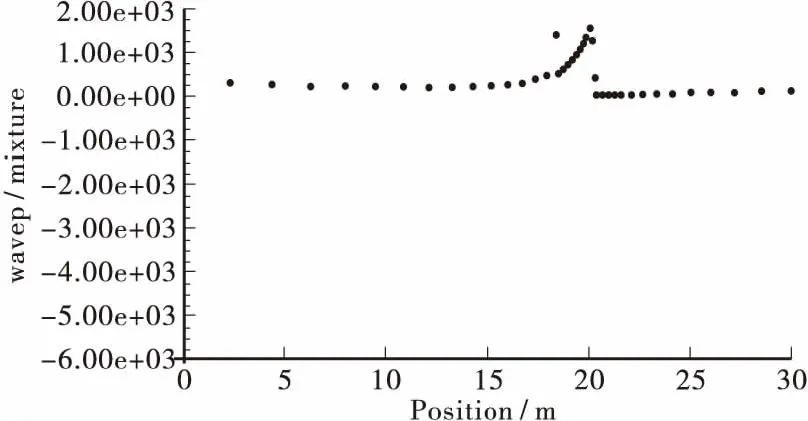
图10 波峰作用时波浪力随水深的变化图Figure 10 The wave force change chart with the depth when wave peak function
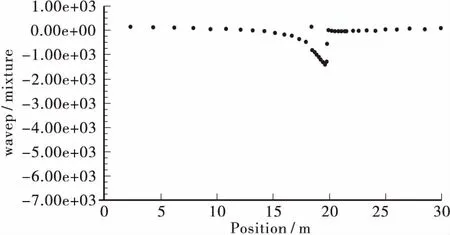
图11 波谷作用时波浪力随水深的变化图 Figure 11 The wave force change chart with the depth when wave trough function
从图10中可以看出: 当波峰作用于墩柱时,在距离墩柱底部越高的迎浪侧处,波浪力越大,产生最大波浪力的位置是在距离墩底部大约20.4 m的墩柱迎浪侧上。波浪力在沿墩柱深度上越接近墩底的位置越小,一直到距离墩底大约15 m的位置上,此位置上的波浪力与最大波浪力相比可以忽略不计,在此深度以下各点的波浪力几乎为零,说明波浪力在该深度以下对墩柱几乎没有影响。波浪力从最大到零的深度范围是从距离墩底20.4 m到距离墩底15 m的约5.4 m的区域。波谷作用于墩柱时的情况如图11所示。
波高和波长变大后,其对波浪力在桥墩深度上的分布规律与之前一致。以波高是0.6 m和波长是14 m时的规则波作用时为例进行说明,在波峰作用下,墩柱上波浪力的分布情况如图12、图13所示。
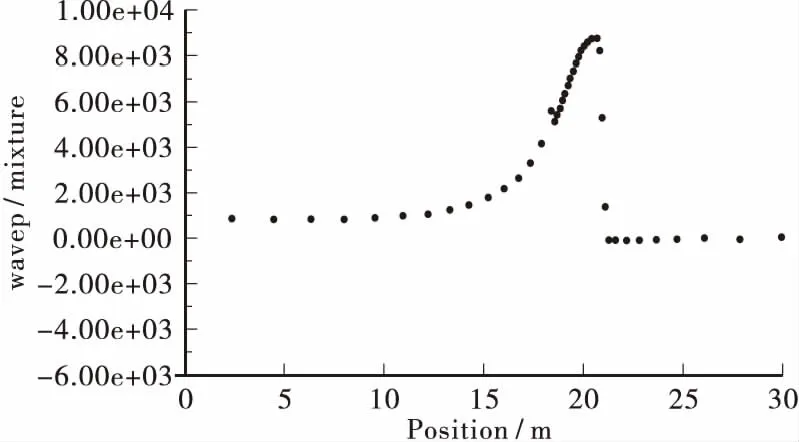
图12 波高0.6 m作用时波浪力随水深的变化图Figure 12 The wave force variation map with water depth at wave height 0.6 m

图13 波长14 m作用时波浪力随水深的变化图Figure 13 The wave force variation map with water depth at wave length 14 m
通过图12、图13可以看出: 波浪参数的波长和波高变大后,波浪力在圆形墩柱垂直深度上的影响范围也增大了。
这在深水桥墩下构施工时,针对波浪力对诸如钢围堰等深水结构的影响可采取有效的措施加以防范和改进,具有积极的现实意义[11]。
5 结论
本文研究了海洋工程中大尺度墩柱结构在各种波浪作用下的规律,总结如下:
① 作用在墩柱上的水平方向波浪力的时程曲线与波浪周期基本一致,在一个周期内,波峰作用于墩柱时出现正值的最大值,波谷作用时出现负值的最大值。
② 改变波长和波高两个波浪参数,结果显示波长分别是14 m和18 m(基本模型波长是10 m)的波峰的最大波浪力比波长是10 m和14 m 时分别增大了55.4%和40.3%;波谷的最大波浪力比波长是10 m和14 m 时分别增大了53.6%和53.7%;当波高分别为0.6 m和0.8 m(基本模型波高是0.4 m)的的波峰最大波浪力比波高为0.4 m和0.6 m时分别增大了138.6%和83.6%;波谷的最大波浪力比波高为0.4 m和0.6 m时分别增大了128.9%和65.2%。在一定范围内波长和波高的变化与波浪力的变化近似的呈线性关系。
③ 波浪力在墩柱垂直深度上的分布规律:从自由液面由上向下沿着墩柱逐渐减小,在距离墩底某个深度后波浪力趋于零,波浪力从最大值到零的这个深度范围较小,只占整个墩柱的长度较小的一部分,并且随着波长和波高的变大,这个深度的影响范围也相应增大。
[1]李玉成,何明.作用于小尺度方柱上的正向波浪力[J].海洋学报:中文版,1996,18(3):107-119.
[2]左其华.方形墩柱上的非线性波浪荷载[J].海洋工程,1993,(1):50-57.
[3]杨永伟,戴桂华.张花高速酉水大桥5号主墩深水双壁钢围堰施工技术[J].公路工程,2013,38(5):193-198.
[4]杨永伟,戴桂华.张花高速酉水大桥深水桩基施工技术[J].公路工程,2013,38(5):199-203.
[5]赖华威,刘月琴,吴家鸣.基于CFD方法的螺旋桨性能计算与分析[J].船海工程,2009(04):131-135.
[6]阎超,于剑.CFD模拟方法的发展成就与展望[J].力学进展,2011,41(5):562-589.
[7]杨吉新,雷凡.水下桥墩结构的振动分析[J].世界桥梁,2009(3):40-42.
[8]俞聿修,张宁川,赵群.三维随机波浪对桩柱的作用[J].海洋学报,1998,20(4):121-132.
[9]严开,邹志利,李献丽.不同二阶绕射波浪力理论公式的结果互比[J],工程力学,2013(4):31-37.
[10]祝兵,宋随弟,谭长建.三维波浪作用下大直径圆柱绕流的数值模拟[J].西南交通大学学报,2012(2):224-229.
[11]李柏殿,刘礼辉.悬臂导向架在深水基础施工中的应用[J].公路工程,2012,37(4):160-162.
Deep water Piers'wave Forces Effect Analysis of Regular Wave Parameters
ZUO Shengrong1, TAN Bofu1,YANG Jixin2
(1.Hubei Provincial Road & Bridge CO.,LTD, Wuhan, Hubei 430056, China;2.School of Transportation,Wuhan University of Technology,Wuhan, Hubei 430063, China)
In view of the waves action with deep water piers, according to different wave parameters,the wave force influence is not identical, this problem needs take effective methods to solve in design and construction stage.In this paper, based on the method of CFD numerical simulation, the wave force of deep water piers under the different wave parameters condition is calculated respectively, and the value of the respective wave force is calculated.The numerical calculation results show that the wave force presents basically a rule change with the rules growth of wave length and wave height. Alone the free surface to the bottom of the pier,the wave force is gradually decreasing.Until reached to a certain depth,the wave force decreases to zero.At the same time,the wave force will expand the scope on the pier increasing the wave length and wave height.
regular wave; wave parameters; deep water pier; wave force
2015 — 03 — 11
国家高技术研究发展计划(863)项目(2007AA11Z107)
左生荣(1978 — ),男,江苏姜堰人,工学博士,高级工程师,从事桥梁结构物的诊断与加固。
U 443.22; TV 312
A
1674 — 0610(2016)04 — 0028 — 04

