基于多元联系数集对分析的航空维修风险态势评估

施志坚，王华伟，王 祥（南京航空航天大学民航学院，江苏　南京211106）

基于多元联系数集对分析的航空维修风险态势评估

施志坚，王华伟，王 祥
（南京航空航天大学民航学院，江苏南京211106）

为提高航空维修风险评估的有效性，引入多元联系数集对分析理论，将评估系统中的确定与不确定因素作为一个整体进行处理。在考虑专家权重的基础上，运用不确定层次分析法确定各评估指标的权重区间，并通过三元联系数的联系度表达式将权重区间转化为权重精确值。对三元联系数的不确定项进行拓展得到五元联系数表达式，以此为基础建立风险的同异反评估模型。根据由该模型计算出的集对势结果对系统风险态势进行评判，并利用各阶偏联系数对风险发展趋势进行分析，实现静态和动态评估的有效结合。以某航空公司维修基地为实例，计算和分析结果表明了该方法在系统风险评估及趋势分析中的可行性与有效性。

航空维修；集对分析；多元联系数；风险评估

网址：www.sys-ele.com

0 引 言

随着我国民航业的快速发展以及航空公司和旅客对航班正常率要求的不断提高，维修人员的工作压力不断增大，易导致航空维修事故的发生。根据近20年的事故调查数据统计，维修差错导致的航空事故增加了4个百分点，世界上20%～30%的空中停车、50%的航班延误、50%的航班取消的原因集中在维修差错事件上面［1］。此外，国内航空维修人员预计到2020年要增加至20万人，维修安全管理水平_亟_待_提_高_。因此，深入展开航空维修系统的安全风险评估研究工作，对于降低航空维修事故率、提高飞行安全水平具有重要意义。

目前，国内对于航空维修系统的安全风险评估研究已取得一些成果：文献［2］利用模糊综合评价法对影响航空维修安全和质量状况的指标进行定量化处理；文献［3］通过因子分析法确定了导致维修差错的主要诱因；文献［4］提出了一种基于H F A CS-M E框架和灰色关联分析法的航空维修差错模式和差错成因之间关系的分析方法；文献［5］基于熵权法和全决策树法分析维修安全主要影响因子对维修人误概率的影响程度；文献［6］将贝叶斯网络引入民航维修人因安全分析研究中，找到了系统薄弱环节。这些方法在航空维修风险评估中起到了一定作用，但未能同时考虑和处理系统中诸多确定和不确定因素，也无法对风险趋势作出有效预测和分析。

集对分析法（set pair analysis，SP A）是从系统的角度去认识确定和不确定因素的关系，并认为研究对象是一个确定不确定的系统，目前该理论已在矿业、交通、环境等诸多领域得到应用［7 11］。作为一个复杂的人机系统，航空维修系统中以人为中心，各种因素相互作用、相互依存，使其具有模糊性、随机性、灰色性等不确定特征［12 13］。因此，本文将多元联系数集对分析引入航空维修风险评估中，并结合不确定层次分析法确定指标权重，以期实现对航空维修系统的静态和动态研究。

1 多元联系数集对分析

1.1 集对分析与联系度

集对分析［14］是对确定不确定性系统中的两个有关联的集合构造集对，通过建立集对的同、异、反联系度，对集对的某特征进行同一性、差异性、对立性分析的研究方法。

给定2个集合A和B，并设这2个集合组成的集对H= （A，B），A和B都具有N个表征特性，其中2个集合有S个共同特性，P个相对立特性，F个既不共有也不对立的特性，F=N-P-S。若令：a=S/N，b=F/N，c=P/N，则该集对的联系度（常称为同异反联系数或三元联系数）可表示为［15］

式中，μ为联系度；a为同一度；b为差异度；c为对立度，a，b，c∈［0，1］，且a+b+c=1；i为差异标记符号，i∈［-1，1］；j为对立标记符号，j≡1。

1.2 五元联系数与集对势

由于三元联系数中bi项能够同时体现不确定联系可以在一定条件下确定和一般条件下不能确定的两面性，在实际应用中，常将该项进行剖析拓展至多元联系数，其一般表达式为［16］

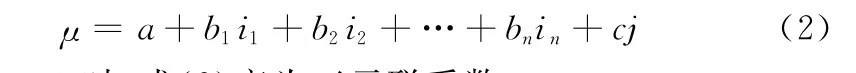
当n=3时，式（2）变为五元联系数

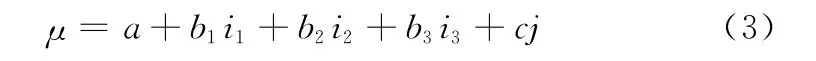
式（3）常简记为

式中，a，b，c，d，e∈［0，1］；i∈［0，1］；j∈［0，0］为中性标记，不作j=0解，k∈［-1，0］，l=-1；a，b，c，d，e具有层次性，a≻b≻c≻d≻e，“≻”读作“正于”，且a+b+c+d+e=1。

1.3 偏联系数

多元联系数的偏联系数表示了其同异反确定不确定联系状态的发展趋势，其中，五元联系数的各阶偏联系数分别为［17］

一阶偏联系数：

二阶偏联系数：

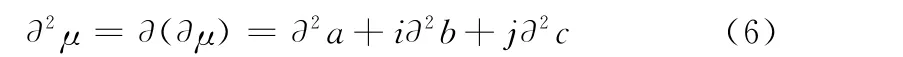
三阶偏联系数：

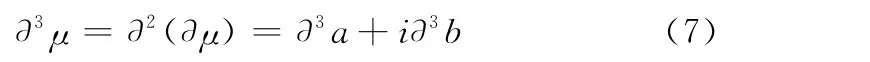
四阶偏联系数：

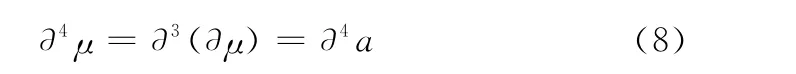
在计算偏联系数值时，为保证评判结果的可靠性和可信性，本文在最“保守”的情况下的对各联系数分量进行取值。计算一阶偏联系数时，取i=0，j=0，k=-1；计算二阶偏联系数时，取i=-1，j=-1；计算三阶偏联系数时，取i=-1。当计算结果i（μ）＞0时，呈现提高趋势，表明研究对象状况转好，风险降低；当i（μ）＜0时，呈现下降趋势，呈现降低趋势，表明研究对象状况变差，风险增高；当i（μ）= 0时，呈现中介不确定趋势，表明研究对象存在提高和下降兼有的中间过渡趋势。

2 基于多元联系数集对分析的航空维修风险态势评估模型

2.1 建立航空维修风险评估指标体系

本文统计了2000-2009年间关于国内民航维修的73起事故征候，对事故致因进行了详细调查和分析，结合航空维修生产活动的特点和文献［18-19］，对影响维修安全水平的因素进行分类和筛选，从而建立出航空维修风险评估指标体系，如表1所示。

表1 航空维修风险评估指标体系

2.2 确定各级评估指标权重

2.2.1 利用不确定层次分析法求取指标权重区间

由于航空维修系统的复杂性各，风险因素相互依存、相互作用，使其具有一定的随机性和模糊性，因此采用不确定层次分析法［20］来描述专家对各风险因素之间相对重要度的评判。

假设某级指标体系中有n个风险指标，各专家采用1～9比例标度法对风险指标之间的相互重要度进行两两比较，形成区间数及判断矩阵A：

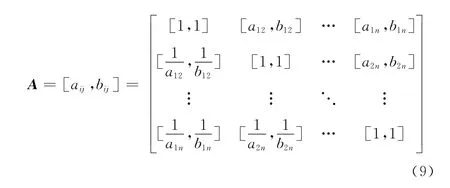
由判断矩阵A计算得到满足互反性的一致性判断矩阵M=（mij）n×n：

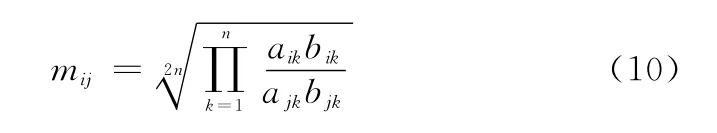
由此可求得一致性判断矩阵M的权重向量Wi=（w1，w2，…，wn）：

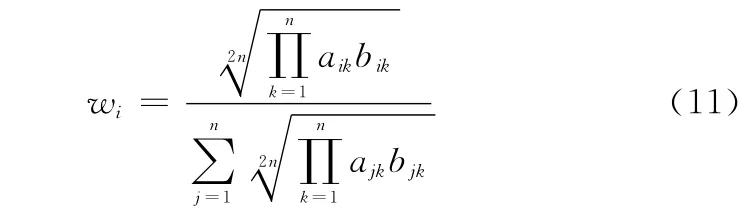
考虑到两个判断矩阵M和A计算出的权重之间存在误差，令Δ1mij=mij-aij，Δ2mij=bij-mij，可得

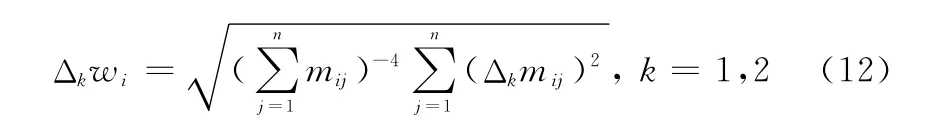
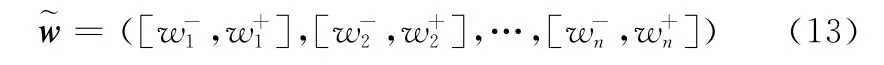
2.2.2 利用三元联系数求取指标权重

由于不确定A H P法只能获得各评估指标的权重区间，不能得到精确值，因此引入三元联系数从同、异、反3个方面分别描述指标的权重区间值，并将其转化为定值。由于［0，1］，将权重区间与区间［0，1］建立集对，其三元联系数表示为

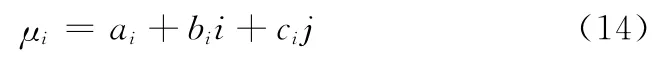
式中：ai=表示确定能够达到的程度；bi=-表示不能确定达到的程度；ci=1-表示确定不能达到的程度。

可以计算出确定性区间的相对权重pi与不确定区间的相对权重q［21］：

i

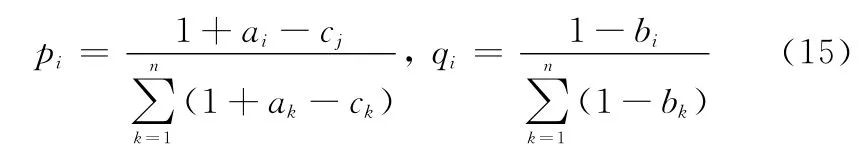
最后得到各评估指标的精确权重值w*=（，，…，）：

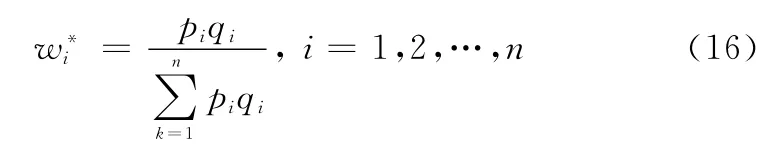
2.3 构建风险的同异反评估模型

将各评估指标与有关风险标准对比，并与五元联系数的系数分量相对应，按其与标准的相符程度将风险集U= ｛u1，u2，u3，u4，u5｝分为：“低风险”、“较低风险”、“中等风险”、“较高风险”、“高风险”五级评语。

利用公式Rij=Nij/N（Nij为将评估指标i归为风险等级j的专家人数，N为评估专家总数），对各评估指标发生的严重程度和发生概率进行估计。结合式（16）计算出的各评估指标权重与五元联系数式（4），得到风险的同异反评估模型：

简记为

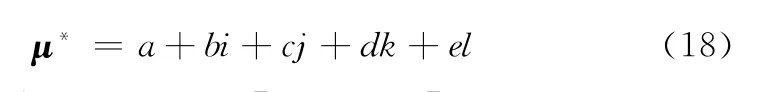
式中，μ*为综合联系度；F=［1，i，j，k，l］为系数矩阵；根据集对分析理论可知为同一测度分量，表示指标属于“低风险”的程度差异测度偏同分量，表示指标属于“较低风险”的程度为差异测度居中分量，表示指标属于“较低风险”的程度；d=为差异测度偏反分量，表示指标属于“较高风险”的程度为对立测度分量，表示指标属于“高风险”的程度。其中a，e为确定项；b，c，d为不确定项。

2.4 风险的态势及趋势分析

由于集对势可反映2个集合在特定问题背景下的某种联系趋势，可根据五元联系数中a，b，c，d，e的数值大小关系，将系统风险分为：“同势”，即Shi（μ）＞1；“均势”，即Shi（μ）= 1；“反势”，即Shi（μ）＜1。在此基础上计算出五元联系数的各阶偏联系数，对风险的发展趋势进行深入分析。基于篇幅，表2中仅给出与本文工程实例有关的五元联系数同势态势排序，完整的态势表见文献［22］。

当系统态势为“同势”时，表示系统风险与理想标准状态具有同一趋势，即“低风险”，可通过分析各阶偏联系数，重点关注处于“反势”态势的子评估指标，确保系统能够维持低风险状态；当系统态势为“均势”时，表示系统风险与理想标准状态呈现“势均力敌”趋势，即“中等风险”，根据各阶偏联系数计算结果，加强管理处于“反势”态势的子评估指标，促使系统风险不断降低；当系统态势为“反势”时，表示系统风险与理想标准状态具有相反对立趋势，即“高风险”，同样利用各阶偏联系数，集中力量整改处于“反势”态势的子评估指标，逐渐修正系统的安全水平。

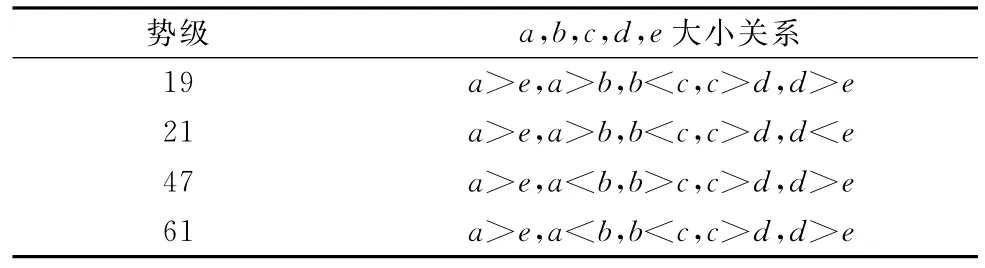
表2 五元联系数系统同势态势表

3 实例分析

针对我国某航空公司某维修基地的风险评估项目，聘请现场维修人员A、维修技术专家B、维修管理人员C以及维修领域学者D各一位。考虑到各位评估人员的学术水平、工作实践经验等条件有所差别，结合各位评估者的职称、工作时间、对系统工程理论的熟悉程度以及对该维修基地的了解程度等情况，为4位评估人员赋予权重：

3.1 计算风险评估指标权重

以一级指标“人的因素u1”为例，说明其具体计算过程。4位评估人员根据1～9比例标度法对“人为因素u1”所对应的各二级指标“技能和经验u11”、“安全意识u12”、“注意力与警觉性u13”、“健康与疲劳u14”、“社会/家庭关系u15”进行两两比较，给出的区间数与判断矩阵A（k）（k=1，2，3，4）如下所示：

考虑各评估人员的权重w′，利用式（19）对判断矩阵A（k）进行修正：

根据式（10）～式（13）计算得到各评估指标的权重区间：

通过式（15）分别计算出各联系度确定性区间与不确定区间的相对权重：

最后根据式（16）计算得到评估指标“技能和经验u11”、“安全意识u12”、“注意力与警觉性u13”、“健康与疲劳u14”、“社会/家庭关系u15”的权重精确值：

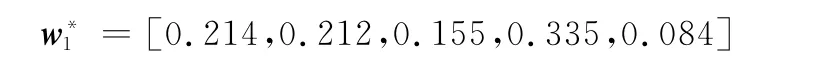
同理，根据评估人员对表1中其他各级风险指标的打分结果，按照以上步骤计算得到一级指标与其他二级指标的权重值：

3.2 评估风险态势以及趋势

针对该维修基地的实际状况，邀请10位航空维修专家到该维修基地进行实地考察和信息收集，根据五级风险评语集进行风险等级评判，得到打分结果R，并结合已求出的各评估指标权重，通过式（17）得到风险的同异反评估模型。根据式（5）～式（8）以及趋势评判原则，利用Matlab计算五元联系数的各阶偏联系数，结果如表3和表4所示。

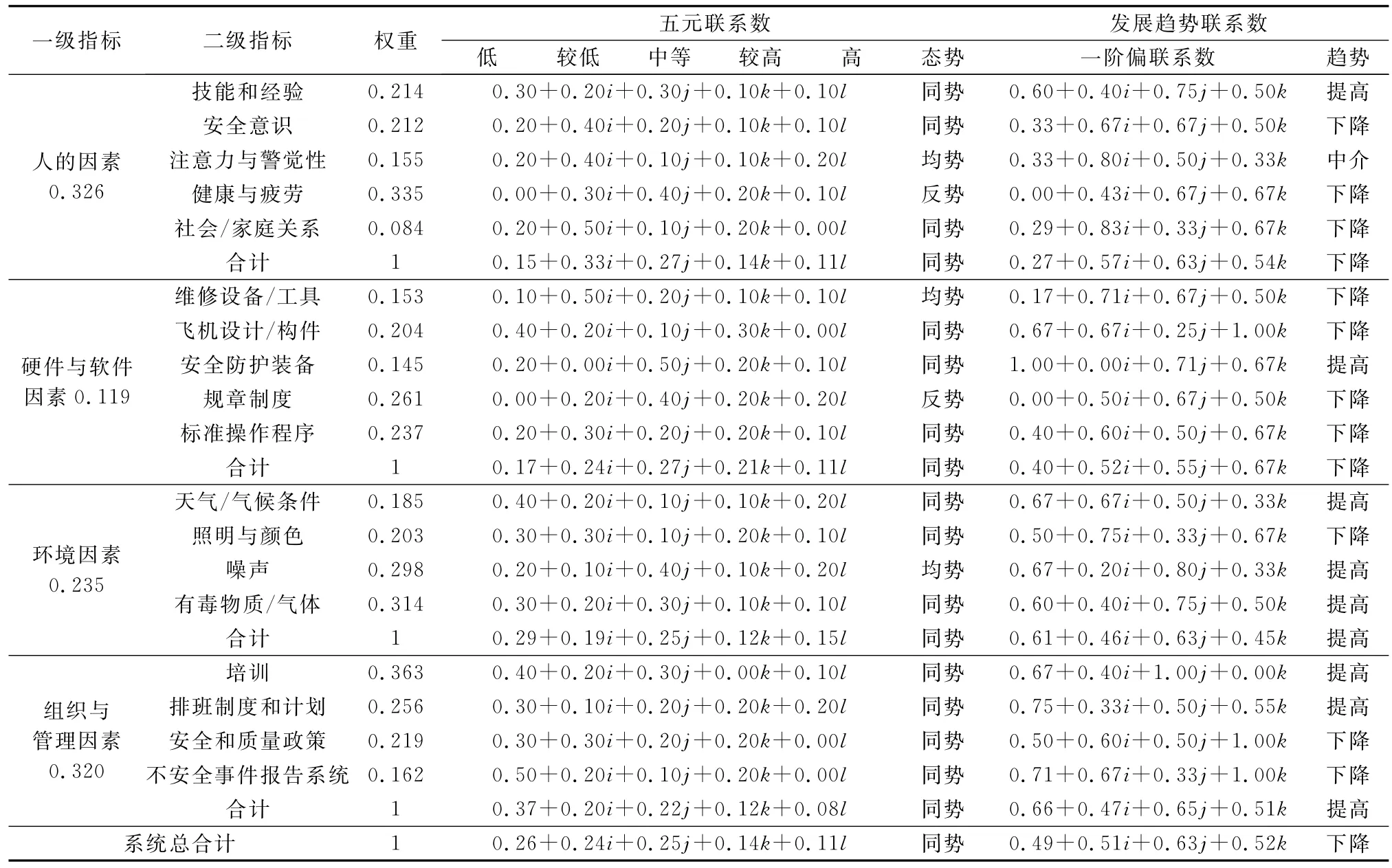
表3 风险联系数及计算表

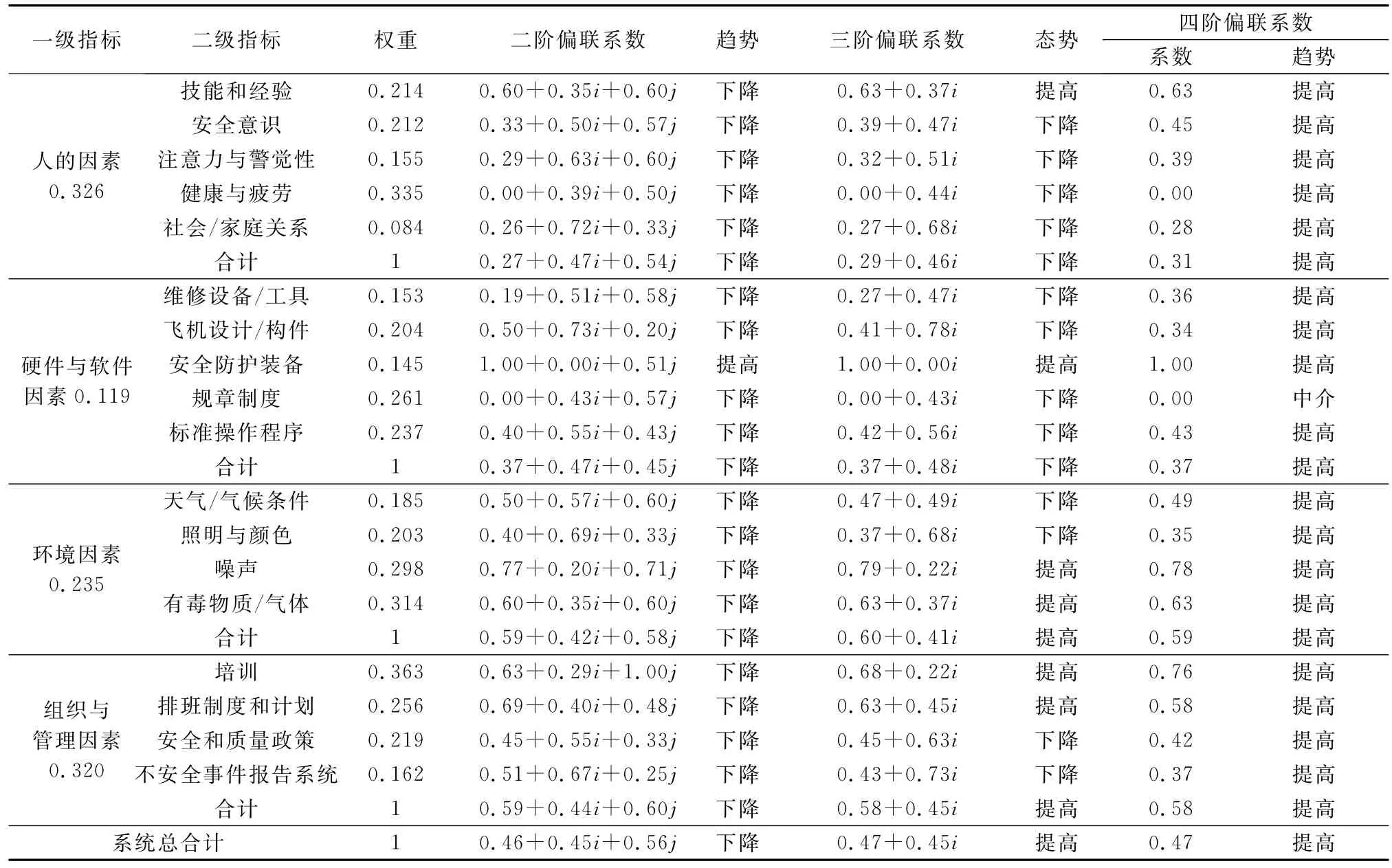
表4 风险联系数及计算表

根据表3中五元联系数的联系分量a、b、c、d、e的大小关系查询五元联系数态势排序表，一级评估指标“人的因素u1”、“硬件与软件因素u2”、“环境因素u3”、“环境因素u3”、“组织与管理因素u4”以及维修系统总风险的态势结果分别如下：

μ（u1）=0.15+0.33i+0.27j+0.14k+0.11l：a＞e，a ＜b，b＞c，c＞d，d＞e，同势47级；μ（u2）=0.17+0.24i+ 0.27j+0.21k+0.11l：a＞e，a＜b，b＜c，c＞d，d＞e，同势61级；μ（u3）=0.29+0.19i+0.25j+0.12k+0.15l：a＞e，a＞b，b＜c，c＞d，d＜e，同势21级；μ（u4）=0.37+0.20i+ 0.22j+0.12k+0.08l：a＞e，a＞b，b＜c，c＞d，d＞e，同势19级；μ（u）=0.26+0.24i+0.25j+0.14k+0.11l：a＞e，a＞b，b＜c，c＞d，d＞e，同势19级。

结果显示，该维修系统的总体风险态势处于同势19级，而且属于强同势区，表明系统处于低风险状态。一级指标中，“人的因素u1”和“硬件与软件因素u2”分别为同势47级和同势61级，均为微同势，表明状况一般，应稍加关注，对其下属二级指标中处于“均势”和“反势”的指标应重点关注，尤其是“健康与疲劳”和“规章制度”；“环境因素u3”和“组织与管理因素u4”分别为同势21级和同势19级，均为强同势，表明状况较好。

此外，从该维修系统的总体风险发展趋势来看，在一阶和二阶潜在层次上呈现下降趋势，表明系统情况变差，风险不断增高；在三阶和四阶潜在层次上呈现提高趋势，表明系统情况转好，风险逐渐降低，反映了维修系统的风险态势客观上存在同中有反、反中有同、波动前行的发展趋势。从二级评估指标的发展趋势来看，应重点关注多次呈现下降趋势的因素，如“安全意识”、“健康与疲劳”、“社会/家庭关系”、“规章制度”、“标准操作程序”、“照明与颜色”和“安全和质量政策”等。

针对上述计算和分析结果，应提出具有预见性和有效性的防控措施：制定科学合理的排班制度和计划，保证维修人员的休息时间，避免维修人员因工作负荷过大而导致身体疲劳，维修人员适当参与文体活动，缓解身体疲劳和精神压力；完善安全政策和规章制度，通过培训提高维修人员的安全意识，强调班组合作与交叉互检，提高信息沟通的及时性和完整性，确保标准检修程序得到有效实施；定期对维修环境中的硬件条件进行校验，降低设备方面对维修工作产生的负面影响。从而防止或减少维修差错事件的发生，降低维修事故率，不断提高航空维修系统的安全水平。

4 结 论

本文将集对分析理论和不确定A H P法引入航空维修系统的风险态势评估以及趋势分析中，并利用实例进行计算和验证，得到以下结论：

利用不确定A H P法并考虑专家权重确定各评估指标的权重区间，符合专家决策思维和工程实践，通过三元联系数的表达形式将权重区间转化为权重精确值，使计算结果更加科学合理。

根据五元联系数的定义建立风险的同异反评估模型，利用其联系分量的大小关系计算出该维修系统的当前态势为同势19级，处于低风险状态，通过计算其各阶偏联系数表明该系统今后存在同中有反、反中有同、波动前行的发展趋势，并找出“安全意识”、“健康与疲劳”等薄弱环节，提出了针对性防控措施。

通过实例分析验证了多元联系数集对分析在航空维修系统风险评估中应用的可行性和有效性，实现了静态与动态分析的有效结合，形似模糊综合评价法，但其实质是基于集对理论，是对系统中模糊性、随机性、灰色性等不确定因素的辩证认识。该评估方法的数学模型简单易懂，物理意义明确，计算结果准确客观，可在其他类似系统的风险评估及趋势分析中加以推广应用。

［1］Civil Aviation A uthority.A n introduction to aircraft maintenance engineering hu man factorsfor JA R 66［R］.U K：Civi l Aviation Authority，2002.

［2］Jin C C，Zuo H F.Design and im plementation of airline’s maintenance quality management system［J］.Computer Integrated Manufacturing Systems，2013，19（12）：3107-3113.（金灿灿，左洪福.航空公司维修质量管理系统设计与实现［J］.计算机集成制造系统，2013，19（12）：3107-3113.）

［3］Yu X H.Research on aeronautical maintenance safety management based on risk management［D］.Shenyang：Shenyang Aerospace U niversity，2011.（于晓欢.基于风险管理的航空维修安全管理机制研究［D］.沈阳：沈阳航空航天大学，2011.）

［4］Li T，Jiang Y J，Sun Z Q，et al.Analysis of relationships between aviation maintenance error m odes and their causes based on grey relational analysis method［J］.China Safety Science Journal，2011，21（2）：85-89.（李涛，蒋英杰，孙志强，等.航空维修差错模式及差错成因的灰色关联分析［J］.中国安全科学学报，2011，21（2）：85-89.）

［5］Zhang X Q，Wang H.Determination of hu man error probability in aircraft maintenance based on entropy weight and H D T［J］. China Safety Science Journal，2012，22（1）：100-105.（张晓全，王欢.基于熵权-H D T的航空器维修人误概率确定［J］.中国安全科学学报，2012，22（1）：100-105.）

［6］Wang Y F.Security analysis and evaluation in civil aviation maintenance based on human factor［D］.Nanjing：Nanjing University of Aeronautics and Astronautics，2009.（王岩峰.基于人为因素的民航维修安全分析与评估研究［D］.南京：南京航空航天大学，2009.）

［7］Li T S，H e Q L.Application of set pair analysisin the risk evaluation of coal spontaneous combustion［J］.Journal of Safety Science and Technology，2013，9（8）：54-58.（李同锁，何启林.集对分析在煤炭自然发火危险性评价上的应用［J］.中国安全生产科学技术，2013，9（8）：54-58.）

［8］Li L B，Fu X S.Safety of evaluation ofintersection based on SP A［J］. Journal of Wuhan University of Technology（TransportationScience&Engineering），2013，37（3）：542-544.（李丽斌，符锌砂.基于集对分析的平面交叉口安全性评价［J］.武汉理工大学学报：交通科学与工程版，2013，37（3）：542-544.）

［9］Li W B，Yao A M.Application of five-element connection number in evaluation of ground water quality based on entropy［J］. Journal of Water Resources and Water Engineering，2013，24 （2）：118-120.（李文宾，姚阿漫.基于熵权的五元联系数在地下水水质评价中的应用［J］.水资源与水工程学报，2013，24 （2）：118-120.）

［10］H u X B，Yuan Z P，Xu Y.Research on evaluation of the maturity of learning organization building and development based on set pairs［J］.Operation Research and Management Science，2013（1）：126-131.（胡信布，袁治平，徐渝.基于集对分析的学习型组织建设成熟度评估研究［J］.运筹与管理，2013（1）：126-131.）

［11］Li C，Chen J H，Yang S，et al.Application of five-element connection number to comprehensive evaluation of risks involved with sub way construction［J］.China Safety Science Journal，2013，23（10）：21-26.（李聪，陈建宏，杨珊，等.五元联系数在地铁施工风险综合评价中的应用［J］.中国安全科学学报，2013，23（10）：21-26.）

［12］Marais K B，Robichaud MR.A nalysis of trends in aviation maintenance risk：an empirical approach［J］.Reliability Engineering&System Safety，2012，106（4）：104-118.

［13］Patankar M S，Taylor J C.Risk management and error reduction in aviation maintenance［M］.Aldershot：Ashgate，2004.

［14］Zhao K Q.Set pair analysis and its preliminary application［M］. Hangzhou：Zhejiang Science&Technology Press，2000.（赵克勤.集对分析及其初步应用［M］.杭州：浙江科学技术出版社，2000.）

［15］Zhao K Q.Application and basic principles of connection mathematics［J］.Journal of Anyang Institute of Technology，2009 （2）：107-110.（赵克勤.联系数学的基本原理与应用［J］.安阳工学院学报，2009（2）：107-110.）

［16］Zhou X H，Zhang J J.Risk comprehensive evaluation method and its application based on the five-element connection nu mber［J］. Systems Engineering-Theory&Practice，2013，33（8）：2169-2176.（周兴慧，张吉军.基于五元联系数的风险综合评价方法及其应用［J］.系统工程理论与实践，2013，33（8）：2169-2176.）

［17］W u T.Application on the analysis of developmental trend of the student mark with five-element partial connection number［J］. M athematicsin Practice and Theory，2009（5）：53-59.（吴亭.五元联系数在学生成绩发展趋势分析中的应用［J］.数学的实践与认识，2009（5）：53-59.）

［18］Zhang X Q，Pan J，Wang H，et al.Analysis of fatigue causes for aircraftmaintenance personnel［J］.China Safety Science Journal，2013，23（2）：97-102.（张晓全，潘晶，王欢，等.机务人员疲劳致因影响分析［J］.中国安全科学学报，2013，23（2）：97-102.）

［19］Shyur H J.A quantitative model for aviation safety risk assessment［J］.Computers&Industrial Engineering，2008，54（1）：34-44.

［20］Cheng F，Luo J.Improved uncertain type of A H Palgorith ms［J］. Journal of Xiamen University（Natural Science），2006，45（2）：186-190.（程菲，罗键.一种改进不确定型A H P算法探讨［J］.厦门大学学报：自然科学版，2006，45（2）：186-190.）

［21］Yu S P，Li SM.Security risk assessment of tunnel design based on set pair analysis［J］.Journal of Chongqing Jiaotong University（N atural Science），2014，33（4）：38-43.（俞素平，李素梅.基于集对分析的隧道设计安全风险评估研究［J］.重庆交通大学学报（自然科学版），2014，33（4）：38-43.）

［22］Wang G P，Yang J，Wang HG.Application of five-element connection number to the quality assessment of the surface water environment［J］.Journal of Safety and Environment，2006，6（6）：21-24.（王国平，杨洁，王洪光.五元联系数在地表水环境质量评价中的应用［J］.安全与环境学报，2006，6 （6）：21-24.）

Risk state evaluation of aviation maintenance based on multiple connection number set pair analysis

S HI Zhi-jian，W A N G Hua-wei，WANG Xiang
（College of Civil Aviation，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，China）

In order to enhance the effectiveness of risk evaluation of the aviation maintenance system，multiple connection number theory set pair analysisis proposed，and certain indicators and uncertain indicatorsin the evaluation system are regarded as a whole.Firstly，the uncertain analytic hierarchy process is introduced to determine the weightinterval of evaluation indicators，in which the intervaljudgment matrix is constructed and expert weight is considered.According to the connection degree expression of three-element connection number，the weight interval of evaluation indicators is converted into the precise weight.Secondly，the uncertain item of three-element connection number is expanded to five-element connection number，and the same-indefinite-contrary modelis constructed to assess system risk.Finally，the set pair potential is calculated to judge the risk state of the system.Utilizing the partialconnection number，the risk develop menttrend is analysed，which realizes effective combination of static and dynamic evaluation.Through the case study of a maintenance base of airline，the analysis results indicate the adopted method is feasible and effective.

aviation maintenance；set pair analysis；multiple connection number；risk evaluation

X 913.4

A

10.3969/j.issn.1001-506 X.2016.03.18

1001-506 X（2016）03-0588-07

2015-01-07；

2015-09-05；网络优先出版日期：2015-12-14。

网络优先出版地址：http：∥w w w.cnki.net/kcms/detail/11.2422.T N.20151214.1345.004.html

国家自然科学基金和中国民航局联合基金（U1233115）；国家自然科学基金（71401073）资助课题

施志坚（1990-），男，硕士研究生，主要研究方向为民航系统安全性分析、风险评估。

E-mail：shizhijian1307012@163.com

王华伟（1974-），女，教授，博士后，主要研究方向为复杂系统可靠性分析与建模研究。

E-mail：huawei@nuaa.edu.cn

王 祥（1991-），男，硕士研究生，主要研究方向为民航安全工程、航空器适航管理。

E-mail：1207045336@qq.com