网络控制系统的事件触发与量化控制协同设计

马巧利，周 川，陈兰浪（南京理工大学自动化学院，江苏　南京210094）

网络控制系统的事件触发与量化控制协同设计

马巧利，周 川，陈兰浪
（南京理工大学自动化学院，江苏南京210094）

针对资源受限的离散时间网络控制系统，提出一种基于性能优化的事件触发和量化控制协同设计方法。该方法主要通过事件触发降低网络带宽占用，采用带有缩放因子的动态量化器降低量化误差的影响，并将该网络控制系统建模成具有不确定参数的离散时间切换系统；根据稳定性和二次性能指标要求，利用分段李雅普诺夫函数和线性矩阵不等式技术将性能指标最优问题转化为具有矩阵不等式约束的优化问题，给出了保证系统渐近稳定且二次性能指标最小的事件触发器参数、动态量化器可调参数及控制器增益协同设计方法。最后，通过仿真验证了所提方法的有效性。

网络控制系统；事件触发器；量化控制；二次性能指标；协同设计

网址：www.sys-ele.com

0 引 言

网络控制系统（networked control system，N CS）因具有易扩展、成本低、连接线少等诸多优点，得到了深入的研究与广泛应用。然而，网络控制系统也存在着数据丢包、延时、带宽受限等问题，从而影响到控制系统的性能。针对带宽受限问题，通过引入事件触发机制减少信息传输次数，可降低带宽占用以提高网络服务性能。因而，事件触发机制的设计成为解决网络控资源受限问题的重要途径之一。

事件触发机制因其“按需传输”的特性，在带宽受限的网络控制系统中得到广泛研究［1-7］。文献［1］针对具有通信时延和数据丢包的网络控制系统，给出了非理想通信条件下保证系统渐近稳定的事件触发机制和H∞控制器协同设计的方法。文献［2-4］针对网络控制系统中状态不完全可测情况，研究了基于事件触发的输出反馈控制问题。文献［5-6］针对带有扰动的网络控制系统，分别设计了使系统有界稳定的事件触发条件和使系统指数稳定并具有H∞性能指标的事件触发条件和控制器增益。文献［7］针对一类连续时间非线性系统，基于系统状态和最优预测状态间的误差，给出了保证系统有界稳定的事件触发模型预测控制算法。该算法通过降低优化问题的求解频率节约了计算资源。文献［8］针对分布式事件触发控制系统，针对每个传感器单独设计事件触发条件，并利用启发式算法实现了事件触发参数的在线自适应调整。针对网络控制系统的性能优化问题，文献［9］基于二次性能指标最优研究了保证系统渐近稳定和二次性能指标最小的调度器和控制器的协同设计方法。然而，网络控制系统作为一类离散数字控制系统通常要采用量化器及量化控制，上述研究结果未考虑网络控制系统的量化问题。针对网络控制系统中的量化问题，文献［10-12］采用静态量化器，给出了保证系统渐近稳定的事件触发条件和控制器增益协同设计方法。为了减小静态量化器的量化误差，带有动态量化器的量化控制问题得到了广泛研究。文献［13］提出了一种在线更新量化器参数的控制策略，并使系统具有H∞性能指标。文献［14-15］分别针对线性、非线性系统研究了时变量化器作用下的的量化控制问题，通过调整量化误差界使得系统全局渐近稳定。针对另一种由静态量化器和缩放因子联合构成的动态量化器，文献［16］研究了线性系统的量化输出控制问题，联合设计了使系统稳定动的态量化器和输出反馈控制器。文献［17］针对一类带有非线性干扰的线性系统的量化反馈问题，通过改造水平-中心型均匀量化器设计了使量化误差指数趋于零的量化策略，并给出了保证系统输入-状态稳定（input-to-state stability，ISS）稳定的充分条件。以上研究仅单一考虑了保证系统渐近稳定的触发机制或量化器的设计及量化控制问题。为进一步提高网络控制系统的综合性能，降低设计的保守性，本文将在已有的研究基础上寻求使得系统渐近稳定并具有最小二次性能指标的触发器、动态量化器和控制器协同设计方法。

本文主要工作和贡献是针对一类资源受限的离散时间网络控制系统，提出一种基于性能优化的事件触发机制和量化控制协同设计方法。该方法通过事件触发来降低网络带宽占用并用动态量化器减少量化误差，建立网络控制系统的离散时间切换系统模型，利用分段李雅普诺夫函数和线性矩阵不等式（linear matrix inequality，L MI）技术，给出使系统渐近稳定并具有最小二次性能指标的事件触发参数、控制器增益和动态量化器参数的协同设计策略。

1 问题描述

考虑一类离散时间线性时不变网络控制系统：

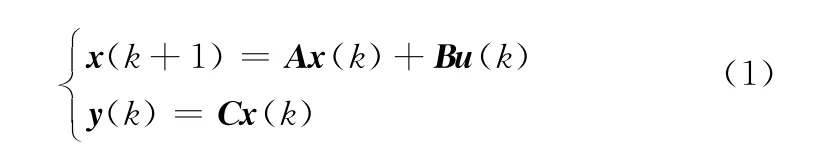
式中，x（k）∈Rn，u（k）∈Rm，y（k）∈Rn分别为被控对象的状态变量、控制输入、输出变量；A，B，C均为适维矩阵。

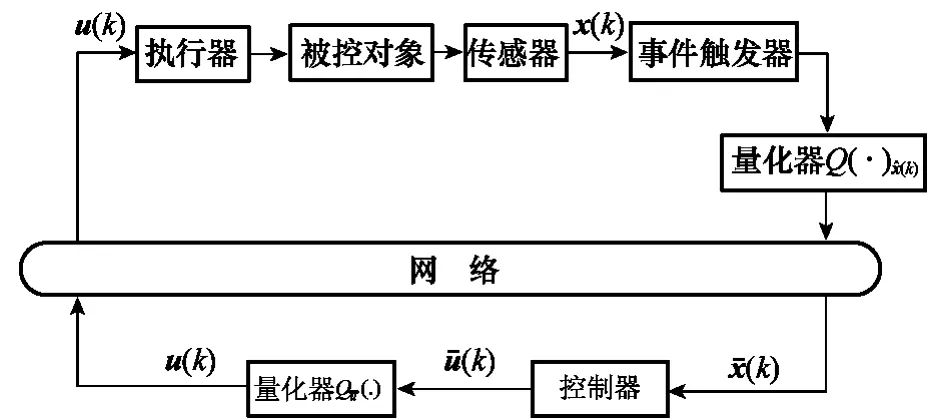
图1 网络控制系统结构

假设1 传感器为时间驱动，采样周期为h，控制器和执行器均为事件驱动，且数据传输采用单包传输。

网络控制系统的结构如图1所示，系统在每个采样时刻的采样状态记为x（k）（k=0，1，2，…）。事件触发器根据触发条件判断该采样状态是否需要经网络传输。（k）表示k时刻经过触发器之后的传输状态，（k）表示经过量化器（·）作用后的状态信息。（k）和u（k）分别表示经过量化器（·）前后的控制输入。

事件触发条件设计如下：

式中，＾x（k-1）表示最近一次传输的状态，当系统当前状态x（k）满足触发条件（2）时更新传输的状态信息。σ是根据二次性能指标（5）确定的最优阈值参数。记

则有

选取如下二次性能指标：

式中，Q=diag｛Q1，Q2｝∈R（n+m）×（n+m），Q1∈Rn×n，Q2∈Rm×m均为正定矩阵。

且具有如下性质：

动态量化器可表示为

因此，动态量化器的量化范围和量化误差界分别为Mμ 和Δμ。根据量化器的输入值v在每个采样时刻对μ进行调整。具体调整方法分为两个阶段：当初始状态未知时，增加μ直到v能够被测量到，即v位于量化范围之内，此时，v的值将迅速下降到趋于0的邻域；当v在0的邻域时，减少μ，使v收敛至平衡点。通过不断调整缩放因子μ的大小，减少量化误差对系统的影响，并使网络控制系统最终渐近稳定。当v∈Rn，即v为向量时，Q（v）=（Q（v1），Q（v2），…，Q（vn））。

采用如下控制器：

式中，K为控制器增益。根据式（9），经量化器作用有

令η（k）=（xT（k）（k-1））T，则由式（1）、式（4）、式（10）～式（12）得闭环网络控制系统状态方程为

式中

本文研究目标是针对闭环网络控制系统（13），设计事件触发条件（2）的阈值参数、控制器增益（10）以及动态量化器的调整策略式（11）、式（12），使得系统渐近稳定并满足二次性能指标（5）最小。即

2 基于二次性能的事件触发机制和量化控制协同设计

引理1［18］给定对称矩阵，其中S11是 r×r的矩阵，则以下3个不等式是等价的：

引理2［19］对于任意适当维矩阵X，Y和任意常数ε＞0，下列矩阵不等式成立：

定理1 针对闭环网络控制系统（13），采用事件触发机制（2）、量化器（11）、（12）和控制器（10），若存在正定矩阵P0∈R2n×2n，P1∈R2n×2n，Q∈R（m+n）×（m+n），常数0＜σ＜1，量化器的缩放因子μ1k，μ2k，使得Pα（k+1）=P0，P1时，式（15）成立，则闭环网络控制系统（13）渐近稳定且二次性能指标（14）的上界最小。

其中

证明 （1）引入分段二次李雅普诺夫函数：

式中，η（k）=（xT（k）（k-1））T；Pα（k）∈R2n×2n为对称正定矩阵。

如果对任意η（k）≠0，ΔV（k）满足

式中，tr（·）表示矩阵的迹，根据

因此式（19）等价于最小化性能指标式（14）的上界，即式（15a）。

（2）稳定性条件：

根据式（4）、式（11）、式（12）有

记

下面针对不同状态下的α（k）讨论系统的渐近稳定性：

（1）α（k）=0时，即k时刻未触发，根据事件触发条件（2）有：eT（k）e（k）＜σxT（k）x（k），假设k+1时刻的触发状态未知，则

由量化器的缩放因子调节规律式（15d）和式（15e），存在一个ε∈（0，1）使得下式成立：

根据量化器性质（7），当|＾x（k）|≤M1μ1k，|¯u（k）|≤M2μ2k时，有

由式（15b）与式（23）知

即式（17）成立。

（2）同理，当α（k）=1，即k时刻触发时，根据事件触发条件（2）有：eT（k）e（k）≥σxT（k）x（k），假设k+1时刻的触发状态未知，令

根据式（15c）知Φ1＜0，有

J′＜-ε2λmin（-Φ1）|η（k）|2＜0，即式（17）成立。综上可知，闭环网络控制系统（13）渐近稳定。证毕

下面定理2是将定理1转化为具有线性矩阵不等式约束的优化问题。

定理2 针对闭环网络控制系统（13），采用事件触发机制（2）、动态量化器（11）（12）和控制器（10），若存在正定矩阵P0∈R2n×2n，P1∈R2n×2n，Y ∈R（m+n）×（m+n），以及常数0＜σ＜1，矩阵K，量化器缩放因子μ1k，μ2k，使得Pα（k+1）=P0，P1时式（24）成立，则闭环网络控制系统（13）渐近稳定且二次性能指标（14）的上界（19）最小。即定理1的优化问题转化为以下L MI优化问题：

式中

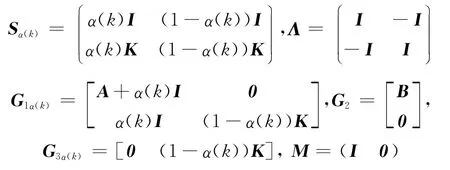
证明 由引理1，式（15b）可转化为

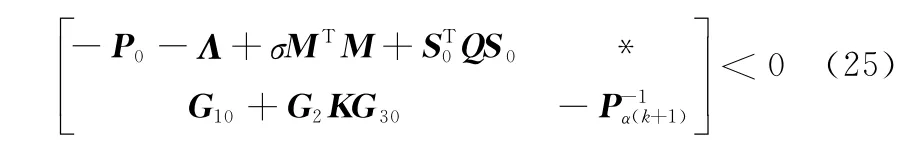
再次利用引理1，式（25）可转化为

式（26）分别左乘、右乘diag｛I，Pα（k+1），I｝，有

由引理2，分离Pα（k+1）、K得

由引理1，式（28）可转化为

令Y=Q-1，可得式（24b）。

同理，式（15c）可转化为

令Y=Q-1，可得式（24c）。综上可知定理2成立。证毕

3 算例仿真

考虑N CS中被控对象离散时间状态方程如下：

根据定理2，利用L MI工具箱求得

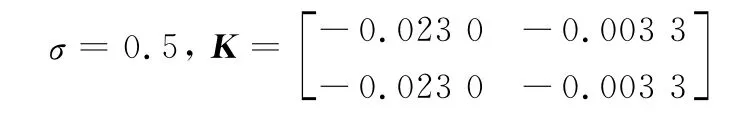
不同的触发状态下对应的量化器参数范围如下：

设定系统的采样周期为0.1 s，初始状态为x（0）=［-6 6］T，量化器缩放因子分别取μ1k=0.3，μ2k=4.6。基于上述事件触发机制和量化控制的闭环网络控制系统的触发时刻及状态响应曲线如图2和图3所示，表1给出了事件触发阈值取不同值时对应的二次性能指标。

图2 事件触发时刻和触发间隔

表1 不同事件触发阈值对应的二次性能指标

图3 系统状态响应

由图2和图3仿真结果可知，本文所设计的事件触发机制和量化控制策略，可以明显减少触发次数并保证该闭环网络控制系统的渐近稳定性。表1表明，本文设计方法在不明显占用额外带宽的情况下可使二次性能指标最小。因此，上述基于二次性能指标的事件触发机制和量化控制协同设计策略，不仅减少了带宽占用且保证了闭环网络控制系统的渐近稳定性和二次性能指标最小。

4 结 论

本文主要针对一类资源受限的离散网络控制系统，研究了使系统渐近稳定且二次性能指标最小的事件触发器和控制器的协同设计方法。文中采用带有缩放因子的动态量化器，根据量化特性和事件触发机制将系统建模成具有不确定参数的离散时间切换系统；根据分段李雅普诺夫函数和线性矩阵不等式技术将性能指标最优问题转化为具有线性矩阵不等式约束的优化问题，并给出了最优事件触发参数、控制器增益和量化器的参数调整范围。最后，通过仿真，验证了该设计方法可以在减少带宽占用的同时保证系统渐近稳定且二次性能指标最小。本文后续工作将进一步研究实现事件触发参数的自适应在线动态调整方法。

［1］Peng C，Yang T C.Event-triggered co m m unication andH∞control co-design for networked control systems［J］.A utom atica，2013，49（5）：1326-1332.

［2］Zhang X M，H an Q L.Event-triggered dyna mic output feedback control for networked control systems［J］.IE T Control Theory and A pplications，2014，8（4）：226-234.

［3］Zhang J H，Feng G.Event-driven observer-based output feedback control for linear systems［J］.A utom atica，2014，50（7）：1852-1859.

［4］Y u H，Panos A.Event-triggered output feedback control for networked control systems using passivity：L2stability in the presence of co m m unication delays and signal quantization［J］. Automatica，2013，49（1）：30-38.

［5］Jan L，Daniel L.A state-feedback approach to event-based control［J］.Automatica，2011，46（1）：211-215.

［6］Yue D，Tian E G，Han Q L.A delay system method for designing event-triggered control lers of networked control systems［J］.IE E E Trans.on automatic control，2013，58（2）：475-481.

［7］Li H P，Shi Y.Event-triggered robust m odel predictive control of continuous-time nonlinear systems［J］.Automatica，2014，50 （5）：1507-1513.

［8］M anuel M J，Paulo T.Decentralized event-triggered control over wireless sensor/actuator networks［J］.IE E E Trans.on Automatic Control，2011，56（10）：2456-2461.

［9］Sanad A，Daniel G，Steven L.Event-based networked control and scheduling codesign with guaranteed performance［J］.Automatica，2015，57：128-134.

［10］H u S L，Y ue D.Event-triggered control design of linear networked control systems with quantizations［J］.IS A Transactions，2012，51（1）：153-162.

［11］Yan H C，Yan S，Zhang H，et al.L2control design of eventtriggered networked control systems with quantizations［J］. Journal of the Franklin Institute，2015，325（1）：332-345.

［12］Qu F L，Guan Z H，He D X，et al.Event-triggered controlfor networked control systems with quantization and packet losses［J］. Journalof the Franklin Institute，2014，352（3）：974-986.

［13］Niu Y G，Daniel W.Control strategy with adaptive quantizer’s parameters under digitalco m m unication channels［J］.A utom atica，2014，50（10）：2665-2671.

［14］Brockett R，Liberzon D.Q uantized feedback stabilization of linear systems［J］.IE E E Transactions on A utomatic Control，2000，45（7）：1279-1289.

［15］Liberzon.H ybrid feedback stabilization of systems with quantized signals［J］.Automatica，2003，39（9）：1543-1554.

［16］Fu M Y，Xie L H.Finite-level quantized feedback control for linear systems［J］.IE E E Trans.on A utom atic Control，2009，54（5）：1165-1170.

［17］Liu W，W ang Z M，Ni MK.Q uantized feedback stabilization for a class of linear systems with nonlinear disturbances［J］. N onlinear Analysis：H ybrid Systems，2013，54（8）：48-56.

［18］Ji Z，W ang L，Xie G，et al.Linear matrix inequal ity approach to quadratic stabi l ization of switched systems［J］.IE E Proceedings-Control Theory and Applications，2004，151（3）：289-294.

［19］Barmish B R.Necessary and sufficient conditions for quadratic stabi l ity of an uncertain system［J］.Journal of Optimization Theory and Applications and Applications，1985，46（4）：399-408.

Co-design of event-trigger and quantized control for networked control systems

Ma Qiao-li，Zhou Chuan，Chen Lan-lang
（School of Automation，Nanjing University of Science and Technology，Nanjing 210094，China）

A co-design scheme of event-triggered mechanism and quantized control based on optimal performance for a class of discrete-time networked control system（N CS）with resource constrained is proposed. The proposed method can reduce the occupation of network bandwidth by event-triggered mechanism and also reduce the quantized error by using dynamic quantizer with adjustable zoo ming parameters，then the N CS is modeled as a discrete-time switched system with uncertain parameters.Furtherm ore，based on the requirement of stability and quadratic performance index，the design problem is converted into an optimization problem with linear matrix inequality（L MI）constraints by using piecewise Lyapunov function and L MI techniques，and the co-design method of corresponding event-trigger parameter，the adjustable parameter of dynamic quantizer and controller gain is provided to ensure asymptotic stability and minim u m quadratic performanceindex.Finally，we verify the effective of the proposed scheme by simulation.

networked controlsystems；event-trigger；quantized control；quadratic performanceindex；co-design

T P 13

A

10.3969/j.issn.1001-506 X.2016.03.27

1001-506 X（2016）03-0652-06

2015-09-23；

2015-10-25；网络优先出版日期：2015-11-23。

网络优先出版地址：http：∥w w w.cnki.net/kcms/detail/11.2422.T N.20151123.1324.010.html

南京理工大学研究生创新计划项目（NJU S T GIP201408）资助课题

马巧利（1990-），女，硕士研究生，主要研究方向为网络控制系统的调度与控制。

E-mail：maqiaoli11@163.com

周 川（1970-），男，博士、教授，主要研究方向为系统的故障诊断与重构控制、网络控制系统的分析与设计。

E-mail：njust_zc@126.com

陈兰浪（1994-），男，主要研究方向为网络控制系统。

E-mail：chenlanlang2015cll@163.com