串联增强型电磁轨道炮螺栓预紧封装性能分析
石江波,栗保明
(南京理工大学 瞬态物理国家重点实验室,江苏 南京 210094)
串联增强型电磁轨道炮螺栓预紧封装性能分析
石江波,栗保明
(南京理工大学 瞬态物理国家重点实验室,江苏 南京210094)
为了研究螺栓连接预紧方式的串联增强型轨道炮的身管封装性能,从电磁场的角度出发,计算了电磁轨道炮发射时导轨中的电磁力,进而得到了身管应力、应变和位移量。建立三维串联增强型电磁轨道炮离散预紧身管模型,计算了在一种斜坡电流激励条件下导轨的应力、应变和位移量的变化规律,以及身管封装部件应力、应变及位移的变化规律。从计算结果看出,在螺栓预紧条件下,导轨及身管处于一定初始位移及应力、应变下,随着电流的逐渐增大和作用时间增大,各参量也逐渐增大,且呈现明显的波动状,导轨的位移在螺栓位置有明显的下降趋势。身管部件的最大位移量远小于导轨的位移量,保证了与导轨的接触,也在一定程度上控制了导轨的最大位移量,对身管的封装性能有积极的作用。
串联增强;电磁轨道炮;离散封装;螺栓预紧;封装性能
电磁发射技术作为一项可行性较强的未来武器技术引起了世界上许多军事强国的关注,各国都在进行这方面的研究[1-8]。目前,美国在海军、陆军的支持下,理论和应用研究都处于领先地位[3-4,8]。为了获得更高的弹丸初速和发射效率,各国学者对电枢的性能[7-9]、导轨结构[10]、电枢与导轨的适应性[6-9]、电枢与导轨的接触条件[7-8,11-12]以及电源与发射系统的匹配性[13]等方面做了大量研究。而身管的绝缘封装性能也是影响发射的一个重要因素。若发射过程中电枢与导轨出现缝隙,会产生电弧烧蚀导轨或电枢;身管部件间出现缝隙,轻则烧蚀绝缘材料,影响发射装置的绝缘性能,重则影响身管寿命与发射试验的安全可靠。
螺栓连接离散预紧方式便于拆装,预紧力容易施加,成为目前阶段试验研究的主要身管封装方式[14-16]。笔者建立螺栓连接离散预紧方式串联增强性电磁轨道炮身管模型,给出了一种导轨电磁力的计算方法,进而分析离散预紧方式下身管的应力、应变及位移。计算了在兆安级电流激励条件下导轨及身管应力、应变和位移的变化规律,分析离散预紧身管的封装性能。
1 导轨电磁力计算方法
电磁轨道炮身管在发射时主要受到导轨的电磁力和电枢对导轨的作用力以及身管的预紧力的影响,而电枢对导轨的作用力仅作用在电枢所在位置处,其余位置不受影响,对身管整体分析,可忽略电枢对导轨的作用力,仅考虑导轨中的电磁力作用。导轨中的电磁力计算模型如图1所示。
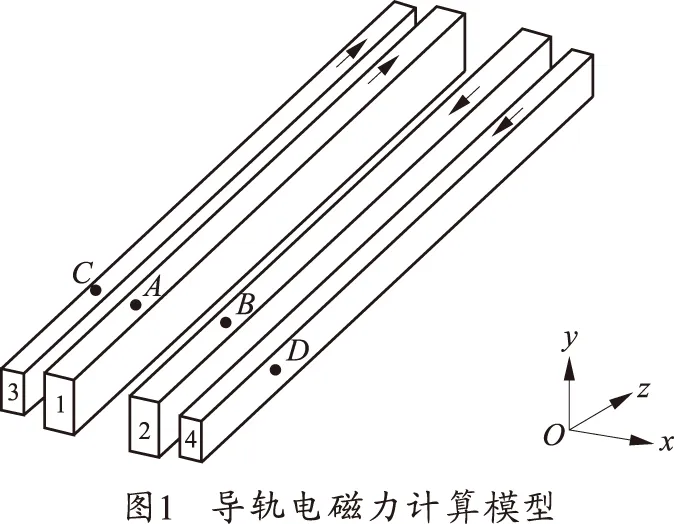
导轨1~4上分别有点A(x1,y1,z1),B(x,y,z),C(x2,y2,z2),D(x3,y3,z3)。导轨1和3中电流方向相同;导轨2和4中电流方向相同,且与导轨1、3中电流方向相反,如图1导轨中箭头所示。
假设一侧导轨1上A点处有电流元I1dl1,I1为电流大小,l1为电流元的方向矢量,在另一侧导轨2上B点处产生的磁感应强度为
(1)
式中:B1为磁感应强度;μ0为真空磁导率;RAB为AB的位置向量,可表示为
RAB=(x-x1)i+(y-y1)j+(z-z1)k
其中i,j,k为沿x,y,z坐标轴的单位向量,且
RAB=[(x-x1)2+(y-y1)2+(z-z1)2]1/2
而I1dl1=I1dzk,于是式(1)可表示为
(2)
则导轨1在B点产生的磁感应强度即为整个导轨上各电流元在B点产生的磁感应强度的和,用积分形式可表示为
(3)
式中,dV为体积积分单元。
假设B点出有一电流元I2dl2,则B处的电流元方向应与A处电流方向相反,即可以表示为
I2dl2=-I2dzk
则该电流元在导轨1的电磁场作用下受到的电磁力为
(y-y1)j]dV=F1xi+F1yj
(4)
式中:F1x为沿x轴方向电磁力分量;F1y为沿y轴方向电磁力分量。
同理,得到B点处电流元受到导轨3的电磁力可以表示为
(y-y2)j]dV=F2xi+F2yj
(5)
式中:I3为导轨3上一点C(x2,y2,z2)处的电流元的电流大小;RCB=(x-x2)i+(y-y2)j+(z-z2)k,RCB=[(x-x2)2+(y-y2)2+(z-z2)2]1/2。
B点处电流元受到导轨4的电磁力可以表示为
(y-y3)j]dV=F3xi+F3yj
(6)
式中:I4为导轨4上一点D(x3,y3,z3)处的电流元的电流大小;RDB=(x-x3)i+(y-y3)j+(z-z3)k,RDB=[(x-x3)2+(y-y3)2+(z-z3)2]1/2。
导轨2上B点受到的电磁力的合力可以表示为
dF=dF1+dF2+dF3=F1xi+F1yj+F2xi+
F2yj+F3xi+F3yj=(F1x+F2x+F3x)i+
(F1y+F2y+F3y)j=Fxi+Fyj
(7)
根据求得到导轨中任一点的电磁力,可以建立导轨内任一点沿3个坐标轴方向的力学平衡方程
(8)
式中:σx,σy,σz分别为任一点沿坐标轴方向的正应力;τxy=τyx,τyz=τzy,τzx=τxz分别为任一点在3个坐标方向的剪切应力;Fx,Fy,Fz分别为单位体积的电磁力在x,y,z方向的分量。
身管其他部件则由力的传递关系得到相应位置的体积力,建立相应力学平衡方程。因此,从得到导轨各处的电磁力,即可应用材料力学相关知识求得身管各处的应力、应变情况。
2 身管模型
建立串联增强型轨道炮身管,采用螺栓连接封装方式,通过螺栓施加预紧力,身管整体呈现离散预紧状态。对身管模型进行如下简化:
1)考虑结构的对称性,并简化计算,建立1/4身管截面模型,身管长度为1m。
2)不考虑炮口、炮尾的主、副轨连接装置和炮尾的汇流装置,仅建立身管段的模型。
3)身管各部件间均为摩擦接触。
螺栓连接离散预紧身管截面及尺寸如图2所示,身管模型如图3所示。
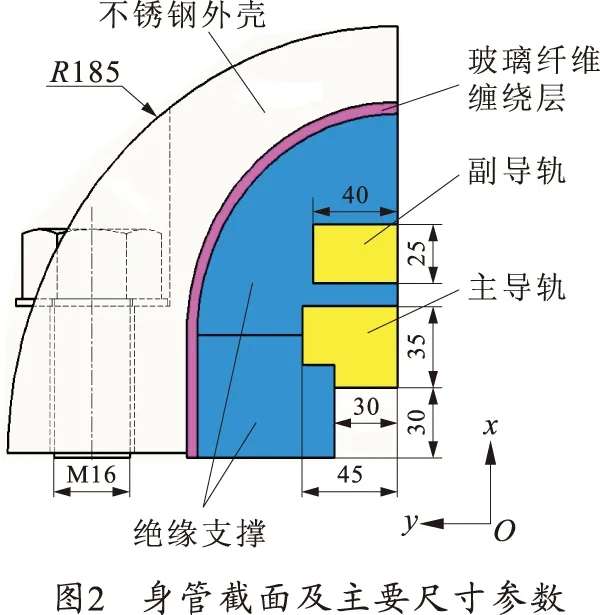

材料参数如表1所示。
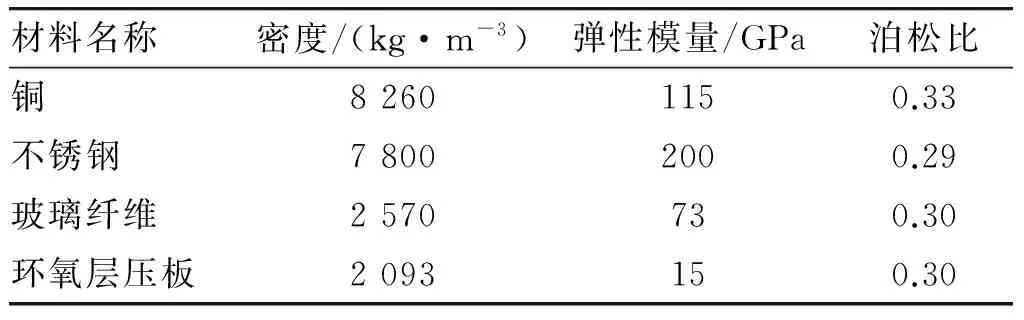
表1 材料参数
导轨中施加的电流激励按照图4所示的规律变化。
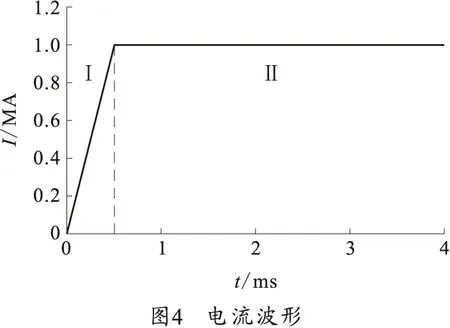
将电流分为3个阶段:电流0时刻,身管无电流作用;阶段Ⅰ:电流上升阶段,0-0.5 ms;阶段Ⅱ:电流峰值阶段,0.5-4 ms。
在身管对称面上施加对称约束;在身管一端施加x方向位移约束,约束身管在电枢运动方向上位移。身管预紧力通过螺栓施加,在计算过程时,通过施加螺栓预紧调整量实现预紧作用,在本文的计算中,螺栓调整量为1 mm。
3 结果分析与讨论
根据上述模型及激励条件,计算得到身管的应力、应变及位移情况,进而得到身管的封装性能。由于主导轨与电枢接触,且应力、应变和在y方向的位移量比副导轨大很多,因此以主导轨的计算结果作为分析对象。
3.1主导轨的位移
电流激励下主导轨上不同位置处的位移量随时间变化曲线如图5所示。
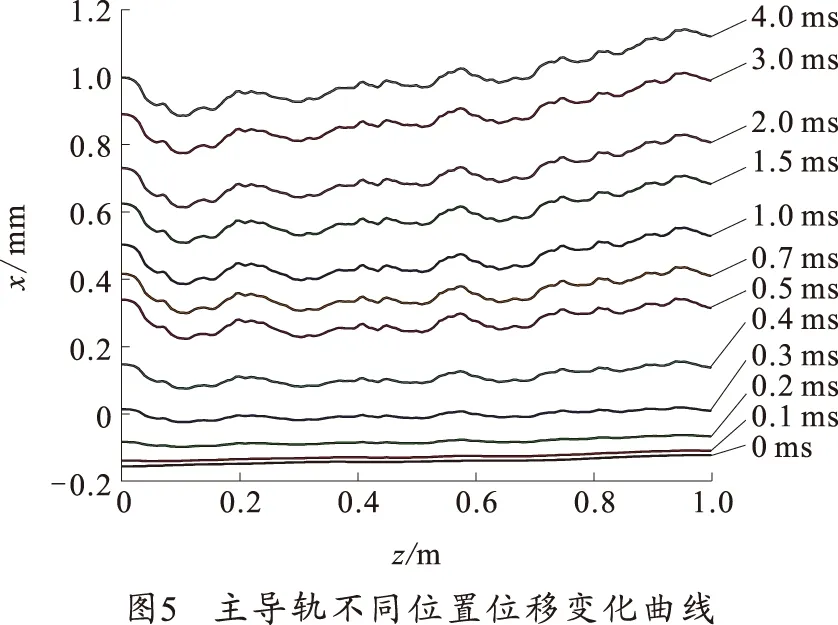
分成3个阶段讨论主导轨在电流作用下y方向的位移变化:
1)电流0时刻:电流为0,主导轨没有电磁力的作用,在螺栓的初始预紧力的作用下,主导轨y反向的位移量为负值,且整个主导轨的位移量均匀一致,约为-0.138 897 6 mm,说明在通过螺栓施加一定的预紧力后,身管的整体受力均匀一致。
2)阶段Ⅰ:随着电流的增大,主导轨的位移量逐渐增大,且在不同位置处出现了一定程度的差异。随着电流持续作用,主导轨各处y方向的位移量差异逐渐增大,在螺栓位置处主导轨的位移量较小,而在其他位置处的位移量则较大。在0.5 ms时刻,即当电流达到峰值时,主导轨y方向的位移量呈现有明显起伏趋势的“波浪”状。受螺栓与端面距离不同的影响,主导轨最大y方向位移出现在距离螺栓较远的一端,约为0.339 32 mm,而y方向最小位移出现在螺栓处,约为0.224 22 mm。
3)阶段Ⅱ:在该阶段内,主导轨的位移量仍继续增大,且波动更为明显。在螺栓位置处,主导轨y方向的位移量较小,出现“波谷”;而在螺栓之间主导轨的位移量较大,呈现“波峰”状。在4 ms时刻,主导轨y方向最大位移量约为1.119 6 mm,而y方向最小位移量为0.998 47 mm,与0.5 ms时刻相比,电流没有增大,但主导轨y方向位移量增大很多。
因此,为了使身管的受力均匀,采用螺栓连接方式时,需要注意螺栓的间距,尽量采用小间距、均匀分布的螺栓排布方式。
3.2主导轨的应变
主导轨上不同位置处的应变随时间变化曲线如图6所示。
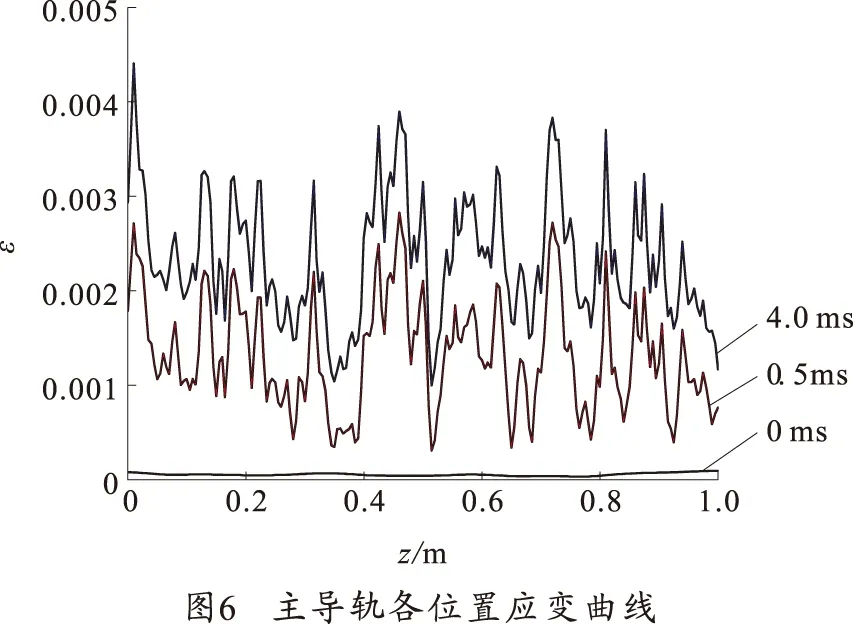
同样,将主导轨的应变分为3个阶段:电流初始阶段、电流上升阶段和电流峰值阶段。选取3个时刻(0、0.5和4.0 ms)来表征3个阶段主导轨的应变变化。
1)电流0时刻:由于电流较小,在螺栓的预紧力的作用下主导轨有一定的初始应变,约为5×10-5,且较为均匀,没有较大的波动。
2)阶段Ⅰ:在电流逐渐增大的过程中,随着电流持续增大,主导轨的应变也持续增大。同一位置处主导轨的应变随电流的增大而逐渐增大,电流达到峰值后仍以一定的速率增大。而主导轨上不同位置处的位移在同一时刻也出现较大的波动,主导轨的应变呈现振荡规律,出现“锯齿”状变化规律,主导轨的应变增大减小交替出现,在螺栓位置处,主导轨的应变有一定程度的增大,但在螺栓之间,主导轨的应变量也有增大和减小的变化。在身管两端,由于计算模型的约束条件限制,主导轨的应变较小,而在螺栓位置处,主导轨的应变则有一定程度的增大,这与螺栓的预紧力有关。因此,从螺栓段的导轨应变来看,主导轨的应变波动较大,且没有规律。主导轨的应变平均值为1.173 5×10-3,远大于主导轨初始时刻的应变。
3)阶段Ⅱ:在电流峰值阶段,主导轨中的电流与0.5 ms时刻大小一致,主导轨的应变变化规律与0.5 ms时刻基本一致,但由于电流持续作用,主导轨的应变值比0.5 ms时刻大,整个主导轨的应变平均值为2.335 6×10-3,较0.5 ms时刻增大约1倍。
3.3主导轨的应力
主导轨上不同位置处的应力随时间变化曲线如图7所示。

当主导轨材料未达到强度极限时,主导轨的应力是材料弹性模量与主导轨应变的乘积,即导轨的应力变化规律与主导轨的应变变化规律一致。
1)电流0时刻:由于螺栓预紧的作用,主导轨存在一定的初始应力,但应力较小,约为6 MPa,且较为均匀,没有明显的波动。主导轨上的最大应力出现在主导轨结构两平面相交的位置。
2)阶段Ⅰ:随着电流的逐渐增大和作用时间增加,主导轨的应力也逐渐增大,出现较大的波动;主导轨上同一位置处的应力随着电流作用时间的增加而增大,在电流上升阶段增大速率与电流上升速率成正比。主导轨上最大应力呈现点状分布。
3)阶段Ⅱ:电流维持在峰值电流,主导轨受到持续的电磁力作用,主导轨的应力也逐渐增大,主导轨上应力变化和分布规律与0.5 ms时刻基本一致。
3.4身管的应力、应变及位移
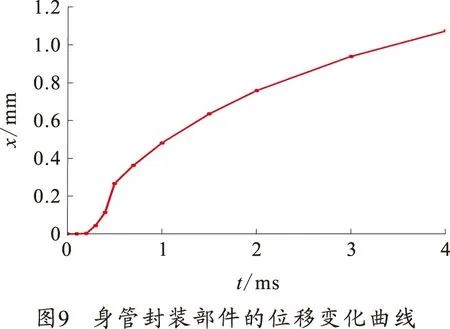
取身管封装部件在各时刻的最大应力、应变和位移量,得到各参量随时间变化曲线图,如图8、9所示。

如图8所示,身管部件的最大应力变化较大,且最大应力出现在螺栓连接位置处。在0时刻,身管由于螺栓的预紧作用,初始应力约为587.81 MPa;在0.5 ms时刻,最大应力增大至640.88 MPa;在4 ms时刻,身管部件的最大应力增大至1 038.6 MPa,远大于主导轨上的应力。而身管部件其他位置的应力则远远小于最大应力,处于较为安全的范围内。
由于螺栓连接位置的身管材料的刚度较大,因此最大应变与最大应力位置不同,最大应变出现在主导轨附近绝缘材料处。在电流上升阶段,该处的应变迅速增大,在0.5 ms时刻,最大应变从初始应变4.2×10-3增大到1.06×10-2;在4 ms时刻,身管最大应变增大至2.1×10-2,与主导轨应变相比,有很大程度的增大。
从图9可以看出,身管的最大位移也出现在导轨附近的绝缘材料处,从0时刻的负值初始位移逐渐增大,在0.5 ms时刻,位移值增大至0.265 mm;在4 ms时刻位移量为1.073 mm,均小于主导轨的位移量,说明绝缘材料仍与导轨保持接触,没有缝隙,满足身管的封装要求。
4 结束语
为了分析螺栓连接离散预紧方式下身管的封装性能,从理论的角度给出了导轨电磁力的计算方法和身管应力应变的计算方法。建立了离散预紧身管模型,计算了兆安级电流激励条件下导轨的应力、应变和位移以及身管封装部件的应力、应变和位移的变化情况,进而得到离散预紧方式下身管的封装性能如下:
1)由于螺栓的初始预紧作用,身管在未施加电流时有一定的初始预紧作用,导轨及身管部件存在一定的负位移及初始应力、应变,在身管长度上分布较为均匀,没有波动。
2)电流上升阶段,主导轨应力、应变及位移也逐渐增大,且与电流上升速率成正比;不同位置处的位移及应力应变也出现了一定程度的波动,主导轨在螺栓处的位移量小于其他位置,呈现“波浪”状,而应力、应变则没有明显的变化规律。应力、应变变化较大,起伏波动明显,且没有明显的规律。电流维持在峰值后,导轨及身管上同一位置的应力、应变及位移仍不断增大,但增大速率较小。但不同位置处,各参量的变化增大。
3)身管部件最大的应力、应变及位移变化规律与主导轨的变化规律相同,且最大值出现在主导轨附近的绝缘材料上。最大位移量小于主导轨的位移量,表明绝缘材料与主导轨间没有缝隙,保证了身管的封装性能。
计算结果可以看出,兆安级电流激励条件下,采用螺栓连接方式的身管,在螺栓预紧条件下能够满足身管封装要求。
References)
[1]HILMAR P, FRANCIS J,VOLKER W. Technical aspects of railguns[J]. IEEE Transactions on Magnetics, 1995,31 (1): 348-353.
[2]FAIR H D. Electromagnetic launch: a review of the U.S. national program[J]. IEEE Transactions on Magnetics, 1997,33 (1): 11-16.
[3]FAIR H D. Electromagnetic launch science and technology in the United States enters a new era[J]. IEEE Transactions on Magnetics, 2005,41 (1): 158-16.
[4]FAIR H D. Advances in electromagnetic launch science and technology and its applications[J]. IEEE Transactions on Magnetics, 2009,45 (1): 225-230.
[5]DAVID C H ,STEVEN G. U K electric gun national overview[J]. IEEE Transactions on Magnetics, 2003,39 (1): 18-21.
[6]TREVOR E J ,DAVID C J. Contact pressure distribution and transition in solid armatures[J]. IEEE Transactions on Magnetics,2001,37 (1): 81-85.
[7]BARBER J P, BAUER D P, PARKER J V, et al. A survey of armature transition mechanisms[J]. IEEE Transactions on Magnetics,2003,39 (1): 47-51.
[8]MCNAB I R, CRAWFORD M T, SATAPATHY S S, et al. IAT armature development[J]. IEEE Transactions on Plasma Science, 2011,39 (1): 442-451.
[9]GUO Wei,ZHANG Tao,LI Juxiang, et al. Design and testing a novel armature on railgun[J]. IEEE Transactions on Plasma Science, 2015, 43(5): 1119-1124.
[10]GEORGE A,PROULX G A. Railgun with steel barrel sections and thermal management system[J].IEEE Transactions on Plasma Science,2015,43(5):1642- 1646.
[11]STONKUS R,RACKAUSKAS J,SCHNEIDER M,et al. Structural mechanics of railguns with open barrels and elastic supports: the influence of multishot operation[J]. IEEE Transactions on Plasma Science, 2015, 43(5): 1510-1515.
[12]LI Mingtao,YAN Ping,ZHOU Yuan, et al. Simulations on elastoplasticity of the monolithic aluminum armature under the contact force[J]. IEEE Transactions on Plasma Science, 2011,39 (1): 426-430.
[13]STEFANI F,CRAWFORD M,MELTON D,et al. Experiments with armature contact claddings[J]. IEEE Tran-sactions on Magnetics,2007,43 (1): 413-417.
[14]陈庆国,王永红,魏新劳,等. 电容驱动型轨道电磁炮电磁过程的计算机仿真[J]. 电工技术学报,2006,21 (4): 68-71.
CHEN Qingguo, WANG Yonghong, WEI Xinlao, et al. Computer simulation of electromagnetic process in the capacitor drived rail gun[J]. Transactions of China Electrotechnical Society, 2006,21 (4): 68-71.(in Chinese)
[15]巨兰,张碧雄. 电磁轨道炮的炮体结构设计[J]. 舰船科学技术, 2011,33 (7): 94- 98.
JU Lan,ZHANG Bixiong. Barrel structural design and research on electromagnetic railgun[J]. Ship Science and Technology,2011,33 (7): 94- 98.(in Chinese)
[16]吕彦,任泽宁,赵鸿燕,等.电磁轨道炮身管结构的研究概况[J].兵器材料科学与工程,2012,35(1):93- 96.
LYV Yan,REN Zening, ZHAO Hongyan, et al. Research status of electromagnetic rail gun barrel structure[J]. Ordance Material Science and Engineering, 2012,35 (1): 93- 96.(in Chinese)
The Encapsulation Performance Analysis of Series Enhanced Electromagnetic Railgun with Bolt Pre-tightening
SHI Jiangbo,LI Baoming
(National Key Laboratory of Transient Physics,Nanjing University of Science and Technology,Nanjing210094,Jiangsu,China)
For the purpose of studying the encapsulation performance of series enhanced electromagnetic railgun with bolt pre-tightening, calculated was the electromagnetic force of the rails from the perspective of electromagnetic field with the stress, strain and displacement of the gun barrel achieved. Then a three dimensional series enhanced railgun tube model was built, and a ramp current was loaded to calculate the changing law of rail stress, strain and displacement. And these parametrical varying patterns of the barrel units were also obtained. As the calculation results show, under the condition of the blot pre-tightening, the rails and the barrel units are under the impact of certain initial displacement, stress and strain. With the gradual increase of the current and duration, the parameters of rail and barrel units were increased gradually with an obvious fluctuation pattern. The rail displacement in the bolt position shows obvious drop trend. And the displacement of barrel units was smaller than that of the rail, so the rail and the barrel unit can have good contact condition. This phenomenon demonstrates that the use of discrete seal barrel with bolt pre-tightening can control the maximum displacement of the rail to a certain extent, which works well for the barrel encapsulation performance.
series enhanced;electromagnetic railgun;discrete seal;blot pre-tightening;encapsulation performance
2015-05-27
石江波(1987—),男,博士研究生,主要从事电磁发射技术研究。E-mail:shijiangbo2002@163.com
TJ02
A
1673-6524(2016)01-0001-06

