基于OptiStruct的床身结构尺寸优化策略研究
周 浩,丁晓红,张 横
(上海理工大学 机械工程学院,上海 200093)
基于OptiStruct的床身结构尺寸优化策略研究
周浩,丁晓红,张横
(上海理工大学 机械工程学院,上海 200093)
针对传统设计方法设计的床身结构笨重的问题,以某型数控外圆磨床床身为例,在轻量化设计过程中提出一种尺寸优化策略,运用OptiStruct软件对床身结构的垫铁位置进行优化设计,在基于灵敏度分析对床身结构进行尺寸优化设计。优化结果表明,优化后床身的第一阶固有频率提高5.74%,重量减轻7.15%,验证了该尺寸优化策略在床身结构轻量化设计中的可行性及有效性。
机床床身;垫铁位置优化;灵敏度分析;尺寸优化
磨床床身是磨床的重要支撑部件,其起着支撑工作台、砂轮架、头架和尾架等关键部件的作用,其结构特性直接影响机床的加工精度、精度稳定性和生产效率,因此如何控制床身的结构静动态特性是磨床设计的主要问题之一[1-2]。磨床床身结构是典型的支撑箱型结构,床身内部加强筋与外壁厚度参数选取多数采用经验设计,由于追求其高安全系数,设计过于保守,使得磨床床身结构重量大、消耗材料多,无法满足高端机床高精度、高效率和低能耗的设计要求,因此对机床床身进行轻量化设计研究具有重要意义,优良的机床结构设计可使用户获得良好的机械性能和更大的经济优势[3-5]。
传统的床身设计大多数采用静态力学的简化计算和经验设计为基础的常规方法,尽管该设计方法经过实践证明有一定的可靠性,但存在设计周期长、设计过于保守等弊端,随着计算机的发展,有限元法逐渐广泛用于工程领域,实现了计算机和有限元理论的结合,大幅提高了工程领域结构设计的效率和质量。采用有限元软件建立机床结构的静动态模型以及成为机床理论建模的普遍方法[6-7]。目前机床床身结构内部的加强筋多是井字筋,横向与纵向筋板交叉分布,仅通过简单的尺寸优化设计,有时优化迭代过程不收敛,寻求不到尺寸变量的最优解,即使迭代过程收敛,寻求到尺寸变量最优解,床身的静动态特性提升的幅度也较小。目前床身轻量化研究中,主要通过改变床身的结构来大幅度提高床身的静动态性能,已有不少研究成果,另一方面使用新型复合材料代替传统的床身铸铁材料,由于研究技术不够成熟、材料成本昂贵等原因,材料替代技术还没有广泛用于床身的优化设计中。
本文以某型数控外圆磨床床身为研究对象,为实现床身结构的轻量化,提出了一种尺寸优化策略,该策略分为两步:第一步运用OptiStruct软件对床身结构的垫铁位置优化,寻求出垫铁分布的最优位置,该步旨在大幅度提高床身的静动态特性;第二步为基于灵敏度分析,选择出关键性设计变量,再对床身进行尺寸优化,该步旨在降低床身的重量。最后根据有限元方法对优化前后床身结构静动态性能对比分析,验证了该尺寸优化策略在床身结构轻量化设计中的可行性和有效性。
1 床身结构垫铁位置优化设计
结构刚度是评价机床床身结构性能的一个重要指标[8-10],影响床身结构刚度的主要因素有结构形状、支撑位置、材料特性、热处理工艺性等。磨床通过减震垫铁与地面实现弹性联接,以减少振动的相互传递,因此磨床垫铁支撑位置对于床身结构静动态性能有很大影响。对床身支撑位置进行优化设计,寻求垫铁最优支撑位置,可以在不改变机床结构的情况下,仅通过移动磨床床身结构垫铁支撑位置就可以达到提高机床的性能的目的,具有广泛的应用价值。
本文以某型数控外圆磨床床身为例,该型号磨床主要包括的5个部分:磨床床身、头架、尾架、工作台和砂轮架;如图1所示为该型号床身结构,该床身是典型的T型床身结构,分为前床身和后床身两部分,前床身分布两条导轨,分别为V-导轨和平导轨,材料为HT250,结构重量达3 500 kg,床身整体结构偏重。
磨床床身承载的载荷主要为床身上其他机床部件的重量,头尾架、工件等部件通过工作台作用于前床身,砂轮架、砂轮等通过砂轮架垫板作用于后床身。由于工作台在前床身运动,前床身受到移动载荷的作用,为充分考虑磨床床身所受载荷的情况,对前床身3个特殊位置分别加载,对3个位置按3个工况来处理,如图2所示为床身左极限工况,此时工作台位于前床身导轨的左极限处,同理,中间位置工况时工作台位于前床身导轨的正中间处;右极限工况时工作台位于前床身导轨的右极限处,3种工况下砂轮架垫板位置均保持位置不变。

图1 床身结构示意图

图2 床身左极限工况
该磨床由10块垫铁作为支撑,其垫铁位置如图3所示,在底面8个角部均有一块垫铁,在前床身平导轨下方分布两块垫铁。该垫铁位置分布的优点是易于安装与拆卸,但这种经验安装方式并不能保证机床在该支撑方式下机械性能达到最优,通过优化方法确定垫铁最优位置可以在不改变机床结构的情况下有效提高机床的机械性能。
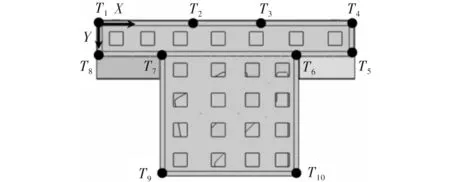
图3 优化前垫铁位置示意图

图4 优化后垫铁位置示意图
床身性能的主要评价指标是静刚度和动刚度,在静刚度的设计上,考虑到床身V-轨X方向的变形对加工精度影响最大,为避免导轨变形波动大,故选用导轨变形方差来控制导轨变形的幅值,使导轨的变形趋于一条直线;在动刚度设计上,则通过第一阶固有频率来保证。故垫铁位置优化设计中,以导轨变形方差最小与一阶固有频率最大作为设计目标,以床身垫铁位置为设计变量,对垫铁位置进行多目标优化设计,数学模型如式(1)所示
(1)

选取床身左上角顶点为原点如图3所示,其他垫铁位置坐标以此为参考,优化后垫铁位置如图4所示,其中垫铁T6、T7相对移动的距离;垫铁T4位置没有发生变化,其余垫铁均有向床身内侧移动。优化前后垫铁具体位置对比如表1所示。

表1 优化前后垫铁位置对比
尺寸优化策略的第一步,主要是通过垫铁的位置优化来大幅度提高床身的静动态性能,如表2所示,垫铁优化前后床身第一阶固有频率与V-轨变形方差对比。

表2 垫铁优化前后参数对比
2 床身结构尺寸优化设计
本文结构尺寸优化[11-12]是在上一步垫铁位置优化设计的基础上进行的,对其内部的横、纵筋板及外壁等7个厚度参数进行的尺寸优化,以寻求性能最佳、重量最轻的床身结构。
设计变量的优劣对优化结果有较大的影响,有时会造成优化迭代过程不收敛,寻求不到最优值[13]。因此,尺寸优化前先通过灵敏度分析来筛选设计变量,不仅可选择出关键性的设计变量,而且设计变量个数的减少能提高尺寸优化的效率。床身结构的质量和柔度随筋板和外壁的厚度改变而变化,灵敏度分析就是选取对床身质量和柔度影响关键的参数作为优化设计变量,然后通过尺寸优化实现轻量化设计。采用试验设计(Design of Experiment, DOE)方法来构建近似模型,在近似模型中对各个变量进行灵敏度分析。
根据床身的结构特点,选出7个变量如图5所示,本设计采用 Optimal Latin Hypercube方法对床身结构的7个变量进行DOE分析,DOE分析过程包括以下两个步骤。
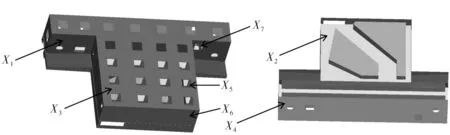
图5 尺寸变量示意图

图6 尺寸变量对质量和柔度响应的变化率
从图6(a)可以看出,7个尺寸变量对底座的总质量成正比关系,尺寸变量X5、X6对底座质量影响最大,因为其直线斜率最大,其余尺寸变量对其影响相对较小;图6 (b)中X6对柔度的影响最大;从图6(a)和图6(b)对比可得出,X1与X4两变量对质量和柔度影响上,斜率均很相近,也说明两者对两目标响应作用效果近似相同,故将两变量合为一个变量Xh;X2与X3由于随之尺寸的变化两者变化率均很小,故不作设计变量;X7对质量的影响较大而对柔度的影响较小,故选作设计变量。由以上分析,选择Xh、X4、X6、X7共4个尺寸变量作为优化设计的变量。
优化过程中数学模型的选取是一个难点,由于是进行床身轻量化设计,因此把床身质量最小作为设计目标。磨床床身中V-轨水平方向的变形对加工的精度影响最大,故通过约束V-轨水平方向的平均变形来保证结构静刚度;通过约束第一阶固有频率来保证优化后结构的动刚度。设计变量为上步运用灵敏度分析技术筛选出的4个设计部分的厚度。如式(2)为尺寸优化数学模型
(2)

如图7所示尺寸优化的迭代历程图,当迭代次数为17次时,达到收敛条件迭代终止。表3所示为各设计变量初始值和优化后的结果。

图7 迭代历程图

设计变量初始值/mm下限/mm上限/mm优化值/mm说明Xh30153522两导轨长度方向支撑面X525153020后床身筋板X625153025床身外壁X725153020前床身筋板
3 优化前后结果对比
采用有限元分析方法,建立优化后床身有限元模型,施加载荷边界条件,对优化后床身模型进行力学性能分析,并与优化前床身结构的力学性能相对比,得出如表4所示的优化前后床身V-导轨变形量对比。

表4 优化前后床身V-轨变形量对比
从表4可得出,优化后床身结构各工况下V-轨的合位移、水平方向变形量均降低,说明床身结构的静刚度有所提高。如图8为优化前后V-轨在中间位置工况下水平方向变形曲线,如图9为优化前后V-轨在中间位置工况下水平方向变形云图。

图8 优化前后V-轨在中间位置工况下水平方向变形曲线

图9 优化前后V-轨在中间位置工况下水平方向变形云图

性能对比优化前优化后变化率质量/kg35373284-7.15%第一阶固有频率/Hz223.0235.8+5.74%
优化前后床身重量与第一阶固有频率变化如表5所示,优化后磨床床身的第一阶固有频率提高5.74%,重量减轻7.15%。综上所述,床身的动静态性能均得到提高,且床身重量降低,达到了优化设计的预期目的。
4 结束语
本文以某型数控外圆磨床床身为例,针对磨床床身轻量化设计,提出了一种尺寸优化策略,首先对垫铁位置进行优化设计,然后在此基础上基于灵敏度分析进行尺寸优化。通过优化前后床身结构性能对比,优化后床身静动态性能均得到提高且重量降低,验证了该尺寸优化策略方法的可行性、有效性,该方法为改进床身结构和改善整机工作性能提供了一定的理论依据,并可推广到其他机床床身结构优化设计中。
[1]C.Brecher,P.Utsch,R.Klar,C.Wenzel.Compact design for high precision machine tools[J].International Journal of Machine Tools Manuf,2010,50(4):328-334.
[2]杨勇,张为民,李鹏忠.基于动态灵敏度分析的数控机床床身结构优化设计[J].机械科学与技术,2012,28(9):49-52.
[3]邢晓辉,王洪川,王贵飞,等.基于灵敏度分析的数控机床床身尺寸优化设计[J].组合机床与自动化加工技术,2013(11):5-8.
[4]孙晓辉,丁晓红,王师镭,等.高刚度轻质量的机床床身优化设计方法研究[J].机械科学与技术,2013,32(10):1461-1465.
[5]任帅,宋冬冬.基于ICM拓扑优化的加工中心床身轻量化设计[J].机床与液压,2014(13):130-134.
[6]王钰栋,金磊,洪清泉,等.HyperMesh&HyperView 应用技巧与高级实例[M].北京:机械工业出版社,2012.
[7]洪清泉,赵康,张攀,等.Optistruct&Hyperstudy 理论基础与工程应用[M].北京:机械工业出版社,2010.
[8]范文杰,范子杰,苏瑞意.汽车车架结构多目标拓扑优化方法研究[J].中国机械工程,2008(12):1505-1508.
[9]罗辉,陈蔚芳,叶文华.机床立柱灵敏度分析及多目标优化设计[J].机械科学与技术,2009,28(4):487-491.
[10] 陈叶林,丁晓红,郭春星,等.机床床身结构优化设计方法[J].机械科学与技术,2010,27(8):65-68.
[11] Kroll L,Blau P,Wabner M,et al.Lightweight components for energy-efficient machine tools,CIRPJ[J].Manufacture Science Technolcgy,2011,4(2):148-160.
[12] 王赢利.新能源汽车白车身结构拓扑及尺寸优化设计[D].大连:大连理工大学,2012.
[13] 杨玉萍,张森,季彬彬,等.龙门加工中心横梁关键尺寸灵敏度分析与优化[J].制造业自动化,2013(16):110-112.
Sizing Optimization Strategy for Machine Tool Bed Structure Based on OptiStruct
ZHOU Hao, DING Xiaohong, ZHANG Heng
(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)
A typical bed structure of a cylindrical grinding machine is studied as an example in lightweight design, and a strategy divided into layers of sizing optimization is put forward. The pad iron layout is optimized as the first layer with OptiStruct with the second layer based on sensitivity analysis to optimize the size of bed structure. The optimized results show that the first natural frequency increases by 5.74% and the weight decreases by 7.15%, indicating that the strategy of sizing optimization is feasible and effective.
machine tool bed structure; pad iron layout optimization; sensitivity analysis; sizing optimization
10.16180/j.cnki.issn1007-7820.2016.08.028
2015-11-25
上海市教委科研创新重点基金资助项目(13ZZ114)
周浩(1990-),男,硕士研究生。研究方向:结构分析与优化设计。丁晓红(1965-),女,博士,教授,博士生导师。研究方向:机械系统和结构现代设计理论。
TP202+.7
A
1007-7820(2016)08-096-05

