塔式起重机起重臂接触应力计算分析

闫　萌，黄　鑫，郑倩倩，赵　香

（长安大学道路施工技术与装备教育部重点实验室，陕西西安710064）

塔式起重机起重臂接触应力计算分析

闫萌，黄鑫，郑倩倩，赵香

（长安大学道路施工技术与装备教育部重点实验室，陕西西安710064）

以塔式起重机的起重臂为研究对象，运用Hertz接触理论，在最大起重载荷工况下分析变幅机构与起重臂接触过程中的局部接触应力。利用ANSYS软件对Hertz接触理论计算结果进行应力校核。根据Hertz理论计算结果与ANSYS有限元分析结果对实际工况下的起重臂与变幅机构进行分析，得出塔式起重机起重臂在最大起重载荷工况下满足设计要求。

起重臂；赫兹理论；接触应力；ANSYS

随着高层、板式建筑结构的增多，塔式起重机的满载率加大，工作繁忙程度加重，有些塔式起重机大部份工作时间在高应力水平下运行，以前的设计手段已经不能满足现代塔式起重机的发展了［1］。本文以一种Qtk16快架塔机为研究对象，计算分析该快架塔机的起重臂与变幅小车的接触应力。在工作环境下，起重臂承受变幅小车轮和吊臂对下弦杆轨道的交变载荷［2］，从而产生局部应力集中，造成局部失稳，但在运用截面法进行设计时强度又满足要求。在实际的工作过程中属于高应力状态，因此，有必要在最大起重载荷工况下对起重臂进行局部稳定性分析。快架塔机Qtk16的起重臂由6.3#角钢焊接而成，小车在工作过程中紧靠四个小车轮承重，接触为面面接触，将产生较大的接触应力，属于接触力学的范畴。起重臂与变幅小车模型如图1所示。

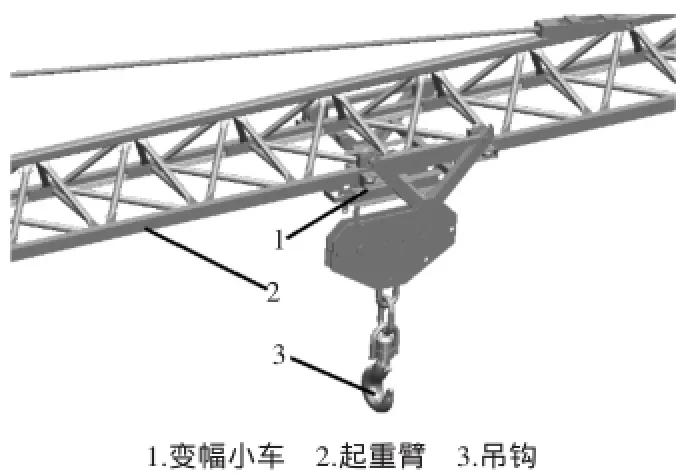
图1　快架塔起重臂与变幅小车

在实际的工况过程中，快架塔在大部分的工况过程是小车和吊钩吊着起重物在起重臂架上运动。由于小车在起重臂上的位置不同，快架塔的起重质量不同。根据快架塔作业幅度与起重量关系，本文选取最危险工况，起重质量为1 500 kg的工况进行分析，运用Hertz（赫兹）理论的理论基础对起重臂在该工况下的变幅小车对起重臂的接触应力进行分析。

1　接触应力分析基本理论

根据赫兹理论和弹性力学中的相关知识，当接触物体本身的尺寸与接触尺寸相比很大，则在此区域中的应力就不依赖于物体原理接触区的形状，也不依赖于支撑物体的确切方式，这样可将每一物体看作是以平表面为界的半无限弹性固体即弹性半空间［3］。图2为起重臂与小车轮之间的工作时的接触简图。其中R为小车轮的轮半径，G为小车轮的承重，L为小车轮的宽度。小车轮的滚动圆与起重臂下弦杆的中心线（在以下计算过程中将此中心线称为Z轴）相接触的情况。变幅小车与起重臂的断面形状尺寸比小车轮与起重臂的接触处尺寸大得多，故按两个弹性半空间无限体接触处理，其接触应力的分布p为椭圆形分布，赫兹接触应力公式：

式中：x为接触点到滚轮中心线Z轴的距离；p0为最大接触应力；a为接触边缘处在Z轴的投影距离。

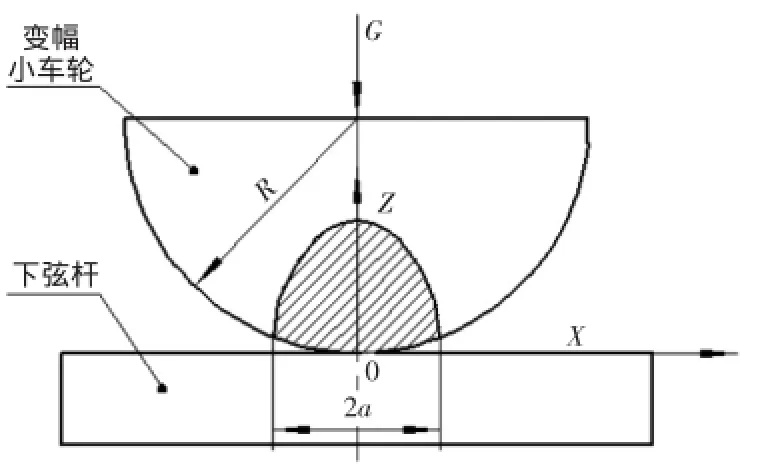
图2　小车轮与起重臂接触简图

根据Hertz理论最大接触应力p0为：

式中：G为小车轮的承重；L为小车轮的宽度。

将式（2）代入式（1）中有：

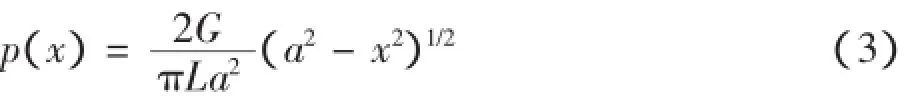
由式（3）知接触压力在接触处边缘降为零。

由于接触宽度远远小于小车轮的轮半径，根据半无限半空间平面进行分析可得出接触区域半宽公式式（4），最大接触应力为公式（5）。

式中：R为小车轮的轮半径。

从上两式中可以看出，小车轮与起重臂接触面积大小和接触应力都与外载荷、小车轮半径R、小车轮宽度L有关。故在设计过程中可以各参数控制来减小接触应力。通过应力分布式，可以求出两物体的内部应力。根据材料力学强度理论对其进行校核，可得Z方向上的最大等效应力为：

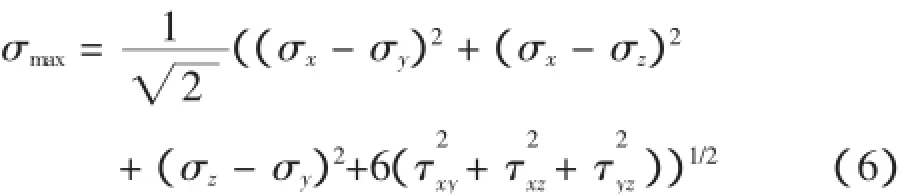
2　起重臂与小车接触应力计算

本文以Qtk16型快架塔机为研究对象，分析快架塔机起重臂与变幅小车接触部位应力情况。根据快架塔机各参数为：吊钩G1=57 kg，变幅小车G2=48 kg，最大工况下载荷G3=1 500 kg，小车轮半径R=45 mm，小车轮宽度L=30 mm，其中小车轮的材料为45#钢，下弦杆的材料为Q235B，其中45#钢的屈服极限为300 MPa，强度极限为455 MPa.Q235B的屈服极限为235 MPa，强度极限为375MPa.取两种材料的弹性模量E1＝E2=210 GPa，泊松比v1＝v2=0.3.将快架塔机的各参数代入式（4）和（5）有：

a=0.510 mm，p0=654MPa

起重臂与变幅小车在接触部位的的Z轴上点的等效应力为：

利用MATLAB对（7）式求解最大值。求解得当Z=1.38 mm时，小车轮所受的最大等效应力为σmax=364.62MPa.小车轮材料为45#钢，其强度极限为455 MPa.下弦杆的材料为Q235B，强度极限为375 MPa，不小于最大等效应力365MPa，故设计满足要求。

3　起重臂与小车的ANSYS接触分析

3.1接触分析

ANSYS可以将接触分析类型细分为三种类型，分别为点－点接触、点－面接触和面－面接触，不同的接触类型适应于不同的分析模型。在此例中的小车轮与下弦杆的接触属于面面接触。

为了验证理论计算得正确性，利用ANSYS软件对Qtk16型快架塔机的起重臂与变幅小车进行接触应力的分析。此例中小车轮与起重臂的接触属于面面接触，故对该模型可简化成二维平面问题。经收敛性试算，选择单元类型Plane42号单元的二维平面来模拟滚轮和起重臂的下弦杆接触问题。接触算法采用Lagrange&Penalty，接触区域的网格大小应小于半宽大小，采用mapped的映射网格划分，位移边界条件为下弦杆底边的全约束。分析变幅小车的受力情况，故在小车轮的中心处加载，G=（G1+G2+G3）/4=401.25 kg.

3.2结果分析

根据Mises屈服准则，在接触过程中的小车轮等效应力最大为305.033 MPa，起重臂的最大等效应力为343.162MPa.在ANSYS后处理中选取小车轮与起重臂的接触应力进行分析，可以看出接触应力最大为p0=412.89MPa.

分析其结果有：由图3可知，在Mises屈服准则下，最大等效应力发生在小车轮与下弦杆接触的位置，小车轮最大的等效应力为305.033MPa，但小车轮的强度极限为455 MPa，起重臂的接触应力为343.162 MPa，起重臂的强度极限为375 MPa，故而这是满足强度要求，与理论计算相符。分析图3中的应力分布情况，由于载荷的施加位置在小车轮的中心节点处，故在该节点附近会产生应力集中现象，在Z方向上会有应力的产生。从图3可以看出接触区域为椭圆形，与Hertz理论下的接触区域形状相符，基本满足理论的分析结果；在ANSYS的后处理中接触应力p0=412.89 MPa，因为接触区域网格划分的原因，使得用接触应力评判接触区域时的接触形状与理论计算时的有一定的偏差，最大接触应力位置为Z轴方向。

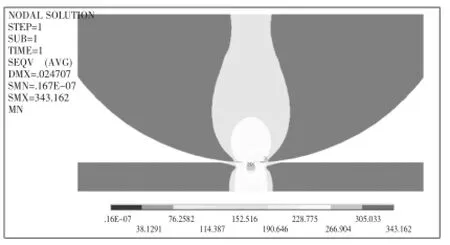
图3　 Mises接触区域图

分析其存在偏差的影响因素，可归纳为如下三点：1）实际工况下的接触过程更加复杂，赫兹理论的理论计算是在考虑物体小变形前提下得到的。而ANSYS的仿真考虑了材料在受力情况下的塑性变形，接触面积的增大而导致接触应力的减小；2）采用二维平面应力分析中网格划分过疏或者过密都会对结果产生影响，在接触面的网格划分时应使单元长度小于接触区域最小半宽；3）有限元数值接触算法是以迭代为基础的，所以在迭代计算中会产生累积误差。

4　结束语

本文通过赫兹理论对快速架设塔式起重机的起重臂局部稳定性进行研究，并用ANSYS软件进行理论校核。在理论校核中仿真的是快架塔Qtk16在最大起重载荷工况下的接触应力，起重臂在最大起重载荷工况下满足强度要求，故起重臂的设计强度要求满足。另外，起重臂和变幅小车的往复运动可能会造成下弦杆材料的屈曲失效，本文的小车轮与起重臂间的接触应力分析为以后的起重臂的屈曲分析提供了依据。

［1］王进.基于有限元法的塔式起重机钢结构疲劳寿命研究［D］.重庆：重庆大学，2005.

［2］肖冬桂.塔机疲劳剩余寿命预测系统研究［D］.长沙：中南大学，2013.

［3］卢哲安.混凝土桥光纤光栅监测与复合铺装结构研究［D］.武汉：武汉理工大学，2013.

The Contact Stress Calculation and Analysis of Tower Crane Boom

YAN Meng，HUANG Xin，ZHENG Qian-qian，ZHAO Xiang
（Key Laboratory for Highway Construction Technology and Equipment ofMinistry of Education Chang’an University，Xi’an Shaanxi 710064，China）

Take the tower crane boom as research object，analysing the local contact stress of the contact process of luffing mechanism and boom in the maximum lifting load condition by using Hertz contact theory.Checking the calculation of Hertz contact theory by using the ANSYSSoftware.According to the calculation of Hertz theory and the analytic result of the ANSYS Software to analyse the boom and luffing mechanism in the actual working conditions，inferring that the tower crane boom atmaximum lifting load conditions canmeet the design requirements.

boom；Hertz theory；contact stress；ANSYS

TH212

A

1672-545X（2016）06-0044-03

2016-03-20

闫萌（1990-），男，河南漯河人，在读硕士研究生，研究方向为机械设计。