车车事故再现方法研究

张芳，周华，唐灿，刘娜（西华大学汽车与交通学院，四川 成都 610039）



车车事故再现方法研究

张芳，周华*，唐灿，刘娜
（西华大学汽车与交通学院，四川 成都 610039）

为研究车车碰撞过程中，事故各参数对再现车速的影响，根据国家车辆事故深度调查体系（NAIS）中的一个真实案例，利用基于能量模型的定值分析法及不确定度分析法进行数据计算分析，在此基础上利用 Pc-Crash仿真软件进行事故再现。以车辆实际损坏信息、最终相对位置等信息为评价标准，比较定值分析法及不确定度分析法，并分析事故参数不确定因子对车速影响。

车车碰撞；事故再现；不确定度分析

10.16638/j.cnki.1671-7988.2016.08.090

CLC NO.: U467Document Code: AArticle ID: 1671-7988(2016)08-261-04

引言

我国车车道路交通事故形态一般包括：正面碰撞、侧面碰撞、追尾碰撞、同向刮擦、对向刮擦、其他角度碰撞、碰撞静止车辆、其它等8种。据道路交通事故2013年度统计年报显示，我国年度车车道路交通事故总数为127345起，其中车辆正面相撞占总数的10.4%，涉及伤亡人数3.3万余人，人员财产损伤严重，因此车车碰撞事故的分析与再现是事故鉴定中的重点研究问题。文献[1]中采用能量模型对碰撞车速进行不确定理论分析，其中事故车辆碰撞前制动距离及碰撞后滑行距离为定值；文献[2]中分析了车辆与二轮自行车碰撞事故中车速多值计算问题，建议采用不同方法进行多级综合评定。

近年来，车辆保有量的不断增加，且行车安全意识不足，导致车车事故的比重也不断增大，但随着社会发展及法规完善，人们对车速评估及责任认定的关注和要求也不断提升。因此，本文将根据车车正碰的国家车辆事故深度调查案例，通过不确定度分析法深入分析各不确定因子对车速的影响，并通过Pc-Crash仿真来检验数据分析结果，旨在为事故认定和事故善后处理提供参考依据。

1、深度调查事故案例

该事故数据来源于国家车辆事故深度调查体系，主要用于验证这些模型的可行性及求解结果分析。

某一车车正面碰撞事故：甲车沿老成彭路由成都往新繁方向行驶，乙车沿老成彭路由新繁往成都方向行驶。由于甲车驾驶员操作判断失误，逾越至乙车所在车道，造成逆向行驶，导致两车正面全宽区域发生正面碰撞。碰撞后，两车各滑行一段距离，并最终停止在行驶车道内。事故导致两车前部明显损坏，两车正面安全气囊均正常点爆，驾驶员无伤亡。事故现场图如图1所示。

根据事故现场图、事故现场照片及车检细节信息可以获得相关参数的对应取值，具体取值情况如表1所示。

表1　事故车辆相关参数

2、车速分析

2.1能量法车速计算模型

车车碰撞过程一般可分为碰撞前、碰撞及碰撞后三个阶段，故车辆本身具有能量的损耗也分别存在于这三个阶段。通常在进行车车碰撞分析时，考虑到由于正面碰撞的两车之间相对速度较大，车辆变形多数为塑性变形，而弹性变形较小，可忽略不计，故简化为在该正面碰撞过程中没有弹性恢复阶段，车辆产生的变形全部为塑性变形。

车辆碰撞前为事故车辆驾驶员发现危险到事故发生时的过程，该阶段的车辆行驶状态主要取决于驾驶员的措施。驾驶员进行紧急制动时，事故现场会留下制动拖印。根据牛顿第二定律及能量守恒定律，可据此制动拖印获得相对应的等效速度，有

其中：t为制动器反应协调时间s，取0.2s；μ为车辆滑移时的附着系数；L1为车辆碰撞前的制动印迹m

正面碰撞时，车辆前部溃缩变形，根据轿车的正面碰撞实验，车体塑性变形量x与有效碰撞速度的关系由方程表示为：

其中：φ为等效车速与车辆塑形变形间的比例常数，一般由经验公式得出。

两车正面碰撞时，塑性变形量与有效碰撞速度之间存在线性关系，即：

碰撞结束后，车辆仍具有部分剩余能量，会继续做相应运动，一般为滑行运动，则该阶段能量损耗所对应的等效速度[3]。

其中，L2为车辆碰撞后的滑移距离m

则事故发生前，车辆的行驶速度为：

2.2车辆估算车速的不确定度分析

早在1927年，德国物理学家海森堡就最先提出“不确定度”概念[4]。具体来说，不确定度是定量地表示了随机误差和未定系统误差的综合分布范围，它可以近似地理解为一定置信概率下的误差限值。

在实际的交通事故中，事故现场勘测数据及车损信息总是包含很多不确定性因素，合理分析这些不确定性因素对交通事故的再现结果有重要的现实意义。不确定度评定的一般流程如图2所示[5]。

文献[1]中，针对一起小客车追尾大货车事故以能量算法模型为基础进行了不确定度分析。该事故中，碰撞前小客车的制动距离以及碰撞后两车滑行距离为准确定值，而实际生活中，由于现场情况及人为客观原因等，车辆的制动距离都为一估计值。一方面，本文引入制动距离不确定因子，进行不确定度分析；另一方面，针对速度分量、碰撞车速均进行不确定度分析。

1）碰撞前：将事故车辆制动距离、地面附着系数设为不确定因子。

2）碰撞时：将事故车辆前部塑性变形尺寸设为不确定因子。

3）碰撞后：将事故车辆滑移距离、地面附着系数设为不确定因子。

2.2.1制动距离、滑行距离为定值

两车的制动距离、滑行距离分别取值为：甲车，L1=7.3、L2=0.14；乙车，L1=5.9、L2=0.42。不确定度分析结果如表2所示。

表2　不确定度分析结果

（*为比较不同取值的计算结果，甲车相关距离取最大值，乙车相关距离取最小值）

碰撞前车速分别为：

我们可以看到译文2将译文1中表达事物过程的功能成分隐喻为由该动词派生而来的形容词，这是韩礼德十三种概念隐喻类型的第五种。具体的过程被隐喻化为性质，从而使内在的逻辑关系体现得更为明确、表达更加严谨。同时，与译文2对比，译文1对于专业名词的处理也不是特别正确，因此，在平时的学习中专业学习者一定要积累相关的英文表达，查询专业的词典，切忌胡乱翻译。

2.2.2制动距离、滑行距离为不确定因子

制动距离、滑行距离均作为不确定因子，不确定度分析结果如表3所示。

表3　不确定度分析结果

碰撞前车速分别为：

2.3事故再现——PC-Crash仿真分析法

20世纪以来，计算机仿真技术快速发展，同时由于真实试验的高成本、不可重复性等客观原因，其普及性和可行性不高，因此计算机仿真软件被大量的用于交通事故通还原。目前常用的碰撞类研究软件主要有MADYMO、LS-DYNA、Pc-Crash以及前处理网格划分软件HYPERMESH等，其中Pc-Crash软件是一款典型的进行交通事故模拟及还原交通事故的仿真系统软件[6]，其界面如图2-14所示。Pc-Crash主要通过反推法进行碰撞模拟，主要依据为事故现场所采集的相关数据信息，如车辆初始位置信息、车辆最终停止位置信息、车辆痕迹信息等，并对其进行分析还原。目前Pc-Crash在奥地利、德国、日本、新加坡等国家已成为事故再现方面较重要的分析软件，也是以上各国交通部门进行交通事故分析时必备的软件之一[7]。

基于PC-Crash软件建立事故碰撞模型，分别设置车轮与地面的摩擦因数为0.75、0.85。在事故再现模拟之前，对碰撞车速进行科学预估、碰撞位置进行合理分析，可以提高事故仿真效率和精度。通过上述数据分析，可以得出车辆碰撞速度，预估：V甲车≈47.48～52.45km/h、V乙车≈44.49～50.59km/h，通过调整相关因子得出：

当μ=0.75、V甲车=48.3km/h、V乙车=46km/h；

当μ=0.85、V甲车=51km/h、V乙车=48.5km/h；

上述情况下车辆最终相对位置、车辆损坏情况与现场数据基本吻合。

3、分析结果比较分析

分别通过定制分析法、不确定度分析法、PC-Crash仿真分析法对上述深度案例进行数据分析及仿真再现分析，各车速计算及取值区间结果如表4、表5所示。

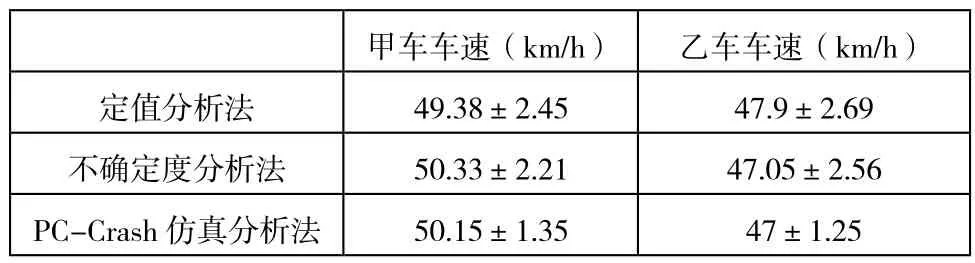
表4　车速计算结果

表5　车速区间优化比较

通过上述分析：

1、由表2、表3显示：当制动距离取定值即采用定值分析法时，碰撞过程第一阶段所占比重变大，大约为不确定度分析法的4倍；第三阶段相反，所占比重变小，约为不确定度分析法的 1/3；相对于不确定度分析法，展伸不确定度也有所增大。分析认为，由于制动距离取定值，导致变化半径变大即标准不确定度变大，在不确定传播系数基本不变的情况下，标准不确定度分量变大，最终使展伸不确定度分量也变大

2、整个碰撞过程中，碰撞第二阶段对车速基准量、展伸不确定度的影响最大；第二、第三阶段产生的影响较小。与实际过程中，两车在碰撞接触过程中能量损耗最大一致，且由于碰撞前制动时间短、碰撞后汽车滑行距离短而消耗的能量小一致。

3、上述三种方法都可以得到车辆事故车速的合理取值范围，当制动距离取定值时，其展伸不确定度偏大，以定值分析法为比较基准，运用不确定度分析法，甲乙两车取值范围分别缩小9.8%、4.8%，运用PC-Crash仿真分析法，甲乙两车取值范围分别缩小45.9%、53.5%。其中当制动距离取值最小（或偏向最小值时），运用定值分析法获得的取值区间的最大值更接近于PC-Crash仿真分析法的优化值（如甲车），其中当制动距离取值最大（或偏向最大值时），运用定值分析法获得的值区间的最小值更接近于PC-Crash仿真分析法的优化值（如乙车）。

4、结论

（1）论文中用三种车速再现方法对一起深度调查案例进行事故再现。这三种方法都可以估算出合理的车速范围，对车车事故的事故重建是可行的，针对事故分析的不同诉求选择快速有效的分析方法。

（2）通过定值分析法和不确定度分析法的比较，针对不同的事故过程应有效的选择数据分析方法，以免使得事故分析结果偏差过大。

（3）Pc-Crash仿真再现需要输入大量的仿真参数，事故建模和计算耗费的时间长，但是仿真精度高，能较好地还原事故过程。通过不确定分析法分析过程可以更好的了解碰撞三个阶段的能量消耗，有助于事故再现的参数调整和理解，快速取得合理的仿真结果。

（4）本文只针对一起车车正面碰撞事故进行了分析，其他类型碰撞事故未考虑，需后续深入研究，验证是否也具有上述影响规律。

[1]袁泉，李一兵.车辆交通事故再现能量方法的不确定评定[J].中国公路学报，2002，23:230—232.

[2]许洪国，高蔚，苏键，等.汽车交通事故碰撞速度多值问题的研究[J].中国公路学报，1996，9(1)；87—93.

[3]刘智敏.不确定度及其实践[M].北京：中国标准出版社，2000.

[4]国家质量技术监督局计量司.测量不确定度评定与表示指南[M].北京：中国计量出版社，2000.

[5]Kiefer,Aaron.A Comparison Study Between Pc-Crash Simulation and Instrumented Handling Maneuvers[J].SAE Paper.2011：2-3.

[6]Hourdos J,Garq V.Accident Prevention Based on Automatic Detection of Accident Prone Traffic Conditions[J].SAE Paper.2009：1-6.

[7]邹铁方，刘雨，刘平凡，等.汽车—摩托车碰撞事故车速及碰撞位置预估方法[J]。中国安全科学学报，2015,25（1）:105-110.

Car accident reappearance method research

Zhang Fang,Zhou Hua*,Tang Can,Liu Na
(Cars and traffic institute of xihua university,Sichuan Chengdu 610039)

For the study of car collision process,the influence of parameter to represent the speed of accident,according to a real traffic accident case in the national vehicle accident in-depth survey system (NAIS),to make data analysis based on the energy model of fixed value analysis and uncertainty analysis,then to make the accident reconstruction using the simulation software PC-Crash.In actual damage information of the vehicle and finally the relative position as evaluation standard,to compare fixed value analysis with uncertainty analysis,and to analyze the uncertain parameter factors influence on the speed of the car in accident.

car-to-car accident; reconstruction of accident; uncertainty analysis

U467

A

1671-7988（2016）08-261-04

张芳（1988—），女，硕士研究生，就读于西华大学，研究方向为汽车安全工程及道路交通事故分析。

简介：周华（1968—），男，副研究员，就职于西华大学，研究方向为道路交通事故机动车技术鉴定和代用燃料汽车技术。

西华大学研究生创新基金（ycjj2015152）资助。