预应力混凝土箱梁剪力滞效应影响因素分析

黄文雄　郑传奇　王　鹏　叶　铮　刘　凯（长江大学城市建设学院）

预应力混凝土箱梁剪力滞效应影响因素分析

黄文雄郑传奇王鹏叶铮刘凯
（长江大学城市建设学院）

为研究预应力混凝土箱梁的剪力滞效应变化规律，选定典型结构的预应力混凝土简支箱形梁，以Ansys有限元分析软件为工具，采用分离式模型，建立了预应力混凝土箱梁有限元模型，重点分析了预应力大小、宽跨比、跨高比、集中荷载大小及内承托长度变化等结构参数对箱梁剪力滞效应的影响。分析结果表明：集中荷载与均布荷载作用下箱梁剪力滞效应分布趋势基本相近，但集中荷载作用下剪力滞效应更加显著；宽跨比对箱梁顶板的剪力滞效应影响最大；随着跨高比的增大，顶板剪力滞系数减小，底板剪力滞系数缓慢增大；预应力在一定程度上可以减小顶板剪力滞效应，加大底板剪力滞效应；而集中荷载大小与箱梁空腔内承托长度的改变对箱梁剪力滞效应的影响不大，可以忽略不计。

桥梁工程；剪力滞效应；有限元分析；预应力混凝土箱梁；影响因素；结构参数

“剪力滞效应”是指翼缘较宽的箱型梁由于翼板中的剪切变形导致纵向正应力沿翼板宽度呈不均匀分布，其间存在传力的滞后现象。“剪力滞效应”的存在将会使混凝土箱梁局部位置产生应力集中，甚至开裂；若忽略剪力滞的影响，就会低估箱梁结构实际产生的应力，从而造成结构的不安全［1-3］。

本文结合前人的研究成果，运用ANSYS有限元软件对预应力混凝土箱梁剪力滞效应及其影响因素进行了详细分析，得出一些有意义的结论［4-6］。

1　箱梁有限元分析模型的建立与结果分析

1.1箱梁有限元分析模型的建立

基于实际工程中箱型梁桥典型结构与尺寸的分析，箱梁采用预应力混凝土简支梁，计算跨径为30m，外荷载采用集中荷载，施加于箱梁腹板顶面。

基于ANSYS有限元分析软件，采用精细化建模技术与参数化建模方法进行建模［7～9］。模型采用分离式模型，采用切分法准确确定预应力筋的具体位置，预应力采用降温法施加［10～12］。钢筋混凝土采用SOLID65单元来模拟，预应力钢筋采用LINK8单元来模拟。箱梁基本尺寸与所建有限元模型如图1所示。

对所建立的有限元模型施加集中荷载（P=40kN）并求解，得到箱梁跨中截面顶板及底板的剪力滞系数，如图2所示。

由图2可知：在集中荷载作用下，顶板的剪力滞效应系数在腹板与顶板的交界处有最大值1.432，边缘处的值最小为0.719，中点处的值为0.921；底板的剪力滞效应系数在腹板与底板的交界处的值最大为1.099，中点处有最小值为0.906。箱梁截面剪力滞效应明显，且顶板的剪力滞效应较底板更加显著。

2　影响剪力滞效应的结构参数分析

影响剪力滞效应的因素较多，本文主要分析的结构参数为：预应力大小、宽跨比、跨高比、集中荷载大小及内承托长度等结构参数对箱梁剪力滞效应的影响。

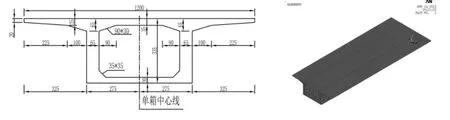
图1　箱梁基本尺寸与有限元模型分析示意图（单位：cm）

图2　箱梁跨中截面顶板、底板剪力滞系数分布图

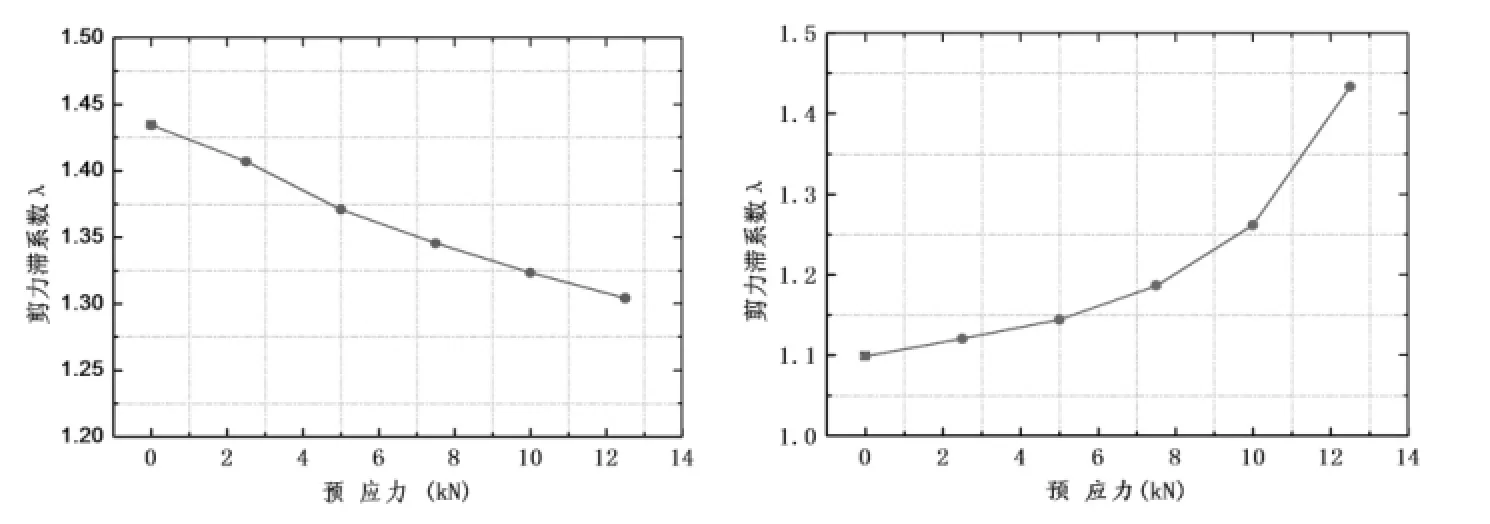
图3　不同预应力作用下箱梁跨中截面顶板、底板最大剪力滞系数变化趋势

2.1预应力大小对剪力滞系数的影响

分别设置预应力大小为：0kN、2.5kN、5kN、7.5kN、12.5kN，保持其他结构参数不变，研究跨中截面最大剪力滞系数。

由图3可知：当预应力为0时，顶板剪力滞系数最大为1.434，底板剪力滞系数最小为1.099；随着预应力的增大，顶板的剪力滞系数大致呈线性减少，底板剪力滞系数越来越大，且其增大的速率越来越快。当预应力增大到12.5kN时，顶板剪力滞系数减小了约9.1%，底板剪力滞系数增大了约30.5%。故而，预应力在一定程度上可以减小顶板剪力滞效应，加大底板剪力滞效应；且对底板的剪力滞效应影响要比顶板更明显。

2.2宽跨比对剪力滞系数的影响

箱梁的计算跨径为30m，考虑宽跨比（B/L）分别为0.2，0.3，0.4，0.5，0.6，0.7，0.8，研究简支箱梁在竖向集中荷载作用下的跨中截面最大剪力滞系数。

1.2 跑步分享：跑者身份的展演 客我身份认同不仅需要个体具有清晰的自我感，同时还需要获得他者明确的信赖感。当通过跑步运动消费形塑了阳光健康的身体形象和坚定勇敢的内在品质而获得一种自我感之后，跑步运动分享又为这种“跑者”的身份和形象提供了一个展演的平台，通过自媒体平台传播自我个性化图景和感悟的“印象管理”方式，收获他者的关注和肯定，在他者印象的镜子中再次折射出自我的形象，从而使客我身份得到确证。

由图4可知：随着宽跨比的增大，无论底板还是顶板剪力滞效应系数均大致呈线性增加，当宽跨比由0.2变到0.8时，顶板的剪力滞系数增加了约82.3%，底板的剪力滞系数增加了约25.1%；而当宽跨比为0.4时底板的剪力滞系数出现突变异常的原因，在于此时底板宽度基本处于“有效分布宽度”的分界点，也是剪力滞效应发挥其作用的分界点。因此，宽跨比对预应力混凝土箱梁的剪力滞效应影响很大，且顶板的剪力滞效应变化要比底板的明显。

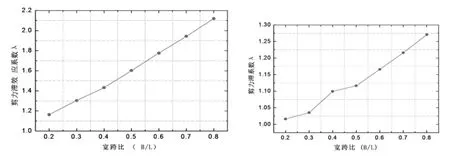
图4　不同宽跨比下箱梁跨中截面顶板、底板最大剪力滞系数变化趋势

图5　不同跨高比下箱梁跨中截面顶板、底板最大剪力滞系数变化趋势

图6　不同集中荷载大小作用下箱梁跨中截面顶板、底板最大剪力滞系数变化趋势

2.3跨高比对剪力滞系数的影响

箱梁长度为30m，考虑跨高比（L/H）分别为12、10、8、6、4，研究箱梁跨中截面最大剪力滞系数。

由图5可知：随着跨高比的增大，顶板剪力滞系数逐渐减小，底板的剪力滞系数缓慢增大。当跨高比由4增大到12时，顶板剪力滞系数减小了约27.8%，底板剪力滞系数增大了约5.1%。因此，跨高比对箱梁的剪力滞系数的影响较大，且顶板的剪力滞效应的变化要比底板的明显。

2.4集中荷载大小对剪力滞系数的影响

分别设置集中荷载大小为：10kN、15kN、20kN、25kN、30kN，保持其他结构参数不变，研究箱梁跨中截面最大剪力滞系数。

由图6可知：随着集中荷载的增大，顶板剪力滞系数逐渐增大，底板的剪力滞系数逐渐减小，但其变化的趋势越来越缓慢。当集中荷载由10kN增大到30kN时，顶板剪力滞系数增大了约2.9%，底板剪力滞系数也增大了约2.9%。故而，集中荷载的大小对箱梁的剪力滞系数的影响较小。

2.5内承托长度对剪力滞效应的影响

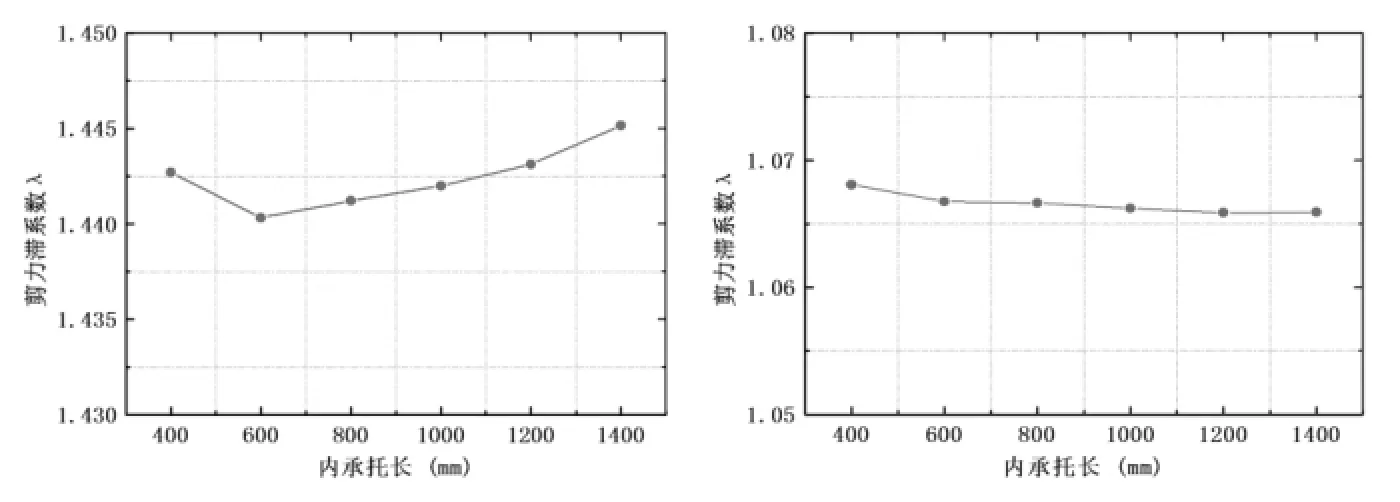
图7　不同内承托长度时箱梁跨中截面顶板、底板最大剪力滞系数变化趋势

分别设置箱梁空腔内承托尺寸为：400mm×300mm、600mm×300mm、800mm×300mm、1000mm×300mm、1200mm× 300mm、1400mm×300mm，求出各承托尺寸下顶板及底板最大剪力滞系数。

由图7可知：箱梁顶板的剪力滞系数在1.440至1.445之间，底板的剪力滞系数在1.065到1.070之间，无论顶板还是底板的剪力滞系数变化均很小，基本保持不变。因此，箱梁空腔内承托长度改变对箱梁剪力滞效应的影响可以忽略不计；同样，改变箱梁空腔外承托尺寸对箱梁剪力滞效应的影响也很小。

3　结论

以典型的预应力混凝土简支箱形梁为基础，基于ANSYS有限元软件及建立的精细化有限元分析模型，分析了预应力大小、宽跨比、跨高比、集中荷载大小及内承托长度等结构参数对箱梁剪力滞效应的影响；通过分析，可以得出以下几点结论：

⑴预应力在一定程度上可以减小顶板剪力滞效应，加大底板剪力滞效应；且对底板的剪力滞效应影响要比顶板更明显。

⑵宽跨比对箱梁剪力滞效应的影响最大；随着宽跨比的增大，无论底板还是顶板剪力滞系数均大致呈线性增加，且顶板的剪力滞效应变化要比底板的更加明显。

⑶随着跨高比的增大，顶板剪力滞系数减小，底板剪力滞系数缓慢增大，且顶板的剪力滞系数变化要比底板的明显。

⑷集中荷载大小与箱梁空腔内承托长度的变化箱梁剪力滞效应有一定的影响，但影响不大。●

［1］项海帆.高等桥梁结构理论 ［M］.北京：人民交通出版社，2001.

［2］骆佐龙，宋一凡，贺拴海，等.薄壁箱梁剪力滞效应分析的组合单元法［J］.公路交通科技，2014（09）：58-63.

［3］刘扬.薄壁箱梁剪力滞效应的研究 ［D］.重庆交通大学，2013.

［4］张伟.行车荷载作用下混凝土曲线箱梁剪力滞效应研究［D］.武汉工程大学，2014.

［5］舒志云.波形钢腹板PC组合箱梁剪力滞效应［D］.重庆交通大学，2013.

［6］陈鸿鸣，乔静宇.混凝土箱梁桥剪力滞研究现状与发展［J］.结构工程师，2011（01）：161-166.

［7］雷拓，钱江，刘成清.基于精细有限元分析的既有RC框架结构破坏机理 ［J］.中南大学学报 （自然科学版），2014（01）：214-222.

［8］刘小燕，欧阳华，沈炼.波纹钢腹板组合箱梁桥有限元精细化建模方法研究［J］.钢结构，2013（06）：1-4.

［9］HuangWX，TanLY，YangHY，etal.Discussionon CurvePrestressedReinforcementSimulationinFEA［J］. AppliedMechanicsandMaterials.2012，178-181（2012）：2179-2182.

［10］HuangWX，TanLY.NewsimulationmethodofreinforcementsimulationinFEA［J］.AppliedMechanicsand Materials，2013，405-408（2013）：972-975.

［11］黄文雄，谭利英.结构与材料参数变化对折线配筋先张梁局部应力的影响［J］.公路交通科技，2012，29（1）：75-79.

［12］黄文雄，谭利英.混凝土结构有限元分析中预应力筋模拟的新思考［J］.中外公路，2013，33（02）：108-111.

大学生创新创业训练计划项目（104892014002）