基于改进的果蝇优化算法的WSN节点部署设计
姚勇涛, 吴 雪, 吴 喆
(华东理工大学信息科学与工程学院,上海 200237)
基于改进的果蝇优化算法的WSN节点部署设计
姚勇涛,吴雪,吴喆
(华东理工大学信息科学与工程学院,上海 200237)
针对非均匀监测点的节点部署问题,设计并实现了一种简单、实用的果蝇优化算法(WSN-IFOA),构造了适用于节点部署的味道浓度函数。利用果蝇群体的随机寻优性,能够保证部署尽可能少的传感器节点使网络覆盖和连通。实验结果表明该算法在部署效果上优于基本蚁群算法,并证明了算法的可行性和有效性。
节点部署; 无线传感器网络; 果蝇优化算法; 覆盖; 连通
无线传感器网络(WSN)[1]是一种新兴的智能化网络系统,节点部署设计是WSN的关键技术,而优化的节点部署不仅需要考虑网络的覆盖,还要考虑网络的连通性。目前的覆盖技术主要包括区域覆盖、点覆盖、栅栏覆盖3种。
本文的研究背景是基于区域的点覆盖。网络连通则要求整个工作的区域网络是一个整体,不能够被分割,也就是要求每个部署的传感器节点通过单跳或者多跳都必须连接到sink点。优化部署的目的就是要求部署尽可能少的传感器节点使网络覆盖和连通。
如今,智能优化算法[2-3]被越来越多地应用于无线传感器网络。智能优化算法包括遗传算法、模拟退火算法、鱼群算法、蚁群算法等。文献[4]提出了在障碍物干扰下的遗传算法,但是没有考虑sink点的位置对于节点部署的影响。文献[5]提出了基于模拟退火算法的节点部署方法,但没有考虑部署节点之间的连通性。文献[6]提出了基于粒子群的节点部署,它将能耗与覆盖率同时考虑,但能量对于节点的移动性有很大影响。针对这些算法存在的连通问题和sink点位置问题,本文提出了一种新的简单、高效的智能算法——果蝇算法。针对无线传感器网络非均匀监测点的节点部署问题,以网格点为背景随机地构造监测点,并针对WSN自身特点设计出果蝇算法的气味函数模型,将覆盖与连通同时考虑,该算法既能保证高效性又能有效部署较少的传感器节点。将本文提出的算法与蚁群算法对无线传感器网络的节点部署设计进行了对比,实验结果验证了本文算法的可行性。
1 网格部署基本概念
本文基于网格为背景的模型对节点部署进行建模[7-8]。图1所示为监测点集和有效点集示意图。图中的监测点为不均匀分布的需要被传感器节点覆盖的点(用◇和□表示); 传感器节点是部署设计的点,目的是将监测点完全覆盖(用■表示); 候选网格点为以sink点和已经部署的传感器节点为圆心,以通信半径为半径画圆,圆形区域面积的并集区域里的网格点; 有效点为候选网格区域中能够覆盖未被覆盖的监测点的网格点(用○表示)。
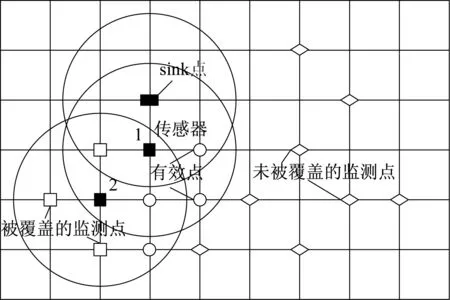
图1 监测点集和有效点集Fig.1 Monitoring and effective nodes collection
在网格背景模型下,所有的点,无论是监测点还是需要部署的传感器节点都属于网格点。本文的背景是基于区域的点覆盖,即在网格上随机产生不均匀的监测点,部署尽可能少的传感器节点去完全覆盖这些监测点,并保证所有监测点和sink点的连通性。
在构建的网格点上,首先随机产生不均匀分布的监测点集,固定sink点在网格上的位置,并确定sink点和待部署的传感器节点的通信半径。本文中节点通信半径和传感器半径相等。在sink节点的通信半径内,首先按照一定的规则选择网格点1作为第1个被部署的传感器节点,再以sink点和传感器节点1所组成的候选网格点内继续按照一定规则选择传感器节点2,如此反复,直到完成需要规划的目标(即覆盖所有的监测点并使它们全部直接或间接连通到sink点)为止。
2 基本果蝇算法
果蝇优化算法(FOA)[9-10]是一种基于果蝇觅食行为推演出寻求全局优化的新方法,被应用于金融预警模式之中。果蝇本身在感官直觉上优于其他物种,尤其在视觉与嗅觉上,果蝇的嗅觉可以搜索甚至40 km以外的食物源,当发现离食物的位置更近后,可以利用视觉发现果蝇群聚集的位置,并往该位置飞去。图2示出了基本果蝇寻优模型示意图,算法步骤如下:
(1) 随机初始化果蝇群体位置initX0,initY0。
(2) 赋予果蝇个体利用嗅觉搜寻食物之随机方向与距离如式(1)、式(2)所示。
(1)
(2)
(3) 由于无法得知食物位置,因此先估计与原点之距离di,再计算味道浓度判定值si。
(3)
(4)
(4) 将味道浓度判定值si代入味道浓度判定函数,求出该果蝇个体位置的味道浓度,如式(5)。
smell(i)=f(si)
(5)
找出此果蝇群体中味道浓度最高的果蝇(求极大值),如式(6)。
bestsmell=max(smell(i))
(6)
(5) 保留最佳味道浓度值与坐标,此时果蝇群体利用视觉往该位置飞去,进入迭代寻优并判断味道浓度是否优于前一迭代味道浓度,若是,则果蝇群体飞往新位置,如此反复,直到达到需要规划的目标为止。
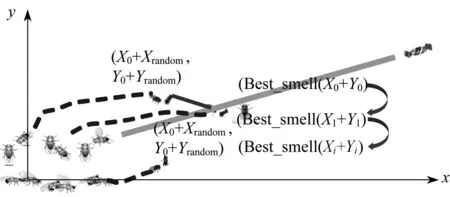
图2 基本果蝇寻优模型示意图Fig.2 Scheme of basic FOA model
3 WSN-IFOA算法的节点部署设计
本文以网格为WSN背景模型建模,对果蝇算法的气味函数进行改进,使其应用于无线传感器网络的非均匀点监测的节点部署,在保证整个网络覆盖和连通的前提下,设计能够高效部署节点的优化算法。
设传感器节点的通信半径为rs,监测点(x′,y′)与传感器节点(xi,yi)的距离为D(i),则
(7)
当D(i)≤rs时,监测点(x′,y′)可以被传感器节点(xi,yi)覆盖。
在果蝇算法中,果蝇群体中的每一个个体会根据自身所处的位置与初始位置的关系,计算出它们各自的味道浓度判定函数值,得到最佳的味道浓度,从而确定下一步的位置。基本的果蝇算法味道浓度判定值是基于距离的,本文考虑的是基于区域的点覆盖,在WSN-IFOA中,通过计算动态的候选网格点集合中果蝇随机选择的各个网格点的味道浓度判定函数值的最大值作为下一个部署的传感器节点。味道浓度由以下两部分因素组成:
(8)
(9)

smell(vi)=w1f1+w2(1-f2)
(10)
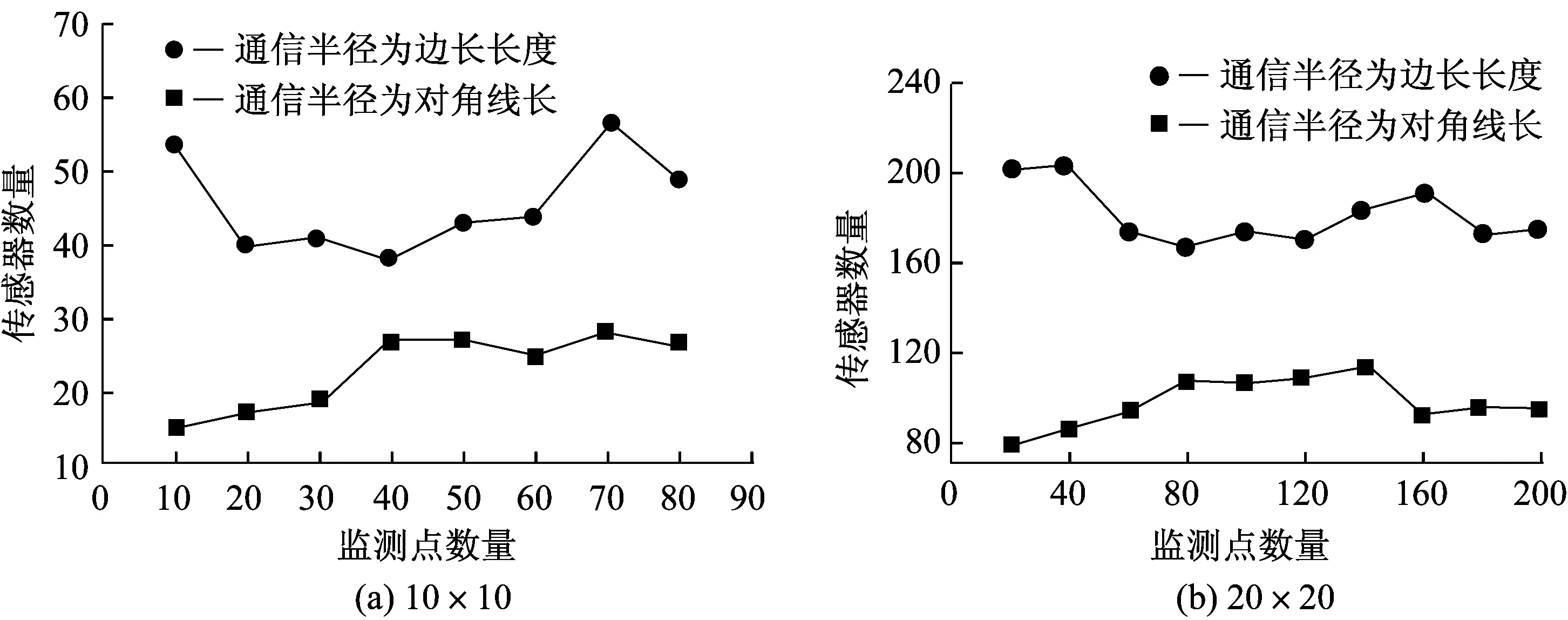
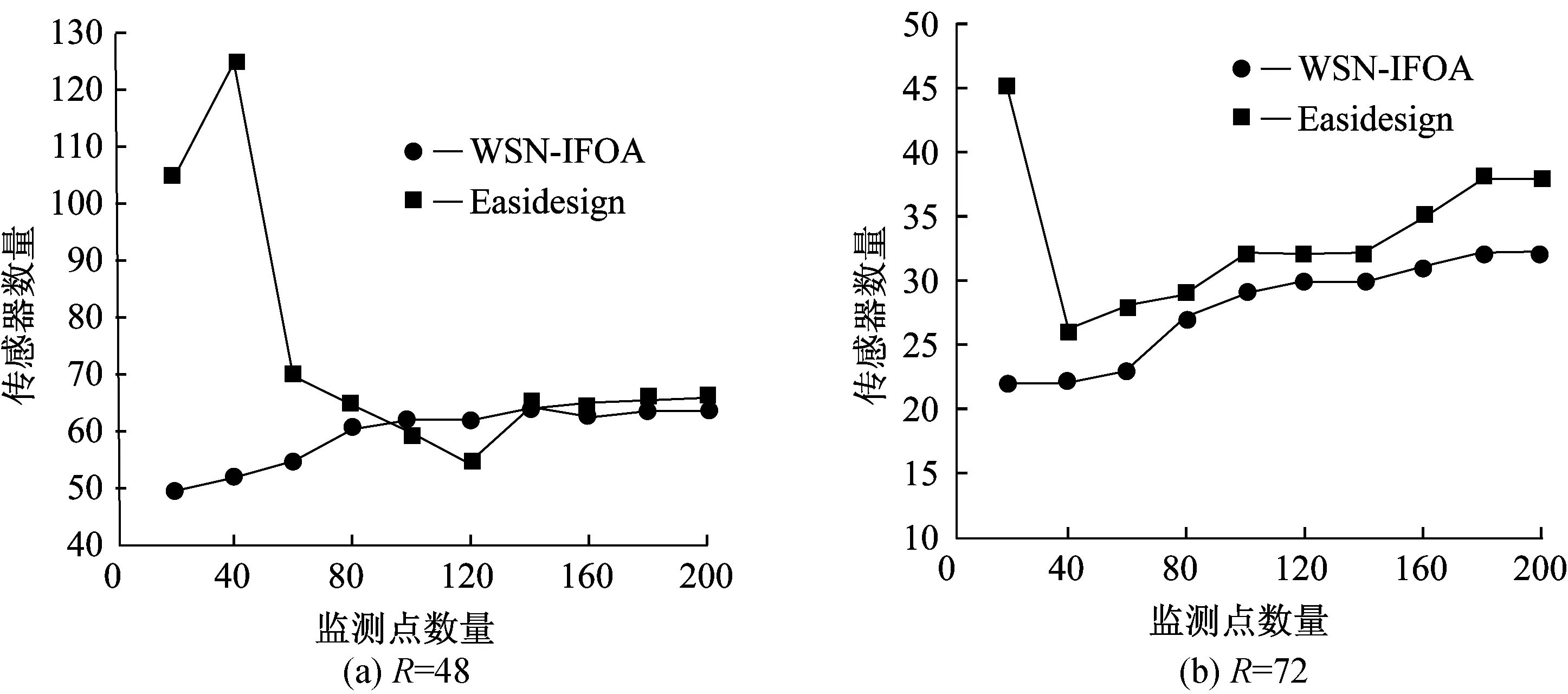
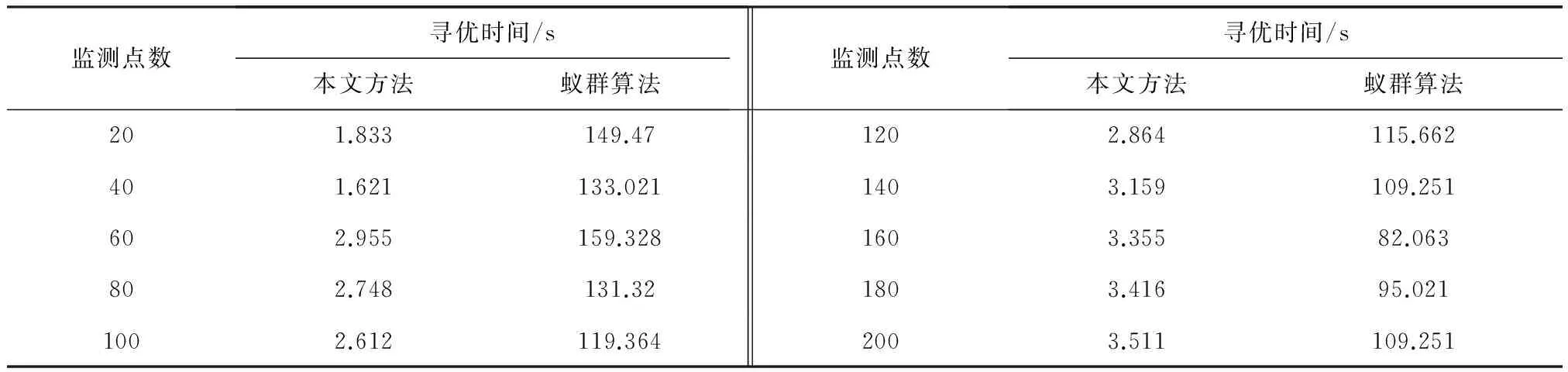
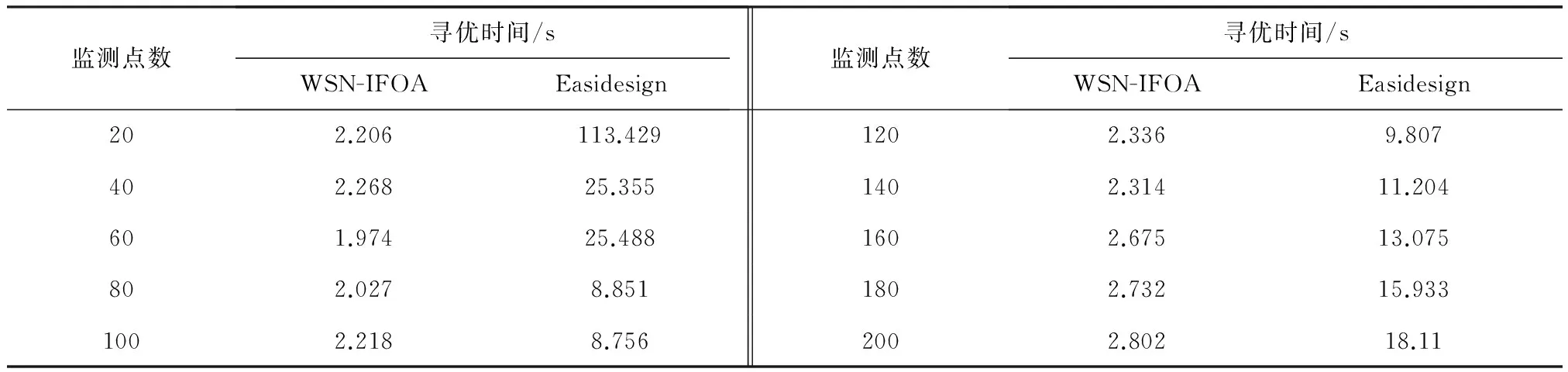
其中:w1和w2表示权重,0 将式(8)、式(9)代入式(10),得 (11) 将WSN-IFOA算法应用于无线传感器网络的非均匀监测点的节点部署设计中,算法步骤如下: (1) 固定sink点的位置,将果蝇群体的初始位置放于sink节点的通信半径内。 (2) 赋予每个果蝇个体在候选网格点集合范围内,随机的方向和距离。 (3) 计算各个目标网格点覆盖的监测点个数,进一步计算得到各个点的味道浓度判定值。 (4) 将味道浓度判定值带入气味函数,如式(11),计算出下一跳味道浓度判定函数最大的目标网格点,记下该位置,果蝇群体飞向该位置。 (5) 利用贪婪法循环迭代此步骤,判断味道浓度是否优于前一次的味道浓度,若不是,则返回上一跳节点。 (6) 直到所有的监测点被完全覆盖,则算法结束。 WSN-IFOA算法流程图如图3所示。 图3 WSN-IFOA算法流程图Fig.3 Flow chat of WSN-IFOA algorithm 4.1不同的通信半径对算法的影响 图4示出了不同的通信半径对节点部署的影响。其中图4(a)设定网格点规模为10×10,图4(b)设定网格点规模为20×20,网格边长均为24。 如图4所示,无论网格规模大小,当通信半径等于网格对角线长时,实验结果比通信半径等于网格边长时的效果要好得多。在后期的实验中也证明,通信半径必须大于网格的对角线长,才会表现出比较好的效果。因为从理论分析上讲,所部署的传感器节点必须是在网格点集中选取的,所以通信半径等于甚至小于网格边长的话,则可以选取的网格点就会很少,算法将会受到很大制约。 4.2不同的网格规模对算法的影响 图5示出了不同的网格规模对节点部署的影响。 图4 不同的通信半径对于节点部署的影响Fig.4 Influence of different communication radii for node deployment 图5 不同的网格规模对节点部署的影响Fig.5 Influence of different mesh dimensions for node deployment 图5(a)设定网格规模为9×9,网格边长为24,传感器节点的通信半径为24; 图5(b)设定网格点规模为9×9,网格边长为24,传感器节点的通信半径为48; 图5(c)设定网格点规模为17×17,网格边长为12,传感器节点的通信半径为48; 图5(d)设定网格点规模为33×33,网格边长为6,传感器节点的通信半径为48。图中实心点表示不均匀分布的监测点集,监测点个数均为60个,并且相对位置相同。空心点代表部署的传感器节点。 由图5可以看出,图5(a)部署的传感器节点数为31,图5(b)为17,图5(c)为14,图6(d)为15。比较图5(a)和图5(b)可知,在网格规模和监测点相同的情况下,传感器节点的通信半径越大,则部署的传感器节点越少。比较图5(b)、5(c)、5(d)可知,传感器节点的通信半径相等,在监测点相对位置相同的情况下,并不是网格规模越大,所需要部署的传感器节点越少。当网格规模增加到一定程度后,所部署的传感器节点数基本变化不大。 4.3sink点位置不同对算法的影响 图6示出了sink点位置不同对节点部署的影响。图6中网格点的规模为20×20,网格的边长为24。图6(a)中传感器节点的通信半径为48,图6(b)中传感器节点的通信半径为72。将sink点分别固定在区域的中心和边缘进行比较。 图6 sink点位置不同对节点部署的影响Fig.6 Influence of different sink node position for node deployment 由图6可以看出,sink点固定在区域中心相对于固定在区域边缘所需要部署的传感器节点的浮动变化曲线较为平滑,但是传感器节点数量的最大值与最小值的差值区间较大。如图6(a)中,当sink点固定在区域边缘时传感器节点数量的最大值为63,即当监测点为20时所部署的传感器节点数量的最小值为51,差值为12; 当sink点固定在区域中心时差值为24。传感器节点的通信半径越大,则部署传感器节点的个数越少,而且差值区间的变化也相对比较小。 4.4果蝇种群的数量对算法的影响 图7示出了果蝇种群的数量对节点部署的影响。图7中网格点的规模为20×20,网格的边长为24。图7(a)中传感器节点的通信半径为48,图7(b)中传感器节点的通信半径为72,sink点均固定在网格点的中心。在均将果蝇的初始位置置于sink点的通信半径内的条件下,分别取果蝇种群为50和100进行比较。 图7 果蝇种群数量对于节点部署的影响Fig.7 Influence of fruit fly population for node deployment 由图7可以看出,果蝇种群数量为100的果蝇群平均所用的传感器节点数少于果蝇种群为50的果蝇群。但是果蝇种群数量等于50时,比数量等于100时的果蝇群相对所部署的传感器节点数量的波动要小,即曲线相对稳定。当监测点达到一定数量时,部署的传感器节点变动的幅度不大。传感器节点的通信半径越大,则部署传感器节点的个数越少。 4.5寻优性能比较 设定网格的规模为20×20,网格的边长为24,传感器节点的通信半径分别为48和72,sink点固定在网格的中心,果蝇种群的数量为40。图8示出了WSN-IFOA算法和基本蚁群算法(Easidesign)寻优性能的比较结果。 由图8可以看出,监测点数目不同,部署的传感器节点数目也不同。在两种通信半径条件下,WSN-IFOA算法的稳定性明显比Easidesign算法好,平均所部署的传感器节点数也要少。尤其在监测点稀疏的条件下,Easidesign算法很不稳定,并且没有得到比较好的解。当监测点比较多时,两者的差距较小。在效率上,WSN-IFOA算法比传统方法节省更多的CPU计算时间,比较结果见表1、表2。由此可以看出,本文算法的复杂度更低。总之,无论是在监测点多还是少的情况下,本文算法都能够保证能够找到比较好的传感器节点解集。 图8 WSN-IFOA与Easidesign的寻优性能比较Fig.8 Comparison of WSN-IFOA and Easidesign optimization 表1 R=48时完成寻优所需时间 Table 1 CPU times of the optimization (R=48) 监测点数寻优时间/s本文方法蚁群算法监测点数寻优时间/s本文方法蚁群算法201.833149.471202.864115.662401.621133.0211403.159109.251602.955159.3281603.35582.063802.748131.321803.41695.0211002.612119.3642003.511109.251 表2 R=72时完成寻优所需时间 本文提出了一种基于改进果蝇优化的算法(WSN-IFOA)用于节点的部署设计,该算法构建了适用于节点部署的气味函数模型,可以有效地在随机产生的不同数量的监测点集的情况下进行传感器节点的部署设计。实验结果表明了不同网格规模和不同果蝇种群数量对于该算法的影响。在与传统蚁群算法的比较中可以看出,在相同规模网格点的情况下,无论是在监测点多还是少的情况下,该算法均表现出比较好的部署效果。 [1]CURIAC DANIEL-IOAN.A survey on redundancy and its applications in wireless sensor networks[J].WSEAS Transactions on Computers,2009,8(4):705-714. [2]CORMEN T H,CHARLES E L,RONALD L R,etal.Introduction to Algorithms[M].Second Edition.Massachusetts:The MIT Press,2001. [3]WEI L,LI C.Ant based approach to the optimal deployment in wireless sensor networks[J].Journal on Communications,2009,30:25-33. [4]JOURDAN D B,DE WECK O L.Layout optimization for a wireless sensor network using a multi-objective genetic algorithm[C]//2004 IEEE 59th Vehicular Technology Conference.USA:IEEE,2004:2466-2470. [5]LIN F,CHIU P L.A near-optimal sensor placement algorithm to achieve complete coverage-discrimination in sensor networks[J].IEEE Communications Letters,2005,9(1):43-45. [6]AZIZ N A A,MOHEMMED A W,ZHANG M.Particle swarm optimization for coverage maximization and energy conservation in wireless sensor networks[C]//Applications of Evolutionary Computation.UK:Springer Berlin Heidelberg,2010:51-60. [7]KHAN S U.Approximate optimal sensor placements in grid sensor fields[C]//2007 IEEE 65th Vehicular Technology Conference.USA:IEEE,2007:248-251. [8]JOURDAN D B,DE WECK O L.Layout optimization for a wireless sensor network using a multi-objective genetic algorithm[C]//2004 IEEE 59th Vehicular Technology Conference.USA:IEEE,2004:2466-2470. [9]PAN W T.A new fruit fly optimization algorithm:Taking the financial distress model as an example[J].Knowledge-Based Systems,2012,26:69-74. [10]HAN Junying,LIU Chengzhong.Fruit fly optimization algorithm with adaptive mutation[J].Application Research of Computers,2013,30(9):2641-2644. Wireless Sensor Network Node Deployment Design Based on Improved Fruit Fly Optimization Algorithm YAO Yong-tao,WU Xue,WU Zhe (School of Information Science and Engineering,East China University of Science and Technology,Shanghai 200237,China) Aiming at the problem of non-uniform monitoring node deployment,this paper proposes an improved fruit fly algorithm,WSN-IFOA,by constructing the flavor concentration function suitable for deployment of nodes.The proposed algorithm utilizes the stochastic optimization of fruit fly group to ensure the coverage and communication of network by means of sensor node as few as possible.It is shown from experiment results that the proposed algorithm is superior to the classical ant colony algorithm and is feasible and effective. node deployment; wireless sensor network; fruit fly optimization algorithm; coverage; connection 1006-3080(2016)04-0545-07 10.14135/j.cnki.1006-3080.2016.04.016 2015-10-30 姚勇涛(1989-),女,安徽合肥人,硕士生,研究方向为无线传感器网络。E-mail:947096217@qq.com 通信联系人:吴 雪,E-mail:wuxue@ecust.edu.cn TP391 A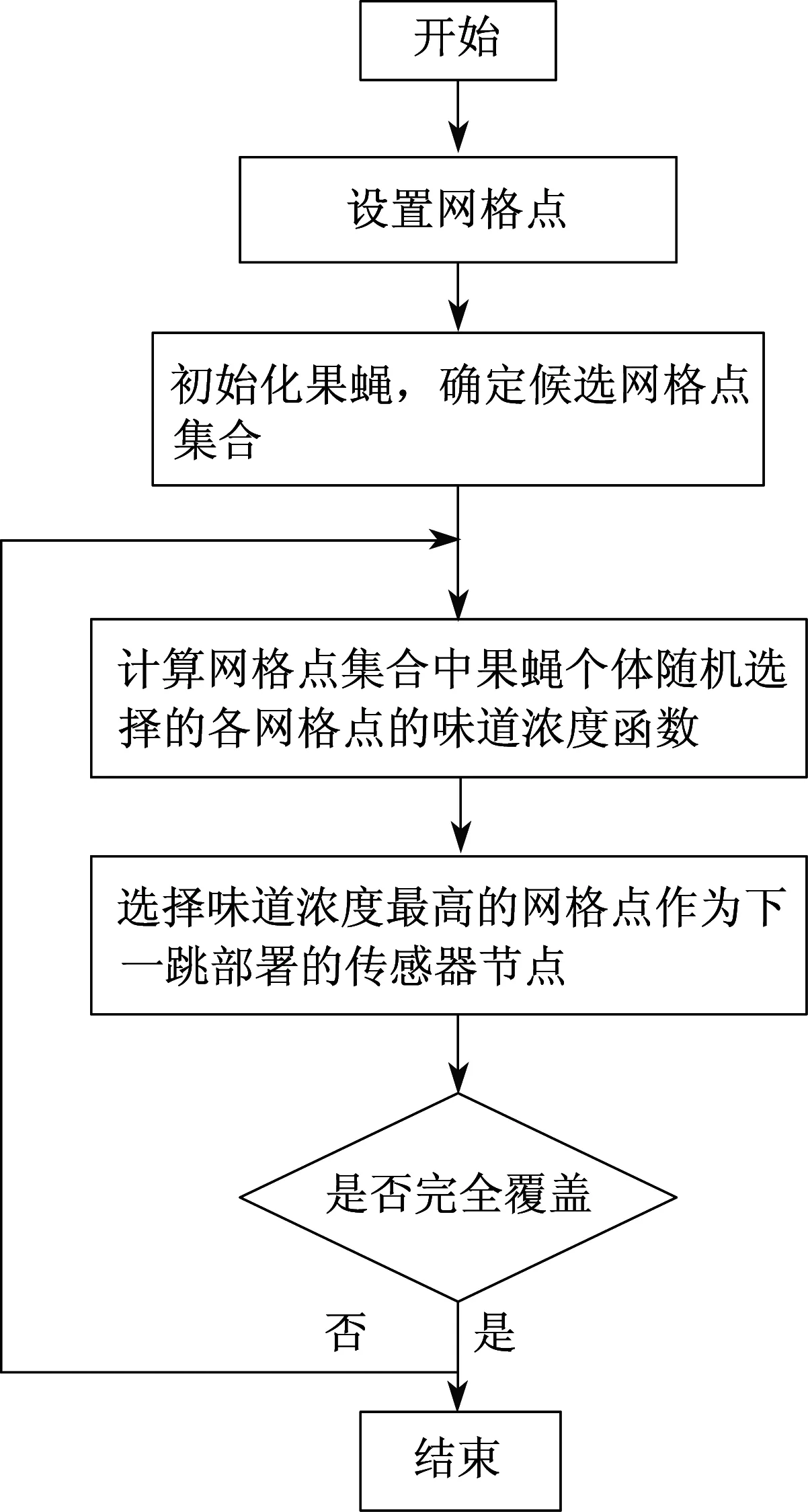
4 仿真实验



5 结 论

